Más sobre forecasting en cienciadedatos.net
- Forecasting series temporales con machine learning
- Modelos ARIMA y SARIMAX
- Forecasting series temporales con gradient boosting: XGBoost, LightGBM y CatBoost
- Global Forecasting: Multi-series forecasting
- Forecasting de la demanda eléctrica con machine learning
- Forecasting con deep learning
- Forecasting de visitas a página web con machine learning
- Forecasting del precio de Bitcoin
- Forecasting probabilístico
- Forecasting de demanda intermitente
- Reducir el impacto del Covid en modelos de forecasting
- Modelar series temporales con tendencia utilizando modelos de árboles

Introducción¶
Deep Learning es un campo de la inteligencia artificial centrado en crear modelos basados en redes neuronales que permiten aprender representaciones no lineales. Las redes neuronales recurrentes (RNN) son un tipo de arquitectura de deep learning diseñada para trabajar con datos secuenciales, donde la información se propaga a través de conexiones recurrentes, lo que permite a la red aprender patrones temporales.
Este artículo describe cómo entrenar modelos de redes neuronales recurrentes, específicamente RNN, GRU y LSTM, para la predicción de series temporales (forecasting) utilizando Python, Keras y skforecast.
Keras3 proporciona una interfaz amigable para construir y entrenar modelos de redes neuronales. Gracias a su API de alto nivel, los desarrolladores pueden implementar fácilmente arquitecturas LSTM, aprovechando la eficiencia computacional y la escalabilidad que ofrece el deep learning.
Skforecast facilita la implementación y uso de modelos de machine learning para problemas de predicción. Con este paquete, el usuario puede definir el problema y abstraerse de la arquitectura. Para usuarios avanzados, skforecast también permite ejecutar una arquitectura de deep learning previamente definida.
✏️ Note
Para comprender plenamente este artículo, se presupone cierto conocimiento sobre redes neuronales y deep learning. No obstante, si este no es el caso, y mientras trabajamos en la creación de nuevo material, te proporcionamos algunos enlaces de referencia para comenzar:
Redes Neuronales Recurrentes (RNN)¶
Las Redes Neuronales Recurrentes (RNN) son una familia de modelos específicamente diseñados para trabajar con datos secuenciales, como las series temporales. A diferencia de las redes neuronales tradicionales (feedforward), que tratan cada entrada de forma independiente, las RNN incorporan una memoria interna que les permite capturar dependencias entre los elementos de una secuencia. Esto permite al modelo aprovechar la información de los pasos previos para mejorar las predicciones futuras.
El bloque fundamental de una RNN es la célula recurrente, que en cada paso temporal recibe dos entradas: el dato actual y el estado oculto anterior (la "memoria" de la red). En cada iteración, el estado oculto se actualiza almacenando la información relevante de la secuencia hasta ese momento. Esta arquitectura permite que las RNN puedan “recordar” tendencias y patrones a lo largo del tiempo.
Sin embargo, las RNN simples tienen dificultades para aprender dependencias a largo plazo debido a problemas como el desvanecimiento o explosión del gradiente. Para superar estas limitaciones, se desarrollaron arquitecturas más avanzadas como las Long Short-Term Memory (LSTM) y las Gated Recurrent Unit (GRU). Estas variantes son más eficaces capturando patrones complejos y de largo alcance en datos de series temporales.
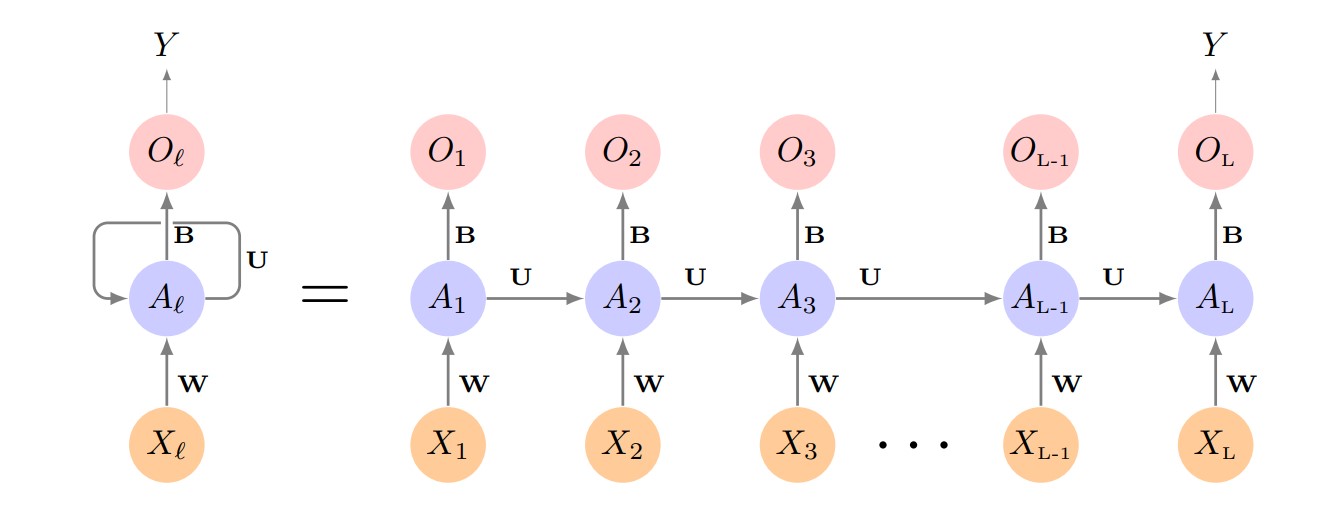
Diagrama de una red RNN simple. Fuente: James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An introduction to statistical learning (1st ed.) [PDF]. Springer.
Long Short-Term Memory (LSTM)¶
Las Long Short-Term Memory (LSTM) son un tipo de red neuronal recurrente ampliamente utilizada, diseñada para capturar de forma efectiva dependencias a largo plazo en datos secuenciales. A diferencia de las RNN simples, las LSTM emplean una arquitectura más sofisticada basada en un sistema de celdas de memoria y compuertas (gates) que controlan el flujo de información a lo largo del tiempo.
El componente central de una LSTM es la celda de memoria, que mantiene la información a través de los distintos pasos temporales. Tres compuertas regulan cómo se añade, retiene o descarta la información en cada iteración:
Forget Gate (Compuerta de Olvido): Decide qué información del estado previo de la celda debe eliminarse. Utiliza la entrada actual y el estado oculto anterior, aplicando una activación sigmoide para obtener un valor entre 0 y 1 (donde 0 significa “olvidar completamente” y 1 significa “conservar completamente”).
Input Gate (Compuerta de Entrada): Controla cuánta información nueva se añade al estado de la celda, también usando la entrada actual y el estado oculto previo con una activación sigmoide.
Output Gate (Compuerta de Salida): Determina cuánta información del estado de la celda se muestra como salida y se transmite al siguiente estado oculto.
Este mecanismo de compuertas permite a las LSTM recordar o “olvidar” información de manera selectiva, lo que las hace especialmente eficaces para modelar secuencias con patrones de largo plazo.
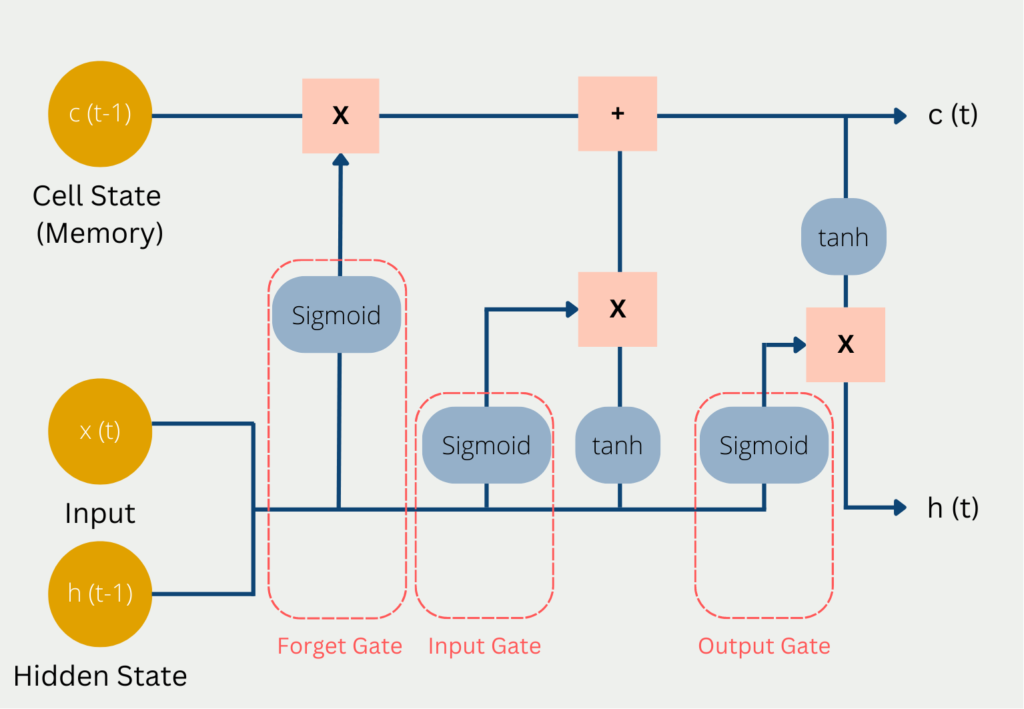
Diagrama de entradas y salidas de una LSTM. Fuente: codificandobits https://databasecamp.de/wp-content/uploads/lstm-architecture-1024x709.png.
Las Gated Recurrent Unit (GRU) son una alternativa simplificada a las LSTM, ya que utilizan solo dos compuertas (reset y update), pero suelen alcanzar un rendimiento similar. Las GRU requieren menos parámetros y pueden ser computacionalmente más eficientes, lo que puede suponer una ventaja en ciertas tareas o cuando se trabaja con conjuntos de datos de gran tamaño.
Tipos de capas recurrentes en skforecast¶
Con skforecast, puedes utilizar tres tipos de células recurrentes:
Simple RNN: Adecuada para problemas con dependencias de corto plazo o cuando un modelo sencillo es suficiente. Es menos eficaz capturando patrones a largo plazo.
LSTM (Long Short-Term Memory): Incorpora mecanismos de compuertas que permiten a la red aprender y retener información durante periodos más largos. Las LSTM son una opción popular para muchos problemas de predicción complejos.
GRU (Gated Recurrent Unit): Ofrece una estructura más simple que la LSTM, utilizando menos parámetros y logrando un rendimiento comparable en muchos escenarios. Resulta útil cuando la eficiencia computacional es importante.
✏️ Note
Recomendaciones para elegir una capa recurrente:
- Utiliza LSTM si tu serie temporal presenta patrones a largo plazo o dependencias complejas.
- Prueba con GRU como alternativa más ligera a LSTM.
- Emplea Simple RNN solo en tareas sencillas o como modelo de referencia.
Tipos de problemas en forecasting¶
La complejidad de un problema de predicción en series temporales suele estar determinada por tres preguntas clave:
¿Qué series se van a utilizar para entrenar el modelo?
¿Qué series (y cuántas) se quieren predecir?
¿Cuántos pasos hacia el futuro se desean predecir?
Estas decisiones condicionan la estructura de tu conjunto de datos y el diseño del modelo de predicción, y son esenciales a la hora de abordar problemas de series temporales.
Los modelos de deep learning para series temporales pueden abordar una gran variedad de escenarios de predicción, todo depende de cómo se estructuren los datos de entrada y qué objetivos de predicción se definan. Estos modelos pueden modelar los siguientes escenarios:
Problemas 1:1 — Serie única, salida única
- Descripción: El modelo utiliza únicamente los valores pasados de una serie para predecir sus propios valores futuros. Es el enfoque clásico autorregresivo.
- Ejemplo: Predecir la temperatura de mañana usando solo las mediciones previas de temperatura.
Problemas N:1 — Multiserie, salida única
- Descripción: El modelo utiliza varias series como predictores, pero el objetivo es solo una de ellas. Cada predictor puede ser una variable o entidad diferente, pero solo se pronostica una serie de salida.
- Ejemplo: Predecir la temperatura de mañana usando la temperatura, humedad y presión atmosférica.
Problemas N:M — Multiserie, múltiples salidas
- Descripción: El modelo emplea múltiples series como predictores y pronostica varias series objetivo al mismo tiempo.
- Ejemplo: Pronosticar los valores en bolsa de varias acciones en función del histórico de la bolsa, del precio de la energía y materias primas.
Todos estos escenarios pueden plantearse tanto como single-step forecasting (predecir solo el siguiente punto temporal) o como multi-step forecasting (predecir varios puntos futuros).
Además, puedes mejorar tus modelos incorporando variables exógenas, es decir, características externas o información adicional conocida de antemano (como efectos de calendario, promociones o previsión meteorológica), junto con los datos principales de la serie temporal.
Definir la arquitectura de deep learning adecuada para cada caso puede ser todo un reto. La librería skforecast ayuda seleccionando automáticamente la arquitectura idónea en cada escenario, lo que facilita y acelera el proceso de modelado.
A continuación, encontrarás ejemplos de cómo usar skforecast para resolver cada uno de estos problemas de series temporales utilizando redes neuronales recurrentes.
Datos¶
Los datos empleados en este artículo contienen información detallada sobre la calidad del aire en la ciudad de Valencia (España). La colección de datos abarca desde el 1 de enero de 2019 hasta el 31 de diciembre de 2021, proporcionando mediciones horarias de diversos contaminantes atmosféricos, como partículas PM2.5 y PM10, monóxido de carbono (CO), dióxido de nitrógeno (NO2), entre otros. Los datos se han obtenido de plataforma *Red de Vigilancia y Control de la Contaminación Atmosférica, 46250054-València - Centre, https://mediambient.gva.es/es/web/calidad-ambiental/datos-historicos.
Librerías¶
⚠️ Warning
skforecast es compatible con varios backends de Keras: TensorFlow, JAX y PyTorch (torch). Puedes seleccionar el backend utilizando la variable de entorno KERAS_BACKEND o editando tu archivo de configuración local en ~/.keras/keras.json.
```python
import os
os.environ["KERAS_BACKEND"] = "torch" # Opciones: "tensorflow", "jax", o "torch"
import keras
```
El backend debe configurarse antes de importar Keras en tu sesión de Python. Una vez que Keras ha sido importado, el backend no puede cambiarse sin reiniciar el entorno.
Como alternativa, puedes definir el backend en el archivo de configuración en ~/.keras/keras.json:
```json
{
"backend": "torch" # Opciones: "tensorflow", "jax", o "torch"
}
```
# Procesado de datos
# ==============================================================================
import os
import numpy as np
import pandas as pd
# Gráficos
# ==============================================================================
import matplotlib.pyplot as plt
import plotly.graph_objects as go
import plotly.io as pio
import plotly.offline as poff
pio.templates.default = "seaborn"
poff.init_notebook_mode(connected=True)
# Keras
# ==============================================================================
os.environ["KERAS_BACKEND"] = "torch" # 'tensorflow', 'jax´ or 'torch'
import keras
from keras.optimizers import Adam
from keras.losses import MeanSquaredError
from keras.callbacks import EarlyStopping, ReduceLROnPlateau
# Feature engineering
# ==============================================================================
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import make_pipeline
from feature_engine.datetime import DatetimeFeatures
from feature_engine.creation import CyclicalFeatures
# Modelado
# ==============================================================================
import skforecast
from skforecast.plot import set_dark_theme
from skforecast.datasets import fetch_dataset
from skforecast.deep_learning import ForecasterRnn
from skforecast.deep_learning import create_and_compile_model
from skforecast.model_selection import TimeSeriesFold
from skforecast.model_selection import backtesting_forecaster_multiseries
from skforecast.plot import plot_prediction_intervals
# Configuración warnings
# ==============================================================================
import warnings
warnings.filterwarnings('ignore', category=DeprecationWarning)
color = '\033[1m\033[38;5;208m'
print(f"{color}skforecast version: {skforecast.__version__}")
print(f"{color}Keras version: {keras.__version__}")
print(f"{color}Using backend: {keras.backend.backend()}")
if keras.backend.backend() == "tensorflow":
import tensorflow as tf
print(f"{color}tensorflow version: {tf.__version__}")
elif keras.backend.backend() == "torch":
import torch
print(f"{color}torch version: {torch.__version__}")
print(" Cuda available :", torch.cuda.is_available())
print(" Device name :", torch.cuda.get_device_name(0) if torch.cuda.is_available() else "CPU")
else:
print(f"{color}Backend not recognized. Please use 'tensorflow' or 'torch'.")
skforecast version: 0.19.0 Keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126 Cuda available : True Device name : Tesla T4
# Descarga y procesado de datos
# ==============================================================================
data = fetch_dataset(name="air_quality_valencia_no_missing")
data.head()
╭──────────────────────── air_quality_valencia_no_missing ─────────────────────────╮ │ Description: │ │ Hourly measures of several air chemical pollutant at Valencia city (Avd. │ │ Francia) from 2019-01-01 to 20213-12-31. Including the following variables: │ │ pm2.5 (µg/m³), CO (mg/m³), NO (µg/m³), NO2 (µg/m³), PM10 (µg/m³), NOx (µg/m³), │ │ O3 (µg/m³), Veloc. (m/s), Direc. (degrees), SO2 (µg/m³). Missing values have │ │ been imputed using linear interpolation. │ │ │ │ Source: │ │ Red de Vigilancia y Control de la Contaminación Atmosférica, 46250047-València - │ │ Av. França, https://mediambient.gva.es/es/web/calidad-ambiental/datos- │ │ historicos. │ │ │ │ URL: │ │ https://raw.githubusercontent.com/skforecast/skforecast- │ │ datasets/main/data/air_quality_valencia_no_missing.csv │ │ │ │ Shape: 43824 rows x 10 columns │ ╰──────────────────────────────────────────────────────────────────────────────────╯
| so2 | co | no | no2 | pm10 | nox | o3 | veloc. | direc. | pm2.5 | |
|---|---|---|---|---|---|---|---|---|---|---|
| datetime | ||||||||||
| 2019-01-01 00:00:00 | 8.0 | 0.2 | 3.0 | 36.0 | 22.0 | 40.0 | 16.0 | 0.5 | 262.0 | 19.0 |
| 2019-01-01 01:00:00 | 8.0 | 0.1 | 2.0 | 40.0 | 32.0 | 44.0 | 6.0 | 0.6 | 248.0 | 26.0 |
| 2019-01-01 02:00:00 | 8.0 | 0.1 | 11.0 | 42.0 | 36.0 | 58.0 | 3.0 | 0.3 | 224.0 | 31.0 |
| 2019-01-01 03:00:00 | 10.0 | 0.1 | 15.0 | 41.0 | 35.0 | 63.0 | 3.0 | 0.2 | 220.0 | 30.0 |
| 2019-01-01 04:00:00 | 11.0 | 0.1 | 16.0 | 39.0 | 36.0 | 63.0 | 3.0 | 0.4 | 221.0 | 30.0 |
Se verifica que el conjunto de datos tiene un índice de tipo DatetimeIndex con frecuencia horaria.
# Comprobación de índice y frecuencia
# ==============================================================================
print(f"Tipo de índice : {data.index.dtype}")
print(f"Frecuencia : {data.index.freq}")
Tipo de índice : datetime64[ns] Frecuencia : <Hour>
Para facilitar el entrenamiento de los modelos y la evaluación de su capacidad predictiva, los datos se dividen en tres conjuntos separados: entrenamiento, validación y test.
# Split train-validation-test
# ==============================================================================
data = data.loc["2019-01-01 00:00:00":"2021-12-31 23:59:59", :].copy()
end_train = "2021-03-31 23:59:00"
end_validation = "2021-09-30 23:59:00"
data_train = data.loc[:end_train, :].copy()
data_val = data.loc[end_train:end_validation, :].copy()
data_test = data.loc[end_validation:, :].copy()
print(
f"Fechas train : {data_train.index.min()} --- "
f"{data_train.index.max()} (n={len(data_train)})"
)
print(
f"Fechas validation : {data_val.index.min()} --- "
f"{data_val.index.max()} (n={len(data_val)})"
)
print(
f"Fechas test : {data_test.index.min()} --- "
f"{data_test.index.max()} (n={len(data_test)})"
)
Fechas train : 2019-01-01 00:00:00 --- 2021-03-31 23:00:00 (n=19704) Fechas validation : 2021-04-01 00:00:00 --- 2021-09-30 23:00:00 (n=4392) Fechas test : 2021-10-01 00:00:00 --- 2021-12-31 23:00:00 (n=2208)
# Plot series
# ==============================================================================
set_dark_theme()
colors = plt.rcParams['axes.prop_cycle'].by_key()['color'] * 2
fig, axes = plt.subplots(len(data.columns), 1, figsize=(8, 8), sharex=True)
for i, col in enumerate(data.columns):
axes[i].plot(data[col], label=col, color=colors[i])
axes[i].legend(loc='upper right', fontsize=8)
axes[i].tick_params(axis='both', labelsize=8)
axes[i].axvline(pd.to_datetime(end_train), color='white', linestyle='--', linewidth=1) # End train
axes[i].axvline(pd.to_datetime(end_validation), color='white', linestyle='--', linewidth=1) # End validation
fig.suptitle("Air Quality Valencia", fontsize=16)
plt.tight_layout()
Creación sencilla de modelos basados en RNN con create_and_compile_model¶
skforecast proporciona la función create_and_compile_model para simplificar la creación de arquitecturas de redes neuronales recurrentes (RNN, LSTM o GRU) para la predicción de series temporales. Esta función está diseñada para facilitar tanto a usuarios principiantes como avanzados la construcción y compilación de modelos de Keras con solo unas pocas líneas de código.
Uso básico
Para la mayoría de los escenarios de predicción, es suficiente con especificar los datos de la serie temporal, el número de observaciones rezagadas (lags), el número de pasos a predecir y el tipo de capa recurrente que deseas utilizar (LSTM, GRU o SimpleRNN). Por defecto, la función establece parámetros razonables para cada capa, aunque todos los parámetros de la arquitectura pueden ajustarse según las necesidades específicas.
# Uso básico de `create_and_compile_model`
# ==============================================================================
model = create_and_compile_model(
series = data, # Las 10 series se usan como predictores
levels = ["o3"], # Serie a predecir
lags = 32, # Número de lags a usar como predictores
steps = 24, # Número de steps a predecir
recurrent_layer = "LSTM", # Tipo de capa recurrente ('LSTM', 'GRU', or 'RNN')
recurrent_units = 100, # Número de unidades en la capa recurrente
dense_units = 64 # Número de unidades en la capa densa
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "functional"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 32, 10) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ lstm_1 (LSTM) │ (None, 100) │ 44,400 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 64) │ 6,464 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 24) │ 1,560 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 24, 1) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 52,424 (204.78 KB)
Trainable params: 52,424 (204.78 KB)
Non-trainable params: 0 (0.00 B)
Personalización avanzada
Todos los argumentos que controlan el tipo de capas, número de unidades, funciones de activación y otras opciones pueden personalizarse. Si necesitas una flexibilidad total, también puedes pasar tu propio modelo de Keras para usarlo directamente, en vez de crearlo con la función auxiliar.
Los argumentos recurrent_layers_kwargs y dense_layers_kwargs te permiten especificar los parámetros para las capas recurrentes y densas, respectivamente.
Si usas un diccionario, estos kwargs se aplican a todas las capas del mismo tipo. Por ejemplo, si defines
recurrent_layers_kwargs = {'activation': 'tanh'}, todas las capas recurrentes usarán la función de activacióntanh.También puedes pasar una lista de diccionarios para indicar parámetros diferentes en cada capa. Por ejemplo,
recurrent_layers_kwargs = [{'activation': 'tanh'}, {'activation': 'relu'}]especifica que la primera capa recurrente usarátanhy la segundarelu.
# Uso avanzado de `create_and_compile_model`
# ==============================================================================
model = create_and_compile_model(
series = data,
levels = ["o3"],
lags = 32,
steps = 24,
exog = None, # Sin variables exógenas
recurrent_layer = "LSTM",
recurrent_units = [128, 64],
recurrent_layers_kwargs = [{'activation': 'tanh'}, {'activation': 'relu'}],
dense_units = [128, 64],
dense_layers_kwargs = {'activation': 'relu'},
output_dense_layer_kwargs = {'activation': 'linear'},
compile_kwargs = {'optimizer': Adam(learning_rate=0.001), 'loss': MeanSquaredError()},
model_name = None
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "functional_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 32, 10) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ lstm_1 (LSTM) │ (None, 32, 128) │ 71,168 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ lstm_2 (LSTM) │ (None, 64) │ 49,408 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 128) │ 8,320 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_2 (Dense) │ (None, 64) │ 8,256 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 24) │ 1,560 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 24, 1) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 138,712 (541.84 KB)
Trainable params: 138,712 (541.84 KB)
Non-trainable params: 0 (0.00 B)
Para entender esta función en mayor profundidad, consulta la sección correspondiente en esta guía: Entendiendo create_and_compile_model en profundidad.
Si necesitas definir una arquitectura completamente personalizada, puedes crear tu propio modelo de Keras y usarlo directamente en skforecast.
# Arquitectura del modelo (requiere `pydot` and `graphviz`)
# ==============================================================================
# from keras.utils import plot_model
# plot_model(model, show_shapes=True, show_layer_names=True, to_file='model-architecture.png')

Una vez que el modelo ha sido creado y compilado, el siguiente paso es crear una instancia de ForecasterRnn. Esta clase se encarga de añadir al modelo de deep learning todas las funcionalidades necesarias para que pueda usarse en problemas de predicción de series temporales. Además, es compatible con el resto de las funcionalidades que ofrece skforecast (backtesting, variables exógenas, etc.).
Problemas 1:1 — Serie única, salida única¶
En este escenario, el objetivo es predecir el siguiente valor de una única serie temporal, utilizando solo sus propias observaciones pasadas como predictors. Este tipo de problema se conoce como predicción autorregresiva univariante.
Por ejemplo: Dada una secuencia de valores ${y_{t-3}, y_{t-2}, y_{t-1}}$, predecir $y_{t+1}$.
Single-step forecasting¶
Este es el caso más sencillo para la predicción con redes neuronales recurrentes: tanto el entrenamiento como la predicción se basan en una única serie temporal. En este caso, simplemente hay que pasar esa serie al argumento series de la función create_and_compile_model, y establecer esa misma serie como objetivo mediante el argumento levels. Como se desea predecir solo un valor en el futuro, el parámetro steps debe fijarse en 1.
# Crear modelo
# ==============================================================================
lags = 24
model = create_and_compile_model(
series = data[["o3"]], # Solo la serie 'o3' se usa como predictor
levels = ["o3"], # Serie a predecir
lags = lags, # Número de lags a usar como predictores
steps = 1, # Single-step forecasting
recurrent_layer = "GRU",
recurrent_units = 64,
recurrent_layers_kwargs = {"activation": "tanh"},
dense_units = 32,
compile_kwargs = {'optimizer': Adam(), 'loss': MeanSquaredError()},
model_name = "Single-Series-Single-Step"
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "Single-Series-Single-Step"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 24, 1) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ gru_1 (GRU) │ (None, 64) │ 12,864 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 32) │ 2,080 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 1) │ 33 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 1, 1) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 14,977 (58.50 KB)
Trainable params: 14,977 (58.50 KB)
Non-trainable params: 0 (0.00 B)
El forecaster se crea a partir del modelo y se le proporciona un conjunto de datos de validación para poder evaluar el rendimiento del modelo en cada época de entrenamiento. Además, se utiliza un MinMaxScaler para estandarizar los datos de entrada y salida. Este objeto se encarga de transformar tanto los datos de entrenamiento como las predicciones, asegurando que los resultados se devuelvan a su escala original.
El diccionario fit_kwargs contiene los parámetros que se pasan al método fit del modelo. En este ejemplo, se especifican el número de épocas de entrenamiento, el tamaño del batch, los datos de validación y un callback de EarlyStopping, que detiene el entrenamiento si la pérdida de validación no mejora.
# Crear el Forecaster
# ==============================================================================
forecaster = ForecasterRnn(
estimator=model,
levels=["o3"],
lags=lags, # Debe coincidir con el número de lags usados en el modelo
transformer_series=MinMaxScaler(),
fit_kwargs={
"epochs": 25, # Número de épocas para entrenar el modelo.
"batch_size": 512, # Tamaño del batch para entrenar el modelo.
"callbacks": [
EarlyStopping(monitor="val_loss", patience=3, restore_best_weights=True)
], # Callback para detener el entrenamiento cuando ya no esté aprendiendo más.
"series_val": data_val, # Datos de validación para el entrenamiento del modelo.
},
)
# Entrenar el forecaster
# ==============================================================================
forecaster.fit(data_train[['o3']])
forecaster
Using 'torch' backend with device: cuda Epoch 1/25
39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 47ms/step - loss: 0.0470 - val_loss: 0.0114 Epoch 2/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 62ms/step - loss: 0.0114 - val_loss: 0.0085 Epoch 3/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 48ms/step - loss: 0.0083 - val_loss: 0.0066 Epoch 4/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0067 - val_loss: 0.0058 Epoch 5/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 49ms/step - loss: 0.0060 - val_loss: 0.0056 Epoch 6/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0057 - val_loss: 0.0056 Epoch 7/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0054 - val_loss: 0.0058 Epoch 8/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 62ms/step - loss: 0.0054 - val_loss: 0.0054 Epoch 9/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0053 - val_loss: 0.0055 Epoch 10/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0052 - val_loss: 0.0054 Epoch 11/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0051 - val_loss: 0.0054 Epoch 12/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0053 - val_loss: 0.0053 Epoch 13/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0053 - val_loss: 0.0053 Epoch 14/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 57ms/step - loss: 0.0053 - val_loss: 0.0055 Epoch 15/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 52ms/step - loss: 0.0051 - val_loss: 0.0053 Epoch 16/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 48ms/step - loss: 0.0052 - val_loss: 0.0053 Epoch 17/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 48ms/step - loss: 0.0050 - val_loss: 0.0052 Epoch 18/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0052 - val_loss: 0.0056 Epoch 19/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0052 - val_loss: 0.0052 Epoch 20/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 57ms/step - loss: 0.0049 - val_loss: 0.0051 Epoch 21/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 53ms/step - loss: 0.0051 - val_loss: 0.0051 Epoch 22/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0048 - val_loss: 0.0050 Epoch 23/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 48ms/step - loss: 0.0048 - val_loss: 0.0055 Epoch 24/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0048 - val_loss: 0.0049 Epoch 25/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0049 - val_loss: 0.0050
ForecasterRnn
General Information
- Estimator: Functional
- Layers names: ['series_input', 'gru_1', 'dense_1', 'output_dense_td_layer', 'reshape']
- Lags: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]
- Window size: 24
- Maximum steps to predict: [1]
- Exogenous included: False
- Creation date: 2025-11-27 10:18:56
- Last fit date: 2025-11-27 10:19:46
- Keras backend: torch
- Skforecast version: 0.19.0
- Python version: 3.12.12
- Forecaster id: None
Exogenous Variables
-
None
Data Transformations
- Transformer for series: MinMaxScaler()
- Transformer for exog: MinMaxScaler()
Training Information
- Series names: o3
- Target series (levels): ['o3']
- Training range: [Timestamp('2019-01-01 00:00:00'), Timestamp('2021-03-31 23:00:00')]
- Training index type: DatetimeIndex
- Training index frequency:
Estimator Parameters
-
{'name': 'Single-Series-Single-Step', 'trainable': True, 'layers': [{'module': 'keras.layers', 'class_name': 'InputLayer', 'config': {'batch_shape': (None, 24, 1), 'dtype': 'float32', 'sparse': False, 'ragged': False, 'name': 'series_input'}, 'registered_name': None, 'name': 'series_input', 'inbound_nodes': []}, {'module': 'keras.layers', 'class_name': 'GRU', 'config': {'name': 'gru_1', 'trainable': True, 'dtype': {'module': 'keras', 'class_name': 'DTypePolicy', 'config': {'name': 'float32'}, 'registered_name': None}, 'return_sequences': False, 'return_state': False, 'go_backwards': False, 'stateful': False, 'unroll': False, 'zero_output_for_mask': False, 'units': 64, 'activation': 'tanh', 'recurrent_activation': 'sigmoid', 'use_bias': True, 'kernel_initializer': {'module': 'keras.initializers', 'class_name': 'GlorotUniform', 'config': {'seed': None}, 'registered_name': None}, 'recurrent_initializer': {'module': 'keras.initializers', 'class_name': 'Orthogonal', 'config': {'seed': None, 'gain': 1.0}, 'registered_name': None}, 'bias_initializer': {'module': 'keras.initializers', 'class_name': 'Zeros', 'config': {}, 'registered_name': None}, 'kernel_regularizer': None, 'recurrent_regularizer': None, 'bias_regularizer': None, 'activity_regularizer': None, 'kernel_constraint': None, 'recurrent_constraint': None, 'bias_constraint': None, 'dropout': 0.0, 'recurrent_dropout': 0.0, 'reset_after': True, 'seed': None}, 'registered_name': None, 'build_config': {'input_shape': [None, 24, 1]}, 'name': 'gru_1', 'inbound_nodes': [{'args': ({'class_name': '__keras_tensor__', 'config': {'shape': (None, 24, 1), 'dtype': 'float32', 'keras_history': ['series_input', 0, 0]}},), 'kwargs': {'training': False, 'mask': None}}]}, {'module': 'keras.layers', 'class_name': 'Dense', 'config': {'name': 'dense_1', 'trainable': True, 'dtype': {'module': 'keras', 'class_name': 'DTypePolicy', 'config': {'name': 'float32'}, 'registered_name': None}, 'units': 32, 'activation': 'relu', 'use_bias': True, 'kernel_initializer': {'module': 'keras.initializers', 'class_name': 'GlorotUniform', 'config': {'seed': None}, 'registered_name': None}, 'bias_initializer': {'module': 'keras.initializers', 'class_name': 'Zeros', 'config': {}, 'registered_name': None}, 'kernel_regularizer': None, 'bias_regularizer': None, 'kernel_constraint': None, 'bias_constraint': None}, 'registered_name': None, 'build_config': {'input_shape': [None, 64]}, 'name': 'dense_1', 'inbound_nodes': [{'args': ({'class_name': '__keras_tensor__', 'config': {'shape': (None, 64), 'dtype': 'float32', 'keras_history': ['gru_1', 0, 0]}},), 'kwargs': {}}]}, {'module': 'keras.layers', 'class_name': 'Dense', 'config': {'name': 'output_dense_td_layer', 'trainable': True, 'dtype': {'module': 'keras', 'class_name': 'DTypePolicy', 'config': {'name': 'float32'}, 'registered_name': None}, 'units': 1, 'activation': 'linear', 'use_bias': True, 'kernel_initializer': {'module': 'keras.initializers', 'class_name': 'GlorotUniform', 'config': {'seed': None}, 'registered_name': None}, 'bias_initializer': {'module': 'keras.initializers', 'class_name': 'Zeros', 'config': {}, 'registered_name': None}, 'kernel_regularizer': None, 'bias_regularizer': None, 'kernel_constraint': None, 'bias_constraint': None}, 'registered_name': None, 'build_config': {'input_shape': [None, 32]}, 'name': 'output_dense_td_layer', 'inbound_nodes': [{'args': ({'class_name': '__keras_tensor__', 'config': {'shape': (None, 32), 'dtype': 'float32', 'keras_history': ['dense_1', 0, 0]}},), 'kwargs': {}}]}, {'module': 'keras.layers', 'class_name': 'Reshape', 'config': {'name': 'reshape', 'trainable': True, 'dtype': {'module': 'keras', 'class_name': 'DTypePolicy', 'config': {'name': 'float32'}, 'registered_name': None}, 'target_shape': (1, 1)}, 'registered_name': None, 'build_config': {'input_shape': [None, 1]}, 'name': 'reshape', 'inbound_nodes': [{'args': ({'class_name': '__keras_tensor__', 'config': {'shape': (None, 1), 'dtype': 'float32', 'keras_history': ['output_dense_td_layer', 0, 0]}},), 'kwargs': {}}]}], 'input_layers': [['series_input', 0, 0]], 'output_layers': [['reshape', 0, 0]]}
Compile Parameters
-
{'optimizer': {'module': 'keras.src.backend.torch.optimizers.torch_adam', 'class_name': 'Adam', 'config': {'name': 'adam', 'learning_rate': 0.0010000000474974513, 'weight_decay': None, 'clipnorm': None, 'global_clipnorm': None, 'clipvalue': None, 'use_ema': False, 'ema_momentum': 0.99, 'ema_overwrite_frequency': None, 'loss_scale_factor': None, 'gradient_accumulation_steps': None, 'beta_1': 0.9, 'beta_2': 0.999, 'epsilon': 1e-07, 'amsgrad': False}, 'registered_name': 'Adam'}, 'loss': {'module': 'keras.losses', 'class_name': 'MeanSquaredError', 'config': {'name': 'mean_squared_error', 'reduction': 'sum_over_batch_size'}, 'registered_name': None}, 'loss_weights': None, 'metrics': None, 'weighted_metrics': None, 'run_eagerly': False, 'steps_per_execution': 1, 'jit_compile': False}
Fit Kwargs
-
{'epochs': 25, 'batch_size': 512, 'callbacks': [
✏️ Note
La librería skforecast es totalmente compatible con GPUs. Consulta la sección Ejecutando en GPU más abajo en este documento para más información.
En los modelos de deep learning es importante controlar el sobreajuste (overfitting), que ocurre cuando un modelo obtiene buenos resultados con los datos de entrenamiento pero un rendimiento pobre con datos nuevos o no vistos. Una estrategia habitual para evitarlo es utilizar un callback de Keras, como EarlyStopping, que detiene el entrenamiento si la pérdida de validación deja de mejorar.
Otra práctica muy útil es visualizar la pérdida de entrenamiento y validación después de cada época. Esto te permite ver cómo está aprendiendo el modelo y detectar posibles síntomas de sobreajuste.

Explicación gráfica del sobreajuste. Fuente: https://datahacker.rs/018-pytorch-popular-techniques-to-prevent-the-overfitting-in-a-neural-networks/.
# Seguimiento del entrenamiento y overfitting
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3))
_ = forecaster.plot_history(ax=ax)
En la gráfica anterior, la pérdida de entrenamiento (azul) disminuye rápidamente durante las dos primeras épocas, lo que indica que el modelo está capturando rápidamente los patrones principales de los datos. La pérdida de validación (rojo) comienza baja y se mantiene estable a lo largo del proceso de entrenamiento, siguiendo de cerca la pérdida de entrenamiento. Esto sugiere que:
El modelo no está sobreajustando, ya que la pérdida de validación se mantiene cercana a la de entrenamiento en todas las épocas.
Ambas pérdidas disminuyen y se estabilizan juntas, lo que indica una buena generalización y un aprendizaje efectivo.
No se observa divergencia, que aparecería si la pérdida de validación aumentara mientras la de entrenamiento sigue disminuyendo.
Cuando la magnitud de la función de coste (loss) es muy diferente entre entrenamiento y validación, se recomienda graficar los valores de entrenamiento y validación utilizando ejes y escalas diferentes. Este enfoque permite una visualización más clara de las tendencias de loss, facilitando la identificación de problemas de sobreajuste o subajuste en el modelo.
# Seguimiento del entrenamiento con ejes y escalas diferentes
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 3))
epochs = np.arange(len(forecaster.history_['loss']))
p1, = ax.plot(epochs, forecaster.history_['loss'], color='tab:blue', label='loss')
ax.set_ylabel('loss', color='tab:blue')
ax.tick_params(axis='y', labelcolor='tab:blue')
ax2 = ax.twinx()
p2, = ax2.plot(epochs, forecaster.history_['val_loss'], color='tab:orange', label='val_loss')
ax2.set_ylabel('val_loss', color='tab:orange')
ax2.tick_params(axis='y', labelcolor='tab:orange')
ax.legend(handles=[p1, p2], loc='upper right')
ax.set_title('Training and Validation Loss over Epochs')
plt.show()
Una vez que el forecaster ha sido entrenado, se pueden obtener las predicciones. Si el parámetro steps es None en el método predict, el forecaster predecirá todos los pasos futuros aprendidos, forecaster.max_step.
# Forecaster steps disponibles
# ==============================================================================
forecaster.max_step
np.int64(1)
# Predicción
# ==============================================================================
predictions = forecaster.predict(steps=None) # Igual que steps=1
predictions
| level | pred | |
|---|---|---|
| 2021-04-01 | o3 | 47.151917 |
Para obtener una estimación robusta de la capacidad predictiva del modelo, se realiza un proceso de backtesting. El proceso de backtesting consiste en generar una predicción para cada observación del conjunto de test, siguiendo el mismo procedimiento que se seguiría si el modelo estuviese en producción, y finalmente comparar el valor predicho con el valor real.
✏️ Note
En el paso anterior se ha utilizado la partición de validación para comprobar que el modelo aprende y para identificar el número de epocas con el que se alcanza el mejor rendimiento. En el siguiente paso (backtesting) la partición de validación se incluye en el conjunto de entrenamiento para aprovechar todos los datos disponibles antes de evaluar el modelo en el conjunto de test. Se emplea el metodo forecaster.set_fit_kwargs() para actualizar los argumentos de ajuste del modelo antes del proceso de backtesting.
# Backtesting con datos de test
# ==============================================================================
cv = TimeSeriesFold(
steps = forecaster.max_step,
initial_train_size = len(data.loc[:end_validation, :]), # Training + Validation Data
refit = False
)
# Ahora la partición de validación se usa como parte del fit inicial
# Se emplean las epocas identicas en el paso anterior por el early stopping
forecaster.set_fit_kwargs({"epochs": 15,"batch_size": 512})
metrics, predictions = backtesting_forecaster_multiseries(
forecaster = forecaster,
series = data[['o3']],
cv = cv,
levels = forecaster.levels,
metric = "mean_absolute_error",
verbose = False # Set to True for detailed output
)
Using 'torch' backend with device: cuda Epoch 1/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0048 Epoch 2/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0047 Epoch 3/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0048 Epoch 4/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0049 Epoch 5/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 43ms/step - loss: 0.0050 Epoch 6/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 51ms/step - loss: 0.0048 Epoch 7/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0047 Epoch 8/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0048 Epoch 9/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0050 Epoch 10/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0050 Epoch 11/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 49ms/step - loss: 0.0048 Epoch 12/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0047 Epoch 13/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0046 Epoch 14/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0049 Epoch 15/15 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0045
0%| | 0/2208 [00:00<?, ?it/s]
# Métrica de backtesting
# ==============================================================================
metrics
| levels | mean_absolute_error | |
|---|---|---|
| 0 | o3 | 5.809888 |
# Predicciones de backtesting
# ==============================================================================
predictions.head(4)
| level | fold | pred | |
|---|---|---|---|
| 2021-10-01 00:00:00 | o3 | 0 | 53.515694 |
| 2021-10-01 01:00:00 | o3 | 1 | 58.752594 |
| 2021-10-01 02:00:00 | o3 | 2 | 62.574272 |
| 2021-10-01 03:00:00 | o3 | 3 | 62.523232 |
# Gráfico de las predicciones vs valores reales en el conjunto de test
# ==============================================================================
fig = go.Figure()
trace1 = go.Scatter(x=data_test.index, y=data_test['o3'], name="test", mode="lines")
trace2 = go.Scatter(
x=predictions.index,
y=predictions.loc[predictions["level"] == "o3", "pred"],
name="predictions", mode="lines"
)
fig.add_trace(trace1)
fig.add_trace(trace2)
fig.update_layout(
title="Prediction vs real values in the test set",
xaxis_title="Date time",
yaxis_title="O3",
width=800,
height=400,
margin=dict(l=20, r=20, t=35, b=20),
legend=dict(orientation="h", yanchor="top", y=1.05, xanchor="left", x=0)
)
fig.show()
# Error en % respecto a la media de la serie
# ==============================================================================
rel_mse = 100 * metrics.loc[0, 'mean_absolute_error'] / np.mean(data["o3"])
print(f"Media de la serie: {np.mean(data['o3']):0.2f}")
print(f"Error (mae) relativo: {rel_mse:0.2f} %")
Media de la serie: 54.52 Error (mae) relativo: 10.66 %
Multi-step forecasting¶
En este caso, el objetivo es predecir varios valores futuros de una única serie temporal utilizando solo sus propias observaciones pasadas como predictores. A esto se le denomina predicción univariante multi-paso.
Por ejemplo: Dada una secuencia de valores ${y_{t-24}, ..., y_{t-1}}$, predecir ${y_{t+1}, y_{t+2}, ..., y_{t+h}}$, donde $n$ es el horizonte de predicción (número de pasos a futuro).
Esta configuración es habitual cuando se quiere predecir varios pasos a futuro (por ejemplo, las próximas 24 horas de concentración de ozono).
Arquitectura del modelo
Puedes emplear una arquitectura de red similar a la del caso de un solo paso, pero predecir varios pasos en el futuro suele beneficiarse de aumentar la capacidad del modelo (por ejemplo, añadiendo más unidades en las capas LSTM/GRU o capas densas adicionales). Esto permite al modelo capturar mejor la complejidad de anticipar varios valores a la vez.
# Create model
# ==============================================================================
lags = 24
model = create_and_compile_model(
series = data[["o3"]], # Solo la serie 'o3' se usa como predictor
levels = ["o3"], # Serie a predecir
lags = lags, # Número de lags a usar como predictores
steps = 24, # Multi-step forecasting
recurrent_layer = "GRU",
recurrent_units = 128,
recurrent_layers_kwargs = {"activation": "tanh"},
dense_units = 64,
compile_kwargs = {'optimizer': 'adam', 'loss': 'mse'},
model_name = "Single-Series-Multi-Step"
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "Single-Series-Multi-Step"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 24, 1) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ gru_1 (GRU) │ (None, 128) │ 50,304 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 64) │ 8,256 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 24) │ 1,560 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 24, 1) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 60,120 (234.84 KB)
Trainable params: 60,120 (234.84 KB)
Non-trainable params: 0 (0.00 B)
✏️ Note
El parámetro fit_kwargs permite personalizar cualquier aspecto del proceso de entrenamiento del modelo, pasando argumentos directamente al método Model.fit() de Keras. Por ejemplo, puedes especificar el número de épocas de entrenamiento, el tamaño del batch y cualquier callback que desees utilizar.
En el ejemplo, el modelo se entrena durante 50 épocas con un batch size de 512. El callback EarlyStopping monitoriza la pérdida de validación y detiene automáticamente el entrenamiento si no mejora durante 3 épocas consecutivas (patience=3). Esto ayuda a prevenir el sobreajuste y a ahorrar tiempo de computación.
También puedes añadir otros callbacks, como ModelCheckpoint para guardar el modelo en cada época, o TensorBoard para visualizar en tiempo real las métricas de entrenamiento y validación.
# Crear el Forecaster
# ==============================================================================
forecaster = ForecasterRnn(
estimator=model,
levels=["o3"],
lags=lags, # Debe coincidir con el número de lags usados en el modelo
transformer_series=MinMaxScaler(),
fit_kwargs={
"epochs": 25, # Número de épocas para entrenar el modelo.
"batch_size": 512, # Tamaño del batch para entrenar el modelo.
"callbacks": [
EarlyStopping(monitor="val_loss", patience=3, restore_best_weights=True)
], # Callback para detener el entrenamiento cuando ya no esté aprendiendo más.
"series_val": data_val, # Datos de validación para el entrenamiento del modelo.
},
)
# Entrenar el forecaster
# ==============================================================================
forecaster.fit(data_train[['o3']])
forecaster
Using 'torch' backend with device: cuda Epoch 1/25 1/39 ━━━━━━━━━━━━━━━━━━━━ 1s 49ms/step - loss: 0.1796
39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 57ms/step - loss: 0.1104 - val_loss: 0.0299 Epoch 2/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 63ms/step - loss: 0.0293 - val_loss: 0.0264 Epoch 3/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0261 - val_loss: 0.0236 Epoch 4/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 49ms/step - loss: 0.0244 - val_loss: 0.0213 Epoch 5/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 48ms/step - loss: 0.0225 - val_loss: 0.0190 Epoch 6/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0207 - val_loss: 0.0185 Epoch 7/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 61ms/step - loss: 0.0202 - val_loss: 0.0178 Epoch 8/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 48ms/step - loss: 0.0199 - val_loss: 0.0171 Epoch 9/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0195 - val_loss: 0.0173 Epoch 10/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 49ms/step - loss: 0.0192 - val_loss: 0.0171 Epoch 11/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 48ms/step - loss: 0.0189 - val_loss: 0.0170 Epoch 12/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 49ms/step - loss: 0.0186 - val_loss: 0.0164 Epoch 13/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 61ms/step - loss: 0.0184 - val_loss: 0.0165 Epoch 14/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 48ms/step - loss: 0.0181 - val_loss: 0.0166 Epoch 15/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 48ms/step - loss: 0.0182 - val_loss: 0.0164
ForecasterRnn
General Information
- Estimator: Functional
- Layers names: ['series_input', 'gru_1', 'dense_1', 'output_dense_td_layer', 'reshape']
- Lags: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]
- Window size: 24
- Maximum steps to predict: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]
- Exogenous included: False
- Creation date: 2025-11-27 10:21:45
- Last fit date: 2025-11-27 10:22:15
- Keras backend: torch
- Skforecast version: 0.19.0
- Python version: 3.12.12
- Forecaster id: None
Exogenous Variables
-
None
Data Transformations
- Transformer for series: MinMaxScaler()
- Transformer for exog: MinMaxScaler()
Training Information
- Series names: o3
- Target series (levels): ['o3']
- Training range: [Timestamp('2019-01-01 00:00:00'), Timestamp('2021-03-31 23:00:00')]
- Training index type: DatetimeIndex
- Training index frequency:
Estimator Parameters
-
{'name': 'Single-Series-Multi-Step', 'trainable': True, 'layers': [{'module': 'keras.layers', 'class_name': 'InputLayer', 'config': {'batch_shape': (None, 24, 1), 'dtype': 'float32', 'sparse': False, 'ragged': False, 'name': 'series_input'}, 'registered_name': None, 'name': 'series_input', 'inbound_nodes': []}, {'module': 'keras.layers', 'class_name': 'GRU', 'config': {'name': 'gru_1', 'trainable': True, 'dtype': {'module': 'keras', 'class_name': 'DTypePolicy', 'config': {'name': 'float32'}, 'registered_name': None}, 'return_sequences': False, 'return_state': False, 'go_backwards': False, 'stateful': False, 'unroll': False, 'zero_output_for_mask': False, 'units': 128, 'activation': 'tanh', 'recurrent_activation': 'sigmoid', 'use_bias': True, 'kernel_initializer': {'module': 'keras.initializers', 'class_name': 'GlorotUniform', 'config': {'seed': None}, 'registered_name': None}, 'recurrent_initializer': {'module': 'keras.initializers', 'class_name': 'Orthogonal', 'config': {'seed': None, 'gain': 1.0}, 'registered_name': None}, 'bias_initializer': {'module': 'keras.initializers', 'class_name': 'Zeros', 'config': {}, 'registered_name': None}, 'kernel_regularizer': None, 'recurrent_regularizer': None, 'bias_regularizer': None, 'activity_regularizer': None, 'kernel_constraint': None, 'recurrent_constraint': None, 'bias_constraint': None, 'dropout': 0.0, 'recurrent_dropout': 0.0, 'reset_after': True, 'seed': None}, 'registered_name': None, 'build_config': {'input_shape': [None, 24, 1]}, 'name': 'gru_1', 'inbound_nodes': [{'args': ({'class_name': '__keras_tensor__', 'config': {'shape': (None, 24, 1), 'dtype': 'float32', 'keras_history': ['series_input', 0, 0]}},), 'kwargs': {'training': False, 'mask': None}}]}, {'module': 'keras.layers', 'class_name': 'Dense', 'config': {'name': 'dense_1', 'trainable': True, 'dtype': {'module': 'keras', 'class_name': 'DTypePolicy', 'config': {'name': 'float32'}, 'registered_name': None}, 'units': 64, 'activation': 'relu', 'use_bias': True, 'kernel_initializer': {'module': 'keras.initializers', 'class_name': 'GlorotUniform', 'config': {'seed': None}, 'registered_name': None}, 'bias_initializer': {'module': 'keras.initializers', 'class_name': 'Zeros', 'config': {}, 'registered_name': None}, 'kernel_regularizer': None, 'bias_regularizer': None, 'kernel_constraint': None, 'bias_constraint': None}, 'registered_name': None, 'build_config': {'input_shape': [None, 128]}, 'name': 'dense_1', 'inbound_nodes': [{'args': ({'class_name': '__keras_tensor__', 'config': {'shape': (None, 128), 'dtype': 'float32', 'keras_history': ['gru_1', 0, 0]}},), 'kwargs': {}}]}, {'module': 'keras.layers', 'class_name': 'Dense', 'config': {'name': 'output_dense_td_layer', 'trainable': True, 'dtype': {'module': 'keras', 'class_name': 'DTypePolicy', 'config': {'name': 'float32'}, 'registered_name': None}, 'units': 24, 'activation': 'linear', 'use_bias': True, 'kernel_initializer': {'module': 'keras.initializers', 'class_name': 'GlorotUniform', 'config': {'seed': None}, 'registered_name': None}, 'bias_initializer': {'module': 'keras.initializers', 'class_name': 'Zeros', 'config': {}, 'registered_name': None}, 'kernel_regularizer': None, 'bias_regularizer': None, 'kernel_constraint': None, 'bias_constraint': None}, 'registered_name': None, 'build_config': {'input_shape': [None, 64]}, 'name': 'output_dense_td_layer', 'inbound_nodes': [{'args': ({'class_name': '__keras_tensor__', 'config': {'shape': (None, 64), 'dtype': 'float32', 'keras_history': ['dense_1', 0, 0]}},), 'kwargs': {}}]}, {'module': 'keras.layers', 'class_name': 'Reshape', 'config': {'name': 'reshape', 'trainable': True, 'dtype': {'module': 'keras', 'class_name': 'DTypePolicy', 'config': {'name': 'float32'}, 'registered_name': None}, 'target_shape': (24, 1)}, 'registered_name': None, 'build_config': {'input_shape': [None, 24]}, 'name': 'reshape', 'inbound_nodes': [{'args': ({'class_name': '__keras_tensor__', 'config': {'shape': (None, 24), 'dtype': 'float32', 'keras_history': ['output_dense_td_layer', 0, 0]}},), 'kwargs': {}}]}], 'input_layers': [['series_input', 0, 0]], 'output_layers': [['reshape', 0, 0]]}
Compile Parameters
-
{'optimizer': {'module': 'keras.src.backend.torch.optimizers.torch_adam', 'class_name': 'Adam', 'config': {'name': 'adam', 'learning_rate': 0.0010000000474974513, 'weight_decay': None, 'clipnorm': None, 'global_clipnorm': None, 'clipvalue': None, 'use_ema': False, 'ema_momentum': 0.99, 'ema_overwrite_frequency': None, 'loss_scale_factor': None, 'gradient_accumulation_steps': None, 'beta_1': 0.9, 'beta_2': 0.999, 'epsilon': 1e-07, 'amsgrad': False}, 'registered_name': 'Adam'}, 'loss': 'mse', 'loss_weights': None, 'metrics': None, 'weighted_metrics': None, 'run_eagerly': False, 'steps_per_execution': 1, 'jit_compile': False}
Fit Kwargs
-
{'epochs': 25, 'batch_size': 512, 'callbacks': [
# Seguimiento del entrenamiento y overfitting
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3))
_ = forecaster.plot_history(ax=ax)
En este caso, se espera que la calidad de las predicciones sea inferior a la del ejemplo anterior, como se observa en los valores más altos de la pérdida a lo largo de las épocas. La explicación es sencilla: ahora el modelo tiene que predecir 24 valores en cada paso, en lugar de solo 1. Por tanto, la pérdida de validación es mayor, ya que refleja el error combinado de las 24 predicciones, en vez del error de una sola predicción.
# Forecaster steps disponibles
# ==============================================================================
forecaster.max_step
np.int64(24)
# Predicción
# ==============================================================================
predictions = forecaster.predict(steps=24) # Igual que steps=None
predictions
| level | pred | |
|---|---|---|
| 2021-04-01 00:00:00 | o3 | 52.413437 |
| 2021-04-01 01:00:00 | o3 | 51.247059 |
| 2021-04-01 02:00:00 | o3 | 44.847496 |
| 2021-04-01 03:00:00 | o3 | 39.121109 |
| 2021-04-01 04:00:00 | o3 | 38.078609 |
| 2021-04-01 05:00:00 | o3 | 33.383938 |
| 2021-04-01 06:00:00 | o3 | 28.030472 |
| 2021-04-01 07:00:00 | o3 | 25.476110 |
| 2021-04-01 08:00:00 | o3 | 29.781727 |
| 2021-04-01 09:00:00 | o3 | 36.966896 |
| 2021-04-01 10:00:00 | o3 | 46.440903 |
| 2021-04-01 11:00:00 | o3 | 57.859703 |
| 2021-04-01 12:00:00 | o3 | 69.811684 |
| 2021-04-01 13:00:00 | o3 | 78.114143 |
| 2021-04-01 14:00:00 | o3 | 82.805435 |
| 2021-04-01 15:00:00 | o3 | 85.240074 |
| 2021-04-01 16:00:00 | o3 | 87.526939 |
| 2021-04-01 17:00:00 | o3 | 84.049828 |
| 2021-04-01 18:00:00 | o3 | 81.173363 |
| 2021-04-01 19:00:00 | o3 | 71.725952 |
| 2021-04-01 20:00:00 | o3 | 69.047241 |
| 2021-04-01 21:00:00 | o3 | 62.915886 |
| 2021-04-01 22:00:00 | o3 | 59.307892 |
| 2021-04-01 23:00:00 | o3 | 61.420410 |
También se pueden predecir steps especificos, siempre y cuando se encuentren dentro del horizonte de predicción definido en el modelo.
# Predicción steps especificos
# ==============================================================================
predictions = forecaster.predict(steps=[1, 3])
predictions
| level | pred | |
|---|---|---|
| 2021-04-01 00:00:00 | o3 | 52.413437 |
| 2021-04-01 02:00:00 | o3 | 44.847496 |
# Backtesting con datos de test
# ==============================================================================
cv = TimeSeriesFold(
steps = forecaster.max_step,
initial_train_size = len(data.loc[:end_validation, :]), # Training + Validation Data
refit = False
)
# Ahora la partición de validación se usa como parte del fit inicial
# Se emplean las epocas identicas en el paso anterior por el early stopping
forecaster.set_fit_kwargs({"epochs": 18,"batch_size": 512})
metrics, predictions = backtesting_forecaster_multiseries(
forecaster = forecaster,
series = data[['o3']],
cv = cv,
levels = forecaster.levels,
metric = "mean_absolute_error",
verbose = False,
suppress_warnings = True
)
Using 'torch' backend with device: cuda Epoch 1/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0180 Epoch 2/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0179 Epoch 3/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 53ms/step - loss: 0.0178 Epoch 4/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0178 Epoch 5/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 43ms/step - loss: 0.0175 Epoch 6/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0176 Epoch 7/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0173 Epoch 8/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0173 Epoch 9/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 49ms/step - loss: 0.0173 Epoch 10/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 43ms/step - loss: 0.0172 Epoch 11/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 43ms/step - loss: 0.0172 Epoch 12/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0171 Epoch 13/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0170 Epoch 14/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 50ms/step - loss: 0.0170 Epoch 15/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 45ms/step - loss: 0.0168 Epoch 16/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0168 Epoch 17/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0168 Epoch 18/18 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0166
0%| | 0/92 [00:00<?, ?it/s]
# Backtesting metrics
# ==============================================================================
metric_single_series = metrics.loc[metrics["levels"] == "o3", "mean_absolute_error"].iat[0]
metrics
| levels | mean_absolute_error | |
|---|---|---|
| 0 | o3 | 11.0835 |
# Predicciones de backtesting
# ==============================================================================
predictions
| level | fold | pred | |
|---|---|---|---|
| 2021-10-01 00:00:00 | o3 | 0 | 55.272926 |
| 2021-10-01 01:00:00 | o3 | 0 | 54.927097 |
| 2021-10-01 02:00:00 | o3 | 0 | 52.762840 |
| 2021-10-01 03:00:00 | o3 | 0 | 49.187874 |
| 2021-10-01 04:00:00 | o3 | 0 | 47.400066 |
| ... | ... | ... | ... |
| 2021-12-31 19:00:00 | o3 | 91 | 17.809635 |
| 2021-12-31 20:00:00 | o3 | 91 | 16.677813 |
| 2021-12-31 21:00:00 | o3 | 91 | 20.568716 |
| 2021-12-31 22:00:00 | o3 | 91 | 25.254272 |
| 2021-12-31 23:00:00 | o3 | 91 | 26.961819 |
2208 rows × 3 columns
# Gráfico de las predicciones vs valores reales en el conjunto de test
# ==============================================================================
fig = go.Figure()
trace1 = go.Scatter(x=data_test.index, y=data_test['o3'], name="test", mode="lines")
trace2 = go.Scatter(
x=predictions.index,
y=predictions.loc[predictions["level"] == "o3", "pred"],
name="predictions", mode="lines"
)
fig.add_trace(trace1)
fig.add_trace(trace2)
fig.update_layout(
title="Prediction vs real values in the test set",
xaxis_title="Date time",
yaxis_title="O3",
width=800,
height=400,
margin=dict(l=20, r=20, t=35, b=20),
legend=dict(orientation="h", yanchor="top", y=1.05, xanchor="left", x=0)
)
fig.show()
# Error mse en % respecto a la media de la serie
# ==============================================================================
rel_mse = 100 * metrics.loc[0, 'mean_absolute_error'] / np.mean(data["o3"])
print(f"Media de la serie: {np.mean(data['o3']):0.2f}")
print(f"Error mse relativo: {rel_mse:0.2f} %")
Media de la serie: 54.52 Error mse relativo: 20.33 %
En este caso la predicción es empeora respecto al caso anterior. Esto es de esperar ya que el modelo tiene que predecir 24 valores en lugar de 1.
Problemas N:1 — Multiserie, salida única¶
En este escenario, el objetivo es predecir los valores futuros de una única serie objetivo utilizando los valores pasados de múltiples series relacionadas como predictores. Esto se conoce como predicción multivariante, donde el modelo emplea los datos históricos de varias variables para mejorar la predicción de una serie específica.
Por ejemplo: Supón que quieres predecir la concentración de ozono (o3) para las próximas 24 horas. Además de los valores pasados de o3, puedes incluir otras series—como la temperatura, la velocidad del viento u otras concentraciones de contaminantes—como variables predictoras. El modelo utilizará la información combinada de todas las series disponibles para realizar una predicción más precisa.
Configuración del modelo
Para abordar este tipo de problema, la arquitectura de la red neuronal se vuelve un poco más compleja. Se añade una capa recurrente adicional para procesar la información de las distintas series de entrada, y otra capa densa (totalmente conectada) para trabajar sobre la salida de la capa recurrente. Con skforecast, construir un modelo de este tipo es sencillo: basta con pasar una lista de enteros a los argumentos recurrent_units y dense_units para añadir múltiples capas recurrentes y densas según sea necesario.
# Creación del modelo
# ==============================================================================
lags = 24
model = create_and_compile_model(
series = data, # DataFrame con todas las series (predictores)
levels = ["o3"], # Serie a predecir
lags = lags, # Numero de lags a usar como predictores
steps = 24, # Multi-step forecasting
recurrent_layer = "GRU",
recurrent_units = [128, 64],
recurrent_layers_kwargs = {"activation": "tanh"},
dense_units = [64, 32],
compile_kwargs = {'optimizer': 'adam', 'loss': 'mse'},
model_name = "MultiVariate-Multi-Step"
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "MultiVariate-Multi-Step"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 24, 10) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ gru_1 (GRU) │ (None, 24, 128) │ 53,760 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ gru_2 (GRU) │ (None, 64) │ 37,248 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 64) │ 4,160 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_2 (Dense) │ (None, 32) │ 2,080 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 24) │ 792 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 24, 1) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 98,040 (382.97 KB)
Trainable params: 98,040 (382.97 KB)
Non-trainable params: 0 (0.00 B)
# Creación del Forecaster
# ==============================================================================
forecaster = ForecasterRnn(
estimator=model,
levels=["o3"],
lags=lags,
transformer_series=MinMaxScaler(),
fit_kwargs={
"epochs": 25,
"batch_size": 512,
"callbacks": [
EarlyStopping(monitor="val_loss", patience=3, restore_best_weights=True)
],
"series_val": data_val,
},
)
# Fit forecaster
# ==============================================================================
forecaster.fit(data_train)
Using 'torch' backend with device: cuda Epoch 1/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 91ms/step - loss: 0.1271 - val_loss: 0.0690 Epoch 2/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 104ms/step - loss: 0.0437 - val_loss: 0.0278 Epoch 3/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 91ms/step - loss: 0.0266 - val_loss: 0.0249 Epoch 4/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 91ms/step - loss: 0.0251 - val_loss: 0.0230 Epoch 5/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 104ms/step - loss: 0.0228 - val_loss: 0.0196 Epoch 6/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 92ms/step - loss: 0.0208 - val_loss: 0.0179 Epoch 7/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 90ms/step - loss: 0.0188 - val_loss: 0.0170 Epoch 8/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 103ms/step - loss: 0.0180 - val_loss: 0.0165 Epoch 9/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 92ms/step - loss: 0.0175 - val_loss: 0.0157 Epoch 10/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 91ms/step - loss: 0.0170 - val_loss: 0.0157 Epoch 11/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 105ms/step - loss: 0.0166 - val_loss: 0.0154 Epoch 12/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 92ms/step - loss: 0.0165 - val_loss: 0.0156 Epoch 13/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 90ms/step - loss: 0.0163 - val_loss: 0.0154 Epoch 14/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 97ms/step - loss: 0.0160 - val_loss: 0.0154 Epoch 15/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 99ms/step - loss: 0.0157 - val_loss: 0.0152 Epoch 16/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 101ms/step - loss: 0.0157 - val_loss: 0.0153 Epoch 17/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 94ms/step - loss: 0.0155 - val_loss: 0.0150 Epoch 18/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 101ms/step - loss: 0.0155 - val_loss: 0.0151 Epoch 19/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 92ms/step - loss: 0.0152 - val_loss: 0.0156 Epoch 20/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 91ms/step - loss: 0.0154 - val_loss: 0.0152
# Seguimiento del entrenamiento y overfitting
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3))
_ = forecaster.plot_history(ax=ax)
# Predicción
# ==============================================================================
predictions = forecaster.predict()
predictions.head(4)
| level | pred | |
|---|---|---|
| 2021-04-01 00:00:00 | o3 | 49.468742 |
| 2021-04-01 01:00:00 | o3 | 46.477806 |
| 2021-04-01 02:00:00 | o3 | 39.386822 |
| 2021-04-01 03:00:00 | o3 | 35.604961 |
# Backtesting con datos de test
# ==============================================================================
cv = TimeSeriesFold(
steps = forecaster.max_step,
initial_train_size = len(data.loc[:end_validation, :]), # Training + Validation Data
refit = False
)
# Ahora la partición de validación se usa como parte del fit inicial
# Se emplean las epocas identicas en el paso anterior por el early stopping
forecaster.set_fit_kwargs({"epochs": 23,"batch_size": 512})
metrics, predictions = backtesting_forecaster_multiseries(
forecaster = forecaster,
series = data,
cv = cv,
levels = forecaster.levels,
metric = "mean_absolute_error",
suppress_warnings = True,
verbose = False
)
Using 'torch' backend with device: cuda Epoch 1/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 80ms/step - loss: 0.0154 Epoch 2/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 81ms/step - loss: 0.0153 Epoch 3/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 91ms/step - loss: 0.0151 Epoch 4/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 81ms/step - loss: 0.0149 Epoch 5/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 80ms/step - loss: 0.0149 Epoch 6/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 92ms/step - loss: 0.0148 Epoch 7/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 80ms/step - loss: 0.0146 Epoch 8/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 79ms/step - loss: 0.0146 Epoch 9/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 93ms/step - loss: 0.0145 Epoch 10/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 80ms/step - loss: 0.0144 Epoch 11/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 80ms/step - loss: 0.0143 Epoch 12/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 93ms/step - loss: 0.0142 Epoch 13/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 79ms/step - loss: 0.0140 Epoch 14/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 81ms/step - loss: 0.0140 Epoch 15/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 93ms/step - loss: 0.0138 Epoch 16/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 80ms/step - loss: 0.0138 Epoch 17/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 82ms/step - loss: 0.0137 Epoch 18/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 93ms/step - loss: 0.0137 Epoch 19/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 81ms/step - loss: 0.0136 Epoch 20/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 80ms/step - loss: 0.0134 Epoch 21/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 92ms/step - loss: 0.0136 Epoch 22/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 79ms/step - loss: 0.0134 Epoch 23/23 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 89ms/step - loss: 0.0132
0%| | 0/92 [00:00<?, ?it/s]
# Métricas de error de backtesting
# ==============================================================================
metric_multivariate = metrics.loc[metrics["levels"] == "o3", "mean_absolute_error"].iat[0]
metrics
| levels | mean_absolute_error | |
|---|---|---|
| 0 | o3 | 10.895787 |
# Predicciones de backtesting
# ==============================================================================
predictions
| level | fold | pred | |
|---|---|---|---|
| 2021-10-01 00:00:00 | o3 | 0 | 58.028431 |
| 2021-10-01 01:00:00 | o3 | 0 | 52.990044 |
| 2021-10-01 02:00:00 | o3 | 0 | 44.850399 |
| 2021-10-01 03:00:00 | o3 | 0 | 40.669624 |
| 2021-10-01 04:00:00 | o3 | 0 | 37.451221 |
| ... | ... | ... | ... |
| 2021-12-31 19:00:00 | o3 | 91 | 19.612408 |
| 2021-12-31 20:00:00 | o3 | 91 | 18.910252 |
| 2021-12-31 21:00:00 | o3 | 91 | 14.360760 |
| 2021-12-31 22:00:00 | o3 | 91 | 19.938372 |
| 2021-12-31 23:00:00 | o3 | 91 | 20.645273 |
2208 rows × 3 columns
# Error mse en % respecto a la media de la serie
# ==============================================================================
rel_mse = 100 * metrics.loc[0, 'mean_absolute_error'] / np.mean(data["o3"])
print(f"Media de la serie: {np.mean(data['o3']):0.2f}")
print(f"Error mse relativo: {rel_mse:0.2f} %")
Media de la serie: 54.52 Error mse relativo: 19.99 %
# Gráfico de las predicciones vs valores reales en el conjunto de test
# ==============================================================================
fig = go.Figure()
trace1 = go.Scatter(x=data_test.index, y=data_test['o3'], name="test", mode="lines")
trace2 = go.Scatter(
x=predictions.index,
y=predictions.loc[predictions["level"] == "o3", "pred"],
name="predictions", mode="lines"
)
fig.add_trace(trace1)
fig.add_trace(trace2)
fig.update_layout(
title="Prediction vs real values in the test set",
xaxis_title="Date time",
yaxis_title="O3",
width=800,
height=400,
margin=dict(l=20, r=20, t=35, b=20),
legend=dict(orientation="h", yanchor="top", y=1.05, xanchor="left", x=0)
)
fig.show()
Cuando se utilizan varias series temporales como predictores, suele esperarse que el modelo genere predicciones más precisas para la serie objetivo. Sin embargo, en algunos casos, las predicciones pueden ser incluso peores que cuando solo se utiliza una serie como entrada. Esto puede ocurrir si las series adicionales que se emplean como predictores no están fuertemente relacionadas con la serie objetivo. Como resultado, el modelo no logra aprender relaciones significativas, y la información extra no mejora el rendimiento; de hecho, incluso puede introducir ruido.
Problemas N:M — Multiserie, múltiples salidas¶
En este escenario, el objetivo es predecir varios valores futuros para varias series temporales a la vez, utilizando como entrada los datos históricos de todas las series disponibles. A esto se le conoce como predicción multivariante-multisalida.
Con este enfoque, un solo modelo aprende a predecir varias series objetivo de forma simultánea, capturando relaciones y dependencias tanto dentro de cada serie como entre diferentes series.
Algunas aplicaciones reales son:
Previsión de las ventas de múltiples productos en una tienda online, utilizando los datos históricos de ventas, precios, promociones y otras variables relacionadas con los productos.
Estudio de las emisiones de gases en una turbina de gas, donde se desea predecir la concentración de varios contaminantes (por ejemplo, NOX, CO) a partir de los datos históricos de emisiones y otras variables relevantes.
Modelado conjunto de variables ambientales (por ejemplo, contaminación, temperatura, humedad), donde la evolución de una variable puede influir o estar influida por las demás.
# Creación del modelo
# ==============================================================================
levels = ['o3', 'pm2.5', 'pm10'] # Múltiples series a predecir
lags = 24
model = create_and_compile_model(
series = data, # DataFrame con todas las series (predictores)
levels = levels,
lags = lags,
steps = 24,
recurrent_layer = "LSTM",
recurrent_units = [128, 64],
recurrent_layers_kwargs = {"activation": "tanh"},
dense_units = [64, 32],
compile_kwargs = {'optimizer': Adam(), 'loss': MeanSquaredError()},
model_name = "MultiVariate-MultiOutput-Multi-Step"
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "MultiVariate-MultiOutput-Multi-Step"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 24, 10) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ lstm_1 (LSTM) │ (None, 24, 128) │ 71,168 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ lstm_2 (LSTM) │ (None, 64) │ 49,408 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 64) │ 4,160 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_2 (Dense) │ (None, 32) │ 2,080 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 72) │ 2,376 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 24, 3) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 129,192 (504.66 KB)
Trainable params: 129,192 (504.66 KB)
Non-trainable params: 0 (0.00 B)
# Creación del forecaster
# ==============================================================================
forecaster = ForecasterRnn(
estimator=model,
levels=levels,
lags=lags,
transformer_series=MinMaxScaler(),
fit_kwargs={
"epochs": 25,
"batch_size": 512,
"callbacks": [
EarlyStopping(monitor="val_loss", patience=3, restore_best_weights=True)
],
"series_val": data_val,
}
)
# Fit forecaster
# ==============================================================================
forecaster.fit(data_train)
Using 'torch' backend with device: cuda Epoch 1/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 81ms/step - loss: 0.0572 - val_loss: 0.0232 Epoch 2/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 82ms/step - loss: 0.0173 - val_loss: 0.0104 Epoch 3/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 97ms/step - loss: 0.0121 - val_loss: 0.0097 Epoch 4/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 80ms/step - loss: 0.0114 - val_loss: 0.0092 Epoch 5/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 81ms/step - loss: 0.0107 - val_loss: 0.0086 Epoch 6/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 81ms/step - loss: 0.0100 - val_loss: 0.0076 Epoch 7/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 95ms/step - loss: 0.0090 - val_loss: 0.0067 Epoch 8/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 95ms/step - loss: 0.0084 - val_loss: 0.0065 Epoch 9/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 84ms/step - loss: 0.0081 - val_loss: 0.0063 Epoch 10/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 96ms/step - loss: 0.0078 - val_loss: 0.0062 Epoch 11/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 80ms/step - loss: 0.0077 - val_loss: 0.0062 Epoch 12/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 80ms/step - loss: 0.0075 - val_loss: 0.0061 Epoch 13/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 85ms/step - loss: 0.0073 - val_loss: 0.0061 Epoch 14/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 92ms/step - loss: 0.0072 - val_loss: 0.0059 Epoch 15/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 81ms/step - loss: 0.0071 - val_loss: 0.0059 Epoch 16/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 83ms/step - loss: 0.0070 - val_loss: 0.0058 Epoch 17/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 98ms/step - loss: 0.0069 - val_loss: 0.0058 Epoch 18/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 80ms/step - loss: 0.0068 - val_loss: 0.0058 Epoch 19/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 81ms/step - loss: 0.0067 - val_loss: 0.0057 Epoch 20/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 82ms/step - loss: 0.0066 - val_loss: 0.0057 Epoch 21/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 96ms/step - loss: 0.0066 - val_loss: 0.0057 Epoch 22/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 80ms/step - loss: 0.0064 - val_loss: 0.0057 Epoch 23/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 82ms/step - loss: 0.0063 - val_loss: 0.0056 Epoch 24/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 94ms/step - loss: 0.0062 - val_loss: 0.0059 Epoch 25/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 83ms/step - loss: 0.0062 - val_loss: 0.0057
# Seguimiento del entrenamiento y overfitting
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3))
_ = forecaster.plot_history(ax=ax)
Se pueden hacer predicciones para steps y levels concretos siempre que estén dentro del horizonte de predicción definido por el modelo. Por ejemplo, se puede predecir la concentración de ozono (levels = "o3") para las próximas una y cinco horas (steps = [1, 5]).
# Predicciones para steps y levels específicos
# ==============================================================================
forecaster.predict(steps=[1, 5], levels="o3")
| level | pred | |
|---|---|---|
| 2021-04-01 00:00:00 | o3 | 51.320930 |
| 2021-04-01 04:00:00 | o3 | 40.220501 |
# Predicciones para todos los steps y levels
# ==============================================================================
predictions = forecaster.predict()
predictions
| level | pred | |
|---|---|---|
| 2021-04-01 00:00:00 | o3 | 51.320930 |
| 2021-04-01 00:00:00 | pm2.5 | 12.842420 |
| 2021-04-01 00:00:00 | pm10 | 20.338585 |
| 2021-04-01 01:00:00 | o3 | 50.415470 |
| 2021-04-01 01:00:00 | pm2.5 | 14.436320 |
| ... | ... | ... |
| 2021-04-01 22:00:00 | pm2.5 | 10.209447 |
| 2021-04-01 22:00:00 | pm10 | 17.690262 |
| 2021-04-01 23:00:00 | o3 | 58.094009 |
| 2021-04-01 23:00:00 | pm2.5 | 10.503997 |
| 2021-04-01 23:00:00 | pm10 | 20.092506 |
72 rows × 2 columns
# Backtesting con datos de test
# ==============================================================================
cv = TimeSeriesFold(
steps = forecaster.max_step,
initial_train_size = len(data.loc[:end_validation, :]), # Training + Validation Data
refit = False
)
# Ahora la partición de validación se usa como parte del fit inicial
# Se emplean las epocas identicas en el paso anterior por el early stopping
forecaster.set_fit_kwargs({"epochs": 22,"batch_size": 512})
metrics, predictions = backtesting_forecaster_multiseries(
forecaster = forecaster,
series = data,
cv = cv,
levels = forecaster.levels,
metric = "mean_absolute_error",
suppress_warnings = True,
verbose = False
)
Using 'torch' backend with device: cuda Epoch 1/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 73ms/step - loss: 0.0061 Epoch 2/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 84ms/step - loss: 0.0061 Epoch 3/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 78ms/step - loss: 0.0060 Epoch 4/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 72ms/step - loss: 0.0059 Epoch 5/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 85ms/step - loss: 0.0058 Epoch 6/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 71ms/step - loss: 0.0058 Epoch 7/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 72ms/step - loss: 0.0057 Epoch 8/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 73ms/step - loss: 0.0058 Epoch 9/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 81ms/step - loss: 0.0056 Epoch 10/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 71ms/step - loss: 0.0055 Epoch 11/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 72ms/step - loss: 0.0054 Epoch 12/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 83ms/step - loss: 0.0054 Epoch 13/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 71ms/step - loss: 0.0053 Epoch 14/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 71ms/step - loss: 0.0053 Epoch 15/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 81ms/step - loss: 0.0052 Epoch 16/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 73ms/step - loss: 0.0052 Epoch 17/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 72ms/step - loss: 0.0051 Epoch 18/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 72ms/step - loss: 0.0050 Epoch 19/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 83ms/step - loss: 0.0050 Epoch 20/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 71ms/step - loss: 0.0049 Epoch 21/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 72ms/step - loss: 0.0048 Epoch 22/22 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 83ms/step - loss: 0.0048
0%| | 0/92 [00:00<?, ?it/s]
# Métricas de error de backtesting para cada serie
# ==============================================================================
metric_multivariate_multioutput = metrics.loc[metrics["levels"] == "o3", "mean_absolute_error"].iat[0]
metrics
| levels | mean_absolute_error | |
|---|---|---|
| 0 | o3 | 12.621890 |
| 1 | pm2.5 | 4.363523 |
| 2 | pm10 | 11.673270 |
| 3 | average | 9.552894 |
| 4 | weighted_average | 9.552894 |
| 5 | pooling | 9.552894 |
# Gráfico de las predicciones vs valores reales en el conjunto de test
# =============================================================================
for i, level in enumerate(levels):
fig = go.Figure()
trace1 = go.Scatter(x=data_test.index, y=data_test[level], name="test", mode="lines")
trace2 = go.Scatter(
x=predictions.loc[predictions["level"] == level, "pred"].index,
y=predictions.loc[predictions["level"] == level, "pred"],
name="predictions", mode="lines"
)
fig.add_trace(trace1)
fig.add_trace(trace2)
fig.update_layout(
title="Prediction vs real values in the test set",
xaxis_title="Date time",
yaxis_title=level,
width=800,
height=300,
margin=dict(l=20, r=20, t=35, b=20),
legend=dict(orientation="h", yanchor="top", y=1.05, xanchor="left", x=0)
)
fig.show()
O3: El modelo sigue la tendencia principal y los patrones estacionales, pero suaviza algunos de los picos y valles más extremos.
pm2.5: Las predicciones reflejan los cambios generales, pero el modelo no capta algunos picos repentinos.
pm10: El modelo captura las tendencias generales, pero subestima de forma consistente los picos más altos y los saltos bruscos.
El modelo reproduce el comportamiento principal de cada serie, pero tiende a no captar o suavizar las fluctuaciones más abruptas.
Comparación de estrategias de forecasting¶
Como se ha podido observar, existen diferentes arquitecturas de deep learning y estrategias de modelado que se pueden emplear para predecir series temporales. Como resumen, las estrategias de forecasting se pueden clasificar en:
Serie única, predicción multi-paso: Predecir los valores futuros de una sola serie utilizando solo sus propios valores pasados.
Multivariante, salida única, predicción multi-paso: Utilizar varias series como predictores para pronosticar una serie objetivo a lo largo de varios pasos futuros.
Multivariante, múltiples salidas, predicción multi-paso: Utilizar varias series predictoras para pronosticar varios objetivos a lo largo de varios pasos.
A continuación, se muestra una tabla resumen que compara el Error Absoluto Medio (MAE) de cada enfoque, calculado sobre la misma serie objetivo, "o3":
# Metric comparison
# ==============================================================================
results = {
"Single-Series, Multi-Step": metric_single_series,
"Multi-Series, Single-Output": metric_multivariate,
"Multi-Series, Multi-Output": metric_multivariate_multioutput
}
table_results = pd.DataFrame.from_dict(results, orient='index', columns=['O3 MAE'])
table_results = table_results.style.highlight_min(axis=0, color='green').format(precision=4)
table_results
| O3 MAE | |
|---|---|
| Single-Series, Multi-Step | 11.0835 |
| Multi-Series, Single-Output | 10.8958 |
| Multi-Series, Multi-Output | 12.6219 |
En este ejemplo, los enfoques serie única y multivariante simple producen errores similares, mientras que al añadir más objetivos como salidas (multi-output) el error de predicción aumenta. Sin embargo, no existe una regla universal: la mejor estrategia depende de tus datos, el dominio y los objetivos de la predicción.
Es importante experimentar con diferentes arquitecturas y comparar sus métricas para seleccionar el modelo más adecuado para tu caso de uso concreto.
Variables exógenas en modelos de deep learning¶
Las variables exógenas son predictores externos (como el clima, festivos o eventos especiales) que pueden influir en la serie objetivo, pero que no forman parte de sus propios valores históricos. Al construir modelos de deep learning para predicción de series temporales, incluir estas variables puede ayudar a captar patrones importantes y mejorar la precisión, siempre que sus valores futuros estén disponibles en el momento de la predicción.
En esta sección, mostraremos cómo utilizar variables exógenas en modelos de deep learning con un nuevo conjunto de datos: bike_sharing, que contiene el uso horario de bicicletas en Washington D.C., junto con información meteorológica y de días festivos.
Para saber más sobre variables exógenas en skforecast, visita la guía de usuario de variables exógenas.
# Descargar datos
# ==============================================================================
data_exog = fetch_dataset(name='bike_sharing', raw=False)
data_exog = data_exog[['users', 'temp', 'hum', 'windspeed', 'holiday']]
data_exog = data_exog.loc['2011-04-01 00:00:00':'2012-10-20 23:00:00', :].copy()
data_exog.head(3)
╭───────────────────────────────── bike_sharing ──────────────────────────────────╮ │ Description: │ │ Hourly usage of the bike share system in the city of Washington D.C. during the │ │ years 2011 and 2012. In addition to the number of users per hour, information │ │ about weather conditions and holidays is available. │ │ │ │ Source: │ │ Fanaee-T,Hadi. (2013). Bike Sharing Dataset. UCI Machine Learning Repository. │ │ https://doi.org/10.24432/C5W894. │ │ │ │ URL: │ │ https://raw.githubusercontent.com/skforecast/skforecast- │ │ datasets/main/data/bike_sharing_dataset_clean.csv │ │ │ │ Shape: 17544 rows x 11 columns │ ╰─────────────────────────────────────────────────────────────────────────────────╯
| users | temp | hum | windspeed | holiday | |
|---|---|---|---|---|---|
| date_time | |||||
| 2011-04-01 00:00:00 | 6.0 | 10.66 | 100.0 | 11.0014 | 0.0 |
| 2011-04-01 01:00:00 | 4.0 | 10.66 | 100.0 | 11.0014 | 0.0 |
| 2011-04-01 02:00:00 | 7.0 | 10.66 | 93.0 | 12.9980 | 0.0 |
# Calcular variables de calendario
# ==============================================================================
features_to_extract = [
'month',
'week',
'day_of_week',
'hour'
]
calendar_transformer = DatetimeFeatures(
variables = 'index',
features_to_extract = features_to_extract,
drop_original = False,
)
# Cyclical encoding de las variables de calendario
# ==============================================================================
features_to_encode = [
"month",
"week",
"day_of_week",
"hour",
]
max_values = {
"month": 12,
"week": 52,
"day_of_week": 7,
"hour": 24,
}
cyclical_encoder = CyclicalFeatures(
variables = features_to_encode,
max_values = max_values,
drop_original = True
)
exog_transformer = make_pipeline(
calendar_transformer,
cyclical_encoder
)
data_exog = exog_transformer.fit_transform(data_exog)
exog_features = data_exog.columns.difference(['users']).tolist()
print(f"Exogenous features: {exog_features}")
data_exog.head(3)
Exogenous features: ['day_of_week_cos', 'day_of_week_sin', 'holiday', 'hour_cos', 'hour_sin', 'hum', 'month_cos', 'month_sin', 'temp', 'week_cos', 'week_sin', 'windspeed']
| users | temp | hum | windspeed | holiday | month_sin | month_cos | week_sin | week_cos | day_of_week_sin | day_of_week_cos | hour_sin | hour_cos | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| date_time | |||||||||||||
| 2011-04-01 00:00:00 | 6.0 | 10.66 | 100.0 | 11.0014 | 0.0 | 0.866025 | -0.5 | 1.0 | 6.123234e-17 | -0.433884 | -0.900969 | 0.000000 | 1.000000 |
| 2011-04-01 01:00:00 | 4.0 | 10.66 | 100.0 | 11.0014 | 0.0 | 0.866025 | -0.5 | 1.0 | 6.123234e-17 | -0.433884 | -0.900969 | 0.258819 | 0.965926 |
| 2011-04-01 02:00:00 | 7.0 | 10.66 | 93.0 | 12.9980 | 0.0 | 0.866025 | -0.5 | 1.0 | 6.123234e-17 | -0.433884 | -0.900969 | 0.500000 | 0.866025 |
# Split train-validation-test
# ==============================================================================
end_train = '2012-06-30 23:59:00'
end_validation = '2012-10-01 23:59:00'
data_exog_train = data_exog.loc[: end_train, :]
data_exog_val = data_exog.loc[end_train:end_validation, :]
data_exog_test = data_exog.loc[end_validation:, :]
print(f"Dates train : {data_exog_train.index.min()} --- {data_exog_train.index.max()} (n={len(data_exog_train)})")
print(f"Dates validation : {data_exog_val.index.min()} --- {data_exog_val.index.max()} (n={len(data_exog_val)})")
print(f"Dates test : {data_exog_test.index.min()} --- {data_exog_test.index.max()} (n={len(data_exog_test)})")
Dates train : 2011-04-01 00:00:00 --- 2012-06-30 23:00:00 (n=10968) Dates validation : 2012-07-01 00:00:00 --- 2012-10-01 23:00:00 (n=2232) Dates test : 2012-10-02 00:00:00 --- 2012-10-20 23:00:00 (n=456)
La arquitectura de tu modelo de deep learning debe ser capaz de aceptar entradas adicionales junto con los datos principales de la serie temporal. La función create_and_compile_model lo facilita: basta con pasar las variables exógenas como un DataFrame al argumento exog.
# `create_and_compile_model` con variables exógenas
# ==============================================================================
series = ['users']
levels = ['users']
lags = 72
model = create_and_compile_model(
series = data_exog[series], # Single-series
levels = levels, # Una serie objetivo a predecir
lags = lags,
steps = 36,
exog = data_exog[exog_features], # Variables exógenas
recurrent_layer = "LSTM",
recurrent_units = [128, 64],
recurrent_layers_kwargs = {"activation": "tanh"},
dense_units = [64, 32],
compile_kwargs = {'optimizer': Adam(learning_rate=0.01), 'loss': 'mse'},
model_name = "Single-Series-Multi-Step-Exog"
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "Single-Series-Multi-Step-Exog"
┏━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ Connected to ┃ ┡━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━┩ │ series_input │ (None, 72, 1) │ 0 │ - │ │ (InputLayer) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ lstm_1 (LSTM) │ (None, 72, 128) │ 66,560 │ series_input[0][… │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ lstm_2 (LSTM) │ (None, 64) │ 49,408 │ lstm_1[0][0] │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ repeat_vector │ (None, 36, 64) │ 0 │ lstm_2[0][0] │ │ (RepeatVector) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ exog_input │ (None, 36, 12) │ 0 │ - │ │ (InputLayer) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ concat_exog │ (None, 36, 76) │ 0 │ repeat_vector[0]… │ │ (Concatenate) │ │ │ exog_input[0][0] │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ dense_td_1 │ (None, 36, 64) │ 4,928 │ concat_exog[0][0] │ │ (TimeDistributed) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ dense_td_2 │ (None, 36, 32) │ 2,080 │ dense_td_1[0][0] │ │ (TimeDistributed) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ output_dense_td_la… │ (None, 36, 1) │ 33 │ dense_td_2[0][0] │ │ (TimeDistributed) │ │ │ │ └─────────────────────┴───────────────────┴────────────┴───────────────────┘
Total params: 123,009 (480.50 KB)
Trainable params: 123,009 (480.50 KB)
Non-trainable params: 0 (0.00 B)
# Graficar arquitectura del modelo (requiere `pydot` and `graphviz`)
# ==============================================================================
# from keras.utils import plot_model
# plot_model(model, show_shapes=True, show_layer_names=True, to_file='model-architecture-exog.png')

# Crear el Forecaster
# ==============================================================================
forecaster = ForecasterRnn(
estimator=model,
levels=levels,
lags=lags,
transformer_series=MinMaxScaler(),
transformer_exog=MinMaxScaler(),
fit_kwargs={
"epochs": 25,
"batch_size": 1024,
"callbacks": [
EarlyStopping(monitor="val_loss", patience=3, restore_best_weights=True),
ReduceLROnPlateau(monitor="val_loss", factor=0.5, patience=2, min_lr=1e-5, verbose=1)
], # Callback para detener el entrenamiento cuando ya no esté aprendiendo más y reducir learning rate.
"series_val": data_exog_val[series], # Datos de validación para el entrenamiento del modelo.
"exog_val": data_exog_val[exog_features] # Variables exógenas de validación para el entrenamiento del modelo.
},
)
# Fit forecaster con variables exógenas
# ==============================================================================
forecaster.fit(
series = data_exog_train[series],
exog = data_exog_train[exog_features]
)
Using 'torch' backend with device: cuda Epoch 1/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 261ms/step - loss: 0.1116 - val_loss: 0.0630 - learning_rate: 0.0100 Epoch 2/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 313ms/step - loss: 0.0187 - val_loss: 0.0367 - learning_rate: 0.0100 Epoch 3/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 256ms/step - loss: 0.0155 - val_loss: 0.0349 - learning_rate: 0.0100 Epoch 4/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 255ms/step - loss: 0.0136 - val_loss: 0.0396 - learning_rate: 0.0100 Epoch 5/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 255ms/step - loss: 0.0128 - val_loss: 0.0318 - learning_rate: 0.0100 Epoch 6/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 317ms/step - loss: 0.0109 - val_loss: 0.0272 - learning_rate: 0.0100 Epoch 7/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 256ms/step - loss: 0.0096 - val_loss: 0.0229 - learning_rate: 0.0100 Epoch 8/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 255ms/step - loss: 0.0086 - val_loss: 0.0222 - learning_rate: 0.0100 Epoch 9/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 256ms/step - loss: 0.0087 - val_loss: 0.0232 - learning_rate: 0.0100 Epoch 10/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 4s 353ms/step - loss: 0.0080 - val_loss: 0.0189 - learning_rate: 0.0100 Epoch 11/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 264ms/step - loss: 0.0075 - val_loss: 0.0205 - learning_rate: 0.0100 Epoch 12/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 259ms/step - loss: 0.0071 - val_loss: 0.0164 - learning_rate: 0.0100 Epoch 13/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 257ms/step - loss: 0.0067 - val_loss: 0.0162 - learning_rate: 0.0100 Epoch 14/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 311ms/step - loss: 0.0067 - val_loss: 0.0213 - learning_rate: 0.0100 Epoch 15/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 221ms/step - loss: 0.0078 Epoch 15: ReduceLROnPlateau reducing learning rate to 0.004999999888241291. 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 258ms/step - loss: 0.0078 - val_loss: 0.0164 - learning_rate: 0.0100 Epoch 16/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 257ms/step - loss: 0.0063 - val_loss: 0.0176 - learning_rate: 0.0050
# Visualizar training history
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3))
_ = forecaster.plot_history(ax=ax)
El historial de entrenamiento muestra que, aunque la pérdida de entrenamiento disminuye de forma continua, la pérdida de validación se mantiene más alta y fluctúa entre épocas. Esto sugiere que el modelo probablemente está sobreajustando: aprende bien los datos de entrenamiento, pero tiene dificultades para generalizar a datos nuevos o no vistos. Para corregirlo, puedes probar a añadir regularización (como dropout), simplificar el modelo reduciendo su tamaño o revisar la selección de variables exógenas para mejorar el rendimiento en validación.
Cuando se utilizan variables exógenas, la predicción requiere información adicional sobre los valores futuros de estas variables. Estos datos deben proporcionarse a través del argumento exog en el método predict.
# Predicciones con variables exógenas
# ==============================================================================
predictions = forecaster.predict(exog=data_exog_val[exog_features])
predictions.head(4)
| level | pred | |
|---|---|---|
| 2012-07-01 00:00:00 | users | 117.638023 |
| 2012-07-01 01:00:00 | users | 72.128395 |
| 2012-07-01 02:00:00 | users | 46.112545 |
| 2012-07-01 03:00:00 | users | 24.714808 |
# Backtesting en datos de test con variables exógenas
# ==============================================================================
cv = TimeSeriesFold(
steps = forecaster.max_step,
initial_train_size = len(data_exog.loc[:end_validation, :]), # Training + Validation Data
refit = False
)
# Ahora la partición de validación se usa como parte del fit inicial
# Se emplean las epocas identicas en el paso anterior por el early stopping
forecaster.set_fit_kwargs({"epochs": 19,"batch_size": 1024})
metrics, predictions = backtesting_forecaster_multiseries(
forecaster = forecaster,
series = data_exog[series],
exog = data_exog[exog_features],
cv = cv,
levels = forecaster.levels,
metric = "mean_absolute_error",
suppress_warnings = True,
verbose = False
)
Using 'torch' backend with device: cuda Epoch 1/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 267ms/step - loss: 0.0075 Epoch 2/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 220ms/step - loss: 0.0071 Epoch 3/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 217ms/step - loss: 0.0069 Epoch 4/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 217ms/step - loss: 0.0065 Epoch 5/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 269ms/step - loss: 0.0063 Epoch 6/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 221ms/step - loss: 0.0060 Epoch 7/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 220ms/step - loss: 0.0057 Epoch 8/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 218ms/step - loss: 0.0053 Epoch 9/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 267ms/step - loss: 0.0051 Epoch 10/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 223ms/step - loss: 0.0047 Epoch 11/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 218ms/step - loss: 0.0045 Epoch 12/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 218ms/step - loss: 0.0041 Epoch 13/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 260ms/step - loss: 0.0038 Epoch 14/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 217ms/step - loss: 0.0037 Epoch 15/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 219ms/step - loss: 0.0035 Epoch 16/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 225ms/step - loss: 0.0034 Epoch 17/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 256ms/step - loss: 0.0033 Epoch 18/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 220ms/step - loss: 0.0032 Epoch 19/19 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 222ms/step - loss: 0.0030
0%| | 0/13 [00:00<?, ?it/s]
# Métrica de backtesting
# ==============================================================================
metrics
| levels | mean_absolute_error | |
|---|---|---|
| 0 | users | 51.734275 |
# Predicciones vs valores reales en el conjunto de test
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3))
data_exog_test["users"].plot(ax=ax, label="test")
predictions.loc[predictions["level"] == "users", "pred"].plot(ax=ax, label="predictions")
ax.set_title("users")
ax.legend();
Predicción probabilística con modelos de deep learning¶
Conformal prediction es una metodológia para construir intervalos de predicción que garantizan contener el valor real con una probabilidad especificada (probabilidad de cobertura). Funciona combinando las predicciones de un modelo puntual (point-forecast) con sus residuos pasados, las diferencias entre predicciones previas y los valores reales. Estos residuos ayudan a estimar la incertidumbre de la predicción y a determinar la amplitud del intervalo que se suma a la predicción puntual.
Para saber más sobre conformal predictions en skforecast, visita la guía de usuario Predicción Probabilística: Conformal Prediction.
# Almacenar in-sample residuals
# ==============================================================================
forecaster.set_in_sample_residuals(
series=data_exog_train[series], exog=data_exog_train[exog_features]
)
# Prediction intervals
# ==============================================================================
predictions = forecaster.predict_interval(
steps = None,
exog = data_exog_val.loc[:, exog_features],
interval = [10, 90], # 80% prediction interval
method = 'conformal',
use_in_sample_residuals = True
)
predictions.head(4)
| level | pred | lower_bound | upper_bound | |
|---|---|---|---|---|
| 2012-07-01 00:00:00 | users | 117.638027 | 27.066790 | 208.209264 |
| 2012-07-01 01:00:00 | users | 72.128395 | -18.442843 | 162.699632 |
| 2012-07-01 02:00:00 | users | 46.112546 | -44.458691 | 136.683783 |
| 2012-07-01 03:00:00 | users | 24.714809 | -65.856428 | 115.286046 |
# Plot intervals
# ==============================================================================
plot_prediction_intervals(
predictions = predictions,
y_true = data_exog_val,
target_variable = "users",
title = "Predicted intervals",
kwargs_fill_between = {'color': 'gray', 'alpha': 0.4, 'zorder': 1}
)
Funciones de pérdida personalizadas¶
Por defecto, los modelos Keras en skforecast pueden entrenarse utilizando funciones de pérdida comunes como MeanSquaredError o MeanAbsoluteError. Sin embargo, en muchos problemas de predicción resulta útil diseñar una función de pérdida personalizada (custom loss functions) que refleje los objetivos específicos del problema. Por ejemplo, penalizar más las infraestimaciones que las sobrestimaciones, o ponderar los errores según la magnitud de los valores reales.
Keras y skforecast facilitan este proceso:
Puedes definir una pérdida como una función de Python que recibe los tensores
y_trueyy_predy devuelve un valor escalar.Para garantizar la reproducibilidad y permitir guardar/cargar modelos, estas pérdidas deben registrarse con
@keras.saving.register_keras_serializable().
Esta flexibilidad permite adaptar el proceso de entrenamiento a las necesidades concretas de cada dominio de predicción, asegurando que el modelo optimice en base a las métricas más relevantes para el caso de uso.
# Create custom loss function with tensorflow
# ==============================================================================
# import tensorflow as tf
# @keras.saving.register_keras_serializable(package="custom", name="weighted_mae")
# def weighted_mae(y_true, y_pred):
# error = tf.abs(y_true - y_pred)
# weights = tf.abs(y_true)
# return tf.reduce_mean(error * weights)
# Create custom loss function with pytorch
# ==============================================================================
@keras.saving.register_keras_serializable(package="custom", name="weighted_mae")
def weighted_mae(y_true, y_pred):
"""
Compute weighted mean absolute error.
Args:
y_true (torch.Tensor): Ground truth values.
y_pred (torch.Tensor): Predicted values.
Returns:
torch.Tensor: Weighted MAE loss (scalar).
"""
error = torch.abs(y_true - y_pred)
weights = torch.abs(y_true)
return torch.mean(error * weights)
# `create_and_compile_model` with custom loss function
# ==============================================================================
series = ['users']
levels = ['users']
lags = 72
model = create_and_compile_model(
series = data_exog[series],
levels = levels,
lags = lags,
steps = 36,
exog = data_exog[exog_features],
recurrent_layer = "LSTM",
recurrent_units = [128, 64],
recurrent_layers_kwargs = {"activation": "tanh"},
dense_units = [64, 32],
compile_kwargs = {'optimizer': Adam(learning_rate=0.01), 'loss': weighted_mae}, # Custom loss function
model_name = "Single-Series-Multi-Step-Exog"
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "Single-Series-Multi-Step-Exog"
┏━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ Connected to ┃ ┡━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━┩ │ series_input │ (None, 72, 1) │ 0 │ - │ │ (InputLayer) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ lstm_1 (LSTM) │ (None, 72, 128) │ 66,560 │ series_input[0][… │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ lstm_2 (LSTM) │ (None, 64) │ 49,408 │ lstm_1[0][0] │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ repeat_vector │ (None, 36, 64) │ 0 │ lstm_2[0][0] │ │ (RepeatVector) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ exog_input │ (None, 36, 12) │ 0 │ - │ │ (InputLayer) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ concat_exog │ (None, 36, 76) │ 0 │ repeat_vector[0]… │ │ (Concatenate) │ │ │ exog_input[0][0] │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ dense_td_1 │ (None, 36, 64) │ 4,928 │ concat_exog[0][0] │ │ (TimeDistributed) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ dense_td_2 │ (None, 36, 32) │ 2,080 │ dense_td_1[0][0] │ │ (TimeDistributed) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ output_dense_td_la… │ (None, 36, 1) │ 33 │ dense_td_2[0][0] │ │ (TimeDistributed) │ │ │ │ └─────────────────────┴───────────────────┴────────────┴───────────────────┘
Total params: 123,009 (480.50 KB)
Trainable params: 123,009 (480.50 KB)
Non-trainable params: 0 (0.00 B)
# Forecaster Creation
# ==============================================================================
forecaster = ForecasterRnn(
estimator=model,
levels=levels,
lags=lags,
transformer_series=MinMaxScaler(),
transformer_exog=MinMaxScaler(),
fit_kwargs={
"epochs": 25,
"batch_size": 1024,
"callbacks": [
EarlyStopping(monitor="val_loss", patience=3, restore_best_weights=True),
ReduceLROnPlateau(monitor="val_loss", factor=0.5, patience=2, min_lr=1e-5, verbose=1)
], # Callback to stop training when it is no longer learning and to reduce learning rate.
"series_val": data_exog_val[series], # Validation data for model training.
"exog_val": data_exog_val[exog_features] # Validation data for exogenous variables
},
)
# Fit forecaster with exogenous variables
# ==============================================================================
forecaster.fit(
series = data_exog_train[series],
exog = data_exog_train[exog_features]
)
Using 'torch' backend with device: cuda Epoch 1/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 317ms/step - loss: 0.0507 - val_loss: 0.0635 - learning_rate: 0.0100 Epoch 2/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 261ms/step - loss: 0.0292 - val_loss: 0.0698 - learning_rate: 0.0100 Epoch 3/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 258ms/step - loss: 0.0260 - val_loss: 0.0624 - learning_rate: 0.0100 Epoch 4/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 260ms/step - loss: 0.0234 - val_loss: 0.0577 - learning_rate: 0.0100 Epoch 5/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 313ms/step - loss: 0.0216 - val_loss: 0.0712 - learning_rate: 0.0100 Epoch 6/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 221ms/step - loss: 0.0232 Epoch 6: ReduceLROnPlateau reducing learning rate to 0.004999999888241291. 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 257ms/step - loss: 0.0231 - val_loss: 0.0629 - learning_rate: 0.0100 Epoch 7/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 258ms/step - loss: 0.0197 - val_loss: 0.0513 - learning_rate: 0.0050 Epoch 8/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 260ms/step - loss: 0.0186 - val_loss: 0.0550 - learning_rate: 0.0050 Epoch 9/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 268ms/step - loss: 0.0176 Epoch 9: ReduceLROnPlateau reducing learning rate to 0.0024999999441206455. 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 320ms/step - loss: 0.0176 - val_loss: 0.0533 - learning_rate: 0.0050 Epoch 10/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 271ms/step - loss: 0.0170 - val_loss: 0.0480 - learning_rate: 0.0025 Epoch 11/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 259ms/step - loss: 0.0169 - val_loss: 0.0551 - learning_rate: 0.0025 Epoch 12/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 221ms/step - loss: 0.0170 Epoch 12: ReduceLROnPlateau reducing learning rate to 0.0012499999720603228. 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 258ms/step - loss: 0.0170 - val_loss: 0.0532 - learning_rate: 0.0025 Epoch 13/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 4s 353ms/step - loss: 0.0164 - val_loss: 0.0484 - learning_rate: 0.0012
# Training and overfitting tracking
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3))
_ = forecaster.plot_history(ax=ax)
# Prediction with exogenous variables
# ==============================================================================
predictions = forecaster.predict(exog=data_exog_val[exog_features])
predictions.head(4)
| level | pred | |
|---|---|---|
| 2012-07-01 00:00:00 | users | 78.845116 |
| 2012-07-01 01:00:00 | users | 74.905548 |
| 2012-07-01 02:00:00 | users | 78.467552 |
| 2012-07-01 03:00:00 | users | 87.824837 |
Entendiendo create_and_compile_model en profundidad¶
La función create_and_compile_model está diseñada para simplificar el proceso de construcción y compilación de modelos Keras basados en RNN para predicción de series temporales, tanto con como sin variables exógenas. Esta función permite tanto la creación rápida de prototipos (con valores por defecto razonables) como la personalización avanzada para usuarios expertos.
¿Cómo funciona?
En esencia, create_and_compile_model construye una red neuronal formada por tres bloques principales:
Capas recurrentes (LSTM, GRU o SimpleRNN): Estas capas capturan dependencias temporales en los datos. Puedes controlar el tipo, número y configuración de las capas recurrentes mediante los argumentos
recurrent_layer,recurrent_unitsyrecurrent_layers_kwargs.Capas densas (totalmente conectadas): Tras extraer las características temporales, las capas densas ayudan a modelar relaciones no lineales entre las características aprendidas y el objetivo de predicción. Su estructura se controla con
dense_unitsydense_layers_kwargs.Capa de salida: La última capa densa ajusta el número de objetivos de predicción (
levels) y pasos (steps). Su configuración puede ajustarse medianteoutput_dense_layer_kwargs.
Si incluyes variables exógenas (exog), la función ajusta automáticamente la estructura de entrada para que el modelo reciba tanto la serie temporal principal como las variables adicionales.
Parámetros
series: Datos principales de la serie temporal (como DataFrame), cada columna se trata como una variable de entrada.lags: Número de pasos temporales pasados que se utilizan como predictores. Define la longitud de la secuencia de entrada. El mismo valor debe usarse después en el argumentolagsde ForecasterRnn.steps: Número de pasos futuros a predecir.levels: Lista de variables a predecir (variables objetivo). Puede ser una o varias columnas deseries. Si esNone, se usa por defecto el nombre de las series de entrada.exog: Variables exógenas (opcional), como DataFrame. Deben estar alineadas conseries.recurrent_layer: Tipo de capa recurrente, elige entre'LSTM','GRU'o'RNN'. Keras API: LSTM, GRU, SimpleRNN.recurrent_units: Número de unidades por capa recurrente. Se acepta un solo entero (para una capa) o una lista/tupla para varias capas apiladas.recurrent_layers_kwargs: Diccionario (igual para todas las capas) o lista de diccionarios (uno por capa) con los argumentos para las capas recurrentes correspondientes (por ejemplo, funciones de activación, dropout, etc.).dense_units: Número de unidades por capa densa. Se acepta un solo entero (para una capa) o una lista/tupla para varias capas apiladas.dense_layers_kwargs: Diccionario (igual para todas las capas) o lista de diccionarios (uno por capa) con los argumentos para las capas densas (por ejemplo, funciones de activación, dropout, etc.).output_dense_layer_kwargs: Diccionario con los argumentos para la capa densa de salida (por ejemplo, función de activación, dropout, etc.). Por defecto es{'activation': 'linear'}.compile_kwargs: Diccionario de parámetros para el métodocompile()de Keras, por ejemplo, optimizador, función de pérdida. Por defecto es{'optimizer': Adam(), 'loss': MeanSquaredError()}.model_name: Nombre del modelo.
Consulta la documentación completa de la API para más detalles sobre create_and_compile_model.
Ejemplo: Resumen del modelo y explicación capa por capa (sin exog)¶
# Model summary `create_and_compile_model`
# ==============================================================================
model = create_and_compile_model(
series = data,
levels = ["o3"],
lags = 32,
steps = 24,
recurrent_layer = "GRU",
recurrent_units = 100,
dense_units = 64
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "functional_2"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 32, 10) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ gru_1 (GRU) │ (None, 100) │ 33,600 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 64) │ 6,464 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 24) │ 1,560 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 24, 1) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 41,624 (162.59 KB)
Trainable params: 41,624 (162.59 KB)
Non-trainable params: 0 (0.00 B)
| Nombre de la capa | Tipo | Forma de salida | Paráms. | Descripción |
|---|---|---|---|---|
| series_input | InputLayer |
(None, 32, 10) |
0 | Capa de entrada del modelo. Recibe secuencias de longitud 32 (lags) con 10 variables predictoras por paso temporal. |
| gru_1 | GRU |
(None, 100) |
33,600 | Capa GRU (Gated Recurrent Unit) con 100 unidades y activación 'tanh'. Aprende patrones y dependencias temporales en los datos de entrada. |
| dense_1 | Dense |
(None, 64) |
6,464 | Capa totalmente conectada (dense) con 64 unidades y activación ReLU. Procesa las características extraídas por la capa GRU. |
| output_dense_td_layer | Dense |
(None, 24) |
1,560 | Capa densa de salida con 24 unidades (una por cada uno de los 24 pasos futuros a predecir), activación lineal. |
| reshape | Reshape |
(None, 24, 1) |
0 | Reestructura la salida para ajustarse al formato (steps, variables de salida). Aquí, steps=24 y levels=["o3"], por lo que la salida final es (None, 24, 1). |
Total de parámetros: 41,624 Parámetros entrenables: 41,624 Parámetros no entrenables: 0
Ejemplo: Resumen del modelo y explicación capa por capa (exog)¶
# Crear variables de calendario
# ==============================================================================
data['hour'] = data.index.hour
data['day_of_week'] = data.index.dayofweek
data = pd.get_dummies(
data, columns=['hour', 'day_of_week'], drop_first=True, dtype=float
)
data.head(3)
| so2 | co | no | no2 | pm10 | nox | o3 | veloc. | direc. | pm2.5 | ... | hour_20 | hour_21 | hour_22 | hour_23 | day_of_week_1 | day_of_week_2 | day_of_week_3 | day_of_week_4 | day_of_week_5 | day_of_week_6 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| datetime | |||||||||||||||||||||
| 2019-01-01 00:00:00 | 8.0 | 0.2 | 3.0 | 36.0 | 22.0 | 40.0 | 16.0 | 0.5 | 262.0 | 19.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2019-01-01 01:00:00 | 8.0 | 0.1 | 2.0 | 40.0 | 32.0 | 44.0 | 6.0 | 0.6 | 248.0 | 26.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2019-01-01 02:00:00 | 8.0 | 0.1 | 11.0 | 42.0 | 36.0 | 58.0 | 3.0 | 0.3 | 224.0 | 31.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
3 rows × 39 columns
# Model summary `create_and_compile_model` con variables exógenas
# ==============================================================================
series = ['so2', 'co', 'no', 'no2', 'pm10', 'nox', 'o3', 'veloc.', 'direc.', 'pm2.5']
exog_features = data.columns.difference(series).tolist() # dayofweek_* and hour_*
levels = ['o3', 'pm2.5', 'pm10'] # Múltiples series a predecir
print("Target series:", levels)
print("Series as predictors:", series)
print("Exogenous variables:", exog_features)
print("")
model = create_and_compile_model(
series = data[series],
levels = levels,
lags = 32,
steps = 24,
exog = data[exog_features],
recurrent_layer = "LSTM",
recurrent_units = [128, 64],
recurrent_layers_kwargs = [{'activation': 'tanh'}, {'activation': 'relu'}],
dense_units = [128, 64],
dense_layers_kwargs = {'activation': 'relu'},
output_dense_layer_kwargs = {'activation': 'linear'},
compile_kwargs = {'optimizer': Adam(), 'loss': MeanSquaredError()},
model_name = None
)
model.summary()
Target series: ['o3', 'pm2.5', 'pm10'] Series as predictors: ['so2', 'co', 'no', 'no2', 'pm10', 'nox', 'o3', 'veloc.', 'direc.', 'pm2.5'] Exogenous variables: ['day_of_week_1', 'day_of_week_2', 'day_of_week_3', 'day_of_week_4', 'day_of_week_5', 'day_of_week_6', 'hour_1', 'hour_10', 'hour_11', 'hour_12', 'hour_13', 'hour_14', 'hour_15', 'hour_16', 'hour_17', 'hour_18', 'hour_19', 'hour_2', 'hour_20', 'hour_21', 'hour_22', 'hour_23', 'hour_3', 'hour_4', 'hour_5', 'hour_6', 'hour_7', 'hour_8', 'hour_9'] keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "functional_3"
┏━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ Connected to ┃ ┡━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━┩ │ series_input │ (None, 32, 10) │ 0 │ - │ │ (InputLayer) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ lstm_1 (LSTM) │ (None, 32, 128) │ 71,168 │ series_input[0][… │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ lstm_2 (LSTM) │ (None, 64) │ 49,408 │ lstm_1[0][0] │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ repeat_vector │ (None, 24, 64) │ 0 │ lstm_2[0][0] │ │ (RepeatVector) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ exog_input │ (None, 24, 29) │ 0 │ - │ │ (InputLayer) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ concat_exog │ (None, 24, 93) │ 0 │ repeat_vector[0]… │ │ (Concatenate) │ │ │ exog_input[0][0] │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ dense_td_1 │ (None, 24, 128) │ 12,032 │ concat_exog[0][0] │ │ (TimeDistributed) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ dense_td_2 │ (None, 24, 64) │ 8,256 │ dense_td_1[0][0] │ │ (TimeDistributed) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ output_dense_td_la… │ (None, 24, 3) │ 195 │ dense_td_2[0][0] │ │ (TimeDistributed) │ │ │ │ └─────────────────────┴───────────────────┴────────────┴───────────────────┘
Total params: 141,059 (551.01 KB)
Trainable params: 141,059 (551.01 KB)
Non-trainable params: 0 (0.00 B)
| Nombre de la capa | Tipo | Forma de salida | Paráms. | Descripción |
|---|---|---|---|---|
| series_input | InputLayer |
(None, 32, 10) |
0 | Capa de entrada para la serie temporal principal. Recibe secuencias de 32 pasos temporales (lags) con 10 variables predictoras. |
| lstm_1 | LSTM |
(None, 32, 128) |
71,168 | Primera capa LSTM con 128 unidades y activación 'tanh'. Aprende patrones temporales y dependencias de las secuencias de entrada. |
| lstm_2 | LSTM |
(None, 64) |
49,408 | Segunda capa LSTM con 64 unidades y activación 'relu'. Resuma y condensa la información temporal. |
| repeat_vector | RepeatVector |
(None, 24, 64) |
0 | Repite la salida de la capa LSTM anterior 24 veces, una para cada paso futuro a predecir. |
| exog_input | InputLayer |
(None, 24, 29) |
0 | Capa de entrada para las 29 variables exógenas (características de calendario y hora) para cada uno de los 24 pasos futuros. |
| concat_exog | Concatenate |
(None, 24, 93) |
0 | Concatena la salida repetida de la LSTM y las variables exógenas para cada paso de predicción, uniendo todas las características. |
| dense_td_1 | TimeDistributed (Dense) |
(None, 24, 128) |
12,032 | Capa densa (128 unidades, ReLU) aplicada de forma independiente a cada uno de los 24 pasos, aprendiendo relaciones complejas. |
| dense_td_2 | TimeDistributed (Dense) |
(None, 24, 64) |
8,256 | Segunda capa densa (64 unidades, ReLU), también aplicada a cada paso temporal, procesando aún más las características combinadas. |
| output_dense_td_layer | TimeDistributed (Dense) |
(None, 24, 3) |
195 | Capa de salida final, predice 3 variables objetivo (levels) para cada uno de los 24 pasos futuros (activación 'linear'). |
Total de parámetros: 141,059 Parámetros entrenables: 141,059 Parámetros no entrenables: 0
Ejecutando en GPU¶
skforecast es totalmente compatible con la aceleración por GPU. Si tu ordenador dispone de una GPU compatible y el software adecuado está correctamente instalado, skforecast utilizará automáticamente la GPU para acelerar el entrenamiento.
Consejos para el entrenamiento en GPU
El tamaño del batch es importante: Utilizar batches grandes (por ejemplo, 64, 128, 256 o incluso más) permite que la GPU procese más datos en cada ciclo, haciendo que el entrenamiento sea mucho más rápido que con una CPU. Si el batch es pequeño (por ejemplo, 8 o 16), no se aprovecha toda la potencia de la GPU y la mejora en velocidad puede ser mínima, o incluso inexistente, respecto a la CPU.
Aceleración del rendimiento: En una GPU adecuada, el entrenamiento puede ser varias veces más rápido que en CPU. Por ejemplo, con un batch grande, una NVIDIA T4 GPU puede reducir el tiempo de entrenamiento de más de un minuto (en CPU) a solo unos segundos (en GPU).
Cómo usar la GPU con skforecast
- Instala la versión de PyTorch para GPU (con soporte CUDA). Visita la página de instalación de PyTorch y sigue las instrucciones según tu sistema. Asegúrate de seleccionar la versión que corresponde a tu GPU y versión de CUDA. Por ejemplo, para instalar PyTorch con CUDA 12.6, puedes ejecutar:
pip install torch --index-url https://download.pytorch.org/whl/cu126
- Comprueba si tu GPU está disponible en Python:
# Check if GPU is available
# ==============================================================================
import torch
print("Torch version :", torch.__version__)
print("Cuda available :", torch.cuda.is_available())
print("Device name :", torch.cuda.get_device_name(0) if torch.cuda.is_available() else "CPU")
Torch version : 2.9.0+cu126 Cuda available : True Device name : Tesla T4
- Ejecuta tu código como de costumbre. Si se detecta una GPU, skforecast la utilizará automáticamente.
Cómo extraer matrices de entrenamiento y test¶
Aunque los modelos de predicción suelen emplearse para anticipar valores futuros, es igual de importante entender cómo aprende el modelo a partir de los datos de entrenamiento. Analizar las matrices de entrada y salida utilizadas durante el entrenamiento, las predicciones sobre los datos de entrenamiento o explorar las matrices de predicción es fundamental para evaluar el rendimiento del modelo y detectar áreas de mejora. Este proceso puede revelar si el modelo está sobreajustando, infraajustando o tiene dificultades con ciertos patrones de los datos.
Para saber más sobre cómo extraer matrices de entrenamiento y test, visita la guía de usuario correspondiente.
Conclusiones¶
Gracias a skforecast, aplicar modelos de deep learning a la predicción de series temporales es ahora mucho más sencillo. La librería facilita desde la preparación de los datos hasta la selección y evaluación del modelo, permitiendo crear prototipos, iterar y desplegar modelos potentes sin necesidad de escribir código complejo. Esto permite que tanto principiantes como expertos puedan experimentar con distintas arquitecturas de redes neuronales y encontrar rápidamente el enfoque más adecuado para sus datos y su problema de negocio.
Aspectos clave de esta guía:
Las redes neuronales recurrentes (RNN) son muy flexibles: Se pueden emplear para una amplia variedad de tareas de predicción, desde escenarios simples con una sola serie hasta problemas complejos con múltiples series y salidas.
El rendimiento varía según la complejidad del problema: En configuraciones 1:1 y N:1, el modelo logra menor error, mostrando una buena capacidad para aprender los patrones de la serie temporal. En casos N:M, el error aumenta, probablemente por la mayor complejidad o la menor predictibilidad de algunas series.
La selección y arquitectura del modelo son clave: Conseguir un buen rendimiento con deep learning requiere experimentar con distintas arquitecturas, algo mucho más sencillo y rápido usando skforecast.
La demanda computacional es elevada: Los modelos de deep learning pueden requerir recursos de hardware considerables, especialmente con grandes volúmenes de datos o arquitecturas complejas.
Más series = más contexto, pero no siempre mayor precisión individual: Modelar varias series conjuntamente ayuda a captar las relaciones entre ellas, pero puede reducir la precisión para series individuales.
Las variables exógenas pueden mejorar el rendimiento: Incluir predictores externos relevantes, como el clima o eventos especiales, ayuda a que los modelos capturen influencias reales sobre la serie objetivo.
Información de sesión¶
# Información de la sesión
import session_info
session_info.show(html=False)
----- feature_engine 1.9.3 keras 3.10.0 matplotlib 3.10.0 numpy 2.0.2 pandas 2.2.2 plotly 5.24.1 session_info v1.0.1 skforecast 0.19.0 sklearn 1.6.1 torch 2.9.0+cu126 ----- IPython 7.34.0 jupyter_client 7.4.9 jupyter_core 5.9.1 notebook 6.5.7 ----- Python 3.12.12 (main, Oct 10 2025, 08:52:57) [GCC 11.4.0] Linux-6.6.105+-x86_64-with-glibc2.35 ----- Session information updated at 2025-11-27 11:29
Instrucciones para citar¶
¿Cómo citar este documento?
Si utilizas este documento o alguna parte de él, te agradecemos que lo cites. ¡Muchas gracias!
Deep Learning para la predicción de series temporales: Redes Neuronales Recurrentes (RNN), Gated Recurrent Unit (GRU) y Long Short-Term Memory (LSTM) por Joaquín Amat Rodrigo Fernando Carazo y Javier Escobar Ortiz, disponible bajo licencia Attribution-NonCommercial-ShareAlike 4.0 International en https://www.cienciadedatos.net/documentos/py54-forecasting-con-deep-learning.html
¿Cómo citar skforecast?
Si utilizas skforecast, te agradeceríamos mucho que lo cites. ¡Muchas gracias!
Zenodo:
Amat Rodrigo, Joaquin, & Escobar Ortiz, Javier. (2025). skforecast (v0.19.0). Zenodo. https://doi.org/10.5281/zenodo.8382788
APA:
Amat Rodrigo, J., & Escobar Ortiz, J. (2025). skforecast (Version 0.19.0) [Computer software]. https://doi.org/10.5281/zenodo.8382788
BibTeX:
@software{skforecast, author = {Amat Rodrigo, Joaquin and Escobar Ortiz, Javier}, title = {skforecast}, version = {0.19.0}, month = {11}, year = {2025}, license = {BSD-3-Clause}, url = {https://skforecast.org/}, doi = {10.5281/zenodo.8382788} }
¿Te ha gustado el artículo? Tu ayuda es importante
Tu contribución me ayudará a seguir generando contenido divulgativo gratuito. ¡Muchísimas gracias! 😊
Este documento creado por Joaquín Amat Rodrigo, Fernando Carazo y Javier Escobar Ortiz tiene licencia Attribution-NonCommercial-ShareAlike 4.0 International.
Se permite:
-
Compartir: copiar y redistribuir el material en cualquier medio o formato.
-
Adaptar: remezclar, transformar y crear a partir del material.
Bajo los siguientes términos:
-
Atribución: Debes otorgar el crédito adecuado, proporcionar un enlace a la licencia e indicar si se realizaron cambios. Puedes hacerlo de cualquier manera razonable, pero no de una forma que sugiera que el licenciante te respalda o respalda tu uso.
-
No-Comercial: No puedes utilizar el material para fines comerciales.
-
Compartir-Igual: Si remezclas, transformas o creas a partir del material, debes distribuir tus contribuciones bajo la misma licencia que el original.


