Forecasting probabilístico con machine learning

Más sobre forecasting en: cienciadedatos.net

• Forecasting series temporales con machine learning
• Modelos ARIMA y SARIMAX
• Forecasting series temporales con gradient boosting: XGBoost, LightGBM y CatBoost
• Global Forecasting: Multi-series forecasting
• Forecasting de la demanda eléctrica con machine learning
• Forecasting con deep learning
• Forecasting de visitas a página web con machine learning
• Forecasting del precio de Bitcoin
• Forecasting probabilístico
• Forecasting de demanda intermitente
• Reducir el impacto del Covid en modelos de forecasting
• Modelar series temporales con tendencia utilizando modelos de árboles

Introducción¶

Al tratar de anticipar valores futuros de una serie temporal, la mayoría de los modelos de forecasting intentan predecir cuál será el valor más probable; a esto se le llama point-forecasting. Aunque conocer de antemano el valor esperado de una serie temporal es útil en casi todos los casos de negocio, este tipo de predicción no proporciona información sobre la confianza del modelo ni sobre la incertidumbre de sus predicciones.

El forecasting probabilístico, a diferencia del point-forecasting, es una familia de técnicas que permiten predecir la distribución esperada de la variable respuesta en lugar de un único valor puntual. Este tipo de forecasting proporciona información muy valiosa ya que permite crear intervalos de predicción, es decir, el rango de valores donde es más probable que pueda estar el valor real. Más formalmente, un intervalo de predicción define el intervalo dentro del cual se espera encontrar el verdadero valor de la variable respuesta con una determinada probabilidad.

Skforecast implementa varios métodos para la predicción probabilística:

• Bootstrapped residuals: El bootstrapping es una técnica estadística que permite estimar la distribución de un estadístico al muestrear repetidamente los datos con reemplazo. En el contexto del forecasting, aplicar bootstrapping a los residuos de un modelo permite estimar la distribución de los errores, lo que facilita la construcción de intervalos de predicción.

• Conformal prediction: Conformal prediction es un marco para construir intervalos de predicción que garantizan contener el valor real con una probabilidad determinada (cobertura), bajo la hipótesis de que los datos son intercambiables (exchangeability). En series temporales esta hipótesis solo se cumple de forma aproximada, por lo que la cobertura empírica debe validarse siempre. Se basa en combinar las predicciones puntuales de un modelo de forecasting con sus residuos históricos (diferencias entre predicciones previas y valores observados). Estos residuos permiten estimar la incertidumbre de la predicción y determinar la amplitud del intervalo que se añade en torno a la predicción puntual. Skforecast implementa Split Conformal Prediction (SCP).

  Además, los métodos conformal pueden calibrar intervalos de predicción generados por otras técnicas, como la regresión cuantílica o bootstrapping. En estos casos, el método conformal ajusta los intervalos para garantizar que sigan siendo válidos con respecto a una determinada cobertura.

• Regresión cuantílica (Quantile regression): La regresión cuantílica permite modelar los cuantiles condicionales de una variable respuesta. Al combinar las predicciones de dos modelos de regresión cuantílica, se puede construir un intervalo de predicción en el que cada modelo estima uno de los límites. Por ejemplo, entrenar modelos con $Q = 0.1$ y $Q = 0.9$ produce un intervalo de predicción del 80% ($90\% - 10\% = 80\%$).

Métricas en forecasting probabilístico¶

En el point-forecasting, el modelo genera un único valor para cada paso futuro, y la calidad de las predicciones se evalúa comparando el valor predicho con el valor real de la serie. Ejemplos de métricas utilizadas con este fin son el error absoluto medio (MAE) y la raíz del error cuadrático medio (RMSE).

En el forecasting probabilístico, el modelo no produce un único valor, sino una representación de la distribución de los posibles valores. En la práctica, se trata de una muestra de la distribución (por ejemplo, 150 predicciones obtenidas por bootstrapping) o de un conjunto de cuantiles a partir de los cuales se construyen los intervalos de predicción. La calidad de este tipo de predicciones no puede evaluarse con métricas puntuales. Es necesario evaluar dos propiedades:

• Calibración (calibration): los intervalos contienen el valor real con la frecuencia que promete su nivel nominal. Un intervalo del 80% debería contener en torno al 80% de los valores observados.

• Precisión (sharpness): cómo de estrechos son los intervalos. Para una misma cobertura, los intervalos más estrechos son más informativos.

Existe un compromiso entre ambas propiedades: un intervalo extremadamente amplio siempre alcanza la cobertura nominal, pero no tiene ninguna utilidad. El objetivo es generar intervalos lo más estrechos posible que sigan capturando los valores reales con la probabilidad deseada.

El Winkler score, el WIS y el CRPS son reglas de puntuación propias (proper scoring rules) que combinan calibración y precisión en un único valor, lo que las hace muy útiles para comparar métodos. En este documento, los intervalos se evalúan con la cobertura empírica, el área y el Winkler score.

Bootstrapped Residuals¶

La estimación de intervalos mediante bootstrapping de residuos es un método que permite cuantificar la incertidumbre de las predicciones remuestreando los errores de predicción pasados (residuos). El objetivo es generar intervalos de predicción que capturen la variabilidad del forecast, proporcionando un rango de posibles valores futuros en lugar de una única estimación puntual.

El error en la predicción del siguiente valor de una serie (one-step-ahead forecast) se define como la diferencia entre el valor real y el valor predicho ($e_t = y_t - \hat{y}_{t|t-1}$). Asumiendo que los errores futuros serán similares a los errores pasados, es posible simular diferentes predicciones tomando muestras de los errores vistos en el pasado (es decir, los residuos) y añadiéndolas a las predicciones.

Diagrama del proceso de predicción mediante bootstrapping.

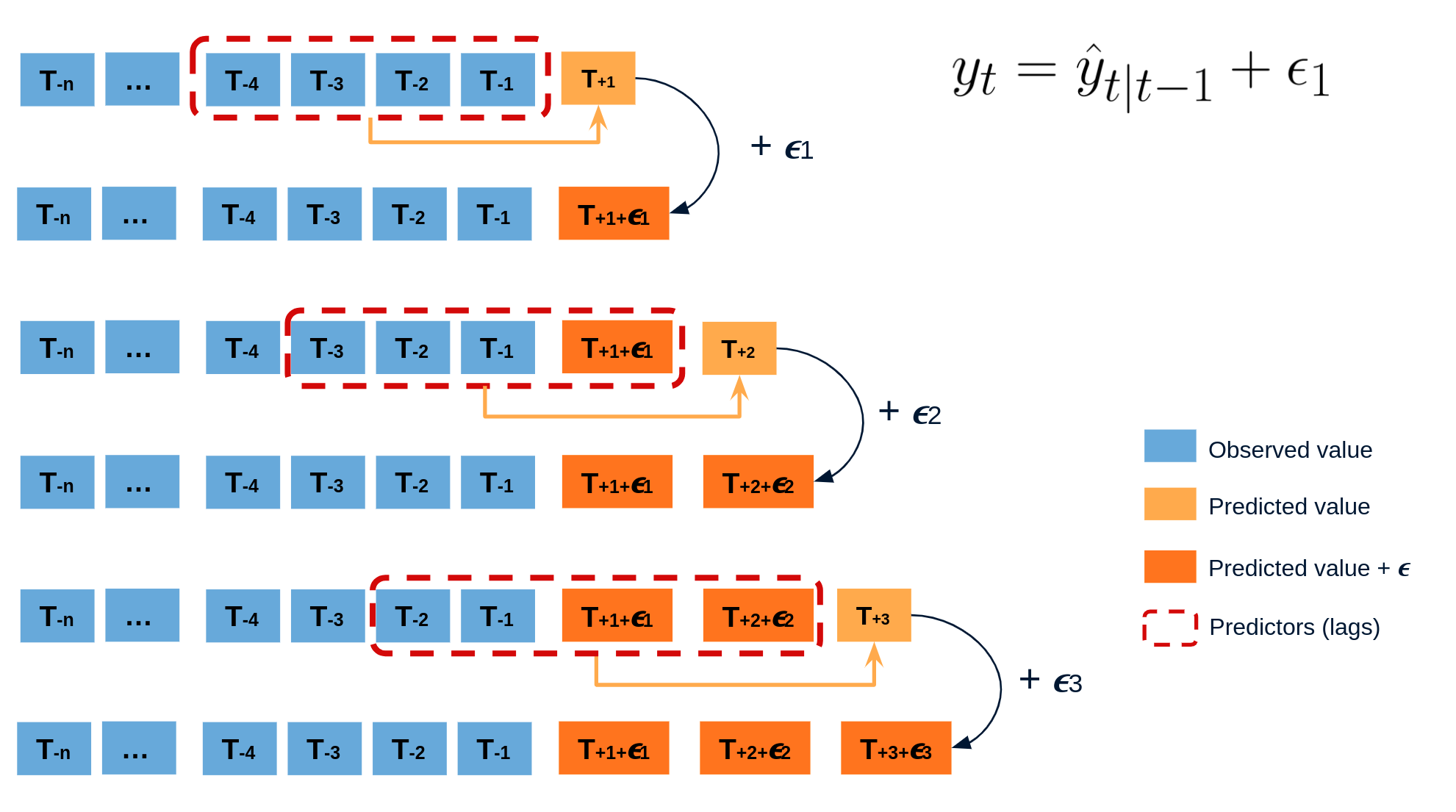
Al repetir este proceso, se crea una colección de predicciones ligeramente diferentes, que representan la distribución de los posibles resultados debida a la varianza esperada en el proceso de forecasting.

Predicciones obtenidas mediante bootstrapping.

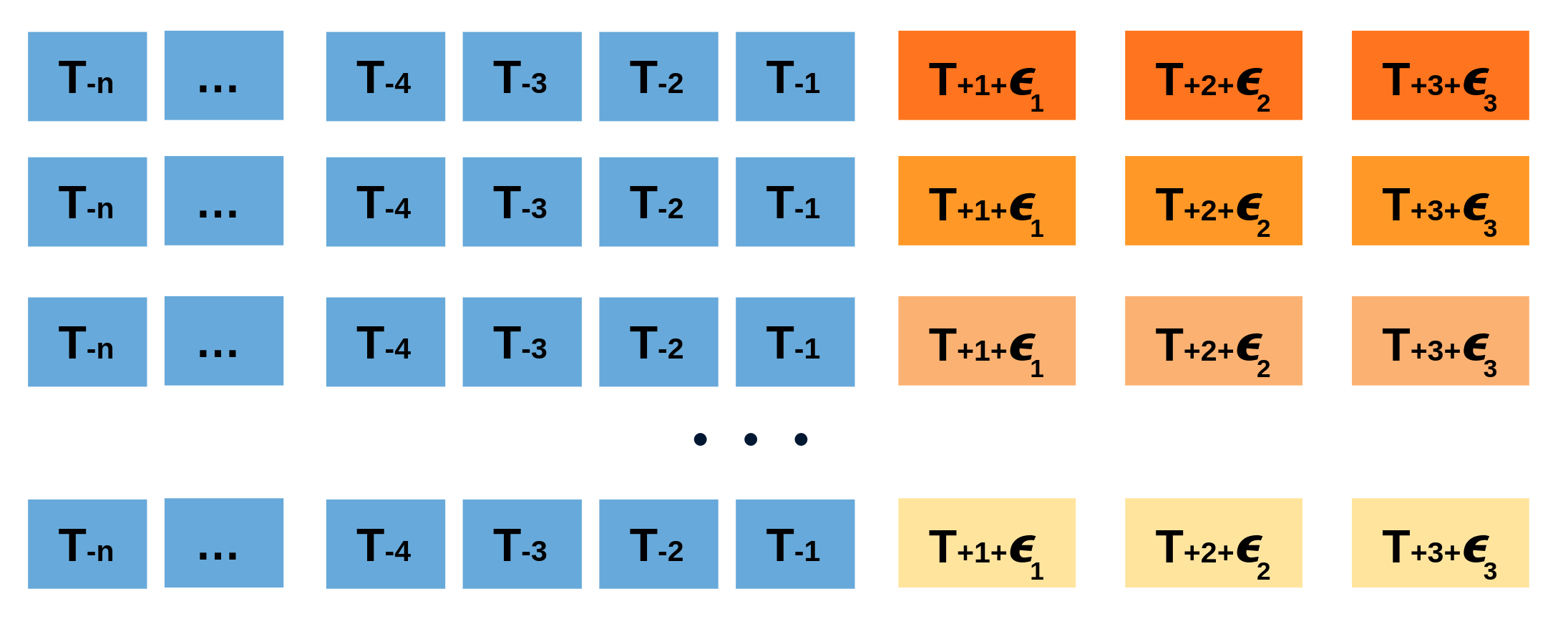
A partir del resultado del proceso de bootstrapping, un intervalo de predicción con una cobertura nominal de $1 - \alpha$ (por ejemplo, $\alpha = 0.2$ para un intervalo del 80%) se obtiene calculando los cuantiles $\alpha/2$ y $1 - \alpha/2$ de las predicciones simuladas en cada horizonte de predicción.

Animación del proceso de predicción probabilística mediante bootstrapping.

Como alternativa, también es posible ajustar una distribución paramétrica para cada horizonte de predicción.

Una de las principales ventajas de esta estrategia es que solo requiere un único modelo para estimar cualquier intervalo. Sin embargo, ejecutar cientos o miles de iteraciones de bootstrapping puede resultar muy costoso desde el punto de vista computacional y no siempre es viable.

Librerías y datos¶

# Preprocesado de datos
# ==============================================================================
import numpy as np
import pandas as pd
from skforecast.datasets import fetch_dataset

# Gráficos
# ==============================================================================
import matplotlib.pyplot as plt
import plotly.graph_objects as go
import plotly.io as pio
import plotly.offline as poff
from skforecast.plot import plot_residuals
pio.templates.default = 'seaborn'
pio.renderers.default = 'notebook'
poff.init_notebook_mode(connected=True)
plt.style.use('seaborn-v0_8-darkgrid')

# Modelado y Forecasting
# ==============================================================================
import skforecast
from lightgbm import LGBMRegressor
from skforecast.recursive import ForecasterRecursive
from skforecast.preprocessing import (
    RollingFeatures,
    CalendarFeatures,
    ConformalIntervalCalibrator
)
from skforecast.model_selection import (
    TimeSeriesFold,
    backtesting_forecaster,
    bayesian_search_forecaster
)
from skforecast.metrics import (
    calculate_coverage,
    winkler_score,
    create_mean_pinball_loss
)

# Configuración
# ==============================================================================
import warnings
from pprint import pprint
warnings.filterwarnings('once')

color = '\033[1m\033[38;5;208m'
print(f'{color}Version skforecast: {skforecast.__version__}')

Version skforecast: 0.25.0

# Descarga de datos
# ==============================================================================
data = fetch_dataset(name='bike_sharing', raw=False)
data = data[['users', 'temp', 'hum', 'windspeed', 'holiday']]
data = data.loc['2011-04-01 00:00:00':'2012-10-20 23:00:00', :].copy()
data.head(3)

╭───────────────────────────────── bike_sharing ──────────────────────────────────╮
│ Description:                                                                    │
│ Hourly usage of the bike share system in the city of Washington D.C. during the │
│ years 2011 and 2012. In addition to the number of users per hour, information   │
│ about weather conditions and holidays is available.                             │
│                                                                                 │
│ Source:                                                                         │
│ Fanaee-T,Hadi. (2013). Bike Sharing Dataset. UCI Machine Learning Repository.   │
│ https://doi.org/10.24432/C5W894.                                                │
│                                                                                 │
│ URL:                                                                            │
│ https://raw.githubusercontent.com/skforecast/skforecast-                        │
│ datasets/main/data/bike_sharing_dataset_clean.csv                               │
│                                                                                 │
│ Shape: 17544 rows x 11 columns                                                  │
╰─────────────────────────────────────────────────────────────────────────────────╯

Se crean variables adicionales a partir de la información del calendario: mes, semana, día de la semana y hora. Estas variables son cíclicas (la hora 23 está tan cerca de la hora 0 como lo está la hora 1), por lo que se codifican con transformaciones seno y coseno que preservan esta continuidad.

El transformador CalendarFeatures se pasa al forecaster a través del argumento calendar_features. De esta forma, las variables de calendario se generan automáticamente a partir del índice temporal tanto en el entrenamiento como en la predicción, y solo es necesario proporcionar el resto de variables exógenas (meteorología y festivos). Para más detalles, consultar la guía de usuario de calendar features.

# Variables de calendario (codificación cíclica)
# ==============================================================================
calendar_transformer = CalendarFeatures(
                           features = ['month', 'week', 'day_of_week', 'hour'],
                           encoding = 'cyclical'
                       )
exog_features = ['holiday', 'hum', 'temp', 'windspeed']

# Vista previa de las variables que el forecaster crea internamente
calendar_transformer.fit_transform(data[['users']]).head(3)

Para facilitar el entrenamiento de los modelos, la búsqueda de hiperparámetros óptimos y la evaluación de su capacidad predictiva, los datos se dividen en tres conjuntos separados: entrenamiento, validación y test.

# Partición de datos en entrenamiento-validación-test
# ==============================================================================
end_train = '2012-06-30 23:59:00'
end_validation = '2012-10-01 23:59:00'
data_train = data.loc[: end_train, :]
data_val   = data.loc[end_train:end_validation, :]
data_test  = data.loc[end_validation:, :]

print(
    f'Fechas train      : {data_train.index.min()} --- {data_train.index.max()}  '
    f'(n={len(data_train)})'
)
print(
    f'Fechas validación : {data_val.index.min()} --- {data_val.index.max()}  '
    f'(n={len(data_val)})'
)
print(
    f'Fechas test       : {data_test.index.min()} --- {data_test.index.max()}  '
    f'(n={len(data_test)})'
)

Fechas train      : 2011-04-01 00:00:00 --- 2012-06-30 23:00:00  (n=10968)
Fechas validación : 2012-07-01 00:00:00 --- 2012-10-01 23:00:00  (n=2232)
Fechas test       : 2012-10-02 00:00:00 --- 2012-10-20 23:00:00  (n=456)

# Gráfico de las particiones
# ==============================================================================
fig = go.Figure()
fig.add_trace(
    go.Scatter(x=data_train.index, y=data_train['users'], mode='lines', name='Train')
)
fig.add_trace(
    go.Scatter(x=data_val.index, y=data_val['users'], mode='lines', name='Validation')
)
fig.add_trace(
    go.Scatter(x=data_test.index, y=data_test['users'], mode='lines', name='Test')
)
fig.update_layout(
    title='Número de usuarios',
    xaxis_title='Fecha',
    yaxis_title='Usuarios',
    width=800,
    height=400,
    margin=dict(l=20, r=20, t=35, b=20),
    legend=dict(orientation='h', yanchor='top', y=1, xanchor='left', x=0.001)
)
fig.show()

Intervalos con residuos in-sample¶

Los intervalos se pueden calcular utilizando los residuos in-sample (residuos del conjunto de entrenamiento), ya sea llamando al método predict_interval(), o realizando un procedimiento completo de backtesting. Sin embargo, esto puede dar lugar a intervalos demasiado estrechos (demasiado optimistas): dado que los residuos se calculan con los mismos datos utilizados para entrenar el modelo, tienden a subestimar el error esperado en datos nuevos.

Se crea un ForecasterRecursive con un regresor LightGBM. Como predictores, utiliza el número de usuarios de las 3 horas anteriores (lags 1, 2 y 3), los valores en torno a la misma hora del día anterior (lags 23, 24 y 25) y de la semana anterior (lags 167, 168 y 169), la media de las últimas 72 horas (RollingFeatures), las variables de calendario y las variables exógenas.

El forecaster se entrena con los datos de entrenamiento y validación. Con store_in_sample_residuals = True, los residuos del proceso de entrenamiento se almacenan en el forecaster.

# Crear y entrenar forecaster
# ==============================================================================
params = {
    'max_depth': 7,
    'n_estimators': 300,
    'learning_rate': 0.06,
    'verbose': -1,
    'random_state': 15926
}
lags = [1, 2, 3, 23, 24, 25, 167, 168, 169]
window_features = RollingFeatures(stats=['mean'], window_sizes=24 * 3)

forecaster = ForecasterRecursive(
                 estimator         = LGBMRegressor(**params),
                 lags              = lags,
                 window_features   = window_features,
                 calendar_features = calendar_transformer
             )

forecaster.fit(
    y    = data.loc[:end_validation, 'users'],
    exog = data.loc[:end_validation, exog_features],
    store_in_sample_residuals = True
)

# Residuos in-sample almacenados durante el entrenamiento
# ==============================================================================
print('Número de residuos almacenados:', len(forecaster.in_sample_residuals_))
forecaster.in_sample_residuals_

Número de residuos almacenados: 10000

array([ 38.2102196 ,  -4.28475005, -29.33611358, ...,  -4.04491958,
       -38.87536687,  -6.27403615], shape=(10000,))

Para limitar el uso de memoria, el forecaster almacena un máximo de 10000 residuos. Si el conjunto de entrenamiento es mayor, como en este caso, se conserva una muestra aleatoria de los residuos.

Se utiliza la función backtesting_forecaster() para estimar los intervalos de predicción de todo el conjunto de test. Los principales argumentos de esta función son:

• use_in_sample_residuals: Si es True, los residuos in-sample se utilizan para calcular los intervalos de predicción. Dado que estos residuos se obtienen del conjunto de entrenamiento, siempre están disponibles, pero suelen dar lugar a intervalos demasiado optimistas. Si es False, se utilizan los residuos out-sample. Estos residuos se obtienen del conjunto de validación y solo están disponibles si se ha llamado al método set_out_sample_residuals(). Se recomienda utilizar los residuos out-sample para lograr la cobertura deseada.

• interval: Los cuantiles utilizados para calcular los intervalos de predicción. Por ejemplo, si se utilizan los percentiles 10 y 90, los intervalos resultantes tienen una cobertura nominal del 80%.

• interval_method: El método utilizado para calcular los intervalos de predicción. Las opciones disponibles son bootstrapping y conformal.

• use_binned_residuals: Si es True, los residuos se seleccionan en función del rango del valor predicho (binned residuals). Esta opción se explica en una sección posterior; por ahora, se establece en False.

• n_boot: El número de muestras bootstrap que se utilizan para estimar los intervalos de predicción cuando interval_method='bootstrapping'. Cuanto mayor sea el número de muestras, más precisos serán los intervalos de predicción, pero mayor será el tiempo de cálculo.

# Backtesting con intervalos de predicción en test usando residuos in-sample
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_validation]))
metric, predictions = backtesting_forecaster(
                          forecaster              = forecaster,
                          y                       = data['users'],
                          exog                    = data[exog_features],
                          cv                      = cv,
                          metric                  = 'mean_absolute_error',
                          interval                = [0.1, 0.9],  # Intervalo del 80%
                          interval_method         = 'bootstrapping',
                          n_boot                  = 150,
                          use_in_sample_residuals = True,  # Residuos in-sample
                          use_binned_residuals    = False
                      )
predictions.head(5)

# Funciones para graficar y evaluar los intervalos de predicción
# ==============================================================================
def plot_predicted_intervals(
    predictions: pd.DataFrame,
    y_true: pd.DataFrame,
    target_variable: str,
    initial_x_zoom: list | None = None,
    title: str | None = None,
    xaxis_title: str | None = None,
    yaxis_title: str | None = None,
):
    """
    Plot predicted intervals vs real values. The point prediction is also
    plotted if `predictions` contains the column 'pred'.

    Parameters
    ----------
    predictions : pandas DataFrame
        Predicted intervals (columns 'lower_bound' and 'upper_bound') and,
        optionally, point predictions (column 'pred').
    y_true : pandas DataFrame
        Real values of target variable.
    target_variable : str
        Name of target variable.
    initial_x_zoom : list, default None
        Initial zoom of x-axis.
    title : str, default None
        Title of the plot.
    xaxis_title : str, default None
        Title of x-axis.
    yaxis_title : str, default None
        Title of y-axis.

    """

    fig = go.Figure()
    if 'pred' in predictions.columns:
        fig.add_trace(
            go.Scatter(
                name='Prediction', x=predictions.index, y=predictions['pred'],
                mode='lines'
            )
        )
    fig.add_trace(
        go.Scatter(
            name='Real value', x=y_true.index, y=y_true[target_variable], mode='lines'
        )
    )
    fig.add_trace(
        go.Scatter(
            name='Upper Bound', x=predictions.index, y=predictions['upper_bound'],
            mode='lines', marker=dict(color='#444'), line=dict(width=0),
            showlegend=False
        )
    )
    fig.add_trace(
        go.Scatter(
            name='Lower Bound', x=predictions.index, y=predictions['lower_bound'],
            mode='lines', marker=dict(color='#444'), line=dict(width=0),
            fillcolor='rgba(68, 68, 68, 0.3)', fill='tonexty', showlegend=False
        )
    )
    fig.update_layout(
        title=title, xaxis_title=xaxis_title, yaxis_title=yaxis_title, width=800,
        height=400, margin=dict(l=20, r=20, t=35, b=20), hovermode='x',
        xaxis=dict(range=initial_x_zoom),
        legend=dict(orientation='h', yanchor='top', y=1.1, xanchor='left', x=0.001)
    )
    fig.show()


def evaluate_predicted_intervals(
    predictions: pd.DataFrame,
    y_true: pd.Series,
    nominal_coverage: float = 0.8,
    verbose: bool = True,
) -> dict:
    """
    Calculate the empirical coverage, the area and the Winkler score of the
    predicted intervals.

    Parameters
    ----------
    predictions : pandas DataFrame
        Predicted intervals (columns 'lower_bound' and 'upper_bound').
    y_true : pandas Series
        Real values of target variable.
    nominal_coverage : float, default 0.8
        Nominal coverage of the intervals. Used to calculate the Winkler score.
    verbose : bool, default True
        Print the results.

    Returns
    -------
    results : dict
        Coverage, area and Winkler score of the intervals.

    """

    coverage = calculate_coverage(
                   y_true      = y_true,
                   lower_bound = predictions['lower_bound'],
                   upper_bound = predictions['upper_bound']
               )
    area = (predictions['upper_bound'] - predictions['lower_bound']).sum()
    winkler = winkler_score(
                  y_true      = y_true,
                  lower_bound = predictions['lower_bound'],
                  upper_bound = predictions['upper_bound'],
                  alpha       = 1 - nominal_coverage
              )
    if verbose:
        print(f'Cobertura del intervalo: {round(100 * coverage, 2)} %')
        print(f'Área del intervalo: {round(area, 2)}')
        print(f'Winkler score: {round(winkler, 2)}')

    return {'coverage': coverage, 'area': area, 'winkler_score': winkler}


def conditional_coverage(
    predictions: pd.DataFrame,
    y_true: pd.Series,
    n_groups: int = 3,
) -> pd.DataFrame:
    """
    Calculate the empirical coverage and the mean width of the predicted
    intervals conditioned on the predicted value. Predictions are divided into
    `n_groups` groups of equal size according to the quantiles of 'pred'.

    Parameters
    ----------
    predictions : pandas DataFrame
        Point predictions (column 'pred') and predicted intervals (columns
        'lower_bound' and 'upper_bound').
    y_true : pandas Series
        Real values of target variable.
    n_groups : int, default 3
        Number of groups.

    Returns
    -------
    results : pandas DataFrame
        Coverage (%) and mean width of the intervals for each group.

    """

    inside = y_true.between(predictions['lower_bound'], predictions['upper_bound'])
    width = predictions['upper_bound'] - predictions['lower_bound']
    groups = pd.qcut(predictions['pred'], q=n_groups, precision=0)
    results = pd.DataFrame({
                  'cobertura (%)': 100 * inside.groupby(groups, observed=True).mean(),
                  'anchura media': width.groupby(groups, observed=True).mean()
              })
    results.index.name = 'Usuarios predichos'

    return results

# Gráfico de intervalos
# ==============================================================================
plot_predicted_intervals(
    predictions     = predictions,
    y_true          = data_test,
    target_variable = 'users',
    xaxis_title     = 'Date time',
    yaxis_title     = 'users',
)

# Cobertura, área y Winkler score de los intervalos (datos de test)
# ==============================================================================
_ = evaluate_predicted_intervals(predictions=predictions, y_true=data_test['users'])

Cobertura del intervalo: 60.75 %
Área del intervalo: 42972.89
Winkler score: 309.76

Los intervalos de predicción presentan un exceso de confianza: tienden a ser demasiado estrechos, lo que da lugar a una cobertura empírica (en torno al 61%) muy inferior a la cobertura nominal (80%). Esto se debe a que los residuos in-sample tienden a sobrestimar la capacidad predictiva del modelo.

# Almacenar las predicciones para su posterior comparación
# ==============================================================================
predictions_in_sample_residuals = predictions.copy()

Residuos Out-sample (no condicionados a los valores predichos)¶

Para evitar el problema de los intervalos demasiado optimistas, es posible utilizar los residuos out-sample (residuos de un conjunto de validación no visto durante el entrenamiento) para estimar los intervalos de predicción. Estos residuos se pueden obtener mediante un proceso de backtesting.

# Backtesting con datos de validación para obtener residuos out-sample
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_train]))
_, predictions_val = backtesting_forecaster(
                         forecaster = forecaster,
                         y          = data.loc[:end_validation, 'users'],
                         exog       = data.loc[:end_validation, exog_features],
                         cv         = cv,
                         metric     = 'mean_absolute_error',
                     )

# Distribución de los residuos out-sample
# ==============================================================================
residuals = data.loc[predictions_val.index, 'users'] - predictions_val['pred']
print(pd.Series(np.where(residuals < 0, 'negativo', 'positivo')).value_counts())
plt.rcParams.update({'font.size': 8})
_ = plot_residuals(residuals=residuals, figsize=(7, 4))

positivo    1281
negativo     951
Name: count, dtype: int64

Los residuos out-sample no están centrados en cero: hay más residuos positivos que negativos, lo que significa que el modelo tiende a subestimar el número de usuarios en el periodo de validación. Dado que el proceso de bootstrapping añade estos residuos a las predicciones, este sesgo se traslada a los intervalos, que quedan desplazados hacia arriba.

Con el método set_out_sample_residuals(), los residuos out-sample se almacenan en el objeto forecaster para que puedan ser utilizados para estimar los intervalos de predicción.

# Almacenar residuos out-sample en el forecaster
# ==============================================================================
forecaster.set_out_sample_residuals(
    y_true = data.loc[predictions_val.index, 'users'],
    y_pred = predictions_val['pred']
)

Ahora que los nuevos residuos se han añadido al forecaster, los intervalos de predicción se pueden calcular utilizando use_in_sample_residuals = False.

# Backtesting con intervalos de predicción en test usando residuos out-sample
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_validation]))
metric, predictions = backtesting_forecaster(
                          forecaster              = forecaster,
                          y                       = data['users'],
                          exog                    = data[exog_features],
                          cv                      = cv,
                          metric                  = 'mean_absolute_error',
                          interval                = [0.1, 0.9],  # Intervalo del 80%
                          interval_method         = 'bootstrapping',
                          n_boot                  = 150,
                          use_in_sample_residuals = False,  # Residuos out-sample
                          use_binned_residuals    = False
                      )
predictions.head(3)

# Gráfico de intervalos
# ==============================================================================
plot_predicted_intervals(
    predictions     = predictions,
    y_true          = data_test,
    target_variable = 'users',
    xaxis_title     = 'Date time',
    yaxis_title     = 'users',
)

# Cobertura, área y Winkler score de los intervalos (datos de test)
# ==============================================================================
_ = evaluate_predicted_intervals(predictions=predictions, y_true=data_test['users'])

Cobertura del intervalo: 83.11 %
Área del intervalo: 100660.88
Winkler score: 311.36

Los intervalos de predicción obtenidos con los residuos out-sample son considerablemente más amplios que los basados en los residuos in-sample, y la cobertura empírica (83.1%) es ahora cercana a la cobertura nominal (80%). Sin embargo, el Winkler score apenas cambia (de 310 a 311): lo que se gana en cobertura se pierde en precisión.

Al examinar el gráfico, se observa que los intervalos tienen una anchura similar independientemente del valor predicho, ya que todos los residuos se muestrean de un único conjunto. Como consecuencia, los intervalos son excesivamente amplios cuando el número de usuarios es bajo (horas nocturnas) y pueden ser demasiado estrechos en los picos de demanda. La siguiente sección muestra cómo hacer que la anchura del intervalo dependa del valor predicho.

# Almacenar las predicciones para su posterior comparación
# ==============================================================================
predictions_out_sample_residuals = predictions.copy()

Intervalos condicionados a los valores predichos (binned residuals)¶

El proceso de bootstrapping asume que los residuos se distribuyen de forma independiente, por lo que pueden utilizarse sin tener en cuenta el valor predicho. En realidad, esto rara vez es cierto; en la mayoría de los casos, la magnitud de los residuos está correlacionada con la magnitud del valor predicho. En este caso, por ejemplo, difícilmente cabría esperar que el error fuera el mismo cuando el número predicho de usuarios es cercano a cero que cuando es de varios cientos.

Para tener en cuenta la dependencia entre los residuos y los valores predichos, skforecast permite agrupar los residuos en K intervalos (bins), donde cada bin está asociado a un rango de valores predichos. Con esta estrategia, el proceso de bootstrapping muestrea los residuos de los diferentes bins en función del valor predicho, lo que puede mejorar la cobertura del intervalo y ajustar su anchura cuando sea necesario, permitiendo que el modelo distribuya mejor la incertidumbre de sus predicciones.

Internamente, skforecast utiliza la clase QuantileBinner para agrupar los datos en bins basados en cuantiles utilizando numpy.percentile. Esta clase es similar a KBinsDiscretizer, pero más rápida para este tipo de agrupación. Los intervalos de los bins se definen siguiendo la convención: bins[i-1] <= x < bins[i]. El proceso de binning se puede ajustar mediante el argumento binner_kwargs del forecaster.

El número de bins es un hiperparámetro. Un número mayor permite que los intervalos se adapten mejor al valor predicho, pero hay menos residuos disponibles en cada bin, por lo que la estimación de los cuantiles es más ruidosa. En este ejemplo se utilizan 15 bins. Si se optimiza el número de bins, debe hacerse con datos de validación, nunca con el conjunto de test.

# Crear y entrenar forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
                 estimator         = LGBMRegressor(**params),
                 lags              = lags,
                 window_features   = window_features,
                 calendar_features = calendar_transformer,
                 binner_kwargs     = {'n_bins': 15}
             )

forecaster.fit(
    y    = data.loc[:end_validation, 'users'],
    exog = data.loc[:end_validation, exog_features],
    store_in_sample_residuals = True
)

Durante el proceso de entrenamiento, el forecaster utiliza las predicciones in-sample para definir los intervalos (bins). Los residuos se asignan a estos bins en función del valor predicho con el que están relacionados (atributo binner_intervals_). Por ejemplo, si el bin "0" tiene un intervalo de (-2.06, 7.34), significa que almacenará los residuos de las predicciones que caigan dentro de ese intervalo.

Cuando se calculan los intervalos de predicción, los residuos se muestrean del bin correspondiente al valor predicho. De esta forma, el modelo puede ajustar la anchura de los intervalos en función del valor predicho, lo que ayuda a distribuir mejor la incertidumbre de las predicciones.

# Intervalos asociados a los bins
# ==============================================================================
pprint(forecaster.binner_intervals_)

{0: (-2.058499067584011, 7.339683335728002),
 1: (7.339683335728002, 15.786737846689995),
 2: (15.786737846689995, 30.53493920944861),
 3: (30.53493920944861, 59.12817141401169),
 4: (59.12817141401169, 90.53042339424537),
 5: (90.53042339424537, 120.3837770378804),
 6: (120.3837770378804, 151.12755002609902),
 7: (151.12755002609902, 178.99957394146344),
 8: (178.99957394146344, 209.83991808145416),
 9: (209.83991808145416, 247.60669961894214),
 10: (247.60669961894214, 289.299070321893),
 11: (289.299070321893, 338.21124164842377),
 12: (338.21124164842377, 415.7439121230614),
 13: (415.7439121230614, 524.3743996547786),
 14: (524.3743996547786, 963.2802014321065)}

El método set_out_sample_residuals() agrupa los residuos según los intervalos aprendidos durante el entrenamiento. Para evitar utilizar demasiada memoria, el número de residuos almacenados por bin se limita a 10_000 // n_bins (666 residuos por bin en este ejemplo).

# Almacenar residuos out-sample en el forecaster
# ==============================================================================
forecaster.set_out_sample_residuals(
    y_true = data.loc[predictions_val.index, 'users'],
    y_pred = predictions_val['pred']
)

# Número de residuos out-sample por bin
# ==============================================================================
for k, v in forecaster.out_sample_residuals_by_bin_.items():
    print(f'Bin {k}: n={len(v)}')

Bin 0: n=62
Bin 1: n=154
Bin 2: n=97
Bin 3: n=153
Bin 4: n=91
Bin 5: n=73
Bin 6: n=95
Bin 7: n=111
Bin 8: n=88
Bin 9: n=163
Bin 10: n=185
Bin 11: n=203
Bin 12: n=199
Bin 13: n=241
Bin 14: n=317

El número de residuos out-sample es muy diferente de un bin a otro. Los bins se definen con los cuantiles de las predicciones in-sample, por lo que contienen el mismo número de residuos in-sample, pero las predicciones del periodo de validación no se reparten uniformemente entre ellos. El bin menos poblado contiene 62 residuos, suficientes para estimar los percentiles 10 y 90, pero ilustra el límite práctico al aumentar el número de bins: cuantos más bins, menos residuos hay disponibles para estimar los cuantiles de cada uno.

# Distribución de los residuos por bin
# ==============================================================================
out_sample_residuals_by_bin_df = pd.DataFrame(
    {k: pd.Series(v) for k, v in forecaster.out_sample_residuals_by_bin_.items()}
)
fig, ax = plt.subplots(figsize=(8, 3))
out_sample_residuals_by_bin_df.boxplot(ax=ax)
ax.set_title('Distribución de los residuos por bin', fontsize=12)
ax.set_xlabel('Bin', fontsize=10)
ax.set_ylabel('Residuos', fontsize=10)
plt.show()

El gráfico de cajas muestra cómo la dispersión y la magnitud de los residuos difieren en función del valor predicho. Los residuos son mayores y más dispersos a medida que el valor predicho aumenta (bin más alto), lo que es consistente con la intuición de que los errores tienden a crecer con la magnitud de las predicciones.

# Resumen de la información de los bins
# ==============================================================================
bins_summary = out_sample_residuals_by_bin_df.describe().T
bins_summary.index.name = 'bin'
bins_summary.insert(0, 'interval', bins_summary.index.map(forecaster.binner_intervals_))
bins_summary['interval'] = bins_summary['interval'].apply(lambda x: np.round(x, 2))
bins_summary

Por último, los intervalos de predicción se estiman de nuevo, esta vez utilizando los residuos out-sample condicionados a los valores predichos.

# Backtesting con intervalos de predicción en test usando residuos out-sample
# condicionados (binned)
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_validation]))
metric, predictions = backtesting_forecaster(
                          forecaster              = forecaster,
                          y                       = data['users'],
                          exog                    = data[exog_features],
                          cv                      = cv,
                          metric                  = 'mean_absolute_error',
                          interval                = [0.1, 0.9],  # Intervalo del 80%
                          interval_method         = 'bootstrapping',
                          n_boot                  = 150,
                          use_in_sample_residuals = False,  # Residuos out-sample
                          use_binned_residuals    = True    # Residuos binned
                      )
predictions.head(3)

# Gráfico de intervalos
# ==============================================================================
plot_predicted_intervals(
    predictions     = predictions,
    y_true          = data_test,
    target_variable = 'users',
    xaxis_title     = 'Date time',
    yaxis_title     = 'users',
)

# Cobertura, área y Winkler score de los intervalos (datos de test)
# ==============================================================================
_ = evaluate_predicted_intervals(predictions=predictions, y_true=data_test['users'])

Cobertura del intervalo: 86.4 %
Área del intervalo: 96776.35
Winkler score: 266.75

Cuando se utilizan residuos out-sample condicionados al valor predicho, la incertidumbre se distribuye de forma diferente: los intervalos son estrechos cuando el número predicho de usuarios es bajo y amplios cuando es alto. En comparación con los residuos out-sample no condicionados, el área se reduce en torno a un 4% (de 100661 a 96776) y el Winkler score mejora de 311 a 267. La cobertura empírica (86.4%) es superior a la cobertura nominal (80%), lo que significa que los intervalos estimados son conservadores.

Una posible razón de este comportamiento conservador es que los residuos out-sample se obtienen con un modelo entrenado únicamente con la partición de entrenamiento, y muestran un sesgo positivo en el periodo de validación. Es de esperar que el modelo final, entrenado con los datos de entrenamiento y validación, tenga errores menores, por lo que estos residuos sobrestiman ligeramente su incertidumbre.

# Almacenar las predicciones para su posterior comparación
# ==============================================================================
predictions_out_sample_residuals_binned = predictions.copy()

El siguiente gráfico compara los intervalos de predicción obtenidos utilizando los residuos in-sample, out-sample y out-sample condicionados a los valores predichos.

# Intervalos con residuos in-sample, out-sample y out-sample binned
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 4))
ax.fill_between(
    predictions_out_sample_residuals.index,
    predictions_out_sample_residuals['lower_bound'],
    predictions_out_sample_residuals['upper_bound'],
    color='gray',
    alpha=0.9,
    label='Out-sample residuals',
    zorder=1
)
ax.fill_between(
    predictions_out_sample_residuals_binned.index,
    predictions_out_sample_residuals_binned['lower_bound'],
    predictions_out_sample_residuals_binned['upper_bound'],
    color='#fc4f30',
    alpha=0.7,
    label='Out-sample binned residuals',
    zorder=2
)
ax.fill_between(
    predictions_in_sample_residuals.index,
    predictions_in_sample_residuals['lower_bound'],
    predictions_in_sample_residuals['upper_bound'],
    color='#30a2da',
    alpha=0.9,
    label='In-sample residuals',
    zorder=3
)
ax.set_xlim(pd.to_datetime(['2012-10-08 00:00:00', '2012-10-15 00:00:00']))
ax.set_title('Intervalos de predicción con diferentes residuos', fontsize=12)
ax.legend();

La cobertura global no lo cuenta todo. Un buen intervalo debe alcanzar la cobertura nominal no solo en promedio, sino también para los distintos niveles de demanda. Para comprobarlo, las predicciones de test se dividen en tres grupos de igual tamaño según el número predicho de usuarios (bajo, medio y alto), y se calcula la cobertura empírica y la anchura media de los intervalos en cada grupo.

# Cobertura y anchura de los intervalos condicionadas al valor predicho
# ==============================================================================
methods = {
    'In-sample residuals': predictions_in_sample_residuals,
    'Out-sample residuals': predictions_out_sample_residuals,
    'Out-sample binned residuals': predictions_out_sample_residuals_binned
}
conditional_results = pd.concat(
    {
        name: conditional_coverage(pred, data_test['users'])
        for name, pred in methods.items()
    },
    axis=1
)
conditional_results.round(1)

La tabla hace explícita la progresión entre las tres aproximaciones:

• Residuos in-sample: la cobertura se desploma a medida que aumenta el valor predicho, del 88.8% en el grupo de predicciones bajas al 36.8% en el grupo de predicciones altas. Los intervalos son demasiado estrechos precisamente donde los errores del modelo son mayores.

• Residuos out-sample: la cobertura global del 83.1% es el promedio de dos errores opuestos. Los intervalos tienen una anchura media de más de 200 usuarios en todos los grupos, lo que resulta excesivo para las predicciones bajas e insuficiente para las altas, donde la cobertura solo alcanza el 67.8%.

• Residuos out-sample condicionados (binned): la cobertura es similar en los tres grupos (83.6%, 88.8% y 86.8%) y la anchura de los intervalos crece con el valor predicho, de 71 a 341 usuarios.

Por lo tanto, utilizar residuos out-sample corrige la calibración global de los intervalos, y condicionarlos al valor predicho corrige dónde se sitúa la incertidumbre.

Predicción de múltiples intervalos¶

La función backtesting_forecaster no solo permite estimar un único intervalo, sino también múltiples cuantiles (percentiles) a partir de los cuales se pueden construir múltiples intervalos de predicción. Esto es útil para evaluar la calidad de los intervalos de predicción para un rango de probabilidades. Además, apenas tiene coste computacional adicional en comparación con la estimación de un solo intervalo.

A continuación, se predicen varios percentiles y, a partir de estos, se crean intervalos de predicción para diferentes niveles de cobertura nominal (10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90% y 95%). Después, se evalúa su cobertura empírica.

# Predicción de múltiples cuantiles
# ==============================================================================
quantiles = [
    0.025, 0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50, 0.55, 0.60,
    0.65, 0.70, 0.75, 0.80, 0.85, 0.90, 0.95, 0.975
]
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_validation]))
metric, predictions = backtesting_forecaster(
                          forecaster              = forecaster,
                          y                       = data['users'],
                          exog                    = data[exog_features],
                          cv                      = cv,
                          metric                  = 'mean_absolute_error',
                          interval                = quantiles,
                          interval_method         = 'bootstrapping',
                          n_boot                  = 150,
                          use_in_sample_residuals = False,  # Residuos out-sample
                          use_binned_residuals    = True    # Residuos binned
                      )
predictions.head()

# Calcular cobertura y área de cada intervalo
# ==============================================================================
intervals = [
    [0.025, 0.975], [0.05, 0.95], [0.10, 0.90], [0.15, 0.85], [0.20, 0.80],
    [0.25, 0.75], [0.30, 0.70], [0.35, 0.65], [0.40, 0.60], [0.45, 0.55]
]
nominal_coverages = [100 * (upper_q - lower_q) for lower_q, upper_q in intervals]
observed_coverages = []
observed_areas = []
for lower_q, upper_q in intervals:
    lower_bound = predictions[f'q_{lower_q}']
    upper_bound = predictions[f'q_{upper_q}']
    observed_coverage = calculate_coverage(
                            y_true      = data_test['users'],
                            lower_bound = lower_bound,
                            upper_bound = upper_bound
                        )
    observed_coverages.append(100 * observed_coverage)
    observed_areas.append((upper_bound - lower_bound).sum())

results = pd.DataFrame({
              'Intervalo': intervals,
              'Cobertura nominal (%)': nominal_coverages,
              'Cobertura observada (%)': observed_coverages,
              'Área': observed_areas
          })
results.round(2)

Para todos los niveles nominales, la cobertura observada es superior a la cobertura nominal (por ejemplo, 86.4% para el intervalo del 80% y 59.9% para el intervalo del 50%). Esto confirma que los intervalos estimados con residuos out-sample condicionados (binned) son conservadores en toda la distribución, no solo para un intervalo concreto. Como es de esperar, el área crece con la cobertura nominal: intervalos más amplios son el precio de capturar una mayor proporción de las observaciones.

Predicción bootstrapping, cuantiles y distribución¶

En las secciones anteriores se ha mostrado el uso del proceso de backtesting para estimar el intervalo de predicción a lo largo de un periodo de tiempo determinado. El objetivo es imitar el comportamiento del modelo en producción ejecutando predicciones a intervalos regulares, actualizando incrementalmente los datos de entrada.

También es posible ejecutar una única predicción que estime N pasos por delante sin pasar por todo el proceso de backtesting. En estos casos, skforecast ofrece cuatro métodos diferentes: predict_bootstrapping, predict_interval, predict_quantiles y predict_dist. Para información detallada sobre estos métodos, consultar la documentación.

Conformal Prediction¶

Conformal prediction es un marco para construir intervalos de predicción que garantizan contener el valor real con una probabilidad determinada (cobertura), bajo la hipótesis de que los datos son intercambiables (exchangeability). En series temporales esta hipótesis solo se cumple de forma aproximada, por lo que la cobertura empírica debe validarse siempre. Se basa en combinar las predicciones puntuales de un modelo de forecasting con sus residuos históricos (diferencias entre predicciones previas y valores observados). Estos residuos permiten estimar la incertidumbre de la predicción y determinar la amplitud del intervalo que se añade en torno a la predicción puntual. Skforecast implementa Split Conformal Prediction (SCP).

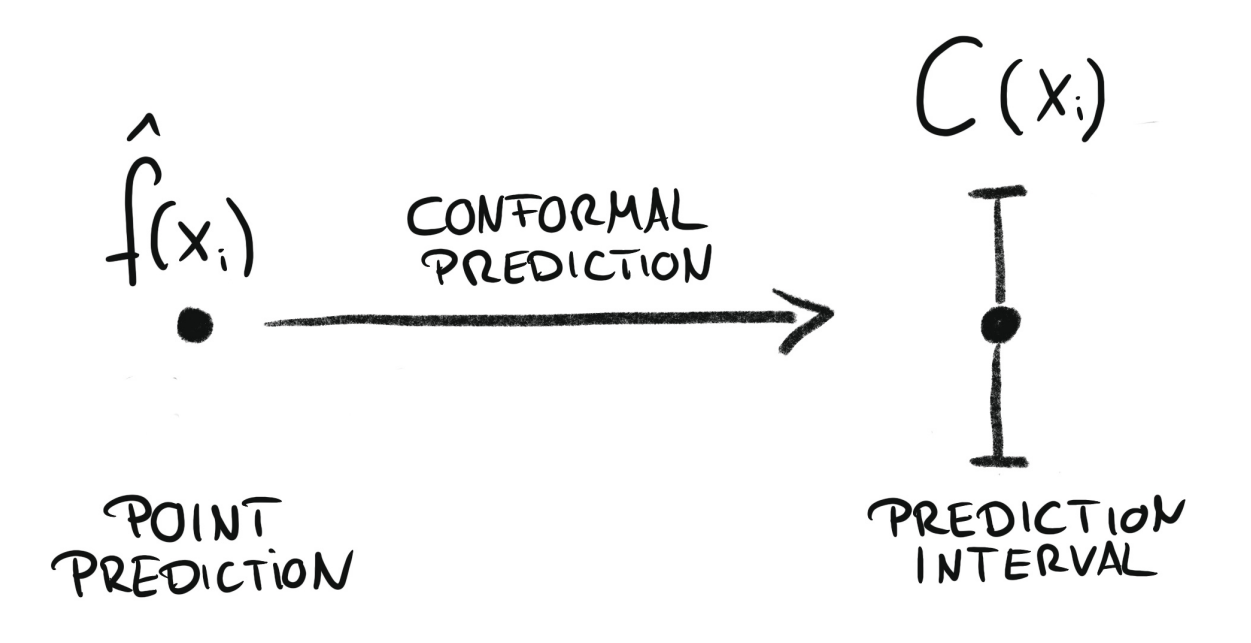
Conformal regression convierte las predicciones puntuales en intervalos de predicción. Fuente: Introduction To Conformal Prediction With Python: A Short Guide For Quantifying Uncertainty Of Machine Learning Models by Christoph Molnar. https://leanpub.com/conformal-prediction

Animación del proceso de predicción conformal probabilística.

Los métodos conformal también pueden calibrar intervalos de predicción generados por otras técnicas, como la regresión cuantílica o el bootstrapping de residuos. En estos casos, el método conformal ajusta los intervalos para garantizar que sigan siendo válidos con respecto a una determinada cobertura. Skforecast proporciona esta funcionalidad a través del transformador ConformalIntervalCalibrator, tal y como se muestra en la última sección de este documento.

Se aplica un proceso de backtesting para estimar los intervalos de predicción del conjunto de test, esta vez utilizando el método conformal. Dado que los residuos out-sample ya están almacenados en el forecaster, el argumento use_in_sample_residuals se establece en False, y use_binned_residuals en True para permitir intervalos adaptativos. Con use_binned_residuals = False, se aplica la misma corrección a todas las predicciones, por lo que los intervalos conformal tienen una anchura constante. Con binned residuals, la anchura se adapta al valor predicho.

# Backtesting con intervalos conformal en test (residuos out-sample binned)
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_validation]))
metric, predictions = backtesting_forecaster(
                          forecaster              = forecaster,
                          y                       = data['users'],
                          exog                    = data[exog_features],
                          cv                      = cv,
                          metric                  = 'mean_absolute_error',
                          interval                = 0.8,  # Intervalo del 80%
                          interval_method         = 'conformal',
                          use_in_sample_residuals = False,  # Residuos out-sample
                          use_binned_residuals    = True    # Conformal adaptativo
                      )

predictions_conformal = predictions.copy()
predictions.head(3)

# Gráfico de intervalos
# ==============================================================================
plot_predicted_intervals(
    predictions     = predictions,
    y_true          = data_test,
    target_variable = 'users',
    xaxis_title     = 'Date time',
    yaxis_title     = 'users',
)

# Cobertura, área y Winkler score de los intervalos (datos de test)
# ==============================================================================
_ = evaluate_predicted_intervals(predictions=predictions, y_true=data_test['users'])

Cobertura del intervalo: 76.75 %
Área del intervalo: 61826.74
Winkler score: 257.98

Los intervalos obtenidos muestran una cobertura empírica (76.8%) ligeramente inferior al 80% nominal, pero cercana a ella. Además, su área (en torno a 61800) es más de un tercio menor que la de los intervalos obtenidos por bootstrapping con residuos out-sample condicionados (en torno a 96800), y alcanzan un Winkler score más bajo (258 frente a 267).

Regresión cuantílica¶

La regresión cuantílica es una técnica que permite estimar los cuantiles condicionales de una variable respuesta. Al combinar las predicciones de dos modelos de regresión cuantílica, es posible construir un intervalo en el que cada modelo estima uno de sus límites. Por ejemplo, los modelos entrenados para $Q = 0.1$ y $Q = 0.9$ generan un intervalo de predicción del 80% ($90\% - 10\% = 80\%$).

Si se utiliza como estimator de un forecaster un algoritmo de machine learning capaz de modelar cuantiles, el método predict devuelve las predicciones del cuantil especificado. Creando dos forecasters, cada uno configurado con un cuantil diferente, sus predicciones se pueden combinar para generar un intervalo de predicción.

A diferencia de la regresión por mínimos cuadrados, que pretende estimar la media condicional de la variable respuesta dados ciertos valores de las variables predictoras, la regresión cuantílica tiene como objetivo estimar los cuantiles condicionales de la variable respuesta. Para una función de distribución continua, el cuantil $\alpha$ $Q_{\alpha}(x)$ se define como el valor tal que la probabilidad de que $Y$ sea menor que $Q_{\alpha}(x)$ es, para un determinado $X=x$, igual a $\alpha$. Por ejemplo, el 36% de los valores de la población son inferiores al cuantil $Q=0.36$. El cuantil más conocido es el cuantil 50%, más comúnmente conocido como mediana.

Existen diversos algoritmos de machine learning capaces de modelar cuantiles. Algunos de ellos son:

• LightGBM

• XGBoost

• CatBoost

• Scikit-learn HistGradientBoostingRegressor

• Scikit-learn QuantileRegressor

• skranger quantile RandomForest

Así como el error cuadrático se utiliza como función de coste para entrenar modelos que predicen el valor medio, se necesita una función de coste específica para entrenar modelos que predicen cuantiles. La función utilizada con más frecuencia para la regresión cuantílica se conoce como quantile loss o pinball loss:

donde $\alpha$ es el cuantil objetivo, $y$ el valor real e $\hat{y}$ la predicción del cuantil. Nótese que aquí $\alpha$ denota el cuantil objetivo (como en el argumento alpha de LightGBM y de create_mean_pinball_loss), no el nivel de no cobertura (miscoverage) utilizado en el Winkler score.

Se puede observar que el coste difiere según el cuantil evaluado. Cuanto mayor sea el cuantil, más se penalizan las subestimaciones y menos las sobreestimaciones. Al igual que ocurre con el MSE y el MAE, el objetivo es minimizar su valor (a menor coste, mejor).

Dos desventajas de la regresión cuantílica en comparación con el método de bootstrapping son que cada cuantil requiere su propio modelo y que la regresión cuantílica no está disponible para todos los tipos de modelos de regresión.

# Crear forecasters: uno para cada límite del intervalo
# ==============================================================================
# Los forecasters obtenidos para alpha=0.1 y alpha=0.9 producen un intervalo de
# predicción del 80% (90% - 10% = 80%).

# Forecaster para el cuantil 10%
forecaster_q10 = ForecasterRecursive(
                     estimator = LGBMRegressor(
                                     objective    = 'quantile',
                                     metric       = 'quantile',
                                     alpha        = 0.1,
                                     random_state = 15926,
                                     verbose      = -1
                                 ),
                     lags              = lags,
                     window_features   = window_features,
                     calendar_features = calendar_transformer
                 )
# Forecaster para el cuantil 90%
forecaster_q90 = ForecasterRecursive(
                     estimator = LGBMRegressor(
                                     objective    = 'quantile',
                                     metric       = 'quantile',
                                     alpha        = 0.9,
                                     random_state = 15926,
                                     verbose      = -1
                                 ),
                     lags              = lags,
                     window_features   = window_features,
                     calendar_features = calendar_transformer
                 )

A continuación, se realiza una búsqueda bayesiana con bayesian_search_forecaster para encontrar los mejores hiperparámetros de los regresores cuantílicos. Al validar un modelo de regresión cuantílica, es importante utilizar una métrica coherente con el cuantil que se está evaluando. En este caso, se utiliza la función de coste pinball. Skforecast proporciona la función create_mean_pinball_loss para calcular la función de coste pinball para un cuantil dado.

Dado que return_best = True por defecto, una vez finalizada la búsqueda, cada forecaster se reentrena con la mejor configuración encontrada.

# Búsqueda bayesiana de hiperparámetros para cada forecaster de cuantiles
# ==============================================================================
def search_space(trial):
    return {
        'n_estimators'  : trial.suggest_int('n_estimators', 100, 500, step=50),
        'max_depth'     : trial.suggest_int('max_depth', 3, 10, step=1),
        'learning_rate' : trial.suggest_float('learning_rate', 0.01, 0.1)
    }

cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_train]))

results_q10, _ = bayesian_search_forecaster(
                     forecaster   = forecaster_q10,
                     y            = data.loc[:end_validation, 'users'],
                     exog         = data.loc[:end_validation, exog_features],
                     cv           = cv,
                     metric       = create_mean_pinball_loss(alpha=0.1),
                     search_space = search_space,
                     n_trials     = 10
                 )

results_q90, _ = bayesian_search_forecaster(
                     forecaster   = forecaster_q90,
                     y            = data.loc[:end_validation, 'users'],
                     exog         = data.loc[:end_validation, exog_features],
                     cv           = cv,
                     metric       = create_mean_pinball_loss(alpha=0.9),
                     search_space = search_space,
                     n_trials     = 10
                 )

print('Mejores resultados para el cuantil 0.1')
display(results_q10.head(3))
print('Mejores resultados para el cuantil 0.9')
display(results_q90.head(3))

Mejores resultados para el cuantil 0.1

Mejores resultados para el cuantil 0.9

Una vez que se han encontrado los mejores hiperparámetros para cada forecaster, se aplica de nuevo un proceso de backtesting utilizando los datos de test.

# Backtesting con datos de test
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_validation]))
metric_q10, predictions_q10 = backtesting_forecaster(
                                  forecaster = forecaster_q10,
                                  y          = data['users'],
                                  exog       = data[exog_features],
                                  cv         = cv,
                                  metric     = create_mean_pinball_loss(alpha=0.1)
                              )

metric_q90, predictions_q90 = backtesting_forecaster(
                                  forecaster = forecaster_q90,
                                  y          = data['users'],
                                  exog       = data[exog_features],
                                  cv         = cv,
                                  metric     = create_mean_pinball_loss(alpha=0.9)
                              )
predictions = pd.DataFrame({
    'lower_bound': predictions_q10['pred'],
    'upper_bound': predictions_q90['pred']
})
predictions_quantile = predictions.copy()
predictions.head(3)

# Gráfico de intervalos
# ==============================================================================
plot_predicted_intervals(
    predictions     = predictions,
    y_true          = data_test,
    target_variable = 'users',
    title           = 'Valor real vs intervalos de predicción en los datos de test',
    xaxis_title     = 'Date time',
    yaxis_title     = 'users',
)

# Cobertura, área y Winkler score de los intervalos (datos de test)
# ==============================================================================
_ = evaluate_predicted_intervals(predictions=predictions, y_true=data_test['users'])

Cobertura del intervalo: 75.88 %
Área del intervalo: 78362.23
Winkler score: 274.59

Los intervalos estimados con regresión cuantílica alcanzan una cobertura empírica del 75.9%, ligeramente inferior al 80% nominal. Tanto su área (en torno a 78400) como su Winkler score (275) se sitúan entre los de conformal prediction y los de bootstrapping con residuos out-sample condicionados.

Comparación de resultados¶

Para seleccionar el método más adecuado para un caso de uso determinado, se deben comparar tanto la cobertura empírica (en qué medida los intervalos capturan el valor real respecto al objetivo nominal del 80%) como la anchura de los intervalos (área). Idealmente, un buen intervalo de predicción es estrecho y, al mismo tiempo, alcanza o supera ligeramente la cobertura nominal. El Winkler score resume ambos aspectos en un único valor (cuanto menor, mejor).

La siguiente tabla muestra las tres métricas para los cinco métodos explorados en este documento.

# Comparación de métodos de forecasting probabilístico
# ==============================================================================
methods = {
    'In-sample residuals': predictions_in_sample_residuals,
    'Out-sample residuals': predictions_out_sample_residuals,
    'Out-sample binned residuals': predictions_out_sample_residuals_binned,
    'Conformal prediction': predictions_conformal,
    'Quantile regression': predictions_quantile
}
comparison = pd.DataFrame({
    name: evaluate_predicted_intervals(pred, data_test['users'], verbose=False)
    for name, pred in methods.items()
}).T
comparison['coverage'] = 100 * comparison['coverage']
comparison.insert(0, 'nominal_coverage', 80.0)
comparison.columns = [
    'Cobertura nominal (%)', 'Cobertura empírica (%)', 'Área', 'Winkler score'
]
comparison.round(2)

De los resultados se pueden extraer varias conclusiones:

• Residuos in-sample: producen los intervalos más estrechos, pero su cobertura (60.8%) es muy inferior al 80% nominal. Muchas observaciones caen fuera de los intervalos, lo que el Winkler score penaliza fuertemente (310).

• Residuos out-sample: corrigen la calibración global (83.1%), pero a costa de intervalos con una anchura similar para todas las predicciones: demasiado amplios cuando el número de usuarios es bajo y demasiado estrechos en los picos de demanda. Por eso el Winkler score no mejora (311) a pesar de la buena cobertura global.

• Residuos out-sample condicionados (binned): corrigen dónde se sitúa la incertidumbre. La cobertura es similar para todos los niveles de demanda, el área es ligeramente menor y el Winkler score mejora (267). Los intervalos son conservadores (86.4%).

• Conformal prediction con binned residuals: alcanza el mejor Winkler score (258), con una cobertura cercana a la nominal (76.8%) y un área más de un tercio menor que la de los intervalos obtenidos por bootstrapping. Además, es el método más rápido, ya que no necesita bootstrapping.

• Regresión cuantílica: da lugar a una cobertura ligeramente inferior a la nominal (75.9%), con un área y un Winkler score intermedios (275). Requiere entrenar un modelo por cuantil y tiene las limitaciones descritas anteriormente para el forecasting recursivo multi-step.

Estos resultados corresponden a una única serie temporal y a un periodo de test de 19 días, por lo que no deben generalizarse: ningún método es el mejor en todos los casos. Como recomendación general, siempre deben preferirse los residuos out-sample a los in-sample, los residuos condicionados al valor predicho (binned) ayudan a situar la incertidumbre donde es necesaria, y la cobertura empírica debe validarse siempre mediante backtesting antes de utilizar los intervalos en producción.

Calibración externa de intervalos de predicción¶

Con frecuencia, los intervalos de predicción obtenidos con los diferentes métodos no logran la cobertura deseada porque son demasiado optimistas o demasiado conservadores. Para abordar este problema, skforecast proporciona el transformador ConformalIntervalCalibrator, que se puede utilizar para calibrar los intervalos de predicción obtenidos con otros métodos.

El ConformalIntervalCalibrator utiliza el método Split Conformal Prediction (SCP) para aprender el factor de corrección necesario para ampliar o reducir los intervalos de predicción, de forma que sean válidos con respecto a una determinada cobertura. El proceso consta de los siguientes pasos:

1. Se estiman los intervalos de predicción de un conjunto de calibración, una partición de los datos no utilizada para entrenar el modelo.

2. A partir de los intervalos predichos y de los valores reales del conjunto de calibración, el transformador aprende el factor de corrección necesario para calibrar estos intervalos.

3. Los intervalos de predicción de nuevos datos (en este ejemplo, el conjunto de test) se ajustan utilizando el factor de corrección aprendido.

Para ilustrar el proceso, los intervalos de predicción del conjunto de test se estiman mediante bootstrapping con residuos in-sample condicionados al valor predicho (binned). Como se ha mostrado anteriormente, los residuos in-sample dan lugar a intervalos con exceso de confianza.

# Backtesting con intervalos de predicción en test usando residuos in-sample
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_validation]))
metric, predictions = backtesting_forecaster(
                          forecaster              = forecaster,
                          y                       = data['users'],
                          exog                    = data[exog_features],
                          cv                      = cv,
                          metric                  = 'mean_absolute_error',
                          interval                = [0.1, 0.9],  # Intervalo del 80%
                          interval_method         = 'bootstrapping',
                          n_boot                  = 150,
                          use_in_sample_residuals = True,  # Residuos in-sample
                          use_binned_residuals    = True   # Residuos binned
                      )

_ = evaluate_predicted_intervals(predictions=predictions, y_true=data_test['users'])

Cobertura del intervalo: 63.6 %
Área del intervalo: 40614.62
Winkler score: 285.95

El mismo procedimiento se aplica al conjunto de validación, que se utiliza como conjunto de calibración. El forecaster se entrena con los datos de entrenamiento y los intervalos del conjunto de validación se predicen mediante backtesting.

# Predecir intervalos para el conjunto de calibración (validación)
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_train]))
_, predictions_cal = backtesting_forecaster(
    forecaster              = forecaster,
    y                       = data.loc[:end_validation, 'users'],
    exog                    = data.loc[:end_validation, exog_features],
    cv                      = cv,
    metric                  = 'mean_absolute_error',
    interval                = [0.1, 0.9],  # Intervalo del 80%
    interval_method         = 'bootstrapping',
    n_boot                  = 150,
    use_in_sample_residuals = True,  # Residuos in-sample
    use_binned_residuals    = True   # Residuos binned
)

# Entrenar un ConformalIntervalCalibrator con el conjunto de calibración
# ==============================================================================
calibrator = ConformalIntervalCalibrator(nominal_coverage=0.8)
calibrator.fit(
    y_true          = data.loc[predictions_cal.index, 'users'],
    y_pred_interval = predictions_cal[['lower_bound', 'upper_bound']]
)
calibrator

El ConformalIntervalCalibrator muestra una cobertura del 63% en el conjunto de calibración, muy por debajo del 80% nominal. En consecuencia, el factor de corrección aprendido es positivo (24.76 usuarios), lo que indica que los intervalos son demasiado estrechos y que ambos límites deben alejarse de la predicción en esa cantidad para alcanzar la cobertura deseada.

A continuación, se calibran los intervalos de predicción del conjunto de test ya calculados.

# Calibrar los intervalos de predicción del conjunto de test
# ==============================================================================
predictions_calibrated = calibrator.transform(
    predictions[['lower_bound', 'upper_bound']]
)

print('Intervalos de predicción antes de la calibración')
print('------------------------------------------------')
display(predictions[['lower_bound', 'upper_bound']].head(3))

print('Intervalos de predicción después de la calibración')
print('--------------------------------------------------')
predictions_calibrated[['lower_bound', 'upper_bound']].head(3)

Intervalos de predicción antes de la calibración
------------------------------------------------

Intervalos de predicción después de la calibración
--------------------------------------------------

# Cobertura, área y Winkler score de los intervalos calibrados (datos de test)
# ==============================================================================
_ = evaluate_predicted_intervals(
        predictions = predictions_calibrated,
        y_true      = data_test['users']
    )

Cobertura del intervalo: 78.73 %
Área del intervalo: 63192.24
Winkler score: 267.7

Tras la calibración, la cobertura empírica de los intervalos en el conjunto de test aumenta del 63.6% al 78.7%, muy cerca de la cobertura nominal del 80%, y el Winkler score mejora de 286 a 268.

Dado que el factor de corrección es un valor constante que se aplica a todos los intervalos, el límite inferior puede tomar valores negativos cuando el número predicho de usuarios es bajo. Si la variable respuesta no puede ser negativa, como en este caso, el límite inferior se puede truncar a cero.

Información de sesión¶

import session_info
session_info.show(html=False)

-----
lightgbm            4.7.0
matplotlib          3.10.9
numpy               2.4.6
pandas              2.3.3
plotly              6.9.0
session_info        v1.0.1
skforecast          0.25.0
-----
IPython             9.15.0
jupyter_client      8.9.1
jupyter_core        5.9.1
-----
Python 3.13.14 | packaged by conda-forge | (main, Jun 12 2026, 09:44:26) [MSC v.1944 64 bit (AMD64)]
Windows-11-10.0.26200-SP0
-----
Session information updated at 2026-09-22 09:43

Instrucciones para citar¶

¿Cómo citar este documento?

Si utilizas este documento o alguna parte de él, te agradecemos que lo cites. ¡Muchas gracias!

Forecasting probabilístico con machine learning por Joaquín Amat Rodrigo y Javier Escobar Ortiz, disponible bajo una licencia Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0 DEED) en https://cienciadedatos.net/documentos/py42-forecasting-probabilistico.html

¿Cómo citar skforecast?

Si utilizas skforecast, te agradecemos mucho que lo cites. ¡Muchas gracias!

Zenodo:

Amat Rodrigo, Joaquin, & Escobar Ortiz, Javier. (2026). skforecast (v0.25.0). Zenodo. https://doi.org/10.5281/zenodo.8382788

APA:

Amat Rodrigo, J., & Escobar Ortiz, J. (2026). skforecast (Version 0.25.0) [Computer software]. https://doi.org/10.5281/zenodo.8382788

BibTeX:

@software{skforecast, author = {Amat Rodrigo, Joaquin and Escobar Ortiz, Javier}, title = {skforecast}, version = {0.25.0}, month = {09}, year = {2026}, license = {BSD-3-Clause}, url = {https://skforecast.org/}, doi = {10.5281/zenodo.8382788} }

¿Te ha gustado el artículo? Tu ayuda es importante

Tu contribución me ayudará a seguir generando contenido divulgativo gratuito. ¡Muchísimas gracias! 😊

Este documento creado por Joaquín Amat Rodrigo y Javier Escobar Ortiz tiene licencia Attribution-NonCommercial-ShareAlike 4.0 International.

Se permite:

• Compartir: copiar y redistribuir el material en cualquier medio o formato.

• Adaptar: remezclar, transformar y crear a partir del material.

Bajo los siguientes términos:

• Atribución: Debes otorgar el crédito adecuado, proporcionar un enlace a la licencia e indicar si se realizaron cambios. Puedes hacerlo de cualquier manera razonable, pero no de una forma que sugiera que el licenciante te respalda o respalda tu uso.

• No-Comercial: No puedes utilizar el material para fines comerciales.

• Compartir-Igual: Si remezclas, transformas o creas a partir del material, debes distribuir tus contribuciones bajo la misma licencia que el original.