Loading [MathJax]/jax/output/SVG/fonts/STIX-Web/fontdata.js
  • Introduction
  • Bootstrapped Residuals
    • Libraries and data
    • Intervals with In-sample residuals
    • Out-sample residuals (non-conditioned on predicted values)
    • Intervals conditioned on predicted values (binned residuals)
    • Prediction of multiple intervals
    • Predict boostrap, interval, quantile and distribution
  • Conformal Prediction
  • Quantile Regression
  • External calibration of prediction intervals
  • Session information
  • Citation


More about forecasting in cienciadedatos.net


Introduction

When trying to predict future values, most forecasting models try to predict what will be the most likely value. This is called point-forecasting. Although knowing the expected value of a time series in advance is useful in almost any business case, this type of prediction does not provide any information about the confidence of the model or the uncertainty of the prediction.

Probabilistic forecasting, as opposed to point-forecasting, is a family of techniques that allow the prediction of the expected distribution of the outcome rather than a single future value. This type of forecasting provides much richer information because it allows the creation of prediction intervals, the range of likely values where the true value may fall. More formally, a prediction interval defines the interval within which the true value of the response variable is expected to be found with a given probability.

Skforecast implements several methods for probabilistic forecasting:

  • Bootstrapped residuals: Bootstrapping is a statistical technique that allows for estimating the distribution of a statistic by resampling the data with replacement. In the context of forecasting, bootstrapping the residuals of a model allows for estimating the distribution of the errors, which can be used to create prediction intervals.

  • Conformal prediction: Conformal prediction is a framework for constructing prediction intervals that are guaranteed to contain the true value with a specified probability (coverage probability). It works by combining the predictions of a point-forecasting model with its past residuals—differences between previous predictions and actual values. These residuals help estimate the uncertainty in the forecast and determine the width of the prediction interval that is then added to the point forecast. Skforecast implements Split Conformal Prediction (SCP).

    Conformal methods can also calibrate prediction intervals generated by other techniques, such as quantile regression or bootstrapped residuals. In this case, the conformal method adjusts the prediction intervals to ensure that they remain valid with respect to the coverage probability.

  • Quantile regression: Quantile regression is a technique for estimating the conditional quantiles of a response variable. By combining the predictions of two quantile regressors, an interval can be constructed, with each model estimating one of the bounds of the interval. For example, models trained on Q=0.1 and Q=0.9 produce an 80% prediction interval (90%−10%=80%).

⚠ Warning

As Rob J Hyndman explains in his blog, in real-world problems, almost all prediction intervals are too narrow. For example, nominal 95% intervals may only provide coverage between 71% and 87%. This is a well-known phenomenon and arises because they do not account for all sources of uncertainty. With forecasting models, there are at least four sources of uncertainty: the random error term, the parameter estimates, the choice of model for the historical data, and the continuation of the historical data generating process into the future. When producing prediction intervals for time series models, generally only the first of these sources is taken into account. Therefore, it is advisable to use test data to validate the empirical coverage of the interval and not only rely on the expected one.

💡 Tip

This is the first in a series of documents on probabilistic forecasting.

Bootstrapped Residuals

Forecasting intervals with bootstrapped residuals is a method used to estimate the uncertainty in predictions by resampling past prediction errors (residuals). The goal is to generate prediction intervals that capture the variability in the forecast, giving a range of possible future values instead of just a single point estimate.

The error of a one-step-ahead forecast is defined as the difference between the actual value and the predicted value (et=yt−ˆyt|t−1). By assuming that future errors will be similar to past errors, it is possible to simulate different predictions by taking samples from the collection of errors previously seen in the past (i.e., the residuals) and adding them to the predictions.


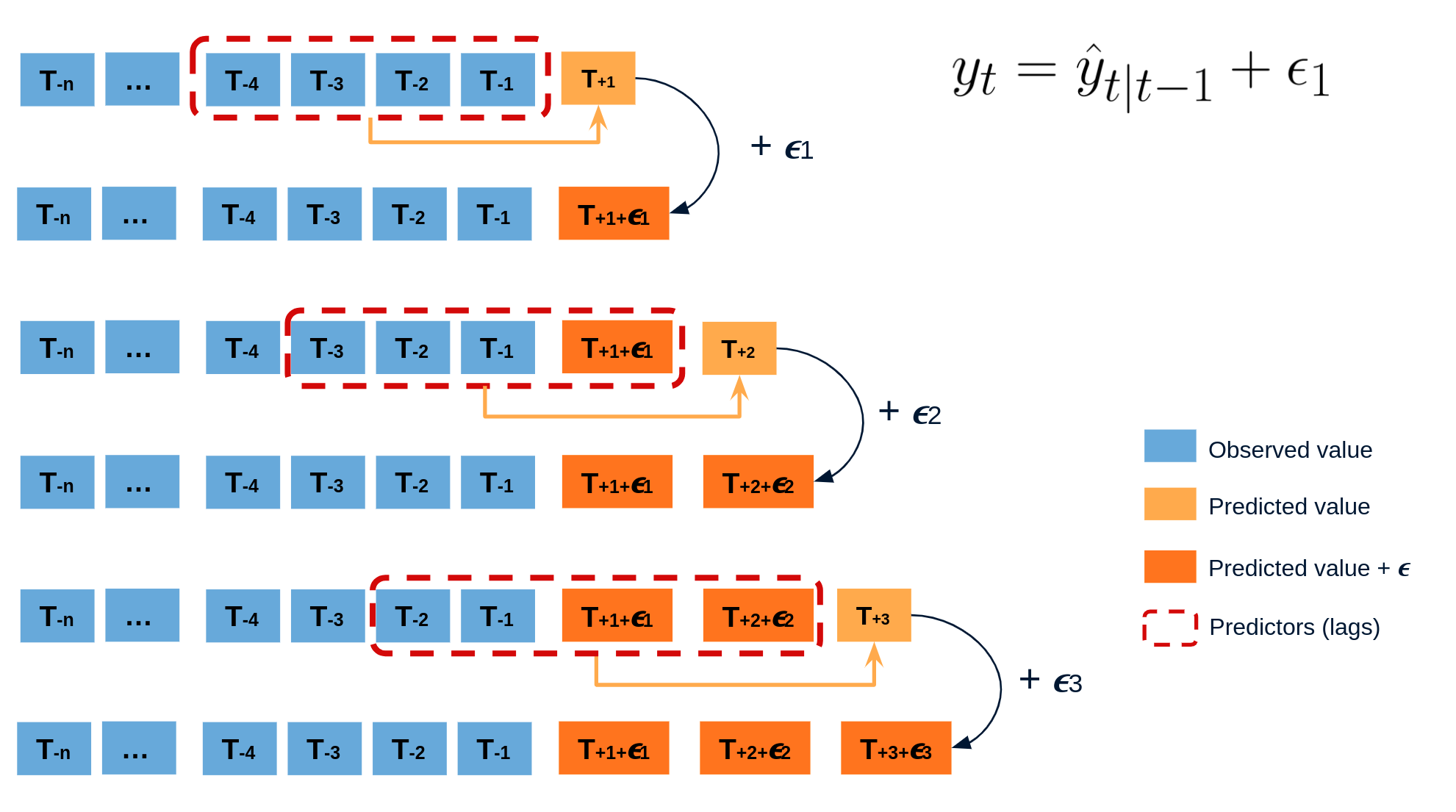
Diagram bootstrapping prediction process.

Repeatedly performing this process creates a collection of slightly different predictions, which represent the distribution of possible outcomes due to the expected variance in the forecasting process.


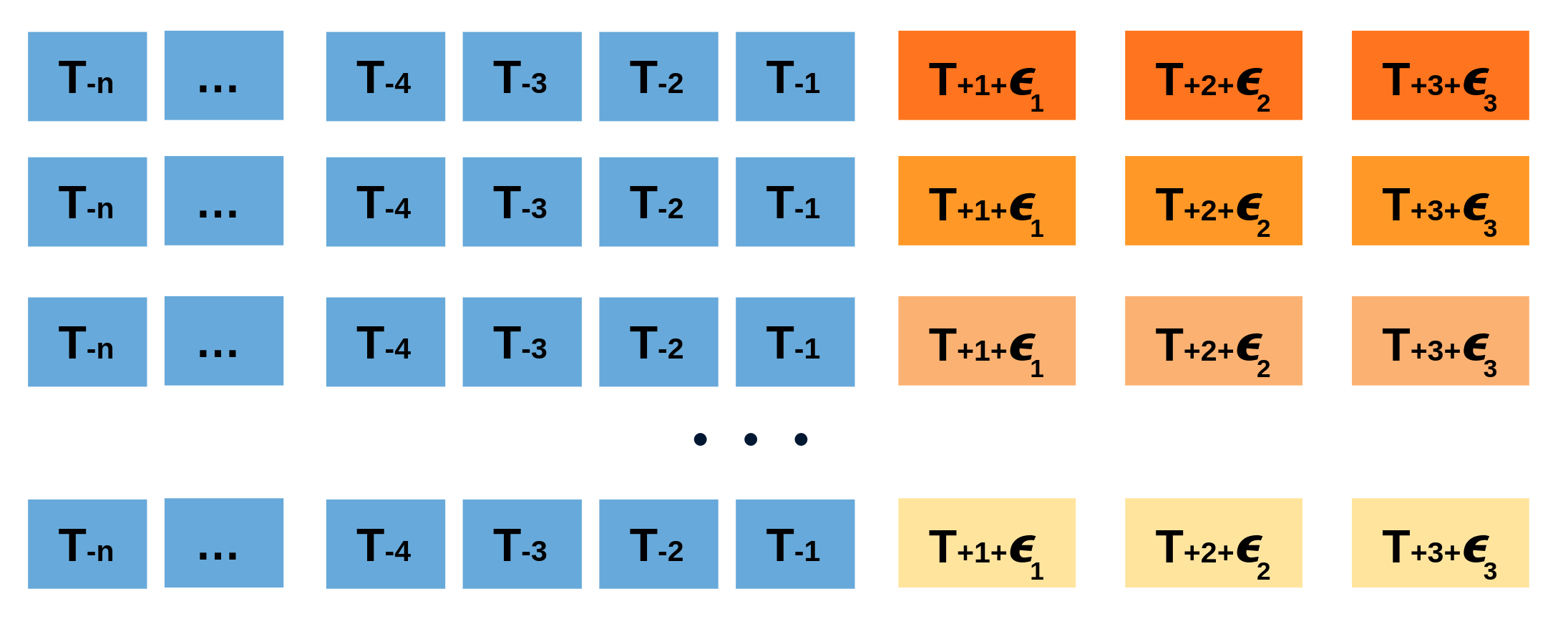
Bootstrapping predictions.

Using the outcome of the bootstrapping process, prediction intervals can be computed by calculating the α/2 and 1−α/2 percentiles at each forecasting horizon.

Alternatively, it is also possible to fit a parametric distribution for each forecast horizon.

One of the main advantages of this strategy is that it requires only a single model to estimate any interval. However, performing hundreds or thousands of bootstrapping iterations can be computationally expensive and may not always be feasible.

Libraries and data

# Data processing
# ==============================================================================
import numpy as np
import pandas as pd
from skforecast.datasets import fetch_dataset

# Plots
# ==============================================================================
import matplotlib.pyplot as plt
import plotly.graph_objects as go
import plotly.io as pio
import plotly.offline as poff
pio.templates.default = "seaborn"
pio.renderers.default = 'notebook' 
poff.init_notebook_mode(connected=True)
plt.style.use('seaborn-v0_8-darkgrid')
from skforecast.plot import plot_residuals
from pprint import pprint

# Modelling and Forecasting
# ==============================================================================
import skforecast
from lightgbm import LGBMRegressor
from sklearn.pipeline import make_pipeline
from feature_engine.datetime import DatetimeFeatures
from feature_engine.creation import CyclicalFeatures
from skforecast.recursive import ForecasterRecursive
from skforecast.direct import ForecasterDirect
from skforecast.preprocessing import RollingFeatures
from skforecast.model_selection import TimeSeriesFold, backtesting_forecaster, bayesian_search_forecaster
from skforecast.metrics import calculate_coverage, create_mean_pinball_loss

# Configuration
# ==============================================================================
import warnings
warnings.filterwarnings('once')

color = '\033[1m\033[38;5;208m'
print(f"{color}Version skforecast: {skforecast.__version__}")

Version skforecast: 0.16.0

# Data download
# ==============================================================================
data = fetch_dataset(name='bike_sharing', raw=False)
data = data[['users', 'temp', 'hum', 'windspeed', 'holiday']]
data = data.loc['2011-04-01 00:00:00':'2012-10-20 23:00:00', :].copy()
data.head(3)

bike_sharing
------------
Hourly usage of the bike share system in the city of Washington D.C. during the
years 2011 and 2012. In addition to the number of users per hour, information
about weather conditions and holidays is available.
Fanaee-T,Hadi. (2013). Bike Sharing Dataset. UCI Machine Learning Repository.
https://doi.org/10.24432/C5W894.
Shape of the dataset: (17544, 11)
users temp hum windspeed holiday
date_time
2011-04-01 00:00:00 6.0 10.66 100.0 11.0014 0.0
2011-04-01 01:00:00 4.0 10.66 100.0 11.0014 0.0
2011-04-01 02:00:00 7.0 10.66 93.0 12.9980 0.0

Additional features are created based on calendar information.

# Calendar features
# ==============================================================================
features_to_extract = ['month', 'week', 'day_of_week', 'hour']
calendar_transformer = DatetimeFeatures(
                        variables           = 'index',
                        features_to_extract = features_to_extract,
                        drop_original       = False,
                     )

# Cliclical encoding of calendar features
# ==============================================================================
features_to_encode = ['month', 'week', 'day_of_week', 'hour']
max_values = {"month": 12, "week": 52, "day_of_week": 7, "hour": 24}
cyclical_encoder = CyclicalFeatures(
                       variables     = features_to_encode,
                       max_values    = max_values,
                       drop_original = True
                   )
exog_transformer = make_pipeline(calendar_transformer, cyclical_encoder)
data = exog_transformer.fit_transform(data)
exog_features = data.columns.difference(['users']).tolist()
data.head(3)
users temp hum windspeed holiday month_sin month_cos week_sin week_cos day_of_week_sin day_of_week_cos hour_sin hour_cos
date_time
2011-04-01 00:00:00 6.0 10.66 100.0 11.0014 0.0 0.866025 -0.5 1.0 6.123234e-17 -0.433884 -0.900969 0.000000 1.000000
2011-04-01 01:00:00 4.0 10.66 100.0 11.0014 0.0 0.866025 -0.5 1.0 6.123234e-17 -0.433884 -0.900969 0.258819 0.965926
2011-04-01 02:00:00 7.0 10.66 93.0 12.9980 0.0 0.866025 -0.5 1.0 6.123234e-17 -0.433884 -0.900969 0.500000 0.866025

To facilitate the training of the models, the search for optimal hyperparameters and the evaluation of their predictive accuracy, the data are divided into three separate sets: training, validation and test.

# Split train-validation-test
# ==============================================================================
end_train = '2012-06-30 23:59:00'
end_validation = '2012-10-01 23:59:00'
data_train = data.loc[: end_train, :]
data_val   = data.loc[end_train:end_validation, :]
data_test  = data.loc[end_validation:, :]

print(f"Dates train      : {data_train.index.min()} --- {data_train.index.max()}  (n={len(data_train)})")
print(f"Dates validacion : {data_val.index.min()} --- {data_val.index.max()}  (n={len(data_val)})")
print(f"Dates test       : {data_test.index.min()} --- {data_test.index.max()}  (n={len(data_test)})")

Dates train      : 2011-04-01 00:00:00 --- 2012-06-30 23:00:00  (n=10968)
Dates validacion : 2012-07-01 00:00:00 --- 2012-10-01 23:00:00  (n=2232)
Dates test       : 2012-10-02 00:00:00 --- 2012-10-20 23:00:00  (n=456)

# Plot partitions
# ==============================================================================
fig = go.Figure()
fig.add_trace(go.Scatter(x=data_train.index, y=data_train['users'], mode='lines', name='Train'))
fig.add_trace(go.Scatter(x=data_val.index, y=data_val['users'], mode='lines', name='Validation'))
fig.add_trace(go.Scatter(x=data_test.index, y=data_test['users'], mode='lines', name='Test'))
fig.update_layout(
    title='Number of users',
    xaxis_title="Time",
    yaxis_title="Users",
    width=800,
    height=400,
    margin=dict(l=20, r=20, t=35, b=20),
    legend=dict(orientation="h", yanchor="top", y=1, xanchor="left", x=0.001
    )
)
fig.show()
May 2011Jul 2011Sep 2011Nov 2011Jan 2012Mar 2012May 2012Jul 2012Sep 201202004006008001000
TrainValidationTestNumber of usersTimeUsers

Intervals with In-sample residuals

Intervals can be computed using in-sample residuals (residuals from the training set), either by calling the predict_interval() method, or by performing a full backtesting procedure. However, this can result in intervals that are too narrow (overly optimistic).

✎ Note

Hiperparametrs used in this example have been previusly optimized using a bayesian search process. For more information about this process, please refer to Hyperparameter tuning and lags selection. 

# Create and fit forecaster
# ==============================================================================
params = {
    "max_depth": 7,
    "n_estimators": 300,
    "learning_rate": 0.06,
    "verbose": -1,
    "random_state": 15926
}
lags = [1, 2, 3, 23, 24, 25, 167, 168, 169]
window_features = RollingFeatures(stats=["mean"], window_sizes=24 * 3)

forecaster = ForecasterRecursive(
                 regressor       = LGBMRegressor(**params),
                 lags            = lags,
                 window_features = window_features,
             )

forecaster.fit(
    y    = data.loc[:end_validation, 'users'],
    exog = data.loc[:end_validation, exog_features],
    store_in_sample_residuals = True
)

# In-sample residuals stored during fit
# ==============================================================================
print("Amount of residuals stored:", len(forecaster.in_sample_residuals_))
forecaster.in_sample_residuals_

Amount of residuals stored: 10000

array([ 42.02327339,  -4.75342728, -39.26777553, ...,  -3.54886809,
       -41.20842177, -13.42207696], shape=(10000,))

The backtesting_forecaster() function is used to estimate the prediction intervals for the entire test set. Few arguments are required to use this function:

  • use_in_sample_residuals: If True, the in-sample residuals are used to compute the prediction intervals. Since these residuals are obtained from the training set, they are always available, but usually lead to overoptimistic intervals. If False, the out-sample residuals are used to calculate the prediction intervals. These residuals are obtained from the validation set and are only available if the set_out_sample_residuals() method has been called. It is recommended to use out-sample residuals to achieve the desired coverage.

  • interval: the quantiles used to calculate the prediction intervals. For example, if the 10th and 90th percentiles are used, the resulting prediction intervals will have a nominal coverage of 80%.

  • interval_method: the method used to calculate the prediction intervals. Available options are bootstraping and conformal.

  • n_boot: the number of bootstrap samples to be used in estimating the prediction intervals when interval_method='bootstraping'. The larger the number of samples, the more accurate the prediction intervals will be, but the longer the calculation will take.

# Backtesting with prediction intervals in test data using in-sample residuals
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_validation]))
metric, predictions = backtesting_forecaster(
                          forecaster              = forecaster,
                          y                       = data['users'],
                          exog                    = data[exog_features],
                          cv                      = cv,
                          metric                  = 'mean_absolute_error',
                          interval                = [10, 90],  # 80% prediction interval
                          interval_method         = 'bootstrapping',
                          n_boot                  = 150,
                          use_in_sample_residuals = True,  # Use in-sample residuals
                          use_binned_residuals    = False,
                      )
predictions.head(5)

  0%|          | 0/19 [00:00<?, ?it/s]
pred lower_bound upper_bound
2012-10-02 00:00:00 58.387527 32.799491 78.248425
2012-10-02 01:00:00 17.870302 -7.253084 50.190172
2012-10-02 02:00:00 7.901576 -17.057776 37.596425
2012-10-02 03:00:00 5.414332 -16.809510 40.194483
2012-10-02 04:00:00 10.379630 -12.696466 56.904041 
# Function to plot predicted intervals
# ======================================================================================
def plot_predicted_intervals(
    predictions: pd.DataFrame,
    y_true: pd.DataFrame,
    target_variable: str,
    initial_x_zoom: list = None,
    title: str = None,
    xaxis_title: str = None,
    yaxis_title: str = None,
):
    """
    Plot predicted intervals vs real values

    Parameters
    ----------
    predictions : pandas DataFrame
        Predicted values and intervals.
    y_true : pandas DataFrame
        Real values of target variable.
    target_variable : str
        Name of target variable.
    initial_x_zoom : list, default `None`
        Initial zoom of x-axis, by default None.
    title : str, default `None`
        Title of the plot, by default None.
    xaxis_title : str, default `None`
        Title of x-axis, by default None.
    yaxis_title : str, default `None`
        Title of y-axis, by default None.
    
    """

    fig = go.Figure([
        go.Scatter(name='Prediction', x=predictions.index, y=predictions['pred'], mode='lines'),
        go.Scatter(name='Real value', x=y_true.index, y=y_true[target_variable], mode='lines'),
        go.Scatter(
            name='Upper Bound', x=predictions.index, y=predictions['upper_bound'],
            mode='lines', marker=dict(color="#444"), line=dict(width=0), showlegend=False
        ),
        go.Scatter(
            name='Lower Bound', x=predictions.index, y=predictions['lower_bound'],
            marker=dict(color="#444"), line=dict(width=0), mode='lines',
            fillcolor='rgba(68, 68, 68, 0.3)', fill='tonexty', showlegend=False
        )
    ])
    fig.update_layout(
        title=title, xaxis_title=xaxis_title, yaxis_title=yaxis_title, width=800,
        height=400, margin=dict(l=20, r=20, t=35, b=20), hovermode="x",
        xaxis=dict(range=initial_x_zoom),
        legend=dict(orientation="h", yanchor="top", y=1.1, xanchor="left", x=0.001)
    )
    fig.show()

# Plot intervals
# ==============================================================================
plot_predicted_intervals(
    predictions     = predictions,
    y_true          = data_test,
    target_variable = "users",
    xaxis_title     = "Date time",
    yaxis_title     = "users",
)

# Coverage (on test data)
# ==============================================================================
coverage = calculate_coverage(
               y_true      = data.loc[end_validation:, 'users'],
               lower_bound = predictions["lower_bound"], 
               upper_bound = predictions["upper_bound"]
           )
print(f"Predicted interval coverage: {round(100 * coverage, 2)} %")

# Area of the interval
# ==============================================================================
area = (predictions["upper_bound"] - predictions["lower_bound"]).sum()
print(f"Area of the interval: {round(area, 2)}")
Oct 32012Oct 5Oct 7Oct 9Oct 11Oct 13Oct 15Oct 17Oct 1902004006008001000
Real valuePredictionDate timeusers
Predicted interval coverage: 61.84 %
Area of the interval: 43177.89

The prediction intervals exhibit overconfidence as they tend to be excessively narrow, resulting in a true coverage that falls below the nominal coverage. This phenomenon arises from the tendency of in-sample residuals to often overestimate the predictive capacity of the model.

# Store results for later comparison
# ==============================================================================
predictions_in_sample_residuals = predictions.copy()

Out-sample residuals (non-conditioned on predicted values)

To address the issue of overoptimistic intervals, it is possible to use out-sample residuals (residuals from a validation set not seen during training) to estimate the prediction intervals. These residuals can be obtained through backtesting.

# Backtesting on validation data to obtain out-sample residuals
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_train]))
_, predictions_val = backtesting_forecaster(
                         forecaster    = forecaster,
                         y             = data.loc[:end_validation, 'users'],
                         exog          = data.loc[:end_validation, exog_features],
                         cv            = cv,
                         metric        = 'mean_absolute_error',
                     )

  0%|          | 0/93 [00:00<?, ?it/s]
# Out-sample residuals distribution
# ==============================================================================
residuals = data.loc[predictions_val.index, 'users'] - predictions_val['pred']
print(pd.Series(np.where(residuals < 0, 'negative', 'positive')).value_counts())
plt.rcParams.update({'font.size': 8})
_ = plot_residuals(residuals=residuals, figsize=(7, 4))

positive    1297
negative     935
Name: count, dtype: int64

With the set_out_sample_residuals() method, the out-sample residuals are stored in the forecaster object so that they can be used to calibrate the prediction intervals.

# Store out-sample residuals in the forecaster
# ==============================================================================
forecaster.set_out_sample_residuals(
    y_true = data.loc[predictions_val.index, 'users'], 
    y_pred = predictions_val['pred']
)

Now that the new residuals have been added to the forecaster, the prediction intervals can be calculated using use_in_sample_residuals = False.

# Backtesting with prediction intervals in test data using out-sample residuals
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_validation]))
metric, predictions = backtesting_forecaster(
                          forecaster              = forecaster,
                          y                       = data['users'],
                          exog                    = data[exog_features],
                          cv                      = cv,
                          metric                  = 'mean_absolute_error',
                          interval                = [10, 90],  # 80% prediction interval
                          interval_method         = 'bootstrapping',
                          n_boot                  = 150,
                          use_in_sample_residuals = False,  # Use out-sample residuals
                          use_binned_residuals    = False,
                      )
predictions.head(3)

  0%|          | 0/19 [00:00<?, ?it/s]
pred lower_bound upper_bound
2012-10-02 00:00:00 58.387527 30.961801 133.296285
2012-10-02 01:00:00 17.870302 -14.031592 132.635745
2012-10-02 02:00:00 7.901576 -32.265023 142.360525 
# Plot intervals
# ==============================================================================
plot_predicted_intervals(
    predictions     = predictions,
    y_true          = data_test,
    target_variable = "users",
    xaxis_title     = "Date time",
    yaxis_title     = "users",
)

# Predicted interval coverage (on test data)
# ==============================================================================
coverage = calculate_coverage(
               y_true      = data.loc[end_validation:, 'users'],
               lower_bound = predictions["lower_bound"], 
               upper_bound = predictions["upper_bound"]
           )
print(f"Predicted interval coverage: {round(100 * coverage, 2)} %")

# Area of the interval
# ==============================================================================
area = (predictions["upper_bound"] - predictions["lower_bound"]).sum()
print(f"Area of the interval: {round(area, 2)}")
Oct 32012Oct 5Oct 7Oct 9Oct 11Oct 13Oct 15Oct 17Oct 1902004006008001000
Real valuePredictionDate timeusers
Predicted interval coverage: 83.33 %
Area of the interval: 101257.22

The prediction intervals derived from the out-of-sample residuals are considerably wider than those based on the in-sample residuals, resulting in an empirical coverage closer to the nominal coverage. Looking at the plot, it's clear that the intervals are particularly wide at low predicted values, suggesting that the model struggles to accurately capture the uncertainty in its predictions at these lower values.

# Store results for later comparison
# ==============================================================================
predictions_out_sample_residuals = predictions.copy()

Intervals conditioned on predicted values (binned residuals)

The bootstrapping process assumes that the residuals are independently distributed so that they can be used independently of the predicted value. In reality, this is rarely true; in most cases, the magnitude of the residuals is correlated with the magnitude of the predicted value. In this case, for example, one would hardly expect the error to be the same when the predicted number of users is close to zero as when it is in the hundreds.

To account for the dependence between the residuals and the predicted values, skforecast allows to partition the residuals into K bins, where each bin is associated with a range of predicted values. Using this strategy, the bootstrapping process samples the residuals from different bins depending on the predicted value, which can improve the coverage of the interval while adjusting the width if necessary, allowing the model to better distribute the uncertainty of its predictions.

Internally, skforecast uses a QuantileBinner class to bin data into quantile-based bins using numpy.percentile. This class is similar to KBinsDiscretizer but faster for binning data into quantile-based bins. Bin intervals are defined following the convention: bins[i-1] <= x < bins[i]. The binning process can be adjusted using the argument binner_kwargs of the Forecaster object.

# Create and train forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
                 regressor     = LGBMRegressor(**params),
                 lags          = lags,
                 binner_kwargs = {'n_bins': 5}   
             )

forecaster.fit(
    y    = data.loc[:end_validation, 'users'],
    exog = data.loc[:end_validation, exog_features],
    store_in_sample_residuals = True
)

During the training process, the forecaster uses the in-sample predictions to define the intervals at which the residuals are stored depending on the predicted value to which they are related (binner_intervals_ attribute). For example, if the bin "0" has an interval of (5.5, 10.7), it means that it will store the residuals of the predictions that fall within that interval.

When the prediction intervals are calculated, the residuals are sampled from the bin corresponding to the predicted value. This way, the model can adjust the width of the intervals depending on the predicted value, which can help to better distribute the uncertainty of the predictions.

# Intervals associated with the bins
# ==============================================================================
pprint(forecaster.binner_intervals_)

{0: (-0.8943794883271247, 30.676160623625577),
 1: (30.676160623625577, 120.49652689276296),
 2: (120.49652689276296, 209.69596300954962),
 3: (209.69596300954962, 338.3331511270013),
 4: (338.3331511270013, 955.802117392104)}

The set_out_sample_residuals() method will bin the residuals according to the intervals learned during fitting. To avoid using too much memory, the number of residuals stored per bin is limited to 10_000 // self.binner.n_bins_.

# Store out-sample residuals in the forecaster
# ==============================================================================
forecaster.set_out_sample_residuals(
    y_true = data.loc[predictions_val.index, 'users'], 
    y_pred = predictions_val['pred']
)

# Number of out-sample residuals by bin
# ==============================================================================
for k, v in forecaster.out_sample_residuals_by_bin_.items():
    print(f"Bin {k}: n={len(v)}")

Bin 0: n=321
Bin 1: n=315
Bin 2: n=310
Bin 3: n=534
Bin 4: n=752

# Distribution of the residual by bin
# ==============================================================================
out_sample_residuals_by_bin_df = pd.DataFrame(
    dict(
        [(k, pd.Series(v))
         for k, v in forecaster.out_sample_residuals_by_bin_.items()]
    )
)
fig, ax = plt.subplots(figsize=(6, 3))
out_sample_residuals_by_bin_df.boxplot(ax=ax)
ax.set_title("Distribution of residuals by bin", fontsize=12)
ax.set_xlabel("Bin", fontsize=10)
ax.set_ylabel("Residuals", fontsize=10)
plt.show();

The box plots show how the spread and magnitude of the residuals differ depending on the predicted value. The residuals are higher and more dispersed when the predicted value is higher (higer bin), which is consistent with the intuition that errors tend to be larger when the predicted value is larger.

# Summary information of bins
# ======================================================================================
bins_summary = {
    key: pd.DataFrame(value).describe().T.assign(bin=key)
    for key, value
    in forecaster.out_sample_residuals_by_bin_.items()
}
bins_summary = pd.concat(bins_summary.values()).set_index("bin")
bins_summary.insert(0, "interval", bins_summary.index.map(forecaster.binner_intervals_))
bins_summary['interval'] = bins_summary['interval'].apply(lambda x: np.round(x, 2))
bins_summary
interval count mean std min 25% 50% 75% max
bin
0 [-0.89, 30.68] 321.0 1.113833 12.168815 -19.168802 -4.060555 -0.435406 3.392902 150.505840
1 [30.68, 120.5] 315.0 1.560517 31.195637 -77.399525 -13.424717 -3.511859 10.819653 356.446585
2 [120.5, 209.7] 310.0 17.209087 51.763411 -147.240066 -7.478638 15.740146 38.113001 300.170968
3 [209.7, 338.33] 534.0 14.883687 69.231176 -241.322880 -18.266984 10.051186 42.654985 464.619346
4 [338.33, 955.8] 752.0 18.740171 105.830048 -485.278643 -23.429556 25.356507 77.634913 382.818946

Finally, the prediction intervals estimated again, this time using out-sample residuals conditioned on the predicted values.

# Backtesting with prediction intervals in test data using out-sample residuals
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_validation]))
metric, predictions = backtesting_forecaster(
                          forecaster              = forecaster,
                          y                       = data['users'],
                          exog                    = data[exog_features],
                          cv                      = cv,
                          metric                  = 'mean_absolute_error',
                          interval                = [10, 90],  # 80% prediction interval
                          interval_method         = 'bootstrapping',
                          n_boot                  = 150,
                          use_in_sample_residuals = False,  # Use out-sample residuals
                          use_binned_residuals    = True,   # Residuals conditioned on predicted values
                      )
predictions.head(3)

  0%|          | 0/19 [00:00<?, ?it/s]
pred lower_bound upper_bound
2012-10-02 00:00:00 60.399647 38.496874 92.876947
2012-10-02 01:00:00 17.617464 9.065502 43.844047
2012-10-02 02:00:00 9.002365 -0.636921 26.285576 
# Plot intervals
# ==============================================================================
plot_predicted_intervals(
    predictions     = predictions,
    y_true          = data_test,
    target_variable = "users",
    xaxis_title     = "Date time",
    yaxis_title     = "users",
)

# Predicted interval coverage (on test data)
# ==============================================================================
coverage = calculate_coverage(
               y_true      = data.loc[end_validation:, 'users'],
               lower_bound = predictions["lower_bound"], 
               upper_bound = predictions["upper_bound"]
           )
print(f"Predicted interval coverage: {round(100 * coverage, 2)} %")

# Area of the interval
# ==============================================================================
area = (predictions["upper_bound"] - predictions["lower_bound"]).sum()
print(f"Area of the interval: {round(area, 2)}")
Oct 32012Oct 5Oct 7Oct 9Oct 11Oct 13Oct 15Oct 17Oct 1902004006008001000
Real valuePredictionDate timeusers
Predicted interval coverage: 86.4 %
Area of the interval: 95072.24

When using out-sample residuals conditioned on the predicted value, the area of the interval is significantly reduced and the uncertainty is mainly allocated to the predictions with high values. However, the empirical coverage is still above the expected coverage, which means that the estimated intervals are conservative.

The follwing plot compares the prediction intervals obtained using in-sample residuals, out-sample residuals, and out-sample residuals conditioned on the predicted values.

# Plot intervals using: in-sample residuals, out-sample residuals and binned residuals
# ==============================================================================
predictions_out_sample_residuals_binned = predictions.copy()
fig, ax = plt.subplots(figsize=(8, 4))
ax.fill_between(
    data_test.index,
    predictions_out_sample_residuals["lower_bound"],
    predictions_out_sample_residuals["upper_bound"],
    color='gray',
    alpha=0.9,
    label='Out-sample residuals',
    zorder=1
)
ax.fill_between(
    data_test.index,
    predictions_out_sample_residuals_binned["lower_bound"],
    predictions_out_sample_residuals_binned["upper_bound"],
    color='#fc4f30',
    alpha=0.7,
    label='Out-sample binned residuals',
    zorder=2
)

ax.fill_between(
    data_test.index,
    predictions_in_sample_residuals["lower_bound"],
    predictions_in_sample_residuals["upper_bound"],
    color='#30a2da',
    alpha=0.9,
    label='In-sample residuals',
    zorder=3
)
ax.set_xlim(pd.to_datetime(["2012-10-08 00:00:00", "2012-10-15 00:00:00"]))
ax.set_title("Prediction intervals with different residuals", fontsize=12)
ax.legend();

⚠ Warning

Probabilistic forecasting in production The correct estimation of prediction intervals depends on the residuals being representative of future errors. For this reason, out-of-sample residuals should be used. However, the dynamics of the series and models can change over time, so it is important to monitor and regularly update the residuals. It can be done easily using the set_out_sample_residuals() method.

Prediction of multiple intervals

The backtesting_forecaster function not only allows to estimate a single prediction interval, but also to estimate multiple quantiles (percentiles) from which multiple prediction intervals can be constructed. This is useful to evaluate the quality of the prediction intervals for a range of probabilities. Furthermore, it has almost no additional computational cost compared to estimating a single interval.

Next, several percentiles are predicted and from these, prediction intervals are created for different nominal coverage levels - 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90% and 95% - and their actual coverage is assessed.

# Prediction intervals for different nominal coverages
# ==============================================================================
quantiles = [2.5, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 97.5]
intervals = [[2.5, 97.5], [5, 95], [10, 90], [15, 85], [20, 80], [30, 70], [35, 65], [40, 60], [45, 55]]
observed_coverages = []
observed_areas = []

metric, predictions = backtesting_forecaster(
                          forecaster              = forecaster,
                          y                       = data['users'],
                          exog                    = data[exog_features],
                          cv                      = cv,
                          metric                  = 'mean_absolute_error',
                          interval                = quantiles,
                          interval_method         = 'bootstrapping',
                          n_boot                  = 150,
                          use_in_sample_residuals = False,  # Use out-sample residuals
                          use_binned_residuals    = True
                      )
predictions.head()

  0%|          | 0/19 [00:00<?, ?it/s]
pred p_2.5 p_5 p_10 p_15 p_20 p_25 p_30 p_35 p_40 ... p_55 p_60 p_65 p_70 p_75 p_80 p_85 p_90 p_95 p_97.5
2012-10-02 00:00:00 60.399647 26.540465 32.237144 38.496874 42.515102 46.248204 48.730080 49.747541 50.830767 53.532796 ... 59.877370 61.388407 63.572870 66.179578 70.417796 77.232456 82.866190 92.876947 109.483516 118.113906
2012-10-02 01:00:00 17.617464 4.028027 6.993912 9.065502 10.218569 11.732744 13.290492 15.065701 15.542016 16.594937 ... 19.700862 21.330240 22.453599 25.298972 28.853490 32.110319 35.993433 43.844047 68.261638 77.072027
2012-10-02 02:00:00 9.002365 -5.454406 -2.921308 -0.636921 2.627889 4.072849 5.556213 6.372106 7.170950 8.269832 ... 11.673119 12.670580 14.060076 15.750417 17.660921 19.929581 23.416450 26.285576 41.378533 52.759679
2012-10-02 03:00:00 5.306644 -7.830956 -6.205384 -1.102749 -0.500265 1.101968 2.283863 3.161327 4.006352 4.764298 ... 6.650199 7.561984 8.280507 9.689953 10.880484 11.786155 14.400937 17.854639 24.489084 41.218966
2012-10-02 04:00:00 9.439573 -6.712543 -2.292124 3.206393 5.276201 5.718478 6.576003 7.203672 8.176026 9.025843 ... 11.509308 12.074734 12.427330 13.552448 14.515979 15.536160 17.744162 22.566557 27.379155 53.829421

5 rows × 22 columns

# Calculate coverage and area for each interval
# ==============================================================================
for interval in intervals:
    observed_coverage = calculate_coverage(
                            y_true      = data.loc[end_validation:, 'users'],
                            lower_bound = predictions[f"p_{interval[0]}"], 
                            upper_bound = predictions[f"p_{interval[1]}"]
                        )
    observed_area = (predictions[f"p_{interval[1]}"] - predictions[f"p_{interval[0]}"]).sum()
    observed_coverages.append(100 * observed_coverage)
    observed_areas.append(observed_area)

results = pd.DataFrame({
              'Interval': intervals,
              'Nominal coverage': [interval[1] - interval[0] for interval in intervals],
              'Observed coverage': observed_coverages,
              'Area': observed_areas
          })
results.round(1)
Interval Nominal coverage Observed coverage Area
0 [2.5, 97.5] 95.0 96.7 163585.0
1 [5, 95] 90.0 93.4 129723.9
2 [10, 90] 80.0 86.4 95072.2
3 [15, 85] 70.0 79.8 73890.3
4 [20, 80] 60.0 74.1 58018.5
5 [30, 70] 40.0 51.1 34447.4
6 [35, 65] 30.0 40.6 24832.8
7 [40, 60] 20.0 26.5 16087.9
8 [45, 55] 10.0 12.5 8026.3

Predict boostrap, interval, quantile and distribution

The previous sections have demonstrated the use of the backtesting process to estimate the prediction interval over a given period of time. The goal is to mimic the behavior of the model in production by running predictions at regular intervals, incrementally updating the input data.

Alternatively, it is possible to run a single prediction that forecasts N steps ahead without going through the entire backtesting process. In such cases, skforecast provides four different methods: predict_bootstrapping, predict_interval, predict_quantile and predict_distribution. For detailed information on how to use these methods, please refer to the documentation.

Conformal Prediction

Conformal prediction is a framework for constructing prediction intervals that are guaranteed to contain the true value with a specified probability (coverage probability). It works by combining the predictions of a point-forecasting model with its past residuals—differences between previous predictions and actual values. These residuals help estimate the uncertainty in the forecast and determine the width of the prediction interval that is then added to the point forecast. Skforecast implements Split Conformal Prediction (SCP).


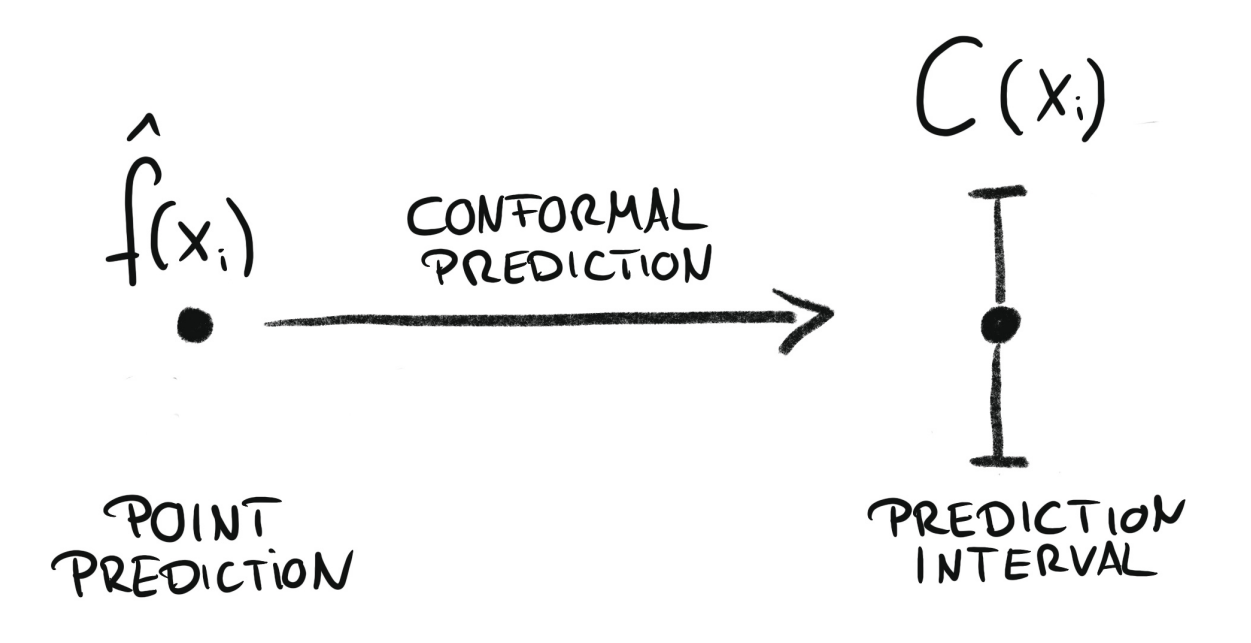
Conformal regression turns point predictions into prediction intervals. Source: Introduction To Conformal Prediction With Python: A Short Guide For Quantifying Uncertainty Of Machine Learning Models by Christoph Molnar https://leanpub.com/conformal-prediction

Conformal methods can also calibrate prediction intervals generated by other techniques, such as quantile regression or bootstrapped residuals. In this case, the conformal method adjusts the prediction intervals to ensure that they remain valid with respect to the coverage probability. Skforecast provides this functionality through the ConformalIntervalCalibrator transformer.

⚠ Warning

There are several well-established methods for conformal prediction, each with its own characteristics and assumptions. However, when applied to time series forecasting, their coverage guarantees are only valid for one-step-ahead predictions. For multi-step-ahead predictions, the coverage probability is not guaranteed. Skforecast implements Split Conformal Prediction (SCP) due to its balance between complexity and performance.

A backtesting process is applied to estimate the prediction intervals for the test set, this time using the conformal method. Since the outsample residuals are already stored in the forecaster object, the use_in_sample_residuals argument is set to False, and use_binned_residuals is set to True to allow adaptive intervals.

# Backtesting with prediction intervals in test data using out-sample residuals
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_validation]))
metric, predictions = backtesting_forecaster(
                          forecaster              = forecaster,
                          y                       = data['users'],
                          exog                    = data[exog_features],
                          cv                      = cv,
                          metric                  = 'mean_absolute_error',
                          interval                = 0.8,  # 80% prediction interval
                          interval_method         = 'conformal',
                          use_in_sample_residuals = False,  # Use out-sample residuals
                          use_binned_residuals    = True,   # Adaptive conformal
                      )
predictions.head(3)

  0%|          | 0/19 [00:00<?, ?it/s]
pred lower_bound upper_bound
2012-10-02 00:00:00 60.399647 32.785300 88.013993
2012-10-02 01:00:00 17.617464 8.692943 26.541985
2012-10-02 02:00:00 9.002365 0.077843 17.926886 
# Plot intervals
# ==============================================================================
plot_predicted_intervals(
    predictions     = predictions,
    y_true          = data_test,
    target_variable = "users",
    xaxis_title     = "Date time",
    yaxis_title     = "users",
)

# Predicted interval coverage (on test data)
# ==============================================================================
coverage = calculate_coverage(
               y_true      = data.loc[end_validation:, 'users'],
               lower_bound = predictions["lower_bound"], 
               upper_bound = predictions["upper_bound"]
           )
print(f"Predicted interval coverage: {round(100 * coverage, 2)} %")

# Area of the interval
# ==============================================================================
area = (predictions["upper_bound"] - predictions["lower_bound"]).sum()
print(f"Area of the interval: {round(area, 2)}")
Oct 32012Oct 5Oct 7Oct 9Oct 11Oct 13Oct 15Oct 17Oct 1902004006008001000
Real valuePredictionDate timeusers
Predicted interval coverage: 78.29 %
Area of the interval: 64139.13

The resulting intervals show a slightly lower coverage than the expected 80%, but close to it.

Quantile Regression

Quantile regression is a technique for estimating the conditional quantiles of a response variable. By combining the predictions of two quantile regressors, an interval can be constructed, where each model estimates one of the interval’s boundaries. For example, models trained for Q=0.1 and Q=0.9 produce an 80% prediction interval (90%−10%=80%).

If a machine learning algorithm capable of modeling quantiles is used as the regressor in a forecaster, the predict method will return predictions for a specified quantile. By creating two forecasters, each configured with a different quantile, their predictions can be combined to generate a prediction interval.

As opposed to linear regression, which is intended to estimate the conditional mean of the response variable given certain values of the predictor variables, quantile regression aims at estimating the conditional quantiles of the response variable. For a continuous distribution function, the α-quantile Qα(x) is defined such that the probability of Y being smaller than Qα(x) is, for a given X=x, equal to α. For example, 36% of the population values are lower than the quantile Q=0.36. The most known quantile is the 50%-quantile, more commonly called the median.

By combining the predictions of two quantile regressors, it is possible to build an interval. Each model estimates one of the limits of the interval. For example, the models obtained for Q=0.1 and Q=0.9 produce an 80% prediction interval (90% - 10% = 80%).

Several machine learning algorithms are capable of modeling quantiles. Some of them are:

Just as the squared-error loss function is used to train models that predict the mean value, a specific loss function is needed in order to train models that predict quantiles. The most common metric used for quantile regression is calles quantile loss or pinball loss:

pinball(y,ˆy)=1nsamplesnsamples−1∑i=0αmax(yi−ˆyi,0)+(1−α)max(ˆyi−yi,0)

where α is the target quantile, y the real value and ˆy the quantile prediction.

It can be seen that loss differs depending on the evaluated quantile. The higher the quantile, the more the loss function penalizes underestimates, and the less it penalizes overestimates. As with MSE and MAE, the goal is to minimize its values (the lower loss, the better).

Two disadvantages of quantile regression, compared to the bootstrap approach to prediction intervals, are that each quantile needs its regressor and quantile regression is not available for all types of regression models. However, once the models are trained, the inference is much faster since no iterative process is needed.

This type of prediction intervals can be easily estimated using ForecasterDirect and ForecasterDirectMultiVariate models.

⚠ Warning

Forecasters of type ForecasterDirect are slower than ForecasterRecursive because they require training one model per step. Although they can achieve better performance, their scalability is an important limitation when many steps need to be predicted. 
# Create forecasters: one for each limit of the interval
# ==============================================================================
# The forecasters obtained for alpha=0.1 and alpha=0.9 produce a 80% confidence
# interval (90% - 10% = 80%).

# Forecaster for quantile 10%
forecaster_q10 = ForecasterDirect(
                     regressor = LGBMRegressor(
                                     objective    = 'quantile',
                                     metric       = 'quantile',
                                     alpha        = 0.1,
                                     random_state = 15926,
                                     verbose      = -1
                                     
                                 ),
                     lags  = lags,
                     steps = 24
                 )
# Forecaster for quantile 90%
forecaster_q90 = ForecasterDirect(
                     regressor = LGBMRegressor(
                                     objective    = 'quantile',
                                     metric       = 'quantile',
                                     alpha        = 0.9,
                                     random_state = 15926,
                                     verbose      = -1
                                     
                                 ),
                     lags  = lags,
                     steps = 24
                 )

Next, a bayesian search is performed to find the best hyperparameters for the quantile regressors. When validating a quantile regression model, it is important to use a metric that is coherent with the quantile being evaluated. In this case, the pinball loss is used. Skforecast provides the function create_mean_pinball_loss calculate the pinball loss for a given quantile.

# Bayesian search of hyper-parameters and lags for each quantile forecaster
# ==============================================================================
def search_space(trial):
    search_space  = {
        'n_estimators'  : trial.suggest_int('n_estimators', 100, 500, step=50),
        'max_depth'     : trial.suggest_int('max_depth', 3, 10, step=1),
        'learning_rate' : trial.suggest_float('learning_rate', 0.01, 0.1)
    }

    return search_space

cv = TimeSeriesFold(steps = 24, initial_train_size = len(data[:end_train]))

results_grid_q10 = bayesian_search_forecaster(
                       forecaster   = forecaster_q10,
                       y            = data.loc[:end_validation, 'users'],
                       cv           = cv,
                       metric       = create_mean_pinball_loss(alpha=0.1),
                       search_space = search_space,
                       n_trials     = 10
                   )

results_grid_q90 = bayesian_search_forecaster(
                       forecaster   = forecaster_q90,
                       y            = data.loc[:end_validation, 'users'],
                       cv           = cv,
                       metric       = create_mean_pinball_loss(alpha=0.9),
                       search_space = search_space,
                       n_trials     = 10
                   )

  0%|          | 0/10 [00:00<?, ?it/s]
`Forecaster` refitted using the best-found lags and parameters, and the whole data set: 
  Lags: [  1   2   3  23  24  25 167 168 169] 
  Parameters: {'n_estimators': 450, 'max_depth': 8, 'learning_rate': 0.06499211596098246}
  Backtesting metric: 21.106815983551137

  0%|          | 0/10 [00:00<?, ?it/s]
`Forecaster` refitted using the best-found lags and parameters, and the whole data set: 
  Lags: [  1   2   3  23  24  25 167 168 169] 
  Parameters: {'n_estimators': 400, 'max_depth': 5, 'learning_rate': 0.042560979006008276}
  Backtesting metric: 38.44122580678526

Once the best hyper-parameters have been found for each forecaster, a backtesting process is applied again using the test data.

# Backtesting on test data
# ==============================================================================
cv = TimeSeriesFold(steps = 24, initial_train_size = len(data.loc[:end_validation]))
metric_q10, predictions_q10 = backtesting_forecaster(
                                  forecaster = forecaster_q10,
                                  y          = data['users'],
                                  cv         = cv,
                                  metric     = create_mean_pinball_loss(alpha=0.1)
                              )

metric_q90, predictions_q90 = backtesting_forecaster(
                                  forecaster = forecaster_q90,
                                  y          = data['users'],
                                  cv         = cv,
                                  metric     = create_mean_pinball_loss(alpha=0.9)
                              )
predictions = pd.concat([predictions_q10, predictions_q90], axis=1)
predictions.columns = ['lower_bound', 'upper_bound']
predictions.head(3)

  0%|          | 0/19 [00:00<?, ?it/s]
  0%|          | 0/19 [00:00<?, ?it/s]
lower_bound upper_bound
2012-10-02 00:00:00 39.108177 73.136230
2012-10-02 01:00:00 11.837010 32.588538
2012-10-02 02:00:00 4.453201 14.346566 
# Plot
# ==============================================================================
fig = go.Figure([
    go.Scatter(name='Real value', x=data_test.index, y=data_test['users'], mode='lines'),
    go.Scatter(
        name='Upper Bound', x=predictions.index, y=predictions['upper_bound'],
        mode='lines', marker=dict(color="#444"), line=dict(width=0), showlegend=False
    ),
    go.Scatter(
        name='Lower Bound', x=predictions.index, y=predictions['lower_bound'],
        marker=dict(color="#444"), line=dict(width=0), mode='lines',
        fillcolor='rgba(68, 68, 68, 0.3)', fill='tonexty', showlegend=False
    )
])
fig.update_layout(
    title="Real value vs predicted in test data",
    xaxis_title="Date time",
    yaxis_title="users",
    width=800,
    height=400,
    margin=dict(l=20, r=20, t=35, b=20),
    hovermode="x",
    legend=dict(orientation="h", yanchor="top", y=1.1, xanchor="left", x=0.001)
)
fig.show()
Oct 32012Oct 5Oct 7Oct 9Oct 11Oct 13Oct 15Oct 17Oct 1902004006008001000
Real valueReal value vs predicted in test dataDate timeusers
# Predicted interval coverage (on test data)
# ==============================================================================
coverage = calculate_coverage(
               y_true      = data.loc[end_validation:, 'users'],
               lower_bound = predictions["lower_bound"], 
               upper_bound = predictions["upper_bound"]
           )
print(f"Predicted interval coverage: {round(100 * coverage, 2)} %")

# Area of the interval
# ==============================================================================
area = (predictions["upper_bound"] - predictions["lower_bound"]).sum()
print(f"Area of the interval: {round(area, 2)}")

Predicted interval coverage: 62.28 %
Area of the interval: 109062.92

In this case, the quantile forecasting strategy does not achieve empirical coverage close to the expected coverage (80 percent).

External calibration of prediction intervals

It is frequent that the prediction intervals obtained with the different methods do not achieve the desired coverage because they are under or overconfident. To address this issue, skforecast provides the ConformalIntervalCalibrator transformer, which can be used to calibrate the prediction intervals obtained with other methods.

Session information

import session_info
session_info.show(html=False)

-----
feature_engine      1.8.3
lightgbm            4.6.0
matplotlib          3.10.1
numpy               2.2.5
pandas              2.2.3
plotly              6.0.1
session_info        v1.0.1
skforecast          0.16.0
sklearn             1.6.1
-----
IPython             9.1.0
jupyter_client      8.6.3
jupyter_core        5.7.2
notebook            6.5.7
-----
Python 3.12.9 | packaged by Anaconda, Inc. | (main, Feb  6 2025, 18:56:27) [GCC 11.2.0]
Linux-6.11.0-25-generic-x86_64-with-glibc2.39
-----
Session information updated at 2025-05-13 21:04

Citation

How to cite this document

If you use this document or any part of it, please acknowledge the source, thank you!

Probabilistic forecasting with machine learning by Joaquín Amat Rodrigo and Javier Escobar Ortiz, available under Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0 DEED) at https://cienciadedatos.net/documentos/py42-probabilistic-forecasting.html

How to cite skforecast

If you use skforecast for a publication, we would appreciate if you cite the published software.

Zenodo:

Amat Rodrigo, Joaquin, & Escobar Ortiz, Javier. (2024). skforecast (v0.16.0). Zenodo. https://doi.org/10.5281/zenodo.8382788

APA:

Amat Rodrigo, J., & Escobar Ortiz, J. (2024). skforecast (Version 0.16.0) [Computer software]. https://doi.org/10.5281/zenodo.8382788

BibTeX:

@software{skforecast, author = {Amat Rodrigo, Joaquin and Escobar Ortiz, Javier}, title = {skforecast}, version = {0.16.0}, month = {05}, year = {2025}, license = {BSD-3-Clause}, url = {https://skforecast.org/}, doi = {10.5281/zenodo.8382788} }


Did you like the article? Your support is important

Your contribution will help me to continue generating free educational content. Many thanks! 😊

Become a GitHub Sponsor Become a GitHub Sponsor

Creative Commons Licence

This work by Joaquín Amat Rodrigo and Javier Escobar Ortiz is licensed under a Attribution-NonCommercial-ShareAlike 4.0 International.

Allowed:

  • Share: copy and redistribute the material in any medium or format.

  • Adapt: remix, transform, and build upon the material.

Under the following terms:

  • Attribution: You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.

  • NonCommercial: You may not use the material for commercial purposes.

  • ShareAlike: If you remix, transform, or build upon the material, you must distribute your contributions under the same license as the original.