Si te gusta Skforecast , ayúdanos dándonos una estrella en GitHub! ⭐️
Predicción (forecasting) de la demanda energética con machine learning
Más sobre forecasting en: cienciadedatos.net
- Forecasting series temporales con machine learning
- Modelos ARIMA y SARIMAX
- Forecasting series temporales con gradient boosting: XGBoost, LightGBM y CatBoost
- Global Forecasting: Multi-series forecasting
- Forecasting de la demanda eléctrica con machine learning
- Forecasting con deep learning
- Forecasting de visitas a página web con machine learning
- Forecasting del precio de Bitcoin
- Forecasting probabilístico
- Forecasting de demanda intermitente
- Reducir el impacto del Covid en modelos de forecasting
- Modelar series temporales con tendencia utilizando modelos de árboles
Introducción¶
La predicción de la demanda energética desempeña un papel fundamental en la gestión y planificación de los recursos necesarios para la generación, distribución y utilización de la energía. Predecir la demanda de energía es una tarea compleja en la que influyen factores como los patrones meteorológicos, las condiciones económicas y el comportamiento de la sociedad. Este documento muestra cómo utilizar modelos de machine learning para predecir la demanda de energía.
Series temporales y forecasting
Una serie temporal (time series) es una sucesión de datos ordenados cronológicamente, espaciados a intervalos iguales o desiguales. El proceso de forecasting consiste en predecir el valor futuro de una serie temporal, bien modelando la serie únicamente en función de su comportamiento pasado (autorregresivo) o empleando otras variables externas.
Cuando se trabaja con series temporales, raramente se quiere predecir solo el siguiente elemento de la serie ($t_{+1}$), sino todo un horizonte futuro ($t_{+1}$), ..., ($t_{+n}$)) o un punto alejado en el tiempo ($t_{+n}$). Existen varias estrategias que permiten generar este tipo de predicciones, la librería skforecast recoge las siguientes para series temporales univariantes:
- Forecasting multi-step recursivo: este método consiste en utilizar propias predicciones del modelo como valores de entrada para predecir el siguiente valor. Por ejemplo, para predecir los 5 valores siguientes de una serie temporal, se entrena un modelo para predecir el siguiente valor ($t_{+1}$), y se utiliza este valor para predecir el siguiente ($t_{+2}$), y así sucesivamente. Todo este proceso se automatiza con la clase
ForecasterRecursive.
- Forecasting multi-step directo: este método consiste en entrenar un modelo diferente para cada valor futuro (step) del horizonte de predicción. Por ejemplo, para predecir los 5 siguientes valores de una serie temporal, se entrenan 5 modelos diferentes, uno para cada step. De este modo, las predicciones son independientes entre sí. Todo este proceso se automatiza en la clase
ForecasterDirect.
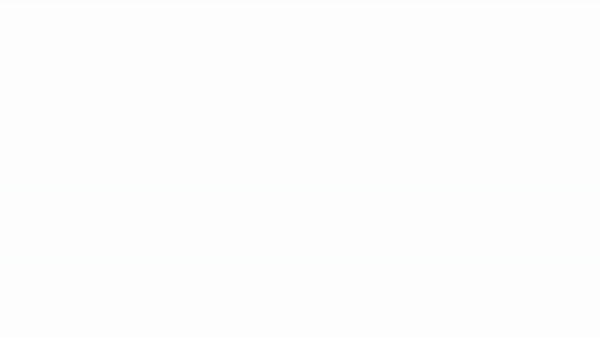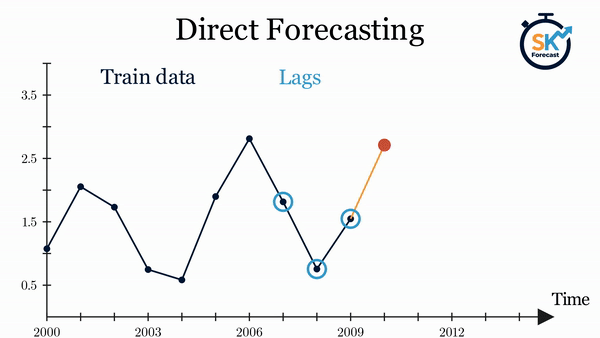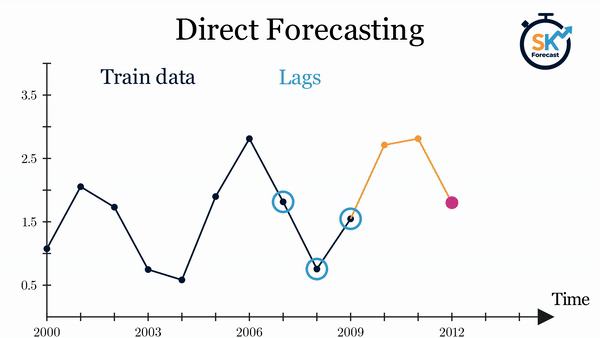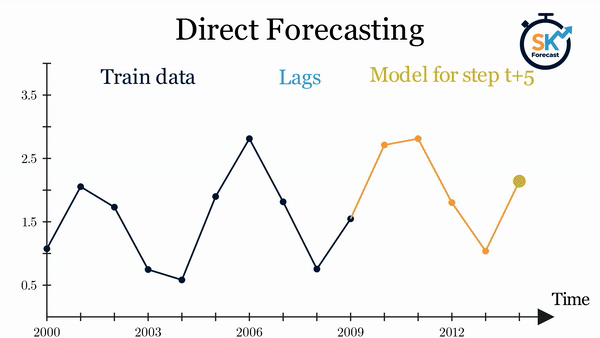
- Forecasting multi-output: Determinados modelos, por ejemplo, las redes neuronales LSTM, son capaces de predecir de forma simultánea varios valores de una secuencia (one-shot). Esta estrategia está disponible con la clase
ForecasterRnn.
✎ Nota
Otros dos ejemplos de cómo utilizar machine learning (*gradient boosting*) para forecasting de series temporales son:Librerías¶
Las librerías utilizadas en este documento son:
# Tratamiento de datos
# ==============================================================================
import numpy as np
import pandas as pd
from astral.sun import sun
from astral import LocationInfo
from skforecast.datasets import fetch_dataset
from feature_engine.datetime import DatetimeFeatures
from feature_engine.creation import CyclicalFeatures
from feature_engine.timeseries.forecasting import WindowFeatures
# Gráficos
# ==============================================================================
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
from skforecast.plot import plot_residuals
import plotly.graph_objects as go
import plotly.io as pio
import plotly.offline as poff
pio.templates.default = "seaborn"
poff.init_notebook_mode(connected=True)
plt.style.use('seaborn-v0_8-darkgrid')
plt.rcParams.update({'font.size': 8})
# Modelado y Forecasting
# ==============================================================================
import skforecast
import lightgbm
import sklearn
from lightgbm import LGBMRegressor
from sklearn.preprocessing import PolynomialFeatures
from sklearn.feature_selection import RFECV
from skforecast.recursive import ForecasterEquivalentDate
from skforecast.recursive import ForecasterRecursive
from skforecast.direct import ForecasterDirect
from skforecast.model_selection import bayesian_search_forecaster
from skforecast.model_selection import backtesting_forecaster
from skforecast.feature_selection import select_features
from skforecast.model_selection import TimeSeriesFold
from skforecast.preprocessing import RollingFeatures
import shap
# Configuración warnings
# ==============================================================================
import warnings
warnings.filterwarnings('once')
color = '\033[1m\033[38;5;208m'
print(f"{color}Versión skforecast: {skforecast.__version__}")
print(f"{color}Versión scikit-learn: {sklearn.__version__}")
print(f"{color}Versión lightgbm: {lightgbm.__version__}")
print(f"{color}Versión pandas: {pd.__version__}")
print(f"{color}Versión numpy: {np.__version__}")
Datos¶
Se dispone de una serie temporal de la demanda de electricidad (MW) para el estado de Victoria (Australia) desde 2011-12-31 hasta 2014-12-31. Los datos empleados en este documento se han obtenido del paquete de R tsibbledata. El set de datos contiene 5 columnas y 52608 registros completos. La información de cada columna es:
- Time: fecha y hora del registro.
- Date: fecha del registro
- Demand: demanda de electricidad (MW).
- Temperature: temperatura en Melbourne, capital de Victoria.
- Holiday: indicador si el día es festivo (vacaciones).
# Descarga de datos
# ==============================================================================
datos = fetch_dataset(name='vic_electricity', raw=True)
datos.info()
La columna Time está almacenada como string. Para convertirla en datetime, se emplea la función pd.to_datetime(). Una vez en formato datetime, y para hacer uso de las funcionalidades de pandas, se establece como índice. Además, dado que los datos se han registrado cada 30 minutos, se indica la frecuencia '30min'.
# Conversión del formato fecha
# ==============================================================================
datos['Time'] = pd.to_datetime(datos['Time'], format='%Y-%m-%dT%H:%M:%SZ')
datos = datos.set_index('Time')
datos = datos.asfreq('30min')
datos = datos.sort_index()
datos.head(2)
Uno de los primeros análisis que hay que realizar al trabajar con series temporales es verificar si la serie está completa.
# Verificar que un índice temporal está completo
# ==============================================================================
fecha_inicio = datos.index.min()
fecha_fin = datos.index.max()
date_range_completo = pd.date_range(start=fecha_inicio, end=fecha_fin, freq=datos.index.freq)
print(f"Índice completo: {(datos.index == date_range_completo).all()}")
print(f"Filas con valores ausentes: {datos.isnull().any(axis=1).mean()}")
# Completar huecos en un índice temporal
# ==============================================================================
# datos.asfreq(freq='30min', fill_value=np.nan)
Aunque los datos se encuentran en intervalos de 30 minutos, el objetivo es crear un modelo capaz de predecir la demanda eléctrica a nivel horario, por lo que se tienen que agregar los datos. Este tipo de transformación es muy sencillas si se combina el índice DatetimeIndex de pandas y su método resample().
Es muy importante utilizar correctamente los argumentos closed='left' y label='right' para no introducir en el entrenamiento información a futuro (leakage)). Supóngase que se dispone de valores para las 10:10, 10:30, 10:45, 11:00, 11:12 y 11:30. Si se quiere obtener el promedio horario, el valor asignado a las 11:00 debe calcularse utilizando los valores de las 10:10, 10:30 y 10:45; y el de las 12:00, con el valor de las 11:00, 11:12 y 11:30.
Para el valor promedio de las 11:00 no se incluye el valor puntual de las 11:00 por que, en la realidad, en ese momento exacto no se dispone todavía del valor.
# Agregado en intervalos de 1H
# ==============================================================================
# Se elimina la columna Date para que no genere error al agregar.
datos = datos.drop(columns='Date')
datos = (
datos
.resample(rule="h", closed="left", label="right")
.agg({
"Demand": "mean",
"Temperature": "mean",
"Holiday": "mean",
})
)
datos
El set de datos empieza el 2011-12-31 14:00:00 y termina el 2014-12-31 13:00:00. Se descartan los primeros 10 y los últimos 13 registros para que empiece el 2012-01-01 00:00:00 y termine el 2014-12-30 23:00:00. Además, para poder optimizar los hiperparámetros del modelo y evaluar su capacidad predictiva, se dividen los datos en 3 conjuntos, uno de entrenamiento, uno de validación y otro de test.
# Separación datos train-val-test
# ==============================================================================
datos = datos.loc['2012-01-01 00:00:00':'2014-12-30 23:00:00', :].copy()
fin_train = '2013-12-31 23:59:00'
fin_validacion = '2014-11-30 23:59:00'
datos_train = datos.loc[: fin_train, :].copy()
datos_val = datos.loc[fin_train:fin_validacion, :].copy()
datos_test = datos.loc[fin_validacion:, :].copy()
print(f"Fechas train : {datos_train.index.min()} --- {datos_train.index.max()} (n={len(datos_train)})")
print(f"Fechas validacion : {datos_val.index.min()} --- {datos_val.index.max()} (n={len(datos_val)})")
print(f"Fechas test : {datos_test.index.min()} --- {datos_test.index.max()} (n={len(datos_test)})")
Exploración gráfica¶
La exploración gráfica de series temporales es una forma eficaz de identificar tendencias, patrones y estacionalidad. Esto, a su vez, ayuda a orientar la selección del modelo de forecasting más adecuado.
Gráfico de la serie temporal¶
Serie temporal completa
# Gráfico interactivo de la serie temporal
# ==============================================================================
fig = go.Figure()
fig.add_trace(go.Scatter(x=datos_train.index, y=datos_train['Demand'], mode='lines', name='Train'))
fig.add_trace(go.Scatter(x=datos_val.index, y=datos_val['Demand'], mode='lines', name='Validation'))
fig.add_trace(go.Scatter(x=datos_test.index, y=datos_test['Demand'], mode='lines', name='Test'))
fig.update_layout(
title = 'Demanda eléctrica horaria',
xaxis_title="Fecha",
yaxis_title="Demanda (MWh)",
legend_title="Partición:",
width=750,
height=370,
margin=dict(l=20, r=20, t=35, b=20),
legend=dict(orientation="h", yanchor="top", y=1, xanchor="left", x=0.001)
)
#fig.update_xaxes(rangeslider_visible=True)
fig.show()
El gráfico anterior muestra que la demanda eléctrica tiene estacionalidad anual. Se observa un incremento centrado en el mes de Julio y picos de demanda muy acentuados entre enero y marzo.
Sección de la serie temporal
Debido a la varianza de la serie temporal, no es posible apreciar con un solo gráfico el posible patrón intradiario.
# Gráfico serie temporal con zoom
# ==============================================================================
zoom = ('2013-05-01 14:00:00','2013-06-01 14:00:00')
fig = plt.figure(figsize=(8, 4))
grid = plt.GridSpec(nrows=8, ncols=1, hspace=0.6, wspace=0)
main_ax = fig.add_subplot(grid[1:3, :])
zoom_ax = fig.add_subplot(grid[5:, :])
datos.Demand.plot(ax=main_ax, c='black', alpha=0.5, linewidth=0.5)
min_y = min(datos.Demand)
max_y = max(datos.Demand)
main_ax.fill_between(zoom, min_y, max_y, facecolor='blue', alpha=0.5, zorder=0)
main_ax.set_xlabel('')
datos.loc[zoom[0]: zoom[1]].Demand.plot(ax=zoom_ax, color='blue', linewidth=1)
main_ax.set_title(f'Demanda electricidad: {datos.index.min()}, {datos.index.max()}', fontsize=10)
zoom_ax.set_title(f'Demanda electricidad: {zoom}', fontsize=10)
zoom_ax.set_xlabel('')
plt.subplots_adjust(hspace=1)
Al aplicar zoom sobre la serie temporal, se hace patente una clara estacionalidad semanal, con consumos más elevados durante la semana laboral (lunes a viernes) y menor en los fines de semana. Se observa también que existe una clara correlación entre el consumo de un día con el del día anterior.
Gráfico de estacionalidad¶
# Estacionalidad anual, semanal y diaria
# ==============================================================================
fig, axs = plt.subplots(2, 2, figsize=(8, 5), sharex=False, sharey=True)
axs = axs.ravel()
# Distribusión de demanda por mes
datos['month'] = datos.index.month
datos.boxplot(column='Demand', by='month', ax=axs[0], flierprops={'markersize': 3, 'alpha': 0.3})
datos.groupby('month')['Demand'].median().plot(style='o-', linewidth=0.8, ax=axs[0])
axs[0].set_ylabel('Demand')
axs[0].set_title('Distribución de demanda por mes', fontsize=9)
# Distribusión de demanda por día de la semana
datos['week_day'] = datos.index.day_of_week + 1
datos.boxplot(column='Demand', by='week_day', ax=axs[1], flierprops={'markersize': 3, 'alpha': 0.3})
datos.groupby('week_day')['Demand'].median().plot(style='o-', linewidth=0.8, ax=axs[1])
axs[1].set_ylabel('Demand')
axs[1].set_title('Distribución de demanda por día de la semana', fontsize=9)
# Distribusión de demanda por hora del día
datos['hour_day'] = datos.index.hour + 1
datos.boxplot(column='Demand', by='hour_day', ax=axs[2], flierprops={'markersize': 3, 'alpha': 0.3})
datos.groupby('hour_day')['Demand'].median().plot(style='o-', linewidth=0.8, ax=axs[2])
axs[2].set_ylabel('Demand')
axs[2].set_title('Distribución de demanda por hora del día', fontsize=9)
# Distribusión de demanda por día de la semana y hora del día
mean_day_hour = datos.groupby(["week_day", "hour_day"])["Demand"].mean()
mean_day_hour.plot(ax=axs[3])
axs[3].set(
title = "Promedio de demanda",
xticks = [i * 24 for i in range(7)],
xticklabels = ["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"],
xlabel = "Día y hora",
ylabel = "Demand"
)
axs[3].title.set_size(10)
fig.suptitle("Gráficos de estacionalidad", fontsize=12)
fig.tight_layout()
Se observa que hay una estacionalidad anual, con valores de demanda (mediana) superiores en los meses de junio, julio y agosto, y con elevados picos de demanda en los meses de noviembre, diciembre, enero, febrero y marzo. Se aprecia una estacionalidad semanal, con valores de demanda inferiores durante el fin de semana. También existe una estacionalidad diaria, ya que la demanda se reduce entre las 16:00 y las 21:00 horas.
Gráficos de autocorrelación¶
Los gráficos de autocorrelación muestran la correlación entre una serie temporal y sus valores pasados. Son una herramienta útil para identificar el orden de un modelo autorregresivo, es decir, los valores pasados (lags) que se deben incluir en el modelo.
La función de autocorrelación (ACF) mide la correlación entre una serie temporal y sus valores pasados. La función de autocorrelación parcial (PACF) mide la correlación entre una serie temporal y sus valores pasados, pero solo después de eliminar las variaciones explicadas por los valores pasados intermedios.
# Gráfico autocorrelación
# ==============================================================================
fig, ax = plt.subplots(figsize=(5, 2))
plot_acf(datos.Demand, ax=ax, lags=60)
plt.show()
# Gráfico autocorrelación parcial
# ==============================================================================
fig, ax = plt.subplots(figsize=(5, 2))
plot_pacf(datos.Demand, ax=ax, lags=60)
plt.show()
Los gráficos de autocorrelación y autocorrelación parcial muestran una clara asociación entre la demanda de una hora y las horas anteriores, así como entre la demanda de una hora y la demanda de esa misma hora los días anteriores. Este tipo de correlación, es un indicativo de que los modelos autorregresivos pueden funcionar bien.
Baseline¶
Al enfrentarse a un problema de forecasting, es recomendable disponer de un modelo de referencia (baseline). Suele tratarse de un modelo muy sencillo que puede utilizarse como referencia para evaluar si merece la pena aplicar modelos más complejos.
Skforecast permite crear fácilmente un modelo de referencia con su clase ForecasterEquivalentDate. Este modelo, también conocido como Seasonal Naive Forecasting, simplemente devuelve el valor observado en el mismo periodo de la temporada anterior (por ejemplo, el mismo día laboral de la semana anterior, la misma hora del día anterior, etc.).
A partir del análisis exploratorio realizado, el modelo de referencia será el que prediga cada hora utilizando el valor de la misma hora del día anterior.
✎ Nota
En las siguientes celdas de código, se entrena un modelo *baseline* y se evalúa su capacidad predictiva mediante un proceso de *backtesting*. Si este concepto es nuevo para ti, no te preocupes, se explicará en detalle a lo largo del documento. Por ahora, basta con saber que el proceso de *backtesting* consiste en entrenar el modelo con una cierta cantidad de datos y evaluar su capacidad predictiva con los datos que el modelo no ha visto. La métrica del error se utilizará como referencia para comparar la capacidad predictiva de los modelos más complejos que se implementarán a lo largo del documento.# Crear un baseline: valor de la misma hora del día anterior
# ==============================================================================
forecaster = ForecasterEquivalentDate(
offset = pd.DateOffset(days=1),
n_offsets = 1
)
# Entremaiento del forecaster
# ==============================================================================
forecaster.fit(y=datos.loc[:fin_validacion, 'Demand'])
forecaster
# Backtesting
# ==============================================================================
cv = TimeSeriesFold(
steps = 24,
initial_train_size = len(datos.loc[:fin_validacion]),
refit = False
)
metrica, predicciones = backtesting_forecaster(
forecaster = forecaster,
y = datos['Demand'],
cv = cv,
metric = 'mean_absolute_error',
n_jobs = 'auto',
verbose = False,
show_progress = True
)
metrica
El error del modelo base se utiliza como referencia para evaluar si merece la pena aplicar los modelos más complejos.
Modelo autoregresivo recursivo¶
Se entrena un modelo autorregresivo recursivo (ForecasterRecursive) con un gradient boosting LGBMRegressor como regresor para predecir la demanda de energía de las próximas 24 horas.
Se utilizan como predictores los valores de consumo de las últimas 24 horas (24 lags) así como la media movil de los últimos 3 días. Los hiperparámetros del regresor se dejan en sus valores por defecto.
# Crear el forecaster
# ==============================================================================
window_features = RollingFeatures(stats=["mean"], window_sizes=24 * 3)
forecaster = ForecasterRecursive(
regressor = LGBMRegressor(random_state=15926, verbose=-1),
lags = 24,
window_features = window_features
)
# Entrena el forecaster
# ==============================================================================
forecaster.fit(y=datos.loc[:fin_validacion, 'Demand'])
forecaster
Backtesting¶
Para obtener una estimación robusta de la capacidad predictiva del modelo, se realiza un proceso de backtesting. El proceso de backtesting consiste en generar una predicción para cada observación del conjunto de test, siguiendo el mismo procedimiento que se seguiría si el modelo estuviese en producción, y finalmente comparar el valor predicho con el valor real.
El proceso de backtesting se aplica mediante la función backtesting_forecaster(). Para este caso de uso, la simulación se lleva a cabo de la siguiente manera: el modelo se entrena con datos de 2012-01-01 00:00 a 2014-11-30 23:59, y luego predice las siguientes 24 horas cada día a las 23:59. La métrica de error utilizada es el error absoluto medio (MAE).
# Backtesting
# ==============================================================================
metrica, predicciones = backtesting_forecaster(
forecaster = forecaster,
y = datos['Demand'],
cv = cv,
metric = 'mean_absolute_error',
n_jobs = 'auto',
verbose = True, # False para no mostrar info
show_progress = True
)
# Gráfico prediccion vs valores reales
# ==============================================================================
fig = go.Figure()
trace1 = go.Scatter(x=datos_test.index, y=datos_test['Demand'], name="test", mode="lines")
trace2 = go.Scatter(x=predicciones.index, y=predicciones['pred'], name="prediction", mode="lines")
fig.add_trace(trace1)
fig.add_trace(trace2)
fig.update_layout(
title="Predicción vs valores reales en test",
xaxis_title="Date time",
yaxis_title="Demand",
width=750,
height=370,
margin=dict(l=20, r=20, t=35, b=20),
legend=dict(orientation="h", yanchor="top", y=1.01, xanchor="left", x=0)
)
fig.show()
# Error backtest
# ==============================================================================
metrica
El modelo autorregresivo alcanza un MAE inferior al del modelo baseline. Esto significa que el modelo autorregresivo es capaz de predecir la demanda de electricidad del día siguiente con mayor precisión que el modelo utilizado como referencia.
Optimización de hiperparámetros (tuning)¶
El ForecasterRecursive entrenado utiliza los primeros 24 lags y un modelo LGMBRegressor con los hiperparámetros por defecto. Sin embargo, no hay ninguna razón por la que estos valores sean los más adecuados. Para encontrar los mejores hiperparámetros, se realiza una Búsqueda Bayesiana utilizando la función bayesian_search_forecaster(). La búsqueda se lleva a cabo utilizando el mismo proceso de backtesting que antes, pero cada vez, el modelo se entrena con diferentes combinaciones de hiperparámetros y lags. Es importante señalar que la búsqueda de hiperparámetros debe realizarse utilizando el conjunto de validación, nunca con los datos de test.
💡 Tip
El proceso de búsqueda de hiperparámetros puede requerir una cantidad notable de tiempo, sobre todo si se utiliza una estrategia de validación basada en backtesting (TimeSeriesFold). Una alternativa más rápida consiste en utilizar una estrategia de validación basada en predicciones *one-step-ahead* (OneStepAheadFold). Esta estrategia es más rápida pero puede no ser tan precisa como la validación basada en backtesting. Para obtener una descripción más detallada de los pros y los contras de cada estrategia, consulte la sección [backtesting vs one-step-ahead](https://skforecast.org/latest/faq/parameters-search-backetesting-vs-one-step-ahead.html).
# Búsqueda bayesiana de hiperparámetros
# ==============================================================================
forecaster = ForecasterRecursive(
regressor = LGBMRegressor(random_state=15926, verbose=-1),
lags = 24, # Este valor se modifica durante la búsqueda
window_features = window_features
)
# Lags utilizados como predictores
lags_grid = [24, [1, 2, 3, 23, 24, 25, 47, 48, 49]]
# Espacio de búsqueda de hiperparámetros
def search_space(trial):
search_space = {
'n_estimators' : trial.suggest_int('n_estimators', 600, 2000, step=100),
'max_depth' : trial.suggest_int('max_depth', 3, 10, step=1),
'learning_rate': trial.suggest_float('learning_rate', 0.01, 0.5),
'reg_alpha' : trial.suggest_float('reg_alpha', 0, 1, step=0.1),
'reg_lambda' : trial.suggest_float('reg_lambda', 0, 1, step=0.1),
'lags' : trial.suggest_categorical('lags', lags_grid)
}
return search_space
# Partición de entrenamiento y validación
cv_search = TimeSeriesFold(
steps = 24,
initial_train_size = len(datos[:fin_train]),
refit = False,
)
resultados_busqueda, frozen_trial = bayesian_search_forecaster(
forecaster = forecaster,
y = datos.loc[:fin_validacion, 'Demand'],
cv = cv_search,
metric = 'mean_absolute_error',
search_space = search_space,
n_trials = 10, # Aumentar para una búsqueda más exhaustiva
random_state = 123,
return_best = True,
n_jobs = 'auto',
verbose = False,
show_progress = True
)
# Resultados de la búsqueda
# ==============================================================================
best_params = resultados_busqueda.at[0, 'params']
best_params = best_params | {'random_state': 15926, 'verbose': -1}
best_lags = resultados_busqueda.at[0, 'lags']
resultados_busqueda.head(3)
Al indicar return_best = True, el objeto forecaster se actualiza automáticamente con la mejor configuración encontrada y se entrena con el conjunto de datos completo. Este modelo final puede utilizarse para obtener predicciones sobre nuevos datos.
# Mejor modelo
# ==============================================================================
forecaster
Backtesting con datos de test¶
Una vez identificada la mejor combinación de hiperparámetros utilizando los datos de validación, se evalúa la capacidad predictiva del modelo cuando se aplica al conjunto de test. Se recomienda revisar la documentación de la función backtesting_forecaster() para comprender mejor sus capacidades. Esto ayudará a utilizar todo su potencial para analizar la capacidad predictiva del modelo.
# Backtest modelo final
# ==============================================================================)
metrica, predicciones = backtesting_forecaster(
forecaster = forecaster,
y = datos['Demand'],
cv = cv,
metric = 'mean_absolute_error',
n_jobs = 'auto',
verbose = False,
show_progress = True
)
display(metrica)
predicciones.head()
Tras la optimización de lags e hiperparámetros, se ha conseguido reducir el error de predicción de forma notable.
Variables exógenas¶
Hasta ahora, sólo se han utilizado como predictores los valores pasados (lags) de la serie temporal. Sin embargo, es posible incluir otras variables como predictores. Estas variables se conocen como variables exógenas (features) y su uso puede mejorar la capacidad predictiva del modelo. Un punto muy importante que hay que tener en cuenta es que los valores de las variables exógenas deben conocerse en el momento de la predicción.
Ejemplos habituales de variables exógenas son aquellas obtenidas del calendario, como el día de la semana, el mes, el año o los días festivos. Las variables meteorológicas como la temperatura, la humedad y el viento también entran en esta categoría, al igual que las variables económicas como la inflación y los tipos de interés.
⚠ Warning
Las variables exógenas deben conocerse en el momento de la predicción. Por ejemplo, si se utiliza la temperatura como variable exógena, el valor de la temperatura para la hora siguiente debe conocerse en el momento de la previsión. Si no se conoce el valor de la temperatura, la predicción no será posible.Las variables meteorológicas deben utilizarse con precaución. Cuando el modelo se pone en producción, las condiciones meteorológicas futuras no se conocen, sino que son predicciones realizadas por los servicios meteorológicos. Al tratarse de predicciones, introducen errores en el modelo de previsión. Como consecuencia, es probable que las predicciones del modelo empeoren. Una forma de anticiparse a este problema, y conocer (no evitar) el rendimiento esperado del modelo, es utilizar las previsiones meteorológicas disponibles en el momento en que se entrena el modelo, en lugar de las condiciones reales registradas.
A continuación, se crean variables exógenas basadas en información del calendario, las horas de salida y puesta del sol, la temperatura y los días festivos. Estas nuevas variables se añaden a los conjuntos de entrenamiento, validación y test, y se utilizan como predictores en el modelo autorregresivo.
# Variables basadas en el calendario
# ==============================================================================
features_to_extract = [
'month',
'week',
'day_of_week',
'hour'
]
calendar_transformer = DatetimeFeatures(
variables='index',
features_to_extract=features_to_extract,
drop_original=True,
)
variables_calendario = calendar_transformer.fit_transform(datos)[features_to_extract]
# Variables basadas en la luz solar
# ==============================================================================
location = LocationInfo(
latitude=-37.8,
longitude=144.95,
timezone='Australia/Melbourne'
)
sunrise_hour = [
sun(location.observer, date=date, tzinfo=location.timezone)['sunrise']
for date in datos.index
]
sunset_hour = [
sun(location.observer, date=date, tzinfo=location.timezone)['sunset']
for date in datos.index
]
sunrise_hour = pd.Series(sunrise_hour, index=datos.index).dt.round("h").dt.hour
sunset_hour = pd.Series(sunset_hour, index=datos.index).dt.round("h").dt.hour
variables_solares = pd.DataFrame({
'sunrise_hour': sunrise_hour,
'sunset_hour': sunset_hour
})
variables_solares['daylight_hours'] = (
variables_solares['sunset_hour'] - variables_solares['sunrise_hour']
)
variables_solares["is_daylight"] = np.where(
(datos.index.hour >= variables_solares["sunrise_hour"])
& (datos.index.hour < variables_solares["sunset_hour"]),
1,
0,
)
# Variables basadas en festivos
# ==============================================================================
variables_festivos = datos[['Holiday']].astype(int)
variables_festivos['holiday_previous_day'] = variables_festivos['Holiday'].shift(24)
variables_festivos['holiday_next_day'] = variables_festivos['Holiday'].shift(-24)
# Variables basadas en temperatura
# ==============================================================================
wf_transformer = WindowFeatures(
variables = ["Temperature"],
window = ["1D", "7D"],
functions = ["mean", "max", "min"],
freq = "h",
)
variables_temp = wf_transformer.fit_transform(datos[['Temperature']])
# Unión de variables exógenas
# ==============================================================================
assert all(variables_calendario.index == variables_solares.index)
assert all(variables_calendario.index == variables_festivos.index)
assert all(variables_calendario.index == variables_temp.index)
variables_exogenas = pd.concat([
variables_calendario,
variables_solares,
variables_temp,
variables_festivos
], axis=1)
# Debido a la creación de medias móviles, hay valores faltantes al principio
# de la serie. Y debido a holiday_next_day hay valores faltantes al final.
variables_exogenas = variables_exogenas.iloc[7 * 24:, :]
variables_exogenas = variables_exogenas.iloc[:-24, :]
variables_exogenas.head(3)
Algunos aspectos del calendario, como las horas o los días, son cíclicos. Por ejemplo, la hora del día va de 0 a 23 horas. Aunque se interpreta como una variable continua, la hora 23:00 sólo dista una hora de las 00:00. Lo mismo ocurre con los meses del año, ya que diciembre sólo dista un mes de enero. El uso de funciones trigonométricas como seno y coseno permite representar patrones cíclicos y evitar incoherencias en la representación de los datos. Este enfoque se conoce como codificación cíclica y puede mejorar significativamente la capacidad predictiva de los modelos.
# Codificación cíclica de las variables de calendario y luz solar
# ==============================================================================
features_to_encode = [
"month",
"week",
"day_of_week",
"hour",
"sunrise_hour",
"sunset_hour",
]
max_values = {
"month": 12,
"week": 52,
"day_of_week": 6,
"hour": 23,
"sunrise_hour": 23,
"sunset_hour": 23,
}
cyclical_encoder = CyclicalFeatures(
variables = features_to_encode,
max_values = max_values,
drop_original = False
)
variables_exogenas = cyclical_encoder.fit_transform(variables_exogenas)
variables_exogenas.head(3)
En muchos casos, las variables exógenas no son independientes. Más bien, su efecto sobre la variable objetivo depende del valor de otras variables. Por ejemplo, el efecto de la temperatura en la demanda de electricidad depende de la hora del día. La interacción entre las variables exógenas puede captarse mediante nuevas variables que se obtienen multiplicando entre sí las variables existentes. Estas interacciones se obtienen fácilmente con la clase PolynomialFeatures de scikit-learn.
# Interacción entre variables exógenas
# ==============================================================================
transformer_poly = PolynomialFeatures(
degree = 2,
interaction_only = True,
include_bias = False
).set_output(transform="pandas")
poly_cols = [
'month_sin',
'month_cos',
'week_sin',
'week_cos',
'day_of_week_sin',
'day_of_week_cos',
'hour_sin',
'hour_cos',
'sunrise_hour_sin',
'sunrise_hour_cos',
'sunset_hour_sin',
'sunset_hour_cos',
'daylight_hours',
'is_daylight',
'holiday_previous_day',
'holiday_next_day',
'Temperature_window_1D_mean',
'Temperature_window_1D_min',
'Temperature_window_1D_max',
'Temperature_window_7D_mean',
'Temperature_window_7D_min',
'Temperature_window_7D_max',
'Temperature',
'Holiday'
]
variables_poly = transformer_poly.fit_transform(variables_exogenas[poly_cols])
variables_poly = variables_poly.drop(columns=poly_cols)
variables_poly.columns = [f"poly_{col}" for col in variables_poly.columns]
variables_poly.columns = variables_poly.columns.str.replace(" ", "__")
assert all(variables_exogenas.index == variables_poly.index)
variables_exogenas = pd.concat([variables_exogenas, variables_poly], axis=1)
variables_exogenas.head(3)
# Selección de variables exógenas incluidas en el modelo
# ==============================================================================
exog_features = []
# Columnas que terminan con _seno o _coseno son seleccionadas
exog_features.extend(variables_exogenas.filter(regex='_sin$|_cos$').columns.tolist())
# Columnas que empiezan con temp_ son seleccionadas
exog_features.extend(variables_exogenas.filter(regex='^Temperature_.*').columns.tolist())
# Columnas que empiezan con holiday_ son seleccionadas
exog_features.extend(variables_exogenas.filter(regex='^Holiday_.*').columns.tolist())
# Incluir temperatura y festivos
exog_features.extend(['Temperature', 'Holiday'])
# Combinar variables exógenas seleccionadas con la serie temporal en un único DataFrame
# ==============================================================================
datos = datos[['Demand']].merge(
variables_exogenas[exog_features],
left_index=True,
right_index=True,
how='inner' # Usar solo las filas que coinciden en ambos DataFrames
)
datos = datos.astype('float32')
# Split data into train-val-test
datos_train = datos.loc[: fin_train, :].copy()
datos_val = datos.loc[fin_train:fin_validacion, :].copy()
datos_test = datos.loc[fin_validacion:, :].copy()
Los hiperparámetros y lags identificados como óptimos en la sección anterior se utilizan de nuevo para entrenar el modelo, pero esta vez, las variables exógenas también se incluyen como predictores.
# Crear forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
regressor = LGBMRegressor(**best_params),
lags = best_lags,
window_features = window_features
)
# Backtesting
# ==============================================================================
metrica, predicciones = backtesting_forecaster(
forecaster = forecaster,
y = datos['Demand'],
exog = datos[exog_features],
cv = cv,
metric = 'mean_absolute_error',
n_jobs = 'auto',
verbose = False,
show_progress = True
)
display(metrica)
predicciones.head()
La inclusión de variables exógenas como predictores mejora aún más la capacidad predictiva del modelo.
Selección de predictores¶
La selección de predictores (feature selection) es el proceso de identificar un subconjunto de predictores relevantes para su uso en la creación del modelo. Es un paso importante en el proceso de machine learning, ya que puede ayudar a reducir el sobreajuste, mejorar la precisión del modelo y reducir el tiempo de entrenamiento. Dado que los regresores subyacentes de skforecast siguen la API de scikit-learn, es posible utilizar los métodos de selección de predictores disponibles en scikit-learn de forma sencilla con la función select_features().
Dos de los métodos más populares son Recursive Feature Elimination y Sequential Feature Selection.
💡 Tip
La selección de predictores es una herramienta potente para mejorar el rendimiento de los modelos de machine learning. Sin embargo, es computacionalmente costosa y puede requerir mucho tiempo. Dado que el objetivo es encontrar el mejor subconjunto de predictores, no el mejor modelo, no es necesario utilizar todos los datos disponibles ni un modelo muy complejo. En su lugar, se recomienda utilizar un pequeño subconjunto de los datos y un modelo sencillo. Una vez identificados los mejores predictores, el modelo puede entrenarse utilizando todo el conjunto de datos y una configuración más compleja.
# Crear forecaster
# ==============================================================================
regressor = LGBMRegressor(
n_estimators = 100,
max_depth = 5,
random_state = 15926,
verbose = -1
)
forecaster = ForecasterRecursive(
regressor = regressor,
lags = 24,
window_features = window_features
)
# Eliminación recursiva de predictores con validación cruzada
# ==============================================================================
selector = RFECV(
estimator = regressor,
step = 1,
cv = 3,
n_jobs = -1
)
lags_select, window_features_select, exog_select = select_features(
forecaster = forecaster,
selector = selector,
y = datos_train['Demand'],
exog = datos_train[exog_features],
select_only = None,
force_inclusion = None,
subsample = 0.5, # Muestreo para acelerar el cálculo
random_state = 123,
verbose = True,
)
El RFECV de scikit-learn empieza entrenando un modelo con todos los predictores disponibles y calculando la importancia de cada uno en base a los atributos como coef_ o feature_importances_. A continuación, se elimina el predictor menos importante y se realiza una validación cruzada para calcular el rendimiento del modelo con los predictores restantes. Este proceso se repite hasta que la eliminación de predictores adicionales no mejora la metrica de rendimiento elegida o se alcanza el min_features_to_select. El resultado final es un subconjunto de predictores que idealmente equilibra la simplicidad del modelo y su capacidad predictiva, determinada por el proceso de validación cruzada.
El forecater se entrena y reevalúa utilizando solo el conjunto de predictores seleccionados.
# Crear forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
regressor = LGBMRegressor(**best_params),
lags = lags_select,
window_features = window_features
)
# Backtesting con los predictores seleccionados y los datos de test
# ==============================================================================
metrica, predicciones = backtesting_forecaster(
forecaster = forecaster,
y = datos['Demand'],
exog = datos[exog_select],
cv = cv,
metric = 'mean_absolute_error',
n_jobs = 'auto',
verbose = False,
show_progress = True
)
metrica
Se ha conseguido reducir el número de predictores, sin que el rendimiento del modelo no se ve comprometido. Esto permite simplificar el modelo y acelera el entrenamiento. Además, se reduce el riesgo de sobreajuste porque es menos probable que el modelo aprenda ruido de características irrelevantes.
Forecasting probabilístico: Intervalos de predicción¶
Un intervalo de predicción define el intervalo dentro del cual es de esperar que se encuentre el verdadero valor de la variable respuesta con una determinada probabilidad. Rob J Hyndman y George Athanasopoulos, listan en su libro Forecasting: Principles and Practice mútiples formas de estimar intervalos de predicción, la mayoría los cuales requieren que los resudios (errores) del modelo se distribuyan de forma normal. Cuando no se puede asumir esta propiedad, se puede recurrir a bootstrapping, que solo asume que los residuos no están correlacionados. Este es uno de los métodos disponibles en skforecast. Se pude encontrar una explicación más detallada de los intervalos de predicción en Probabilistic forecasting: prediction intervals and prediction distribution.
El siguiente código muestra cómo generar intervalos de predicción con un modelo autorregresivo. La función prediction_interval() se utiliza para estimar los intervalos para cada step predicho. Después, se utiliza la función backtesting_forecaster() para generar los intervalos de predicción de todo el conjunto de test. El argumento interval se utiliza para especificar la probabilidad de cobertura deseada de los intervalos. En este caso, interval se establece en [5, 95], lo que significa que los intervalos se calculan con los percentiles 5 y 95, lo que da como resultado una cobertura teórica del 90%. El argumento n_boot se utiliza para especificar el número de iteraciones de bootstraping que se utilizan para estimar los intervalos. Cuanto mayor sea el número de muestras, más precisos serán los intervalos de predicción, pero más tiempo tardará el proceso.
# Crear y entrenar el forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
regressor = LGBMRegressor(**best_params),
lags = lags_select,
window_features = window_features,
binner_kwargs = {"n_bins": 25}
)
forecaster.fit(
y = datos.loc[:fin_train, 'Demand'],
exog = datos.loc[:fin_train, exog_select]
)
# Predecir intervalos
# ==============================================================================
# Dado que el modelo ha sido entrenado con variables exógenas, estas deben ser
# proporcionadas también en la predicción.
predicciones = forecaster.predict_interval(
exog = datos.loc[fin_train:, exog_select],
steps = 24,
interval = [5, 95],
)
predicciones.head()
Por defecto, los intervalos se calculan utilizando los residuos in-sample (residuos del conjunto de entrenamiento). Sin embargo, esto puede dar lugar a intervalos demasiado estrechos (demasiado optimistas). Para evitarlo, se utiliza el método set_out_sample_residuals() para almacenar residuos out-sample calculados mediante backtesting con un conjunto de validación.
Si además de los residuos, se le pasan las correspondientes predicciones al método set_out_sample_residuals(), entonces los residuos utilizados en el proceso de bootstrapping se seleccionan condicionados al rango de valores de las predicciones. Esto puede ayudar a conseguir intervalos con mayor covertura a la vez que se mantienen lo más estrechos posibles.
# Backtesting sobre los datos de validación para obtener los residuos out-sample
# ==============================================================================
cv = TimeSeriesFold(
steps = 24,
initial_train_size = len(datos.loc[:fin_train]),
refit = False,
)
_, predicciones_val = backtesting_forecaster(
forecaster = forecaster,
y = datos.loc[:fin_validacion, 'Demand'], # Train + Validation
exog = datos.loc[:fin_validacion, exog_select],
cv = cv,
metric = 'mean_absolute_error',
n_jobs = 'auto',
verbose = False,
show_progress = True
)
# Distribución residuos Out-sample
# ==============================================================================
residuos = datos.loc[predicciones_val.index, 'Demand'] - predicciones_val['pred']
print(pd.Series(np.where(residuos < 0, 'negative', 'positive')).value_counts())
plt.rcParams.update({'font.size': 8})
_ = plot_residuals(residuals=residuos, figsize=(7, 4))
# Almacenar residuos out-sample en el forecaster
# ==============================================================================
forecaster.set_out_sample_residuals(
y_true = datos.loc[predicciones_val.index, 'Demand'],
y_pred = predicciones_val['pred']
)
A continuación, se ejecuta el proceso de backtesting para estimar los intervalos de predicción en el conjunto de test. Se indica el argumento use_in_sample_residuals en False para que se utilicen los residuos out-sample almacenados previamente y use_binned_residuals para que el los residuos utilizados en el bootstrapping se seleccionen condicionados al rango de valores de las predicciones.
# Backtest con intervalos de predicción para el conjunto de test utilizando los
# residuos out-sample
# ==============================================================================
cv = TimeSeriesFold(
steps = 24,
initial_train_size = len(datos.loc[:fin_validacion]),
refit = False,
)
metrica, predicciones = backtesting_forecaster(
forecaster = forecaster,
y = datos['Demand'],
exog = datos[exog_select],
cv = cv,
metric = 'mean_absolute_error',
interval = [5, 95],
n_boot = 200,
use_in_sample_residuals = False, # Se utilizan los residuos out-sample
use_binned_residuals = True, # Residuos condicionados a los valores predichos
n_jobs = 'auto',
verbose = False,
show_progress = True
)
predicciones.head(5)
# Gráfico intervalos de predicción vs valores reales
# ==============================================================================
fig = go.Figure([
go.Scatter(
name='Predicción', x=predicciones.index, y=predicciones['pred'], mode='lines',
),
go.Scatter(
name='Valor real', x=datos_test.index, y=datos_test['Demand'], mode='lines',
),
go.Scatter(
name='Upper Bound', x=predicciones.index, y=predicciones['upper_bound'],
mode='lines', marker=dict(color="#444"), line=dict(width=0), showlegend=False
),
go.Scatter(
name='Lower Bound', x=predicciones.index, y=predicciones['lower_bound'],
marker=dict(color="#444"), line=dict(width=0), mode='lines',
fillcolor='rgba(68, 68, 68, 0.3)', fill='tonexty', showlegend=False
)
])
fig.update_layout(
title="Predicción con intervalos de confianza vs valor real",
xaxis_title="Fecha",
yaxis_title="Demanda (MWh)",
width=750,
height=370,
margin=dict(l=20, r=20, t=35, b=20),
hovermode="x",
legend=dict(orientation="h", yanchor="top", y=1.01, xanchor="left", x=0.01)
)
fig.show()
# Cobertura del intervalo predicho
# ==============================================================================
dentro_intervalo = np.where(
(datos.loc[fin_validacion:, 'Demand'] >= predicciones['lower_bound'])
& (datos.loc[fin_validacion:, 'Demand'] <= predicciones['upper_bound']),
True,
False
)
cobertura = dentro_intervalo.mean()
area = (predicciones['upper_bound'] - predicciones['lower_bound']).sum()
print(f"Área total del intervalo: {round(area, 2)}")
print(f"Cobertura del intervalo predicho: {round(100 * cobertura, 2)} %")
La cobertura observada de los intervalos es superior a la cobertura teórica esperada (90%), los intervalos son más conservadores de lo nesario. Esto significa que contienen el valor real con mayor probabilidad de la esperada.
✎ Nota
Para información detallada de las funcionalidades de forecasting probabilístico ofrecidas por skforecast visitar: Forecasting probabilístico con machine learning.Explicabilidad del modelo¶
Debido a la naturaleza compleja de muchos de los actuales modelos de machine learning, a menudo funcionan como cajas negras, lo que dificulta entender por qué han hecho una predicción u otra. Las técnicas de explicabilidad pretenden desmitificar estos modelos, proporcionando información sobre su funcionamiento interno y ayudando a generar confianza, mejorar la transparencia y cumplir los requisitos normativos en diversos ámbitos. Mejorar la explicabilidad de los modelos no sólo ayuda a comprender su comportamiento, sino también a identificar sesgos, mejorar su rendimiento y permitir a las partes interesadas tomar decisiones más informadas basadas en los conocimientos del machine learning
Skforecast es compatible con algunos de los métodos de explicabilidad más populares: model-specific feature importances, SHAP values, and partial dependence plots.
# Crear y entrenar el forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
regressor = LGBMRegressor(**best_params),
lags = lags_select,
window_features = window_features
)
forecaster.fit(
y = datos.loc[:fin_validacion, 'Demand'],
exog = datos.loc[:fin_validacion, exog_select]
)
Explicabilidad propia del modelo¶
La explicabilidad propia del modelo se refiere a la capacidad inherente de un modelo para ser interpretado y comprendido sin la necesidad de técnicas adicionales.
# Importancia de los predictores en el modelo
# ==============================================================================
feature_importances = forecaster.get_feature_importances()
feature_importances.head(10)
⚠ Warning
El métodoget_feature_importances() sólo devuelve valores si el regresor del forecaster tiene el atributo coef_ o feature_importances_, que son los estándares en scikit-learn.
Shap values¶
Los valores SHAP (SHapley Additive exPlanations) son un método muy utilizado para explicar los modelos de machine learning, ya que ayudan a comprender cómo influyen las variables y los valores en las predicciones de forma visual y cuantitativa.
Se puede obtener un análisis SHAP a partir de modelos skforecast con sólo dos elementos:
El regresor interno del forecaster.
Las matrices de entrenamiento creadas a partir de la serie temporal y variables exógenas, utilizadas para ajustar el pronosticador.
Aprovechando estos dos componentes, los usuarios pueden crear explicaciones interpretables para sus modelos de skforecast. Estas explicaciones pueden utilizarse para verificar la fiabilidad del modelo, identificar los factores más significativos que contribuyen a las predicciones y comprender mejor la relación subyacente entre las variables de entrada y la variable objetivo.
# Matrices de entrenamiento utilizadas por el forecaster para ajustar el regresor interno
# ==============================================================================
X_train, y_train = forecaster.create_train_X_y(
y = datos_train['Demand'],
exog = datos_train[exog_select]
)
display(X_train.head(3))
display(y_train.head(3))
# Crear SHAP explainer (para modelos basados en árboles)
# ==============================================================================
shap.initjs()
explainer = shap.TreeExplainer(forecaster.regressor)
# Se selecciona una muestra del 50% de los datos para acelerar el cálculo
rng = np.random.default_rng(seed=785412)
sample = rng.choice(X_train.index, size=int(len(X_train)*0.5), replace=False)
X_train_sample = X_train.loc[sample, :]
shap_values = explainer.shap_values(X_train_sample)
✎ Note
La librería Shap cuenta con varios Explainers, cada uno diseñado para un tipo de modelo diferente. Elshap.TreeExplainer explainer se utiliza para modelos basados en árboles, como el LGBMRegressor utilizado en este ejemplo. Para más información, consultar la documentación de SHAP.
# Shap summary plot (top 10)
# ==============================================================================
shap.summary_plot(shap_values, X_train_sample, max_display=10, show=False)
fig, ax = plt.gcf(), plt.gca()
ax.set_title("SHAP Summary plot")
ax.tick_params(labelsize=8)
fig.set_size_inches(8, 4.5)
# Force plot para la primera observación de la muestra
# ==============================================================================
shap.force_plot(explainer.expected_value, shap_values[0,:], X_train_sample.iloc[0,:])
Forecaster direct multi-step¶
Los modelos ForecasterRecursive y ForecasterRecursiveCustom siguen una estrategia recursiva en la que cada nueva predicción se basa en las anteriores. Otra estrategia para predecir múltiples valores futuros consiste en entrenar un modelo diferente para cada paso (step) a predecir. Esto se conoce como direct multi-step forecasting y, aunque es más costosa computacionalmente que la estrategia recursiva debido a la necesidad de entrenar múltiples modelos, puede dar mejores resultados.
# Forecaster con le método direct
# ==============================================================================
forecaster = ForecasterDirect(
regressor = LGBMRegressor(**best_params),
steps = 24,
lags = lags_select,
window_features = window_features
)
# Backtesting
# ==============================================================================
metrica, predicciones = backtesting_forecaster(
forecaster = forecaster,
y = datos['Demand'],
exog = datos[exog_select],
cv = cv,
metric = 'mean_absolute_error',
n_jobs = 'auto',
verbose = False,
show_progress = True
)
display(metrica)
predicciones.head()
El modelo direct multi-step supera la capacidad de predicción del modelo recursivo, reduciendo aún más el error medio absoluto. Sin embargo, es importante tener en cuenta su mayor coste computacional a la hora de evaluar si merece la pena aplicarlo.
Predicción diaria anticipada¶
En el apartado anterior, se evaluó el modelo asumiendo que las predicciones del día siguiente se ejecutan justo al final del día anterior. En la práctica, esto no resulta muy útil ya que, para las primeras horas del día, apenas se dispone de anticipación.
Supóngase ahora que, para poder tener suficiente margen de acción, a las 11:00 horas de cada día se tienen que generar las predicciones del día siguiente. Es decir, a las 11:00 del dia $D$ se tienen que predecir las horas [12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23] de ese mismo día, y las horas [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23] del día $D+1$. Esto implica que se tienen que predecir un total de 36 horas a futuro aunque solo se almacenen las 24 últimas.
Este tipo de evaluación puede realizarse mediante la función backtesting_forecaster() y su parámetro gap. Además, el parámetro allow_incomplete_fold permite excluir la última iteración del análisis si no tiene el mismo tamaño que el número de steps requeridos. El proceso adaptado a este escenario se ejecuta diariamente y consta de los siguientes pasos:
A las 11:00h del primer día del conjunto de test, se predicen las 36 horas siguientes (las 12 horas que quedan del día más las 24 horas del día siguiente).
Se almacenan solo las predicciones del día siguiente, es decir, las 24 últimas.
Se añaden los datos de test hasta las 11:00 del día siguiente.
Se repite el proceso.
De esta forma, a las 11:00 de cada día, el modelo tiene acceso a los valores reales de demanda registrados hasta ese momento.
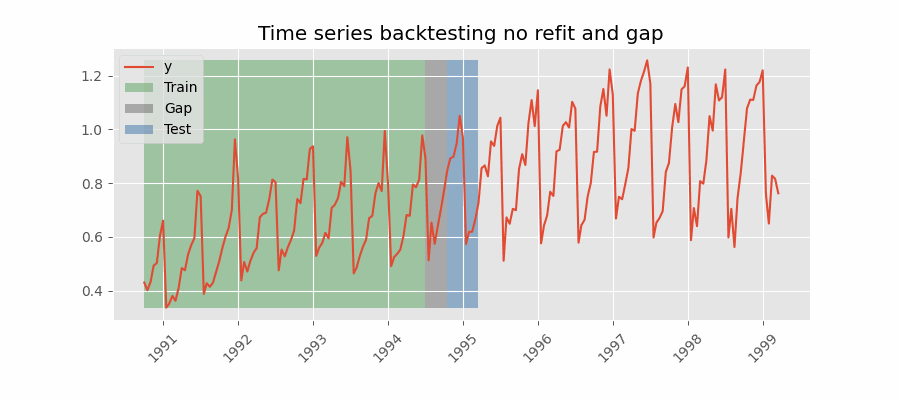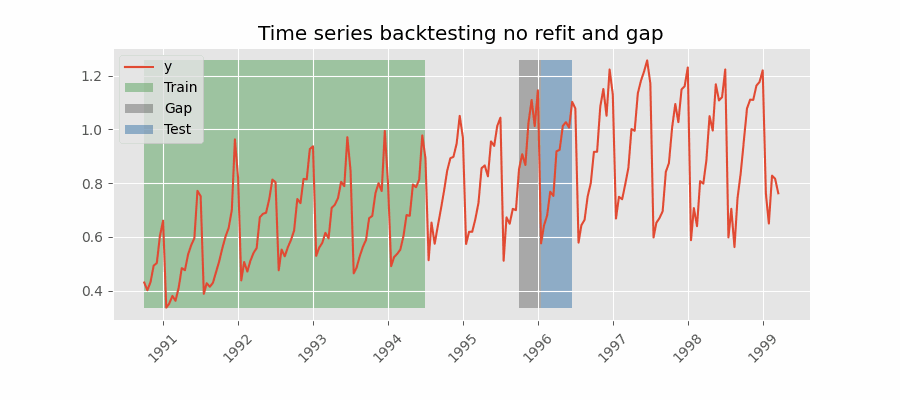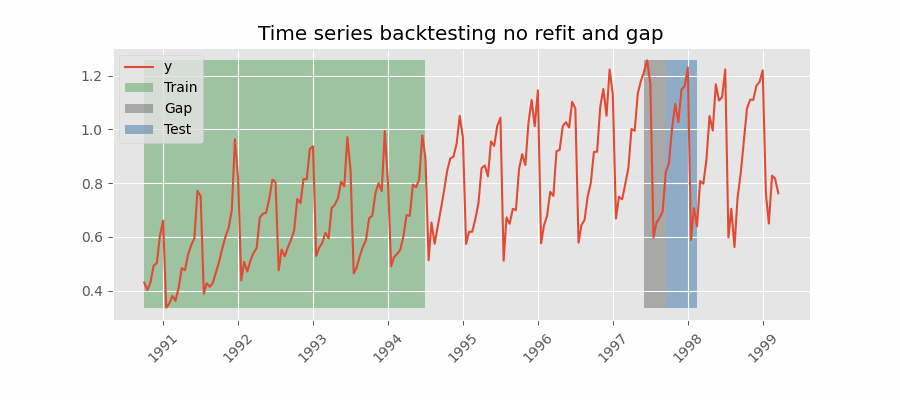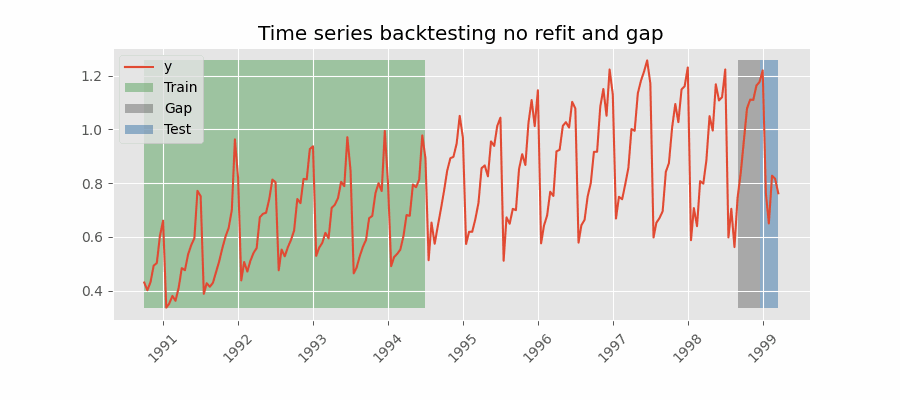
⚠ Warning
Se deben tener en cuenta las siguientes consideraciones:- Los datos de entrenamiento deben terminar donde empieza el gap. En este caso, el
initial_train_sizedebe ampliarse en 12 posiciones para que el primer punto a predecir sea el 2014-12-01 12:00:00. - En este ejemplo, aunque sólo se almacenan las últimas 24 predicciones (steps) para la evaluación del modelo, el número total de pasos predichos en cada iteración es de 36 (steps + gap).
# Final de initial_train_size + 12 posiciones
# ==============================================================================
datos.iloc[:len(datos.loc[:fin_validacion]) + 12].tail(2)
# Forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
regressor = LGBMRegressor(**best_params),
lags = lags_select,
window_features = window_features
)
# Backtesting con gap
# ==============================================================================
cv = TimeSeriesFold(
steps = 24,
initial_train_size = len(datos.loc[:fin_validacion]) + 12,
refit = False,
gap = 12,
)
metrica, predicciones = backtesting_forecaster(
forecaster = forecaster,
y = datos['Demand'],
exog = datos[exog_select],
cv = cv,
metric = 'mean_absolute_error',
n_jobs = 'auto',
verbose = False,
show_progress = True
)
display(metrica)
predicciones.head(5)
Como era de esperar, el error aumenta a medida que el horizonte de previsión pasa de 24 a 36 horas.
Conclusiones¶
El uso de modelos de gradient boosting ha demostrado ser una potente herramienta para predecir la demanda de energía. Una de las principales ventajas de estos modelos es que pueden incorporar fácilmente variables exógenas, lo que puede mejorar significativamente el poder predictivo del modelo. Además, el uso de técnicas de explicabilidad puede ayudar a comprender visual y cuantitativamente cómo afectan las variables y los valores a las predicciones. Todas estas cuestiones se abordan fácilmente con la biblioteca skforecast.
| Forecaster | Exogenous Variables | MAE backtest |
|---|---|---|
ForecasterEquivalentDate (Baseline) |
False | 308.3 |
ForecasterRecursive |
False | 206.3 |
ForecasterRecursive |
True | 135.2 |
ForecasterRecursive |
True (Feature Selection) | 133.3 |
ForecasterDirect |
True (Feature Selection) | 119.8 |
Información de sesión¶
import session_info
session_info.show(html=False)
Bibliografía¶
Hyndman, R.J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia.
Time Series Analysis and Forecasting with ADAM Ivan Svetunkov
Joseph, M. (2022). Modern time series forecasting with Python: Explore industry-ready time series forecasting using modern machine learning and Deep Learning. Packt Publishing.
Instrucciones para citar¶
Cómo citar este documento
Si utiliza este documento o parte de él, por favor, cite la fuente, ¡gracias!
Predicción (forecasting) de la demanda energética con machine learning por Joaquín Amat Rodrigo y Javier Escobar Ortiz, disponible con licencia Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0 DEED) at https://www.cienciadedatos.net/documentos/py29-forecasting-demanda-energia-electrica-python.html
Cómo citar skforecast
Si utiliza skforecast, le agradecemos que cite el software publicado.
Zenodo:
Amat Rodrigo, Joaquin, & Escobar Ortiz, Javier. (2023). skforecast (v0.14.0). Zenodo. https://doi.org/10.5281/zenodo.8382788
APA:
Amat Rodrigo, J., & Escobar Ortiz, J. (2023). skforecast (Version 0.14.0) [Computer software]. https://doi.org/10.5281/zenodo.8382788
BibTeX:
@software{skforecast, author = {Amat Rodrigo, Joaquin and Escobar Ortiz, Javier}, title = {skforecast}, version = {0.14.0}, month = {11}, year = {2024}, license = {BSD-3-Clause}, url = {https://skforecast.org/}, doi = {10.5281/zenodo.8382788} }
¿Te ha gustado el artículo? Tu ayuda es importante
Mantener un sitio web tiene unos costes elevados, tu contribución me ayudará a seguir generando contenido divulgativo gratuito. ¡Muchísimas gracias! 😊
Este documento creado por Joaquín Amat Rodrigo y Javier Escobar Ortiz tiene licencia Attribution-NonCommercial-ShareAlike 4.0 International.
Se permite:
-
Compartir: copiar y redistribuir el material en cualquier medio o formato.
-
Adaptar: remezclar, transformar y crear a partir del material.
Bajo los siguientes términos:
-
Atribución: Debes otorgar el crédito adecuado, proporcionar un enlace a la licencia e indicar si se realizaron cambios. Puedes hacerlo de cualquier manera razonable, pero no de una forma que sugiera que el licenciante te respalda o respalda tu uso.
-
NoComercial: No puedes utilizar el material para fines comerciales.
-
CompartirIgual: Si remezclas, transformas o creas a partir del material, debes distribuir tus contribuciones bajo la misma licencia que el original.