Más sobre ciencia de datos: cienciadedatos.net

Introducción¶
Un paso esencial en el desarrollo de modelos de machine learning consiste en seleccionar las variables más predictivas del conjunto de datos. Pero, ¿cómo hacerlo? Eso es lo que te voy a contar en este artículo.
Existen varios métodos de selección de variables. En machine learning, estos métodos se clasifican tradicionalmente en 3 grupos:
Métodos de filtro (del inglés, filter methods)
Métodos integrados (del inglés, embedded methods)
Métodos de envoltura (del inglés, wrapper methods)
Todos los métodos de selección de variables tienen sus ventajas y limitaciones. Por ejemplo, los métodos de filtro son óptimos para sets de datos gigantes, pero no tienen en cuenta la interacción entre variables o las características del modelo de machine learning. Otros métodos, como los de envoltura, tienen un costo computacional extremadamente alto, y por lo tanto, solo son aplicables a conjuntos de datos relativamente pequeños. Y hay métodos, claro, que se encuentran en un punto intermedio.
Además de existir diferentes métodos, también hay diferentes implementaciones de estos algoritmos en librerías de código abierto de Python.
Cubrir todos los métodos, o todas las implementaciones, en un artículo es una misión imposible. Para esto, escribí el libro Feature Selection in Machine Learning (por ahora solo disponible en inglés). En este artículo, en cambio, voy a presentarte los mecanismos comunes de los diferentes métodos de selección. Luego voy a contarte en mas detalle los métodos mas utilizados de cada grupo. Para terminar, te voy a mostrar como se usan las librerias de Python para selección de variables, destacando qué métodos de selección están disponibles en cada una.
¡Empecemos!
Métodos de selección de variables¶
Cuando seleccionamos variables, lo que hacemos es elegir un subconjunto de variables del conjunto de datos inicial, y vamos a utilizar este subconjunto para entrenar los algoritmos de machine learning. Al reducir el número de variables, podemos mejorar el rendimiento de los modelos, por ejemplo, evitando el sobreajuste, reducir el tiempo de entrenamiento y de predicción, y crear modelos más interpretables.
Tradicionalmente, los métodos de selección se han agrupado en tres categorías principales: métodos de filtro, métodos de envoltura (wrapper) y métodos integrados (embedded).

Así que a continuación, te cuento un poco más de qué se trata cada grupo.
Métodos de filtro¶
Los métodos de filtro eligen variables basándose exclusivamente en sus propiedades, e ignorando su interacción con el modelo de machine learning y con otras variables. Estos métodos primero le asignan un ranking a cada variable, y luego eligen las mejores ranqueadas.
Para asignar un ranking a cada variable, se pueden usar diferentes procedimientos estadísticos, como el test de chi-cuadrado, ANOVA, correlación o información mutua. Y también se pueden utilizar procedimientos más simples, como evaluar la variabilidad o cardinalidad de la variable.
Luego del ranking, se procede a elegir las variables mejor clasificadas. Para esto, se pueden elegir arbitrariamente las mejores X variables, donde X es un numero arbitrario, o las variables en el percentilo superior.
Si el ranking consiste en un valor de probabilidad, por ejemplo, aquel retornado por los tests estadísticos que mencioné previamente, entonces también podemos usar un "alfa" estadístico, que es un valor de probabilidad, típicamente 0,05, y seleccionar aquellas variables cuyo ranking es menor que dicho alfa.
Métodos de envoltura (wrapper)¶
Los métodos de envoltura "envuelven" al modelo predictivo en un algoritmo de búsqueda. ¿Qué significa esto? Que utilizan al modelo predictivo para asignar un valor o un ranking a subconjuntos de variables. Y luego, eligen el subconjunto que mejor rendimiento genera.
Los métodos de envoltura funcionan así: primero generan múltiples subconjuntos de variables. Luego entrenan el modelo de machine learning utilizando cada uno de estos subconjuntos y evalúan su rendimiento. Luego eligen el subconjunto que produjo el mejor modelo. ¡Fácil!
Los diferentes métodos en este grupo se diferencian entonces en cómo forman estos diferentes subconjuntos de datos.
El algoritmo de forward search o búsqueda progresiva genera subconjuntos agregando de a una variable en cada instancia. El algoritmo de backward search o eliminación progresiva elimina de a una variable a la vez. Y el algoritmo de búsqueda exhaustiva forma todos los subconjuntos de datos posibles dado un set de datos inicial.
Métodos integrados (embedded)¶
Los métodos integrados "integran" el procedimiento de selección en el entrenamiento del modelo predictivo. Lasso y la importancia de variables derivada de árboles de decisión son ejemplos clásicos de métodos integrados.
Lasso asigna un valor a los coeficientes de regresión de los modelos lineales, y si este valor es 0, entonces podemos eliminar dichas variables. Asimismo, podemos utilizar la importancia derivada de árboles de decisión para ranquear y luego elegir las variables más predictivas.
Librerías para selección de variables¶
Existen 3 librerías de Python con módulos para selección de variables:
- Scikit-learn
- MLXtend
- Feature-engine
Scikit-learn es probablemente la mas usada, pero Feature-engine es la mas completa.
🔹 Scikit-learn incluye algoritmos para:
- Métodos de filtro
- Métodos de envoltura (wrapper)
- Métodos integrados (embedded)
- Eliminación recursiva de variables (Recursive Feature Elimination)
🔹 MLXtend ofrece algoritmos para implementar:
- Búsqueda progresiva (forward selection)
- Eliminación progresiva (backward selection)
- Búsqueda exhaustiva (exhaustive search)
🔹 Feature-engine proporciona métodos alternativos basados en:
- Métodos de filtro basados en cardinalidad
- Correlación y duplicación
- Rendimiento de modelos de machine learning
- Permutación de variables (feature shuffling)
- Métodos estadísticos como la ganancia de información o el PSI.
En la siguiente tabla te muestro una comparación de los algoritmos que soportan las diferentes librerías:
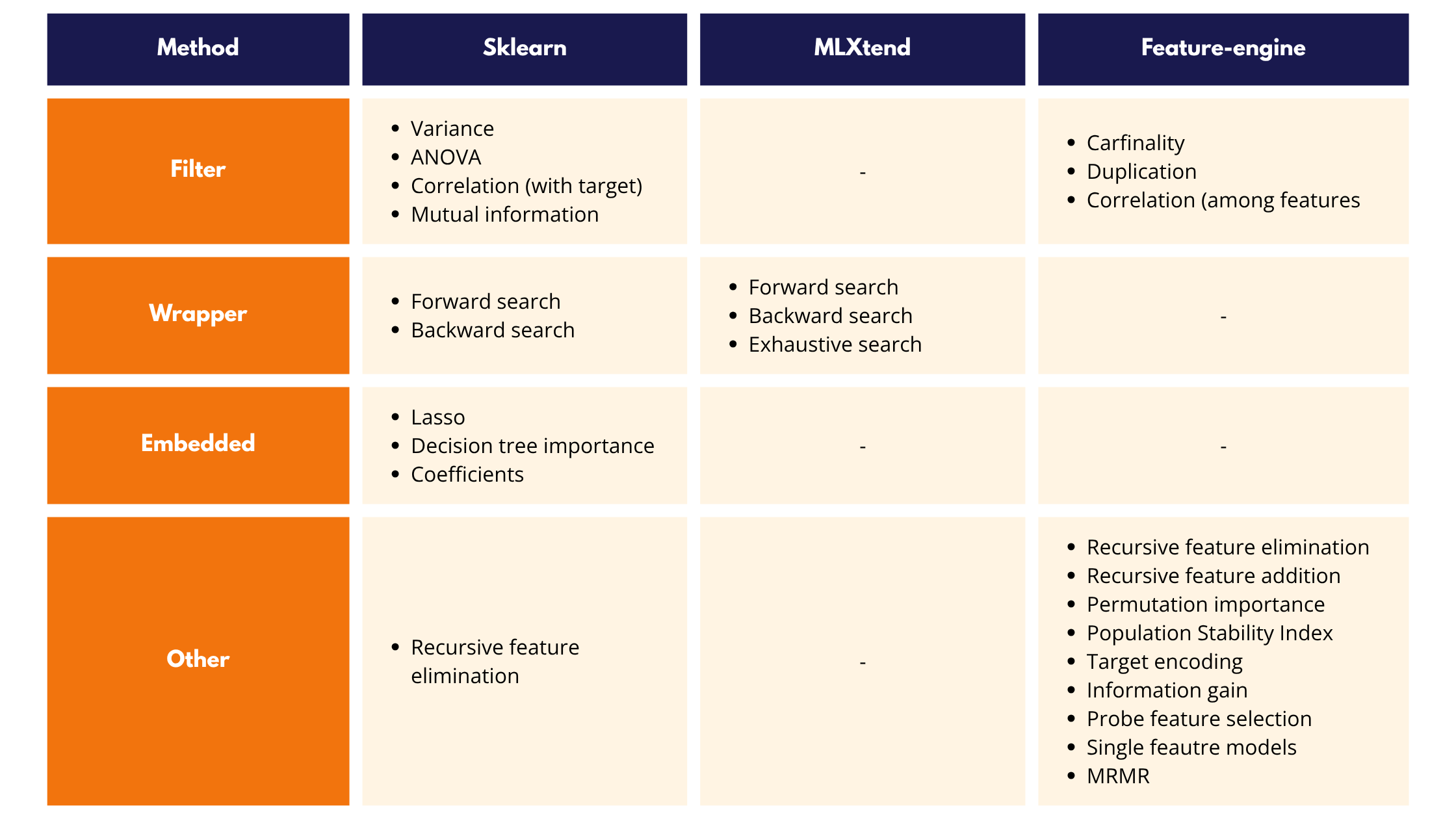
A continuación, vamos a implementar varias técnicas de selección de variables con Scikit-learn y Feature-engine.
Selección de variables con Scikit-learn¶
Scikit-learn tiene algoritmos para métodos de filtro, envoltura e integrados, e incluye también la eliminación recursiva de variables.
Entre los métodos de filtro, podemos seleccionar características basándonos en la varianza de la variable o utilizando ANOVA, como muestro a continuación.
Selección por varianza¶
Con Scikit-learn, podemos eliminar variables irrelevantes analizando su variabilidad. Las variables cuya desviación estándar es cero son constantes y, por lo tanto, podemos eliminarlas.
Para esta demo, voy a crear un dataset con 10 variables, 3 de las cuales son constantes, y luego las voy a eliminar usando Scikit-learn:
## Librerias y funciones.
import pandas as pd
from sklearn.datasets import make_classification
from sklearn.feature_selection import VarianceThreshold
# Set de datos con 10 variables, 3 de las cuales son constantes.
X, y = make_classification(
n_samples=1000,
n_features=10,
n_classes=2,
random_state=10,
)
X = pd.DataFrame(X)
X[[0, 5, 9]] = 1
# Eliminar variables constantes
sel = VarianceThreshold(threshold=0)
X_t = sel.fit_transform(X)
En el código anterior, primero configuramos el transformador para eliminar variables constantes y, a continuación, aplicamos el método fit, seguido de transform. El VarianceThreshold encontró las variables constantes utilizando fit(). Con transform(), las eliminó de los datos. Entonces X_t contiene variables cuya variabilidad es mayor que 0.
ANOVA¶
ANOVA es un test estadístico adecuado para seleccionar variables continuas cuando la variable objetivo es categórica. Vamos a explorar cómo seleccionar variables utilizando ANOVA y Scikit-learn. Utilizaremos el conjunto de datos de cáncer de mama.
## Librerias y funciones.
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.feature_selection import SelectKBest, f_classif
from sklearn.model_selection import train_test_split
# Cargar dataset
breast_cancer = load_breast_cancer()
X = pd.DataFrame(breast_cancer.data, columns=breast_cancer.feature_names)
y = breast_cancer.target
# Separar dataset en conjunto de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# Ranquear y seleccionar variables segun ANOVA
sel = SelectKBest(score_func = f_classif, k=10).fit(X_train, y_train)
# Eliminar variables no seleccionadas
X_train_t = sel.transform(X_train)
X_test_t = sel.transform(X_test)
Con SelectKBest indicamos el número de variables que queremos seleccionar. Generalmente es un valor arbitrario, pero podemos optimizarlo con validación cruzada. f_classif es la función de scikit-learn que implementa ANOVA.
Regularización Lasso¶
Lasso puede reducir algunos de los coeficientes de un modelo lineal a 0. Esto significa que estas variables no son predictivas y podemos eliminarlas. Aquí, te muestro cómo seleccionar variables utilizando Lasso en un conjunto de datos de regresión.
## Librerias y funciones.
import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer, fetch_california_housing
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import Lasso, LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
A continuación importaremos el conjunto de datos de cáncer de mama de Scikit-learn con el objetivo de predecir si un tumor es benigno o maligno. Se trata de un conjunto de datos de clasificación. Luego, dividimos los datos en un conjunto de entrenamiento y otro de prueba:
# Cargar dataset
breast_cancer = load_breast_cancer()
X = pd.DataFrame(breast_cancer.data, columns=breast_cancer.feature_names)
y = breast_cancer.target
# Separar dataset en conjunto de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Vamos a configurar el escalador estándar de Scikit-learn:
scaler = StandardScaler()
scaler.fit(X_train)
StandardScaler()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
StandardScaler()
A continuación, seleccionaremos las variables utilizando la regresión logística con la regularización Lasso:
selector = SelectFromModel(
LogisticRegression(C=0.5, penalty='l1', solver='liblinear', random_state=10))
selector.fit(scaler.transform(X_train), y_train)
SelectFromModel(estimator=LogisticRegression(C=0.5, penalty='l1',
random_state=10,
solver='liblinear'))In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
SelectFromModel(estimator=LogisticRegression(C=0.5, penalty='l1',
random_state=10,
solver='liblinear'))LogisticRegression(C=0.5, penalty='l1', random_state=10, solver='liblinear')
LogisticRegression(C=0.5, penalty='l1', random_state=10, solver='liblinear')
Ejecutando selector.get_support() obtenemos un vector booleano con True para las variables que tienen coeficientes distintos de cero:
selector.get_support()
array([False, True, False, False, False, False, False, True, True,
False, True, False, False, False, False, True, False, False,
False, True, True, True, True, True, True, False, True,
True, True, False])
Podemos identificar así los nombres de las variables que se eliminarán:
removed_feats = X_train.columns[(selector.estimator_.coef_ == 0).ravel().tolist()]
removed_feats
Index(['mean radius', 'mean perimeter', 'mean area', 'mean smoothness',
'mean compactness', 'mean concavity', 'mean fractal dimension',
'texture error', 'perimeter error', 'area error', 'smoothness error',
'concavity error', 'concave points error', 'symmetry error',
'worst compactness', 'worst fractal dimension'],
dtype='object')
Podemos eliminar las variables de los conjuntos de entrenamiento y prueba de la siguiente manera:
X_train_selected = selector.transform(scaler.transform(X_train))
X_test_selected = selector.transform(scaler.transform(X_test))
Cambia el valor de la penalización (C) para ver si cambia el resultado. El mejor valor de C, y por tanto, el mejor subconjunto de características, puede determinarse con validación cruzada.
Eliminación recursiva de variables¶
La eliminación recursiva de variables es un proceso secuencial en el que se elimina una variable en cada iteración, y la importancia de las variables se vuelve a evaluar después de cada eliminación.
En Scikit-learn, podemos implementar la eliminación recursiva de características con el RFE o RFECV.
Vamos a seleccionar variables recursivamente utilizando la importancia derivada del modelo de random forest. Utilizaremos el conjunto de datos de cáncer de mama, y separaremos los datos en un conjunto de datos de entrenamiento y un conjunto de datos de prueba.
## Librerias y funciones.
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import RFE
from sklearn.model_selection import train_test_split
# Cargar dataset
breast_cancer = load_breast_cancer()
X = pd.DataFrame(breast_cancer.data, columns=breast_cancer.feature_names)
y = breast_cancer.target
# Separar dataset en conjunto de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# Especificar el modelo de random forest
clf = RandomForestClassifier(n_estimators=10, random_state=10)
# Eliminacion recursiva
sel_ = RFE(
clf,
n_features_to_select=8,
step=2,
)
sel_.fit(X_train, y_train)
# Eliminar variables de los conjuntos de datos
X_train_selected = sel_.transform(X_train)
X_test_selected = sel_.transform(X_test)
Aquí, RFE entrena un random forest con todas las variables, y luego remueve la variable menos importante. A continuación, entrena otro random forest con las variables restantes y remueve la más importante, y así sucesivamente, hasta obtener un set de datos de 8 variables en nuestro caso.
Selección de variables con Feature-engine¶
Feature-engine contiene algoritmos para seleccionar variables basadas en la eliminación o adición recursiva, permutación de variables, índice de estabilidad de población, valor medio de la variable respuesta, cardinalidad y más. Consulta la documentación de Feature-engine para obtener más información.
En este artículo te muestro cómo seleccionar variables basándonos en modelos de una sola variable y en correlación.
Modelos de una sola variable¶
Una buena manera de determinar si una variable es predictiva consiste en entrenar un modelo de machine learning usando solamente esa variable. Luego, usamos el rendimiento del modelo para ranquear las variables y seleccionar las variables mejor ranqueadas.
## Librerias y funciones.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from feature_engine.selection import SelectBySingleFeaturePerformance
# Cargar dataset
breast_cancer = load_breast_cancer()
X = pd.DataFrame(breast_cancer.data, columns=breast_cancer.feature_names)
y = breast_cancer.target
# Separar dataset en conjunto de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# Seleccionar variables entrenando random forests de una variable
sel = SelectBySingleFeaturePerformance(
estimator=RandomForestClassifier(random_state=10),
scoring='roc_auc',
cv=3,
threshold=None,
)
# Seleccionar y eliminar variables en set de entrenamiento
X_train_t = sel.fit_transform(X_train, y_train)
# Eliminar variables en set de prueba
X_test_t = sel.transform(X_test)
En el código anterior, entrenamos random forests con cada una de las variables en el set de datos, y luego obtuvimos el ROC-AUC de cada modelo. Con este ROC-AUC ranqueamos las variables y elegimos aquellas variables que resultaron en modelos con ROC-AUC mayor que 0.5.
Hagamos un gráfico de barras para visualizar la importancia de las variables asignada por los modelos:
pd.Series(sel.feature_performance_).sort_values(
ascending=False).plot.bar(figsize=(8, 4))
plt.ylabel('roc-auc')
plt.title('ROC-AUC de modelos de una variable');
Correlación¶
Al entrenar modelos lineales como la regresión lineal o logística, la multicolinealidad puede afectar al rendimiento del modelo. Por lo tanto, puede ser útil eliminar las variables correlacionadas antes de entrenar dichos modelos.
Feature-engine tiene algoritmos que seleccionan variables basándose en su correlación. El SmartCorrelationSelector, en particular, encuentra grupos de variables correlacionadas y retiene aquella con menos datos faltantes, mayor cardinalidad o variabilidad, mayor correlacion con el target, o mayor importancia segun el modelo indicado.
Podemos encontrar variables correlacionadas utilizando el método pandas.corr.
## Librerias y funciones.
import pandas as pd
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier
from feature_engine.selection import SmartCorrelatedSelection
# Crear dataframe con variables correlacionadas
def make_data():
X, y = make_classification(n_samples=1000,
n_features=12,
n_redundant=4,
n_clusters_per_class=1,
weights=[0.50],
class_sep=2,
random_state=1)
# transform arrays into pandas df and series
colnames = ['var_'+str(i) for i in range(12)]
X = pd.DataFrame(X, columns=colnames)
return X, y
X, y = make_data()
# Identificar grupos de variables correlacionadas, y de cada grupo
# seleccionar la que tiene mayor importancia segun random forests
tr = SmartCorrelatedSelection(
variables=None,
method="pearson",
threshold=0.8,
missing_values="raise",
selection_method="model_performance",
estimator=DecisionTreeClassifier(random_state=1),
scoring='roc_auc',
cv=3,
)
# Encontrar variables correlacionadas y eliminarlas del set de datos
Xt = tr.fit_transform(X, y)
Xt
| var_0 | var_1 | var_2 | var_3 | var_5 | var_7 | var_10 | var_11 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1.471061 | -2.376400 | -0.247208 | 1.210290 | 0.091527 | -2.230170 | 2.070526 | -1.989335 |
| 1 | 1.819196 | 1.969326 | -0.126894 | 0.034598 | -0.186802 | -1.447490 | 1.184820 | -1.309524 |
| 2 | 1.625024 | 1.499174 | 0.334123 | -2.233844 | -0.313881 | -2.240741 | -0.066448 | -0.852703 |
| 3 | 1.939212 | 0.075341 | 1.627132 | 0.943132 | -0.468041 | -3.534861 | 0.713558 | 0.484649 |
| 4 | 1.579307 | 0.372213 | 0.338141 | 0.951526 | 0.729005 | -2.053965 | 0.398790 | -0.186530 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 995 | 1.803380 | -1.363868 | -0.048464 | -1.241394 | -0.136638 | 2.354715 | -0.144619 | 0.555170 |
| 996 | 2.073749 | 0.263967 | 1.269868 | 2.260748 | -0.959332 | 2.312738 | -0.182916 | 1.193456 |
| 997 | 2.442529 | 0.528868 | 0.230641 | -0.854581 | -1.066801 | 2.573196 | 0.021500 | -2.710394 |
| 998 | 1.451356 | -0.871014 | -0.117844 | -1.865016 | -0.276940 | -1.587082 | 0.340473 | 0.149377 |
| 999 | 1.721321 | -0.534328 | -0.331306 | -1.288487 | 0.364444 | -2.451474 | -0.416476 | -0.111816 |
1000 rows × 8 columns
Más sobre selección de variables¶
Si quieres aprender más sobre la selección de variables y cómo llevarla a cabo en Python, consulta mi curso y libro:
Puedes consultar también:
- Selección de variables con Scikit-learn
- Selección de variables con Feature-engine
- Selección de variables con MLXtend
- Selección de variables con Lasso
Información de sesión¶
import session_info
session_info.show(html=False)
----- feature_engine 1.8.3 matplotlib 3.10.1 numpy 2.1.3 pandas 2.2.3 session_info v1.0.1 sklearn 1.6.1 ----- IPython 9.1.0 jupyter_client 8.6.3 jupyter_core 5.7.2 notebook 6.5.7 ----- Python 3.12.9 | packaged by Anaconda, Inc. | (main, Feb 6 2025, 18:56:27) [GCC 11.2.0] Linux-6.11.0-29-generic-x86_64-with-glibc2.39 ----- Session information updated at 2025-07-21 10:00
Instrucciones para citar¶
¿Cómo citar este documento?
Si utilizas este documento o alguna parte de él, te agradecemos que lo cites. ¡Muchas gracias!
Selección de Variables en Machine Learning con Python por Soledad Galli, disponible bajo una licencia Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0 DEED) en https://www.cienciadedatos.net/documentos/py67-seleccion-variables-machine-learning-python.html
¿Te ha gustado el artículo? Tu ayuda es importante
Tu contribución me ayudará a seguir generando contenido divulgativo gratuito. ¡Muchísimas gracias! 😊
Este documento creado por Soledad Galli tiene licencia Attribution-NonCommercial-ShareAlike 4.0 International.
Se permite:
-
Compartir: copiar y redistribuir el material en cualquier medio o formato.
-
Adaptar: remezclar, transformar y crear a partir del material.
Bajo los siguientes términos:
-
Atribución: Debes otorgar el crédito adecuado, proporcionar un enlace a la licencia e indicar si se realizaron cambios. Puedes hacerlo de cualquier manera razonable, pero no de una forma que sugiera que el licenciante te respalda o respalda tu uso.
-
No-Comercial: No puedes utilizar el material para fines comerciales.
-
Compartir-Igual: Si remezclas, transformas o creas a partir del material, debes distribuir tus contribuciones bajo la misma licencia que el original.

