Más sobre ciencia de datos: cienciadedatos.net
- Regresión lineal con Python
- Regresión lineal múltiple con Python
- Regresión logística con Python
- Regularización Ridge, Lasso y Elastic Net con Python
- Machine learning con Python y Scikitlearn
- Árboles de decisión con Python: regresión y clasificación
- Random Forest con Python y Scikit-learn
- Gradient Boosting con Python y Scikit-learn
- Gradient Boosting probabilístico con Python
- Máquinas de Vector Soporte (SVM)
- Redes neuronales con Python
- Análisis de componentes principales PCA
- Clustering
- Detección de anomalías con PCA
- Detección de anomalías con autoencoders
- Detección de anomalías con Gaussian Mixture Models
- Detección de anomalías con Isolation Forest
- Análisis de texto (text mining) con Python
- Reglas de asociación
- Análisis Tweets con Python

Introducción¶
La regresión lineal es un método estadístico que trata de modelar la relación entre una variable continua y una o más variables independientes mediante el ajuste de una ecuación lineal. Se llama regresión lineal simple cuando solo hay una variable independiente y regresión lineal múltiple cuando hay más de una. Dependiendo del contexto, a la variable modelada se le conoce como variable dependiente o variable respuesta, y a las variables independientes como regresores, predictores o features.
A lo largo de este documento, se describen de forma progresiva los fundamentos teóricos de la regresión lineal, los principales aspectos prácticos a tener en cuenta y ejemplos de cómo crear este tipo de modelos en Python.
Modelos de regresión lineal en Python
Dos de las implementaciones de modelos de regresión lineal más utilizadas en Python son: scikit-learn y statsmodels. Aunque ambas están muy optimizadas, Scikit-learn está orientada principalmente a la predicción, por lo que no dispone de apenas funcionalidades que muestren las muchas características del modelo que se deben analizar para hacer inferencia. Statsmodels es mucho más completo en este sentido.
Definición matemática¶
El modelo de regresión lineal (Legendre, Gauss, Galton y Pearson) considera que, dado un conjunto de observaciones $\{y_i, x_{i1},...,x_{np}\}^{n}_{i=1}$, la media $\mu$ de la variable respuesta $y$ se relaciona de forma lineal con la o las variables regresoras $x_1$ ... $x_p$ acorde a la ecuación:
$$\mu_y = \beta_0 + \beta_1 x_{1} + \beta_2 x_{2} + ... + \beta_p x_{p}$$El resultado de esta ecuación se conoce como la línea de regresión poblacional, y recoge la relación entre los predictores y la media de la variable respuesta.
Otra definición que se encuentra con frecuencia en los libros de estadística es:
$$y_i= \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + ... + \beta_p x_{ip} +\epsilon_i$$En este caso, se está haciendo referencia al valor de $y$ para una observación $i$ concreta. El valor de una observación puntual nunca va a ser exactamente igual al promedio, de ahí que se añada el término de error $\epsilon$.
En ambos casos, la interpretación de los elementos del modelo es la misma:
$\beta_{0}$: es la ordenada en el origen, se corresponde con el valor promedio de la variable respuesta $y$ cuando todos los predictores son cero.
$\beta_{j}$: es el efecto promedio que tiene sobre la variable respuesta el incremento en una unidad de la variable predictora $x_{j}$, manteniéndose constantes el resto de variables. Se conocen como coeficientes parciales de regresión.
$e$: es el residuo o error, la diferencia entre el valor observado y el estimado por el modelo. Recoge el efecto de todas aquellas variables que influyen en $y$ pero que no se incluyen en el modelo como predictores.
En la gran mayoría de casos, los valores $\beta_0$ y $\beta_j$ poblacionales se desconocen, por lo que, a partir de una muestra, se obtienen sus estimaciones $\hat{\beta}_0$ y $\hat{\beta}_j$. Ajustar el modelo consiste en estimar, a partir de los datos disponibles, los valores de los coeficientes de regresión que maximizan la verosimilitud (likelihood), es decir, los que dan lugar al modelo que con mayor probabilidad puede haber generado los datos observados.
El método empleado con más frecuencia es el ajuste por mínimos cuadrados ordinarios (OLS), que identifica como mejor modelo la recta (o plano si es regresión múltiple) que minimiza la suma de las desviaciones verticales entre cada dato de entrenamiento y la recta, elevadas al cuadrado.
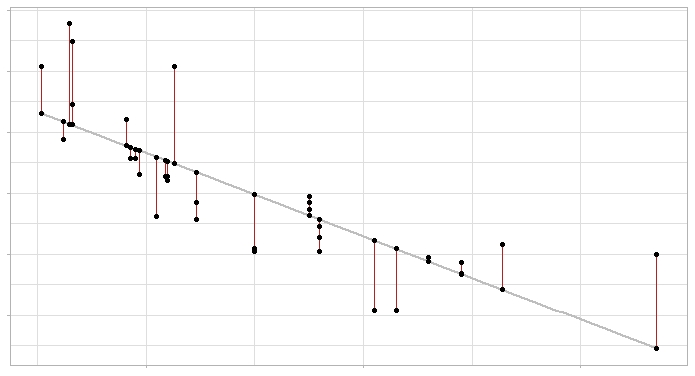
Modelo de regresión lineal y sus errores: la línea gris representa la recta de regresión (el modelo) y los segmentos rojos el error entre esta y cada observación.
Computacionalmente, estos cálculos son más eficientes si se realizan de forma matricial:
$$\mathbf{y}=\mathbf{X}^T \mathbf{\beta}+\epsilon$$Una vez estimados los coeficientes, se pueden obtener las estimaciones de cada observación ($\hat{y}_i$):
$$\hat{y}_i= \hat{\beta}_0 + \hat{\beta}_1 x_{i1} + \hat{\beta}_2 x_{i2} + ... + \hat{\beta}_p x_{ip}$$Finalmente, la estimación de la varianza del modelo ($\hat{\sigma}^2$) se obtiene como:
$$\hat{\sigma}^2 = \frac{\sum^n_{i=1} \hat{\epsilon}_i^2}{n-p} = \frac{\sum^n_{i=1} (y_i - \hat{y}_i)^2}{n-p}$$donde $n$ es el número de observaciones y $p$ el número de predictores.
Interpretación del modelo¶
Los principales elementos que hay que interpretar en un modelo de regresión lineal son los coeficientes de los predictores:
$\beta_{0}$ es la ordenada en el origen o intercept, se corresponde con el valor esperado de la variable respuesta $y$ cuando todos los predictores son cero.
$\beta_{j}$ los coeficientes de regresión parcial de cada predictor indican el cambio promedio esperado de la variable respuesta $y$ al incrementar en una unidad de la variable predictora $x_{j}$, manteniéndose constantes el resto de variables.
La magnitud de cada coeficiente parcial de regresión depende de las unidades en las que se mida la variable predictora a la que corresponde, por lo que su magnitud no está asociada con la importancia de cada predictor.
Para poder determinar qué impacto tienen en el modelo cada una de las variables, se emplean los coeficientes parciales estandarizados, que se obtienen al estandarizar (sustraer la media y dividir entre la desviación estándar) las variables predictoras previo ajuste del modelo. En este caso, $\beta_{0}$ se corresponde con el valor esperado de la variable respuesta cuando todos los predictores se encuentran en su valor promedio, y $\beta_{j}$ el cambio promedio esperado de la variable respuesta al incrementar en una desviación estándar la variable predictora $x_{j}$, manteniéndose constantes el resto de variables.
Si bien los coeficientes de regresión suelen ser el primer objetivo de la interpretación de un modelo lineal, existen muchos otros aspectos (significancia del modelo en su conjunto, significancia de los predictores, condición de normalidad...). Estos últimos suelen ser tratados con poca detalle cuando el único objetivo del modelo es realizar predicciones, sin embargo, son muy relevantes si se quiere realizar inferencia, es decir, explicar las relaciones entre los predictores y la variable respuesta. A lo largo de este documento se irán introduciendo cada uno de ellos.
Significado "lineal"
El término "lineal" en los modelos de regresión hace referencia al hecho de que los parámetros se incorporan en la ecuación de forma lineal, no a que necesariamente la relación entre cada predictor y la variable respuesta tenga que seguir un patrón lineal.
La siguiente ecuación muestra un modelo lineal en el que el predictor $x_1$ no es lineal respecto a y:
$$y = \beta_0 + \beta_1x_1 + \beta_2log(x_1) + \epsilon$$import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
x1 = np.linspace(1,5, num=100)
x2 = np.linspace(1,5, num=100)
y = 0.0 + 0.5*x1 - 0.8*np.log(x2)
fig, ax = plt.subplots(figsize=(5, 2.5))
ax.plot(x1, y)
ax.set_xlabel("x1")
ax.set_ylabel("y");
En contraposición, el siguiente no es un modelo lineal:
$$y = \beta_0 + \beta_1x_1^{\beta_2} + \epsilon$$En ocasiones, algunas relaciones no lineales pueden transformarse de forma que se pueden expresar de manera lineal:
$$y = \beta_0x_1^{\beta_1}\epsilon $$ $$log(y)=log(\beta_0) + \beta_1log(x_1) + log(\epsilon)$$Bondad de ajuste del modelo¶
Una vez ajustado el modelo, es necesario verificar su utilidad ya que, aun siendo la línea que mejor se ajusta a las observaciones de entre todas las posibles, puede tener un gran error. Las métricas más utilizadas para medir la calidad del ajuste son: el error estándar de los residuos y el coeficiente de determinación $R^2$.
Error estándar de los residuos (Residual Standar Error, RSE)
Mide la desviación promedio de cualquier punto estimado por el modelo respecto de la recta de regresión. Tiene las mismas unidades que la variable respuesta. Una forma de saber si el valor del RSE es elevado consiste en dividirlo entre el valor medio de la variable respuesta, obteniendo así un % de la desviación.
$$RSE = \sqrt{\frac{1}{n-p-1}RSS}$$En modelos lineales simples, dado que hay un único predictor $(n-p-1) = (n-2)$.
Coeficiente de determinación $R^2$
$R^2$ describe la proporción de varianza de la variable respuesta explicada por el modelo y relativa a la varianza total. Su valor está acotado entre 0 y 1. Al ser adimensional, presenta la ventaja frente al RSE de ser más fácil de interpretar.
$$R^{2}=\frac{\text{Suma de cuadrados totales - Suma de cuadrados residuales}}{\text{Suma de cuadrados totales}}=$$$$1-\frac{\text{Suma de cuadrados residuales}}{\text{Suma de cuadrados totales}} = $$ $$1-\frac{\sum(\hat{y_i}-y_i)^2}{\sum(y_i-\overline{y})^2}$$En los modelos de regresión lineal simple el valor de $R^2$ se corresponde con el cuadrado del coeficiente de correlación de Pearson (r) entre $x$ e $y$, no siendo así en regresión múltiple.
En los modelos lineales múltiples, cuantos más predictores se incluyan en el modelo, mayor es el valor de $R^2$. Esto es así ya que, por poco que sea, cada predictor va a explicar una parte de la variabilidad observada en $y$. Es por esto que $R^2$ no puede utilizarse para comparar modelos con distinto número de predictores.
$R^2_{ajustado}$ introduce una penalización al valor de $R^2$ por cada predictor que se añade al modelo. El valor de la penalización depende del número de predictores utilizados y del tamaño de la muestra, es decir, del número de grados de libertad. Cuanto mayor es el tamaño de la muestra, más predictores se pueden incorporar en el modelo. $R^2_{ajustado}$ permite encontrar el mejor modelo, aquel que consigue explicar mejor la variabilidad de $y$ con el menor número de predictores.
$$R^{2}_{ajustado} = 1 - \frac{SSE}{SST}x\frac{n-1}{n-p-1} = R^{2} - (1-R^{2})\frac{n-1}{n-p-1} = 1-\frac{SSE/df_{e}}{SST/df_{t}}$$siendo $SSE$ la variabilidad explicada por el modelo (Sum of Squares Explained), $SST$ la variabilidad total de $y$ (Sum of Squares Total), $n$ el tamaño de la muestra y $p$ el número de predictores introducidos en el modelo.
Significancia del modelo F-test¶
Uno de los primeros resultados que hay que evaluar al ajustar un modelo es el resultado del test de significancia $F$. Este contraste responde a la pregunta de si el modelo en su conjunto es capaz de predecir la variable respuesta mejor de lo esperado por azar, o lo que es equivalente, si al menos uno de los predictores que forman el modelo contribuye de forma significativa. Para realizar este contraste se compara la suma de residuos cuadrados del modelo de interés con la del modelo sin predictores, formado únicamente por la media (también conocido como suma de cuadrados corregidos por la media, $TSS$).
$$F = \frac{(TSS - RSS)/(p-1)}{RSS/(n-p)}$$Con frecuencia, la hipótesis nula y alternativa de este test se describen como:
$H_0$: $\beta_1$ = ... = $\beta_{p-1} = 0$
$H_a$: al menos un $\beta_i \neq 0$
Si el test $F$ resulta significativo, implica que el modelo es útil, pero no que sea el mejor. Podría ocurrir que alguno de sus predictores no fuese necesario.
Significancia de los predictores¶
En la mayoría de casos, aunque el estudio de regresión se aplica a una muestra, el objetivo último es obtener un modelo lineal que explique la relación entre las variables en toda la población. Esto significa que, el modelo generado, es una estimación de la relación poblacional a partir de la relación que se observa en la muestra y, por lo tanto, está sujeta a variaciones. Para cada uno de los coeficientes de la ecuación de regresión lineal ($\beta_j$) se puede calcular su significancia (p-value) y su intervalo de confianza. El test estadístico más empleado es el t-test (existen alternativas no paramétricas).
El test de significancia para los coeficientes ($\beta_j$) del modelo lineal considera como hipótesis:
$H_0$: el predictor $x_j$ no contribuye al modelo ($\beta_j = 0$), en presencia del resto de predictores. En el caso de regresión lineal simple, se puede interpretar también como que no existe relación lineal entre ambas variables por lo que la pendiente del modelo es cero $\beta_j = 0$.
$H_a$: el predictor $x_j$ sí contribuye al modelo ($\beta_j \neq 0$), en presencia del resto de predictores. En el caso de regresión lineal simple, se puede interpretar también como que sí existe relación lineal entre ambas variables por lo que la pendiente del modelo es distinta de cero $\beta_j \neq 0$.
Cálculo del estadístico T y del p-value:
donde
$$SE(\hat{\beta}_j)^2 = \frac{\sigma^2}{\sum^n_{i=1}(x_{ji} -\overline{x})^2}$$La varianza del error $\sigma^2$ se estima a partir del Residual Standar Error (RSE), que puede entenderse como la diferencia promedio que se desvía la variable respuesta de la verdadera línea de regresión. En el caso de regresión lineal simple, RSE equivale a:
$$RSE = \sqrt{\frac{1}{n-2}RSS} = \sqrt{\frac{1}{n-2}\sum^n_{i=1}(y_i -\hat{y}_i)}$$Grados de libertad (df) = número observaciones - 2 = número observaciones -número predictores - 1
p-value = P(|t| > valor calculado de t)
Intervalos de confianza
Cuanto menor es el número de observaciones $n$, menor la capacidad para calcular el error estándar del modelo. Como consecuencia, la exactitud de los coeficientes de regresión estimados se reduce. Esto tiene importancia sobretodo en la regresión múltiple.
En los modelos generados con statsmodels se devuelve, junto con el valor de los coeficientes de regresión, el valor del estadístico $t$ obtenido para cada uno, los p-value y los intervalos de confianza correspondientes. Esto permite saber, además de las estimaciones, si son significativamente distintos de 0, es decir, si contribuyen al modelo.
Para que los cálculos descritos anteriormente sean válidos, se tiene que asumir que los residuos son independientes y que se distribuyen de forma normal con media 0 y varianza $\sigma^2$. Cuando la condición de normalidad no se satisface, existe la posibilidad de recurrir a los test de permutación para calcular significancia (p-value) y al bootstrapping para calcular intervalos de confianza.
Variables categóricas como predictores¶
Cuando se introduce una variable categórica como predictor, un nivel se considera el de referencia (normalmente codificado como 0) y el resto de niveles se comparan con él. En el caso de que el predictor categórico tenga más de dos niveles, se generan lo que se conoce como variables dummy o one-hot-encodding, que son variables creadas para cada uno de los niveles del predictor categórico y que pueden tomar el valor de 0 o 1. Cada vez que se emplee el modelo para predecir un valor, solo una variable dummy por predictor adquiere el valor 1 (la que coincida con el valor que adquiere el predictor en ese caso) mientras que el resto se consideran 0. El valor del coeficiente parcial de regresión $\beta_j$ de cada variable dummy indica el porcentaje promedio en el que influye dicho nivel sobre la variable dependiente $y$ en comparación con el nivel de referencia de dicho predictor.
La idea de variables dummy se entiende mejor con un ejemplo. Supóngase un modelo en el que la variable respuesta peso se predice en función de la altura y nacionalidad del sujeto. La variable nacionalidad es cualitativa con 3 niveles (americana, europea y asiática). A pesar de que el predictor inicial es nacionalidad, se crea una variable nueva por cada nivel, cuyo valor puede ser 0 o 1. De tal forma que la ecuación del modelo completo es:
$$peso = \beta_0 + \beta_1altura + \beta_2americana + \beta_3europea + \beta_4asiatica$$Si el sujeto es europeo, las variables dummy americana y asiática se consideran 0, de forma que el modelo para este caso se queda en:
$$peso = \beta_0 + \beta_1altura + \beta_3europea$$Predicción¶
Una vez generado un modelo válido, es posible predecir el valor de la variable respuesta $y$ para nuevos valores de las variables predictoras $x$. Es importante tener en cuenta que las predicciones deben, a priori, limitarse al rango de valores dentro del que se encuentran las observaciones con las que se ha entrenado el modelo. Esto es importante puesto que, aunque los modelos lineales pueden extrapolarse, solo en esta región se tiene certeza de que se cumplen las condiciones para que el modelo sea válido. Para calcular las predicciones, se emplea la ecuación generada por regresión.
$$\hat{y}_i= \hat{\beta}_0 + \hat{\beta}_1 x_{i1} + \hat{\beta}_2 x_{i2} + ... + \hat{\beta}_p x_{ip}$$Dado que el modelo se ha obtenido a partir de una muestra, las estimaciones de los coeficientes de regresión tienen un error asociado y, por lo tanto, también lo tienen los valores de las predicciones generadas con ellos. Existen dos formas de medir la incertidumbre asociada con una predicción:
- Intervalos de confianza: intervalo del valor promedio esperado de la variable respuesta $y$ para un determinado valor $x$.
- Intervalos de predicción: intervalo del valor esperado de la variable respuesta $y$ para un determinado valor $x$.
Si bien ambos parecen similares, la diferencia se encuentra en que los intervalos de confianza se aplican al valor promedio que se espera de $y$ para un determinado valor de $x$, mientras que los intervalos de predicción no se aplican al promedio. Por esta razón, los segundos siempre son más amplios que los primeros.
Una característica que deriva de la forma en que se calcula el margen de error en los intervalos de confianza y predicción, es que el intervalo se ensancha a medida que los valores de $x$ se aproximan a los extremos del rango observado.
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
bateos = [5659, 5710, 5563, 5672, 5532, 5600, 5518, 5447, 5544, 5598,
5585, 5436, 5549, 5612, 5513, 5579, 5502, 5509, 5421, 5559,
5487, 5508, 5421, 5452, 5436, 5528, 5441, 5486, 5417, 5421]
runs = [855, 875, 787, 730, 762, 718, 867, 721, 735, 615, 708, 644, 654, 735,
667, 713, 654, 704, 731, 743, 619, 625, 610, 645, 707, 641, 624, 570,
593, 556]
datos = pd.DataFrame({'bateos': bateos, 'runs': runs})
fig, ax = plt.subplots(figsize=(5, 2.5))
sns.regplot(x='runs', y='bateos', data=datos, ax = ax);
¿Por qué ocurre esto? Prestando atención a la ecuación del error estándar del intervalo de confianza, el numerador contiene el término $(x_k - \bar{x})^2$ (lo mismo ocurre para el intervalo de predicción).
$$\sqrt{MSE \left(\frac{1}{n} + \frac{(x_k - \bar{x})^2}{\sum^n_{i=1}(x_i - \bar{x}^2)} \right)}$$Este término se corresponde con la diferencia al cuadrado entre el valor $x_k$ para el que se hace la predicción y la media $\bar{x}$ de los valores observados del predictor $x$. Cuanto más se aleje $x_k$ de $\bar{x}$ mayor es el numerador y por lo tanto el error estándar.
Validación del modelo¶
Una vez seleccionado el mejor modelo que se puede crear con los datos disponibles, se tiene que comprobar su capacidad prediciendo nuevas observaciones que no se hayan empleado para entrenarlo, de este modo se verifica si el modelo se puede generalizar. Una estrategia comúnmente empleada es dividir aleatoriamente los datos en dos grupos, ajustar el modelo con el primer grupo y estimar la precisión de las predicciones con el segundo.
El tamaño adecuado de las particiones depende en gran medida de la cantidad de datos disponibles y la seguridad que se necesite en la estimación del error, 80%-20% suele dar buenos resultados.
Condiciones para la regresión lineal¶
Para que un modelo de regresión lineal por mínimos cuadrados, y las conclusiones derivadas de él, sean completamente válidas, se deben verificar que se cumplen las asunciones sobre las que se basa su desarrollo matemático. En la práctica, rara vez se cumplen, o se puede demostrar que se cumplen todas, sin embargo esto no significa que el modelo no sea útil. Lo importante es ser consciente de ellas y del impacto que esto tiene en las conclusiones que se extraen del modelo.
No colinealidad o multicolinealidad:
En los modelos lineales múltiples, los predictores deben ser independientes, no debe de haber colinealidad entre ellos. La colinealidad ocurre cuando un predictor está linealmente relacionado con uno o varios de los otros predictores del modelo. Como consecuencia de la colinealidad, no se puede identificar de forma precisa el efecto individual que tiene cada predictor sobre la variable respuesta, lo que se traduce en un incremento de la varianza de los coeficientes de regresión estimados hasta el punto de que resulta imposible establecer su significancia estadística. Además, pequeños cambios en los datos, provocan grandes cambios en las estimaciones de los coeficientes. Si bien la colinealidad propiamente dicha existe solo si el coeficiente de correlación simple o múltiple entre predictores es 1, cosa que raramente ocurre en la realidad, es frecuente encontrar la llamada casi-colinealidad o multicolinealidad no perfecta.
No existe un método estadístico concreto para determinar la existencia de colinealidad o multicolinealidad entre los predictores de un modelo de regresión, sin embargo, se han desarrollado numerosas reglas prácticas que tratan de determinar en qué medida afectan al modelo. Los pasos recomendados a seguir son:
Si el coeficiente de determinación $R^2$ es alto pero ninguno de los predictores resulta significativo, hay indicios de colinealidad.
Crear una matriz de correlación en la que se calcula la relación lineal entre cada par de predictores. Es importante tener en cuenta que, a pesar de no obtenerse ningún coeficiente de correlación alto, no está asegurado que no exista multicolinealidad. Se puede dar el caso de tener una relación lineal casi perfecta entre tres o más variables y que las correlaciones simples entre pares de estas mismas variables no sean mayores que 0.5.
Generar un modelo de regresión lineal simple entre cada uno de los predictores frente al resto. Si en alguno de los modelos el *coeficiente de determinación $R^2$ es alto, estaría señalando a una posible colinealidad.
Tolerancia (TOL) y Factor de Inflación de la Varianza (VIF). Se trata de dos parámetros que vienen a cuantificar lo mismo (uno es el inverso del otro). El VIF de cada predictor se calcula según la siguiente fórmula:
Donde $R^2$ se obtiene de la regresión del predictor $X_j$ sobre los otros predictores. Esta es la opción más recomendada, los límites de referencia que se suelen emplear son:
VIF = 1: ausencia total de colinealidad
1 < VIF < 5: la regresión puede verse afectada por cierta colinealidad.
5 < VIF < 10: la regresión puede verse altamente afectada por cierta colinealidad.
El término tolerancia es $\frac{1}{VIF}$ por lo que los límites recomendables están entre 1 y 0.1.
En caso de encontrar colinealidad entre predictores, hay dos posibles soluciones. La primera es excluir uno de los predictores problemáticos intentando conservar el que, a juicio del investigador, está influyendo realmente en la variable respuesta. Esta medida no suele tener mucho impacto en el modelo en cuanto a su capacidad predictiva ya que, al existir colinealidad, la información que aporta uno de los predictores es redundante en presencia del otro. La segunda opción consiste en combinar las variables colineales en un único predictor, aunque con el riesgo de perder su interpretación.
Cuando se intenta establecer relaciones causa-efecto, la colinealidad puede llevar a conclusiones muy erróneas, haciendo creer que una variable es la causa cuando, en realidad, es otra la que está influenciando sobre ese predictor.
Relación lineal entre los predictores numéricos y la variable respuesta
Cada predictor numérico tiene que estar linealmente relacionado con la variable respuesta $y$ mientras los demás predictores se mantienen constantes, de lo contrario no se deben introducir en el modelo. La forma más recomendable de comprobarlo es representando los residuos del modelo frente a cada uno de los predictores. Si la relación es lineal, los residuos se distribuyen de forma aleatoria en torno a cero. Estos análisis son solo aproximados, ya que no hay forma de saber si realmente la relación es lineal cuando el resto de predictores se mantienen constantes.
Distribución normal de la variable respuesta
La variable respuesta se tiene que distribuir de forma normal. Para comprobarlo se recurre a histogramas, a los cuantiles normales o a test de hipótesis de normalidad.
Varianza constante de la variable respuesta (homocedasticidad)
La varianza de la variable respuesta debe ser constante en todo el rango de los predictores. Para comprobarlo suelen representarse los residuos del modelo frente a cada predictor. Si la varianza es constante, se distribuyen de forma aleatoria manteniendo una misma dispersión y sin ningún patrón específico. Una distribución cónica es un claro identificador de falta de homocedasticidad. También se puede recurrir a contrastes de homocedasticidad como el test de Breusch-Pagan.
La razón de esta condición reside en los siguiente: los modelos lineales asumen que la variable respuesta $y$ sigue una distribución normal, cuya media $\mu$ puede ser modelada en función de otras variables (predictores) y cuya varianza $\sigma$ se calcula mediante una constante de dispersión y una función $\nu(\mu)$. Esto último significa que, la varianza, no se modelan directamente en función de las variables predictoras sino de forma indirecta a través de su relación con la media y es un valor único.
$$\hat{\sigma}^2 = \frac{\sum^n_{i=1} \hat{\epsilon}_i^2}{n-p} = \frac{\sum^n_{i=1} (y_i - \hat{\mu})^2}{n-p}$$¿Qué impacto puede tener esto en la práctica? Si bien las estimación de la media obtenidas por estos modelos son buenas, no lo son tanto las incertidumbres asociadas y, en consecuencia, los intervalos de confianza y de predicción que se puedan calcular.
No autocorrelación (Independencia)
Los valores de cada observación son independientes de los otros. Esto es especialmente importante de comprobar cuando se trabaja con mediciones temporales. Se recomienda representar los residuos ordenados acorde al tiempo de registro de las observaciones, si existe un cierto patrón hay indicios de autocorrelación. También se puede emplear el test de hipótesis de Durbin-Watson.
Valores atípicos, con alto leverage o influyentes
Es importante identificar observaciones que sean atípicas o que puedan estar influenciando al modelo. La forma más fácil de detectarlas es a través de los residuos (ver más detalles adelante).
Tamaño de la muestra
No se trata de una condición de por sí pero, si no se dispone de suficientes observaciones, predictores que no son realmente influyentes podrían parecerlo. Un recomendación frecuente es que el número de observaciones sea como mínimo entre 10 y 20 veces el número de predictores del modelo.
Parsimonia
Este término hace referencia a que, el mejor modelo, es aquel capaz de explicar con mayor precisión la variabilidad observada en la variable respuesta empleando el menor número de predictores, por lo tanto, con menos asunciones.
La gran mayoría de condiciones se verifican utilizando los residuos, por lo tanto, se suele generar primero el modelo y posteriormente validar las condiciones. De hecho, el ajuste de un modelo debe verse como un proceso iterativo en el que se ajusta el modelo, se evalúan sus residuos y se mejora. Así hasta llegar a un modelo óptimo.
Valores atípicos (outliers)¶
Independientemente de que el modelo se haya podido aceptar, siempre es conveniente identificar si hay algún posible outlier, observación con alto leverage o influyente, puesto que podría estar condicionando en gran medida el modelo. La eliminación de este tipo de observaciones debe de analizarse con detalle y dependiendo de la finalidad del modelo. Si el fin es predictivo, un modelo sin outliers ni observaciones altamente influyentes suele ser capaz de predecir mejor la mayoría de casos. Sin embargo, es muy importante prestar atención a estos valores ya que, de no tratarse de errores de medida, pueden ser los casos más interesantes. El modo adecuado de proceder cuando se sospecha de algún posible valor atípico o influyente es calcular el modelo de regresión incluyendo y excluyendo dicho valor.
Ejemplo regresión lineal simple¶
Supóngase que un analista de deportes quiere saber si existe una relación entre el número de veces que batean los jugadores de un equipo de béisbol y el número de runs que consigue. En caso de existir y de establecer un modelo, podría predecir el resultado del partido
Librerías¶
Las librerías utilizadas en este ejemplo son:
# Tratamiento de datos
# ==============================================================================
import pandas as pd
# Gráficos
# ==============================================================================
import matplotlib.pyplot as plt
# Preprocesado y modelado
# ==============================================================================
from scipy.stats import pearsonr
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error
import statsmodels.api as sm
# Configuración matplotlib
# ==============================================================================
plt.style.use('fivethirtyeight')
plt.rcParams.update({'font.size': 10, 'lines.linewidth': 1.5})
# Configuración warnings
# ==============================================================================
import warnings
warnings.filterwarnings('once')
Datos¶
# Datos
# ==============================================================================
equipos = ["Texas","Boston","Detroit","Kansas","St.","New_S.","New_Y.",
"Milwaukee","Colorado","Houston","Baltimore","Los_An.","Chicago",
"Cincinnati","Los_P.","Philadelphia","Chicago","Cleveland","Arizona",
"Toronto","Minnesota","Florida","Pittsburgh","Oakland","Tampa",
"Atlanta","Washington","San.F","San.I","Seattle"]
bateos = [5659, 5710, 5563, 5672, 5532, 5600, 5518, 5447, 5544, 5598,
5585, 5436, 5549, 5612, 5513, 5579, 5502, 5509, 5421, 5559,
5487, 5508, 5421, 5452, 5436, 5528, 5441, 5486, 5417, 5421]
runs = [855, 875, 787, 730, 762, 718, 867, 721, 735, 615, 708, 644, 654, 735,
667, 713, 654, 704, 731, 743, 619, 625, 610, 645, 707, 641, 624, 570,
593, 556]
datos = pd.DataFrame({'equipos': equipos, 'bateos': bateos, 'runs': runs})
datos.head(3)
| equipos | bateos | runs | |
|---|---|---|---|
| 0 | Texas | 5659 | 855 |
| 1 | Boston | 5710 | 875 |
| 2 | Detroit | 5563 | 787 |
Representación gráfica¶
El primer paso antes de generar un modelo de regresión simple es representar los datos para poder intuir si existe una relación y cuantificar dicha relación mediante un coeficiente de correlación.
# Gráfico
# ==============================================================================
fig, ax = plt.subplots(figsize=(6, 3.84))
datos.plot(
x = 'bateos',
y = 'runs',
c = 'firebrick',
kind = "scatter",
ax = ax
)
ax.set_title('Distribución de bateos y runs');
# Correlación lineal entre las dos variables
# ==============================================================================
corr_test = pearsonr(x = datos['bateos'], y = datos['runs'])
print(f"Coeficiente de correlación de Pearson: {corr_test[0]}")
print(f"P-value: {corr_test[1]}")
Coeficiente de correlación de Pearson: 0.6106270467206688 P-value: 0.00033883513597919785
El gráfico y el test de correlación muestran una relación lineal, de intensidad considerable (r = 0.61) y significativa (p-value = 0.000339). Tiene sentido intentar generar un modelo de regresión lineal con el objetivo de predecir el número de runs en función del número de bateos del equipo.
Ajuste del modelo¶
Se ajusta un modelo empleando como variable respuesta runs y como predictor bateos. Como en todo estudio predictivo, no solo es importante ajustar el modelo, sino también cuantificar su capacidad para predecir nuevas observaciones. Para poder hacer esta evaluación, se dividen los datos en dos grupos, uno de entrenamiento y otro de test.
Scikit-learn¶
# División de los datos en train y test
# ==============================================================================
X = datos[['bateos']]
y = datos['runs']
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
train_size = 0.8,
random_state = 1234,
shuffle = True
)
# Creación del modelo
# ==============================================================================
modelo = LinearRegression()
modelo.fit(X = X_train, y = y_train)
LinearRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression()
# Información del modelo
# ==============================================================================
print(f"Intercept: {modelo.intercept_}")
print(f"Coeficiente: {list(zip(modelo.feature_names_in_, modelo.coef_))}")
print(f"Coeficiente de determinación R^2:", modelo.score(X, y))
Intercept: -2367.702841302211
Coeficiente: [('bateos', 0.5528713534479736)]
Coeficiente de determinación R^2: 0.3586119899498744
Una vez entrenado el modelo, se evalúa la capacidad predictiva empleando el conjunto de test.
# Error de test del modelo
# ==============================================================================
predicciones = modelo.predict(X=X_test)
rmse = root_mean_squared_error(y_true=y_test, y_pred=predicciones)
print(f"Primeras cinco predicciones: {predicciones[0:5]}")
print(f"El error (rmse) de test es: {rmse}")
Primeras cinco predicciones: [643.78742093 720.0836677 690.78148597 789.19258689 627.20128033] El error (rmse) de test es: 59.336716083360486
Statsmodels¶
La implementación de regresión lineal de Statsmodels, es más completa que la de Scikitlearn ya que, además de ajustar el modelo, permite calcular los test estadísticos y análisis necesarios para verificar que se cumplen las condiciones sobre las que se basa este tipo de modelos. Statsmodels tiene dos formas de entrenar el modelo:
Indicando la fórmula del modelo y pasando los datos de entrenamiento como un dataframe que incluye la variable respuesta y los predictores. Esta forma es similar a la utilizada en R.
Pasar dos matrices, una con los predictores y otra con la variable respuesta. Esta es igual a la empleada por Scikitlearn con la diferencia de que a la matriz de predictores hay que añadirle una primera columna de 1s.
# División de los datos en train y test
# ==============================================================================
X = datos[['bateos']]
y = datos['runs']
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
train_size = 0.8,
random_state = 1234,
shuffle = True
)
# Creación del modelo utilizando matrices como en scikit-learn
# ==============================================================================
# A la matriz de predictores se le añade una columna de 1s para el intercept del modelo
X_train = sm.add_constant(X_train, prepend=True)
modelo = sm.OLS(endog=y_train, exog=X_train)
modelo = modelo.fit()
print(modelo.summary())
OLS Regression Results
==============================================================================
Dep. Variable: runs R-squared: 0.271
Model: OLS Adj. R-squared: 0.238
Method: Least Squares F-statistic: 8.191
Date: Thu, 13 Feb 2025 Prob (F-statistic): 0.00906
Time: 18:04:39 Log-Likelihood: -134.71
No. Observations: 24 AIC: 273.4
Df Residuals: 22 BIC: 275.8
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -2367.7028 1066.357 -2.220 0.037 -4579.192 -156.214
bateos 0.5529 0.193 2.862 0.009 0.152 0.953
==============================================================================
Omnibus: 5.033 Durbin-Watson: 1.902
Prob(Omnibus): 0.081 Jarque-Bera (JB): 3.170
Skew: 0.829 Prob(JB): 0.205
Kurtosis: 3.650 Cond. No. 4.17e+05
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 4.17e+05. This might indicate that there are
strong multicollinearity or other numerical problems.
Intervalos de confianza de los coeficientes¶
# Intervalos de confianza para los coeficientes del modelo
# ==============================================================================
intervalos_ci = modelo.conf_int(alpha=0.05)
intervalos_ci.columns = ['2.5%', '97.5%']
intervalos_ci
| 2.5% | 97.5% | |
|---|---|---|
| const | -4579.192050 | -156.213633 |
| bateos | 0.152244 | 0.953499 |
Predicciones¶
Una vez entrenado el modelo, se pueden obtener predicciones para nuevos datos. Los modelos de statsmodels permiten calcular las predicciones de dos formas:
.predict(): devuelve únicamente el valor de las predicciones..get_prediction().summary_frame(): devuelve, además de las predicciones, los intervalos de confianza asociados.
# Predicciones con intervalo de confianza del 95%
# ==============================================================================
predicciones = modelo.get_prediction(exog=X_train).summary_frame(alpha=0.05)
predicciones.head(4)
| mean | mean_se | mean_ci_lower | mean_ci_upper | obs_ci_lower | obs_ci_upper | |
|---|---|---|---|---|---|---|
| 3 | 768.183475 | 32.658268 | 700.454374 | 835.912577 | 609.456054 | 926.910897 |
| 23 | 646.551778 | 19.237651 | 606.655332 | 686.448224 | 497.558860 | 795.544695 |
| 14 | 680.276930 | 14.186441 | 650.856053 | 709.697807 | 533.741095 | 826.812765 |
| 13 | 735.011194 | 22.767596 | 687.794091 | 782.228298 | 583.893300 | 886.129088 |
Representación gráfica del modelo¶
Además de la línea de mínimos cuadrados, es recomendable incluir los límites superior e inferior del intervalo de confianza. Esto permite identificar la región en la que, según el modelo generado y para un determinado nivel de confianza, se encuentra el valor promedio de la variable respuesta.
# Predicciones con intervalo de confianza del 95%
# ==============================================================================
predicciones = modelo.get_prediction(exog=X_train).summary_frame(alpha=0.05)
predicciones['x'] = X_train.loc[:, 'bateos']
predicciones['y'] = y_train
predicciones = predicciones.sort_values('x')
# Gráfico del modelo
# ==============================================================================
fig, ax = plt.subplots(figsize=(6, 3.84))
ax.scatter(predicciones['x'], predicciones['y'], marker='o', color = "gray")
ax.plot(predicciones['x'], predicciones["mean"], linestyle='-', label="OLS")
ax.plot(predicciones['x'], predicciones["mean_ci_lower"], linestyle='--', color='blue', label="95% CI")
ax.plot(predicciones['x'], predicciones["mean_ci_upper"], linestyle='--', color='blue')
ax.fill_between(predicciones['x'], predicciones["mean_ci_lower"], predicciones["mean_ci_upper"], alpha=0.3)
ax.legend();
Error de test¶
# Error de test del modelo
# ==============================================================================
X_test = sm.add_constant(X_test, prepend=True)
predicciones = modelo.predict(exog=X_test)
rmse = root_mean_squared_error(y_true=y_test, y_pred=predicciones)
print(f"El error (rmse) de test es: {rmse}")
El error (rmse) de test es: 59.33671608336119
Interpretación¶
print(modelo.summary())
OLS Regression Results
==============================================================================
Dep. Variable: runs R-squared: 0.271
Model: OLS Adj. R-squared: 0.238
Method: Least Squares F-statistic: 8.191
Date: Thu, 13 Feb 2025 Prob (F-statistic): 0.00906
Time: 18:04:39 Log-Likelihood: -134.71
No. Observations: 24 AIC: 273.4
Df Residuals: 22 BIC: 275.8
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -2367.7028 1066.357 -2.220 0.037 -4579.192 -156.214
bateos 0.5529 0.193 2.862 0.009 0.152 0.953
==============================================================================
Omnibus: 5.033 Durbin-Watson: 1.902
Prob(Omnibus): 0.081 Jarque-Bera (JB): 3.170
Skew: 0.829 Prob(JB): 0.205
Kurtosis: 3.650 Cond. No. 4.17e+05
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 4.17e+05. This might indicate that there are
strong multicollinearity or other numerical problems.
La columna (coef) devuelve el valor estimado para los dos parámetros de la ecuación del modelo lineal ($\hat{\beta}_0$ y $\hat{\beta}_1$) que equivalen a la ordenada en el origen (intercept o const) y a la pendiente.
Se muestran también los errores estándar, el valor del estadístico t y el p-value (dos colas) de cada uno de los dos parámetros. Esto permite determinar si los predictores son significativamente distintos de 0, es decir, que tienen importancia en el modelo. Para el modelo generado, tanto la ordenada en el origen como la pendiente son significativas (p-values < 0.05).
El valor de R-squared indica que el modelo es capaz de explicar el 27.1% de la variabilidad observada en la variable respuesta (runs). Además, el p-value obtenido en el test F (Prob (F-statistic) = 0.00906) indica que sí hay evidencias de que la varianza explicada por el modelo es superior a la esperada por azar (varianza total).
El modelo lineal generado sigue la ecuación:
$$\text{runs = -2367.7028 + 0.5529 bateos}$$Por cada unidad que se incrementa el número de bateos, el número de runs aumenta en promedio 0.5529 unidades.
El error de test del modelo es de 59.34. Las predicciones del modelo final se alejan en promedio 59.34 unidades del valor real.
Ejemplo regresión lineal múltiple¶
Supóngase que el departamento de ventas de una empresa quiere estudiar la influencia que tiene la publicidad a través de distintos canales sobre el número de ventas de un producto. Se dispone de un conjunto de datos que contiene los ingresos (en millones) conseguido por ventas en 200 regiones, así como la cantidad de presupuesto, también en millones, destinado a anuncios por radio, TV y periódicos en cada una de ellas.
Librerías¶
Las librerías utilizadas en este ejemplo son:
# Tratamiento de datos
# ==============================================================================
import pandas as pd
import numpy as np
# Gráficos
# ==============================================================================
import matplotlib.pyplot as plt
import seaborn as sns
# Preprocesado y modelado
# ==============================================================================
from scipy.stats import pearsonr
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.stats.anova import anova_lm
from scipy import stats
# Configuración matplotlib
# ==============================================================================
plt.style.use('fivethirtyeight')
plt.rcParams.update({'font.size': 10, 'lines.linewidth': 1.5})
# Configuración warnings
# ==============================================================================
import warnings
warnings.filterwarnings('ignore')
Datos¶
# Datos
# ==============================================================================
tv = [230.1, 44.5, 17.2, 151.5, 180.8, 8.7, 57.5, 120.2, 8.6, 199.8, 66.1, 214.7,
23.8, 97.5, 204.1, 195.4, 67.8, 281.4, 69.2, 147.3, 218.4, 237.4, 13.2,
228.3, 62.3, 262.9, 142.9, 240.1, 248.8, 70.6, 292.9, 112.9, 97.2, 265.6,
95.7, 290.7, 266.9, 74.7, 43.1, 228.0, 202.5, 177.0, 293.6, 206.9, 25.1,
175.1, 89.7, 239.9, 227.2, 66.9, 199.8, 100.4, 216.4, 182.6, 262.7, 198.9,
7.3, 136.2, 210.8, 210.7, 53.5, 261.3, 239.3, 102.7, 131.1, 69.0, 31.5,
139.3, 237.4, 216.8, 199.1, 109.8, 26.8, 129.4, 213.4, 16.9, 27.5, 120.5,
5.4, 116.0, 76.4, 239.8, 75.3, 68.4, 213.5, 193.2, 76.3, 110.7, 88.3, 109.8,
134.3, 28.6, 217.7, 250.9, 107.4, 163.3, 197.6, 184.9, 289.7, 135.2, 222.4,
296.4, 280.2, 187.9, 238.2, 137.9, 25.0, 90.4, 13.1, 255.4, 225.8, 241.7, 175.7,
209.6, 78.2, 75.1, 139.2, 76.4, 125.7, 19.4, 141.3, 18.8, 224.0, 123.1, 229.5,
87.2, 7.8, 80.2, 220.3, 59.6, 0.7, 265.2, 8.4, 219.8, 36.9, 48.3, 25.6, 273.7,
43.0, 184.9, 73.4, 193.7, 220.5, 104.6, 96.2, 140.3, 240.1, 243.2, 38.0, 44.7,
280.7, 121.0, 197.6, 171.3, 187.8, 4.1, 93.9, 149.8, 11.7, 131.7, 172.5, 85.7,
188.4, 163.5, 117.2, 234.5, 17.9, 206.8, 215.4, 284.3, 50.0, 164.5, 19.6, 168.4,
222.4, 276.9, 248.4, 170.2, 276.7, 165.6, 156.6, 218.5, 56.2, 287.6, 253.8, 205.0,
139.5, 191.1, 286.0, 18.7, 39.5, 75.5, 17.2, 166.8, 149.7, 38.2, 94.2, 177.0,
283.6, 232.1]
radio = [37.8, 39.3, 45.9, 41.3, 10.8, 48.9, 32.8, 19.6, 2.1, 2.6, 5.8, 24.0, 35.1,
7.6, 32.9, 47.7, 36.6, 39.6, 20.5, 23.9, 27.7, 5.1, 15.9, 16.9, 12.6, 3.5,
29.3, 16.7, 27.1, 16.0, 28.3, 17.4, 1.5, 20.0, 1.4, 4.1, 43.8, 49.4, 26.7,
37.7, 22.3, 33.4, 27.7, 8.4, 25.7, 22.5, 9.9, 41.5, 15.8, 11.7, 3.1, 9.6,
41.7, 46.2, 28.8, 49.4, 28.1, 19.2, 49.6, 29.5, 2.0, 42.7, 15.5, 29.6, 42.8,
9.3, 24.6, 14.5, 27.5, 43.9, 30.6, 14.3, 33.0, 5.7, 24.6, 43.7, 1.6, 28.5,
29.9, 7.7, 26.7, 4.1, 20.3, 44.5, 43.0, 18.4, 27.5, 40.6, 25.5, 47.8, 4.9,
1.5, 33.5, 36.5, 14.0, 31.6, 3.5, 21.0, 42.3, 41.7, 4.3, 36.3, 10.1, 17.2,
34.3, 46.4, 11.0, 0.3, 0.4, 26.9, 8.2, 38.0, 15.4, 20.6, 46.8, 35.0, 14.3,
0.8, 36.9, 16.0, 26.8, 21.7, 2.4, 34.6, 32.3, 11.8, 38.9, 0.0, 49.0, 12.0,
39.6, 2.9, 27.2, 33.5, 38.6, 47.0, 39.0, 28.9, 25.9, 43.9, 17.0, 35.4, 33.2,
5.7, 14.8, 1.9, 7.3, 49.0, 40.3, 25.8, 13.9, 8.4, 23.3, 39.7, 21.1, 11.6, 43.5,
1.3, 36.9, 18.4, 18.1, 35.8, 18.1, 36.8, 14.7, 3.4, 37.6, 5.2, 23.6, 10.6, 11.6,
20.9, 20.1, 7.1, 3.4, 48.9, 30.2, 7.8, 2.3, 10.0, 2.6, 5.4, 5.7, 43.0, 21.3, 45.1,
2.1, 28.7, 13.9, 12.1, 41.1, 10.8, 4.1, 42.0, 35.6, 3.7, 4.9, 9.3, 42.0, 8.6]
periodico = [69.2, 45.1, 69.3, 58.5, 58.4, 75.0, 23.5, 11.6, 1.0, 21.2, 24.2, 4.0,
65.9, 7.2, 46.0, 52.9, 114.0, 55.8, 18.3, 19.1, 53.4, 23.5, 49.6, 26.2,
18.3, 19.5, 12.6, 22.9, 22.9, 40.8, 43.2, 38.6, 30.0, 0.3, 7.4, 8.5, 5.0,
45.7, 35.1, 32.0, 31.6, 38.7, 1.8, 26.4, 43.3, 31.5, 35.7, 18.5, 49.9,
36.8, 34.6, 3.6, 39.6, 58.7, 15.9, 60.0, 41.4, 16.6, 37.7, 9.3, 21.4, 54.7,
27.3, 8.4, 28.9, 0.9, 2.2, 10.2, 11.0, 27.2, 38.7, 31.7, 19.3, 31.3, 13.1,
89.4, 20.7, 14.2, 9.4, 23.1, 22.3, 36.9, 32.5, 35.6, 33.8, 65.7, 16.0, 63.2,
73.4, 51.4, 9.3, 33.0, 59.0, 72.3, 10.9, 52.9, 5.9, 22.0, 51.2, 45.9, 49.8,
100.9, 21.4, 17.9, 5.3, 59.0, 29.7, 23.2, 25.6, 5.5, 56.5, 23.2, 2.4, 10.7,
34.5, 52.7, 25.6, 14.8, 79.2, 22.3, 46.2, 50.4, 15.6, 12.4, 74.2, 25.9, 50.6,
9.2, 3.2, 43.1, 8.7, 43.0, 2.1, 45.1, 65.6, 8.5, 9.3, 59.7, 20.5, 1.7, 12.9,
75.6, 37.9, 34.4, 38.9, 9.0, 8.7, 44.3, 11.9, 20.6, 37.0, 48.7, 14.2, 37.7,
9.5, 5.7, 50.5, 24.3, 45.2, 34.6, 30.7, 49.3, 25.6, 7.4, 5.4, 84.8, 21.6, 19.4,
57.6, 6.4, 18.4, 47.4, 17.0, 12.8, 13.1, 41.8, 20.3, 35.2, 23.7, 17.6, 8.3,
27.4, 29.7, 71.8, 30.0, 19.6, 26.6, 18.2, 3.7, 23.4, 5.8, 6.0, 31.6, 3.6, 6.0,
13.8, 8.1, 6.4, 66.2, 8.7]
ventas = [22.1, 10.4, 9.3, 18.5, 12.9, 7.2, 11.8, 13.2, 4.8, 10.6, 8.6, 17.4, 9.2, 9.7,
19.0, 22.4, 12.5, 24.4, 11.3, 14.6, 18.0, 12.5, 5.6, 15.5, 9.7, 12.0, 15.0, 15.9,
18.9, 10.5, 21.4, 11.9, 9.6, 17.4, 9.5, 12.8, 25.4, 14.7, 10.1, 21.5, 16.6, 17.1,
20.7, 12.9, 8.5, 14.9, 10.6, 23.2, 14.8, 9.7, 11.4, 10.7, 22.6, 21.2, 20.2, 23.7,
5.5, 13.2, 23.8, 18.4, 8.1, 24.2, 15.7, 14.0, 18.0, 9.3, 9.5, 13.4, 18.9, 22.3,
18.3, 12.4, 8.8, 11.0, 17.0, 8.7, 6.9, 14.2, 5.3, 11.0, 11.8, 12.3, 11.3, 13.6,
21.7, 15.2, 12.0, 16.0, 12.9, 16.7, 11.2, 7.3, 19.4, 22.2, 11.5, 16.9, 11.7, 15.5,
25.4, 17.2, 11.7, 23.8, 14.8, 14.7, 20.7, 19.2, 7.2, 8.7, 5.3, 19.8, 13.4, 21.8,
14.1, 15.9, 14.6, 12.6, 12.2, 9.4, 15.9, 6.6, 15.5, 7.0, 11.6, 15.2, 19.7, 10.6,
6.6, 8.8, 24.7, 9.7, 1.6, 12.7, 5.7, 19.6, 10.8, 11.6, 9.5, 20.8, 9.6, 20.7, 10.9,
19.2, 20.1, 10.4, 11.4, 10.3, 13.2, 25.4, 10.9, 10.1, 16.1, 11.6, 16.6, 19.0, 15.6,
3.2, 15.3, 10.1, 7.3, 12.9, 14.4, 13.3, 14.9, 18.0, 11.9, 11.9, 8.0, 12.2, 17.1,
15.0, 8.4, 14.5, 7.6, 11.7, 11.5, 27.0, 20.2, 11.7, 11.8, 12.6, 10.5, 12.2, 8.7,
26.2, 17.6, 22.6, 10.3, 17.3, 15.9, 6.7, 10.8, 9.9, 5.9, 19.6, 17.3, 7.6, 9.7, 12.8,
25.5, 13.4]
datos = pd.DataFrame({'tv': tv, 'radio': radio, 'periodico': periodico, 'ventas': ventas})
Relación entre variables¶
El primer paso a la hora de establecer un modelo lineal múltiple es estudiar la relación que existe entre variables. Esta información es crítica a la hora de identificar cuáles pueden ser los mejores predictores para el modelo, y para detectar colinealidad entre predictores. A modo complementario, es recomendable representar la distribución de cada variable.
# Correlación entre columnas numéricas
# ==============================================================================
def tidy_corr_matrix(corr_mat):
'''
Función para convertir una matriz de correlación de pandas en formato tidy
'''
corr_mat = corr_mat.stack().reset_index()
corr_mat.columns = ['variable_1','variable_2','r']
corr_mat = corr_mat.loc[corr_mat['variable_1'] != corr_mat['variable_2'], :]
corr_mat['abs_r'] = np.abs(corr_mat['r'])
corr_mat = corr_mat.sort_values('abs_r', ascending=False)
return corr_mat
corr_matrix = datos.select_dtypes(include=['float64', 'int']).corr(method='pearson')
tidy_corr_matrix(corr_matrix).head(10)
| variable_1 | variable_2 | r | abs_r | |
|---|---|---|---|---|
| 3 | tv | ventas | 0.782224 | 0.782224 |
| 12 | ventas | tv | 0.782224 | 0.782224 |
| 7 | radio | ventas | 0.576223 | 0.576223 |
| 13 | ventas | radio | 0.576223 | 0.576223 |
| 6 | radio | periodico | 0.354104 | 0.354104 |
| 9 | periodico | radio | 0.354104 | 0.354104 |
| 11 | periodico | ventas | 0.228299 | 0.228299 |
| 14 | ventas | periodico | 0.228299 | 0.228299 |
| 2 | tv | periodico | 0.056648 | 0.056648 |
| 8 | periodico | tv | 0.056648 | 0.056648 |
# Heatmap matriz de correlaciones
# ==============================================================================
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(4, 4))
sns.heatmap(
corr_matrix,
annot = True,
cbar = False,
annot_kws = {"size": 8},
vmin = -1,
vmax = 1,
center = 0,
cmap = sns.diverging_palette(20, 220, n=200),
square = True,
ax = ax
)
ax.set_xticklabels(
ax.get_xticklabels(),
rotation = 45,
horizontalalignment = 'right',
)
ax.tick_params(labelsize = 10)
# Gráfico de distribución para cada variable numérica
# ==============================================================================
# Ajustar número de subplots en función del número de columnas
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(7, 4))
axes = axes.flat
columnas_numeric = datos.select_dtypes(include=['float64', 'int']).columns
for i, colum in enumerate(columnas_numeric):
sns.histplot(
data = datos,
x = colum,
stat = "count",
kde = True,
color = (list(plt.rcParams['axes.prop_cycle']) * 2)[i]["color"],
line_kws= {'linewidth': 2},
alpha = 0.3,
ax = axes[i]
)
axes[i].set_title(colum, fontsize = 8, fontweight = "bold")
axes[i].tick_params(labelsize = 8)
axes[i].set_xlabel("")
axes[i].set_ylabel("")
fig.tight_layout()
plt.subplots_adjust(top = 0.9)
fig.suptitle('Distribución variables numéricas', fontsize = 10, fontweight = "bold");
Ajuste del modelo¶
Se ajusta un modelo lineal múltiple con el objetivo de predecir las ventas en función de la inversión en los tres canales de publicidad.
# División de los datos en train y test
# ==============================================================================
X = datos[['tv', 'radio', 'periodico']]
y = datos['ventas']
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
train_size = 0.8,
random_state = 1234,
shuffle = True
)
# Crear y entrenar el modelo
# ==============================================================================
# A la matriz de predictores se le añade una columna de 1s para el intercept del modelo
X_train = sm.add_constant(X_train, prepend=True)
modelo = sm.OLS(endog=y_train, exog=X_train,)
modelo = modelo.fit()
print(modelo.summary())
OLS Regression Results
==============================================================================
Dep. Variable: ventas R-squared: 0.894
Model: OLS Adj. R-squared: 0.892
Method: Least Squares F-statistic: 437.8
Date: Thu, 13 Feb 2025 Prob (F-statistic): 1.01e-75
Time: 18:04:41 Log-Likelihood: -308.29
No. Observations: 160 AIC: 624.6
Df Residuals: 156 BIC: 636.9
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 2.8497 0.365 7.803 0.000 2.128 3.571
tv 0.0456 0.002 28.648 0.000 0.042 0.049
radio 0.1893 0.009 20.024 0.000 0.171 0.208
periodico 0.0024 0.007 0.355 0.723 -0.011 0.016
==============================================================================
Omnibus: 53.472 Durbin-Watson: 2.153
Prob(Omnibus): 0.000 Jarque-Bera (JB): 147.411
Skew: -1.353 Prob(JB): 9.77e-33
Kurtosis: 6.846 Cond. No. 472.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
El modelo con todas las variables introducidas como predictores tiene un $R^2$ alto (0.894), es capaz de explicar el 89.4% de la variabilidad observada en las ventas. El p-value del modelo es significativo (1.01e-75) por lo que se puede aceptar que el modelo es mejor que lo esperado es por azar, al menos uno de los coeficientes parciales de regresión es distinto de 0.
Acorde al p-value obtenido para el coeficiente parcial de regresión de periodico (0.723), esta variable no contribuye de forma significativa al modelo. Se entrena de nuevo el modelo, pero esta vez excluyendo el predictor periodico.
# Se elimina la columna periodico del conjunto de train y test
X_train = X_train.drop(columns = 'periodico')
X_test = X_test.drop(columns = 'periodico')
X_train = sm.add_constant(X_train, prepend=True)
modelo = sm.OLS(endog=y_train, exog=X_train,)
modelo = modelo.fit()
print(modelo.summary())
OLS Regression Results
==============================================================================
Dep. Variable: ventas R-squared: 0.894
Model: OLS Adj. R-squared: 0.892
Method: Least Squares F-statistic: 660.3
Date: Thu, 13 Feb 2025 Prob (F-statistic): 3.69e-77
Time: 18:04:41 Log-Likelihood: -308.36
No. Observations: 160 AIC: 622.7
Df Residuals: 157 BIC: 631.9
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 2.9004 0.335 8.652 0.000 2.238 3.563
tv 0.0456 0.002 28.751 0.000 0.042 0.049
radio 0.1904 0.009 21.435 0.000 0.173 0.208
==============================================================================
Omnibus: 54.901 Durbin-Watson: 2.157
Prob(Omnibus): 0.000 Jarque-Bera (JB): 156.962
Skew: -1.375 Prob(JB): 8.24e-35
Kurtosis: 6.998 Cond. No. 429.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Intervalos de confianza de los coeficientes¶
# Intervalos de confianza para los coeficientes del modelo
# ==============================================================================
intervalos_ci = modelo.conf_int(alpha=0.05)
intervalos_ci.columns = ['2.5%', '97.5%']
intervalos_ci
| 2.5% | 97.5% | |
|---|---|---|
| const | 2.238211 | 3.562549 |
| tv | 0.042439 | 0.048701 |
| radio | 0.172853 | 0.207942 |
Diagnóstico de los resíduos¶
# Diagnóstico errores (residuos) de las predicciones de entrenamiento
# ==============================================================================
prediccion_train = modelo.predict(exog=X_train)
residuos_train = prediccion_train - y_train
Inspección visual¶
# Gráficos
# ==============================================================================
fig, axes = plt.subplots(nrows=3, ncols=2, figsize=(8, 8))
axes[0, 0].scatter(y_train, prediccion_train, edgecolors=(0, 0, 0), alpha = 0.4)
axes[0, 0].plot([y_train.min(), y_train.max()], [y_train.min(), y_train.max()], 'k--', color = 'black', lw=2)
axes[0, 0].set_title('Valor predicho vs valor real', fontsize = 10, fontweight = "bold")
axes[0, 0].set_xlabel('Real')
axes[0, 0].set_ylabel('Predicción')
axes[0, 0].tick_params(labelsize = 7)
axes[0, 1].scatter(list(range(len(y_train))), residuos_train, edgecolors=(0, 0, 0), alpha = 0.4)
axes[0, 1].axhline(y = 0, linestyle = '--', color = 'black', lw=2)
axes[0, 1].set_title('Residuos del modelo', fontsize = 10, fontweight = "bold")
axes[0, 1].set_xlabel('id')
axes[0, 1].set_ylabel('Residuo')
axes[0, 1].tick_params(labelsize = 7)
sns.histplot(
data = residuos_train,
stat = "density",
kde = True,
line_kws= {'linewidth': 1},
alpha = 0.3,
ax = axes[1, 0]
)
axes[1, 0].set_title('Distribución residuos del modelo', fontsize = 10, fontweight = "bold")
axes[1, 0].set_xlabel("Residuo")
axes[1, 0].tick_params(labelsize = 7)
sm.qqplot(
residuos_train,
fit = True,
line = 'q',
ax = axes[1, 1],
alpha = 0.4,
lw = 2
)
axes[1, 1].set_title('Q-Q residuos del modelo', fontsize = 10, fontweight = "bold")
axes[1, 1].tick_params(labelsize = 7)
axes[2, 0].scatter(prediccion_train, residuos_train, edgecolors=(0, 0, 0), alpha = 0.4)
axes[2, 0].axhline(y = 0, linestyle = '--', color = 'black', lw=2)
axes[2, 0].set_title('Residuos del modelo vs predicción', fontsize = 10, fontweight = "bold")
axes[2, 0].set_xlabel('Predicción')
axes[2, 0].set_ylabel('Residuo')
axes[2, 0].tick_params(labelsize = 7)
# Se eliminan los axes vacíos
fig.delaxes(axes[2, 1])
fig.tight_layout()
plt.subplots_adjust(top=0.9)
fig.suptitle('Diagnóstico residuos', fontsize = 12, fontweight = "bold");
Los residuos no parecen distribuirse de forma aleatoria en torno a cero, sin mantener aproximadamente la misma variabilidad a lo largo del eje X. Este patrón apunta a una falta de homocedasticidad y de distribución normal.
Test de normalidad¶
Se comprueba si los residuos siguen una distribución normal empleando dos test estadísticos: Shapiro-Wilk test y D'Agostino's K-squared test. Este último es el que incluye el summary de statsmodels bajo el nombre de Omnibus.
En ambos test, la hipótesis nula considera que los datos siguen una distribución normal, por lo tanto, si el p-value no es inferior al nivel de referencia alpha seleccionado, no hay evidencias para descartar que los datos se distribuyen de forma normal.
# Normalidad de los residuos Shapiro-Wilk test
# ==============================================================================
shapiro_test = stats.shapiro(residuos_train)
shapiro_test
ShapiroResult(statistic=0.9165122842956668, pvalue=5.861065888990398e-08)
# Normalidad de los residuos D'Agostino's K-squared test
# ==============================================================================
k2, p_value = stats.normaltest(residuos_train)
print(f"Estadítico= {k2}, p-value = {p_value}")
Estadítico= 54.90105653039115, p-value = 1.197807558003796e-12
Ambos test muestran claras evidencias para rechazar la hipótesis de que los datos se distribuyen de forma normal (p-value << 0.01).
Predicciones¶
Una vez entrenado el modelo, se pueden obtener predicciones para nuevos datos. Los modelos de statsmodels permiten calcular los intervalos de confianza asociados a cada predicción.
# Predicciones con intervalo de confianza
# ==============================================================================
predicciones = modelo.get_prediction(exog=X_train).summary_frame(alpha=0.05)
predicciones.head(4)
| mean | mean_se | mean_ci_lower | mean_ci_upper | obs_ci_lower | obs_ci_upper | |
|---|---|---|---|---|---|---|
| 146 | 15.231643 | 0.248325 | 14.741154 | 15.722132 | 11.880621 | 18.582665 |
| 32 | 7.615382 | 0.247198 | 7.127119 | 8.103645 | 4.264685 | 10.966079 |
| 43 | 13.928155 | 0.213535 | 13.506384 | 14.349927 | 10.586500 | 17.269810 |
| 99 | 17.001020 | 0.210052 | 16.586127 | 17.415913 | 13.660226 | 20.341814 |
Error de test¶
# Error de test del modelo
# ==============================================================================
X_test = sm.add_constant(X_test, prepend=True)
predicciones = modelo.predict(exog = X_test)
rmse = root_mean_squared_error(y_true=y_test, y_pred=predicciones)
print(f"El error (rmse) de test es: {rmse}")
El error (rmse) de test es: 1.6956207500101192
Interpretación¶
El modelo de regresión lineal múltiple:
$$\text{ventas = 2.9004 + 0.0456tv + 0.1904radio}$$es capaz de explicar el 89.4% de la varianza observada en las ventas (R-squared: 0.894, Adj. R-squared: 0.892). El test $F$ es significativo (p-value: 3.69e-77). Por lo que hay evidencias claras de que el modelo es capaz de explicar la varianza en las ventas mejor de lo esperado por azar. Los test estadísticos para cada variable confirman que tv y radio están relacionadas con la cantidad de ventas y contribuyen al modelo.
No se satisfacen las condiciones de normalidad, por lo que los intervalos de confianza estimados para los coeficientes y las predicciones no son fiables.
El error (rmse) de test es de 1.696. Las predicciones del modelo final se alejan en promedio 1.696 unidades del valor real.
Interacción entre predictores¶
El modelo lineal a partir del cual se han obtenido las conclusiones asume que el efecto sobre las ventas debido a un incremento en el presupuesto de uno de los medios de comunicación es independiente del presupuesto gastado en los otros. Por ejemplo, el modelo lineal considera que el efecto promedio sobre las ventas debido a aumentar en una unidad el presupuesto de anuncios en TV es siempre de 0.0456, independientemente de la cantidad invertida en anuncios por radio. Sin embargo, esto no tiene por qué ser necesariamente así, puede existir interacción entre los predictores de forma que, el efecto de cada uno de ellos sobre la variable respuesta, depende en cierta medida del valor que tome el otro predictor.
Tal y como se ha definido previamente, un modelo lineal con dos predictores sigue la ecuación:
$$y=\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2}+\epsilon$$Acorde a esta definición, el incremento de una unidad en el predictor $x_1$ produce un incremento promedio de la variable y de $\beta_{1}$. Modificaciones en el predictor $x_2$ no alteran este hecho, y lo mismo ocurre con $x_2$ respecto a $x_1$. Para que el modelo pueda contemplar la interacción entre ambos, se introduce un tercer predictor, llamado interaction term, que se construye con el producto de los predictores $x_1$ y $x_2$.
$$y=\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2}+\beta_{3}x_{1}x_{2} + e$$La reorganización de los términos resulta en:
$$y=\beta_{0}+(\beta_{1} + \beta_{3}x_2)x_{1}+\beta_{2}x_{2}+ e$$El efecto de $x_{1}$ sobre $y$ ya no es constante, sino que depende del valor que tome $x_{2}$.
En los modelos de regresión lineal múltiple que incorporan interacciones entre predictores hay que tener en cuenta el hierarchical principle, según el cual, si se incorpora al modelo una interacción entre predictores, se deben incluir siempre los predictores individuales que participan en la interacción, independientemente de que su p-value sea significativo o no.
En stastmodels se puede introducir interacción entre predictores de dos formas:
Indicandolo en la fórmula con el término
*:ventas ~ tv * radioAñadiendo una nueva columna con la multiplicación de los predictores cuya interacción se quiere incluir en el modelo.
# División de los datos en train y test
# ==============================================================================
X = datos[['tv', 'radio']]
y = datos['ventas']
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
train_size = 0.8,
random_state = 1234,
shuffle = True
)
# Creación del modelo con interacciones utilizando matrices
# ==============================================================================
# Se añade una nueva columna con la interacción
X_train['tv_radio'] = X_train['tv'] * X_train['radio']
X_test['tv_radio'] = X_test['tv'] * X_test['radio']
X_train = sm.add_constant(X_train, prepend=True)
modelo_interacion = sm.OLS(endog=y_train, exog=X_train,)
modelo_interacion = modelo_interacion.fit()
print(modelo_interacion.summary())
OLS Regression Results
==============================================================================
Dep. Variable: ventas R-squared: 0.968
Model: OLS Adj. R-squared: 0.967
Method: Least Squares F-statistic: 1562.
Date: Thu, 13 Feb 2025 Prob (F-statistic): 4.28e-116
Time: 18:04:43 Log-Likelihood: -212.91
No. Observations: 160 AIC: 433.8
Df Residuals: 156 BIC: 446.1
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 6.9035 0.281 24.558 0.000 6.348 7.459
tv 0.0183 0.002 10.812 0.000 0.015 0.022
radio 0.0261 0.010 2.623 0.010 0.006 0.046
tv_radio 0.0011 5.86e-05 18.931 0.000 0.001 0.001
==============================================================================
Omnibus: 121.946 Durbin-Watson: 1.686
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1473.094
Skew: -2.642 Prob(JB): 0.00
Kurtosis: 16.894 Cond. No. 1.84e+04
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.84e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
Los resultados muestran una evidencia clara de que la interacción tv radio es significativa (p-value* muy próximo a 0).
El modelo que incorpora la interacción tiene un Adjusted R-squared de 0.967, un valor superior al 0.892 del modelo que solo contemplaba el efecto de los predictores por separado. Ahora bien, ¿Es suficiente esta diferencia para afirmar que el modelo con interacción es superior? Una forma de responder a esta pregunta es recurriendo al F-test (ANOVA).
Comparación de modelos mediante test F-test (ANOVA)¶
Supóngase un modelo $M$ y otro modelo $m$, de menor tamaño, formado por un subconjunto de los predictores contenidos en $M$. Si la diferencia en el ajuste es muy pequeña, acorde al principio de parsimonia, el modelo $m$ es más adecuado. Es posible contrastar si la diferencia en ajuste es significativa mediante la comparación de los residuos. En concreto el estadístico empleado es:
$$\frac{RSS_m - RSS_M}{RSS_M}$$Para evitar que el tamaño del modelo influya en el contraste, se divide la suma de residuos cuadrados RSS de cada modelo entre sus grados de libertad. El estadístico resultante sigue una distribución $F$.
$$\frac{(RSS_m - RSS_M)/(df_m - df_M)}{RSS_M/(df_M)} \sim F_{df_m-df_M, \ df_M}$$donde $df$ son los grados de libertad del modelo, que equivalen al número de observaciones menos el número de predictores.
En los apartados anteriores, se entrenó un modelo que incluía interacciones y otro que no. Se procede a realizar un test de hipótesis que evalúe la hipótesis nula de que ambos modelos se ajustan a los datos igual de bien. Es decir, que permita determinar si un modelo es mejor que el otro prediciendo la variable respuesta. Esto puede hacerse con la función anova_lm() de statsmodels.stats.anova.
anova_lm(modelo, modelo_interacion)
| df_resid | ssr | df_diff | ss_diff | F | Pr(>F) | |
|---|---|---|---|---|---|---|
| 0 | 157.0 | 442.212726 | 0.0 | NaN | NaN | NaN |
| 1 | 156.0 | 134.116584 | 1.0 | 308.096142 | 358.3673 | 2.926598e-42 |
El test ANOVA encuentra evidencias claras (p-value prácticamente de cero) de que el modelo que incluye la interacción entre predictores es capaz de modelar mejor la variable respuesta.
Esta forma de comparar modelos está muy arraigada en la comunidad estadística. En la comunidad de machine learning es mucho más común comparar modelos con técnicas de validación como la validación cruzada.
Apuntes varios¶
En este apartado recojo comentarios, definiciones y puntualizaciones que he ido encontrando en diferentes fuentes y que he considerado mejor mantenerlos información complementaria.
Origen del método de mínimos cuadrados y regresión¶
Linear Models with R, by Julian J. Faraway
El método de mínimos cuadrados fue publicado en 1805 por Adrien Marie Legendre. El término regresión proviene de la publicación que hizo Francis Galton en 1985 llamada Regression to mediocrity. En ella, Galton emplea el método de mínimos cuadrados para demostrar que los hijos de parejas altas tienden a ser también altos pero no tanto como sus padres y que los hijos de parejas de poca estatura tienden a ser bajos pero no tanto como sus padres.
Estimación de la varianza de un modelo lineal por mínimos cuadrados¶
Linear Models with R, by Julian J. Faraway
La estimación de la varianza ($\sigma^2$) de un modelo lineal obtenido por mínimos cuadrados es:
$$\sigma^2 = \frac{RSS}{n - p}$$El término Residual Standar Error (RSE), es la raíz cuadrada de $\sigma^2$:
$$RSE = \sqrt{\frac{RSS}{n - p}}$$Ventajas del método de mínimos cuadrados para estimar los coeficientes de un modelo lineal¶
Linear Models with R, by Julian J. Faraway
Si bien existen alternativas al método de mínimos cuadrados para obtener la estimación de los coeficientes de correlación $\hat{\beta}_j$ de un modelo lineal, este presenta una serie de ventajas:
Tiene una interpretación geométrica, lo que facilita su comprensión.
Si los errores son independientes y se distribuyen de forma normal, su solución equivale a la estimación de máxima verosimilitud (likelihood).
Los $\hat{\beta}_j$ son estimaciones insesgadas.
Identidad (identifiability) o colinealidad¶
Linear Models with R, by Julian J. Faraway
El método de mínimos cuadrados tiene una solución única solo si la matriz formada por los predictores es de rango máximo, es decir, que todas sus columnas (predictores) son linealmente independientes. En la práctica, esta condición de identidad suele violarse con frecuencia. Los siguientes son algunos escenarios en los que ocurre:
Cuando uno de los predictores introducidos en el modelo es una transformación lineal o combinación de otros predictores presentes en el modelo. Por ejemplo, que la variable peso se introduzca en Kg y en libras o que se introduzcan como predictores el número de años de educación básica, el número de años de educación universitaria y el total de años de educación. Este problema se puede evitar estudiando la naturaleza de las variables disponibles y su relación.
Sobresaturación del modelo, cuando hay más predictores que observaciones.
Precaución al evaluar la normalidad de los residuos por contraste de hipótesis¶
Linear Models with R, by Julian J. Faraway
Que los residuos de un modelo de regresión lineal se distribuyan de forma normal es una condición necesaria para que la significancia (p-value) y los intervalos de confianza asociados a los predictores (calculados a partir de modelos teóricos) sean precisos. Con frecuencia, esta condición se evalúa con contrastes de hipótesis tales como el Shapiro-Wilk test. Cuando esto ocurre, es importante entender la relación entre p-value y tamaño de muestra. A mayor número de residuos mayor potencia tiene el test y, por lo tanto, pequeñas desviaciones de la normalidad resultan significativas. A su vez, el teorema del límite central indica que, cuanto mayor el tamaño de la muestra, más robustos son los resultados frente a desviaciones de la normalidad. Dadas estas propiedades, suele ser más recomendable evaluar la normalidad de los residuos de forma gráfica mediante representación de los cuantiles teóricos qq-plot.
Transformación de variables¶
Linear Models with R, by Julian J. Faraway y wikipedia
Transformar la variable respuesta o los predictores puede ser una forma de mejorar el ajuste de un modelo o corregir la violación de alguna de las condiciones de regresión.
Cuando la transformación se aplica a la variable respuesta, es importante recordar que las predicciones generadas por el modelo están en escala transformada. Una vez calculada la predicción, se puede transformar de vuelta a la escala original. Esto mismo aplica a los intervalos de confianza, primero se calculan los límites (superior e inferior) y luego se convierten de vuelta. En contraposición, los coeficientes de regresión obtenidos para los predictores se tienen que interpretar en el contexto de la transformación, no es posible aplicarles la inversa de la transformación e interpretarlos en la escala original.
Transformación de Box-Cox
La transformación exponencial de la variable respuesta ($y^{\lambda}$) es con frecuencia una solución útil para mejorar los modelos, sin embargo, identificar el valor óptimo del exponente no es siempre inmediato. El método de Box-Cox permite encontrar si existe algún valor al que se pueda elevar la variable respuesta para mejorar el ajuste del modelo y, en tal caso, identificar cual es. Acorde a este método, se busca una transformación $y \rightarrow g_{\lambda}(y)$ tal que:
$$ g_{\lambda}(y) = \begin{cases} \frac{y^{\lambda}-1}{\lambda} & \text{si } \lambda \neq 0 \\ \log(y) & \text{si } \lambda = 0 \end{cases} $$Cuando el objetivo del modelo es predictivo, se puede simplificar $\frac{y^{\lambda}-1}{y}$ por $y^{\lambda}$.
El valor de $\lambda$ óptimo se identifica por máxima verosimilitud: se selecciona un intervalo de valores de $\lambda$, para cada valor se realiza la transformación y se calculan los cuadrados de los residuos. Aquel que tenga el menor valor de la suma de residuales será la mejor opción.
La transformación de la variable respuesta puede hacer que el modelo sea más difícil de interpretar, por lo que no es aconsejable a no ser que sea realmente necesaria. Para asegurarse de que lo es, además de calcular el valor óptimo de $\lambda$, se puede estimar su intervalo de confianza del 95%. Si este incluye el valor $\lambda=1$ no hay evidencias suficientes a favor de la transformación. Cuando la transformación sí es necesaria, se aconseja elegir dentro del intervalo de confianza, aquel valor que facilite la interpretación del modelo. Por ejemplo, si el intervalo es [-0.7, 0.7], el valor 0.5 es el más adecuado ya que se corresponde con $\sqrt(y)$.
La transformación Box-Cox solo es aplicable cuando la variable respuesta toma siempre valores positivos. Si algún $y_i < 0$, se puede sumar una constante a $y$ para que sea positiva, pero es una solución poco elegante. Otra característica de este tipo de transformación es que se ve altamente influenciada por outliers, haciendo que los valores absolutos de $\lambda$ sean sospechosamente altos.
Transformación logarítmica
Existen múltiples alternativas a la transformación exponencial Box-Cox. Una de ellas consiste en sumarle una constante a la variable respuesta y aplicarle logaritmos, $g_{\alpha} = log(y + \alpha)$.
Interpretación de los coeficientes de regresión de un modelo lineal¶
Linear Models with R, by Julian J. Faraway
Cuando se emplea un modelo de regresión lineal para extraer información sobre la relación existente entre los predictores y la variable respuesta, hay que ser cautelosos y no llegar a conclusiones que van más allá de lo que dice el modelo.
El set de datos gala del paquete faraway contiene información sobre las islas que forman el archipiélago de las Galápagos. Entre las variables almacenadas están: número de especies que habitan la isla (Species), el área (Area) y altura (Elevation) de la isla, la distancia a la isla más próxima (Nearest), la distancia a la isla Santa Cruz (Scruz) y el área de la isla adyacente (Adjacent). Se quiere emplear un modelo de regresión lineal para estudiar la relación que tiene el predictor Elevation con el número de especies que hay en la isla.
url = "https://raw.githubusercontent.com/JoaquinAmatRodrigo/Estadistica-machine-learning-python/" + \
"master/data/gala_faraway.csv"
datos = pd.read_csv(url)
datos.head(3)
| Island | Species | Endemics | Area | Elevation | Nearest | Scruz | Adjacent | |
|---|---|---|---|---|---|---|---|---|
| 0 | Baltra | 58 | 23 | 25.09 | 346 | 0.6 | 0.6 | 1.84 |
| 1 | Bartolome | 31 | 21 | 1.24 | 109 | 0.6 | 26.3 | 572.33 |
| 2 | Caldwell | 3 | 3 | 0.21 | 114 | 2.8 | 58.7 | 0.78 |
modelo = smf.ols(
formula = 'Species ~ Area + Elevation + Nearest + Scruz + Adjacent',
data = datos
)
modelo = modelo.fit()
print(modelo.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Species R-squared: 0.766
Model: OLS Adj. R-squared: 0.717
Method: Least Squares F-statistic: 15.70
Date: Thu, 13 Feb 2025 Prob (F-statistic): 6.84e-07
Time: 18:04:43 Log-Likelihood: -162.54
No. Observations: 30 AIC: 337.1
Df Residuals: 24 BIC: 345.5
Df Model: 5
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 7.0682 19.154 0.369 0.715 -32.464 46.601
Area -0.0239 0.022 -1.068 0.296 -0.070 0.022
Elevation 0.3195 0.054 5.953 0.000 0.209 0.430
Nearest 0.0091 1.054 0.009 0.993 -2.166 2.185
Scruz -0.2405 0.215 -1.117 0.275 -0.685 0.204
Adjacent -0.0748 0.018 -4.226 0.000 -0.111 -0.038
==============================================================================
Omnibus: 12.683 Durbin-Watson: 2.476
Prob(Omnibus): 0.002 Jarque-Bera (JB): 13.498
Skew: 1.136 Prob(JB): 0.00117
Kurtosis: 5.374 Cond. No. 1.90e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.9e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
Si se interpreta el coeficiente de regresión como que, por cada unidad que aumenta Elevation, el número de especies se incrementa en promedio 0.3195 unidades, se estaría estableciendo una conclusión errónea. De hecho, si utilizando los mismos datos se ajusta un modelo más sencillo, el valor del coeficiente cambia.
modelo = smf.ols(
formula = 'Species ~ Elevation',
data = datos
)
modelo = modelo.fit()
print(modelo.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Species R-squared: 0.545
Model: OLS Adj. R-squared: 0.529
Method: Least Squares F-statistic: 33.59
Date: Thu, 13 Feb 2025 Prob (F-statistic): 3.18e-06
Time: 18:04:43 Log-Likelihood: -172.49
No. Observations: 30 AIC: 349.0
Df Residuals: 28 BIC: 351.8
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 11.3351 19.205 0.590 0.560 -28.005 50.675
Elevation 0.2008 0.035 5.795 0.000 0.130 0.272
==============================================================================
Omnibus: 14.860 Durbin-Watson: 2.021
Prob(Omnibus): 0.001 Jarque-Bera (JB): 29.281
Skew: 0.878 Prob(JB): 4.38e-07
Kurtosis: 7.510 Cond. No. 741.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Esto ocurre porque el coeficiente de regresión de un determinado predictor siempre tiene que interpretarse en el contexto de los demás predictores incluidos en el modelo, puesto que influyen sobre él. La forma correcta es: el incremento en una unidad del predictor $x_j$ provoca un cambio promedio de $\hat{\beta}_j$ unidades en la variable respuesta, manteniéndose constantes el resto de predictores.
Con frecuencia, cuando la escala en la que se mide cada predictor es muy distinta (orden de magnitud), suelen estandarizarse los predictores previo ajuste del modelo. Si esto ocurre, la interpretación de los coeficientes de regresión pasa a ser: el incremento en una unidad estándar del predictor $x_j$ provoca un cambio promedio de $\hat{\beta}_j$ unidades estándar en la variable respuesta, manteniéndose constantes el resto de predictores.
En los estudios observacionales, raramente se pueden mantener constantes los predictores a voluntad del investigador, de ahí que sea difícil establecer relaciones de causalidad.
Test de permutación (simulación monte carlo) para la significancia del modelo y sus predictores¶
Linear Models with R, by Julian J. Faraway
El contraste de hipótesis basado en el F-test se fundamenta en el supuesto de que los residuos se distribuyen de forma normal. Si bien el teorema del límite central demuestra que, aun cuando la distribución se aleja de la normalidad, los resultados de la inferencia son buenos si el tamaño muestral es grande, no existe un tamaño exacto a partir del cual se garantice su validez. Los test de permutación ofrecen una alternativa que no requiere asumir la normalidad de los residuos.
Supóngase un modelo con dos predictores, Species ~ Nearest + Scruz, para el que se calcula el estadístico F. El p-value asociado indica cómo de probable es obtener un valor de F igual o más extremo si no existe relación entre la variable respuesta y los predictores. Cuando se cumple la condición de $\epsilon \sim N(0, \sigma^2)$, esta probabilidad se puede obtener de la F-distribution.
# Datos (dataset gala del paquete R faraway)
# ==============================================================================
url = "https://raw.githubusercontent.com/JoaquinAmatRodrigo/Estadistica-machine-learning-python/" + \
"master/data/gala_faraway.csv"
datos = pd.read_csv(url)
# Modelo
# ==============================================================================
modelo = smf.ols(formula = 'Species ~ Nearest + Scruz', data = datos)
modelo = modelo.fit()
# Estadístico teórico F y su p-value
# ==============================================================================
print(f"Estadístico F: {modelo.fvalue}")
print(f"P-value: {modelo.f_pvalue}")
Estadístico F: 0.6019558326652168 P-value: 0.5549254563908441
Cuando no se cumple la condición de normalidad, estos valores no son fiables. Una mejor aproximación es recurrir a un test de permutación. Para ello, se simula la hipótesis nula de "no asociación entre la variable respuesta y todos predictores", intercambiando aleatoriamente la variable respuesta entre las observaciones.
Si este proceso se repite suficientes veces (1000 - 10000), reajustando cada vez el modelo y almacenando el estadístico F, se puede calcular el porcentaje de casos en los que F ha resultado ser igual o mayor que el valor obtenido en el modelo inicial. Este porcentaje es la aproximación empírica del p-value.
# Test de permutaciones
# ==============================================================================
n_simulaciones = 5000
f_simulados = np.repeat(np.nan, n_simulaciones)
datos_temp = datos.copy()
for i in np.arange(n_simulaciones):
datos_temp["Species"] = datos['Species'].sample(frac=1).reset_index(drop=True)
modelo_temp = smf.ols(formula = 'Species ~ Nearest + Scruz', data = datos_temp)
modelo_temp = modelo_temp.fit()
f_simulados[i] = modelo_temp.fvalue
p_value_empirico = np.mean(f_simulados >= 0.6019558326652213)
print(f"p-value aproximado por test de permutación: {p_value_empirico}")
p-value aproximado por test de permutación: 0.5696
El p-value obtenido por permutaciones es muy similar al obtenido por el método teórico basado en normalidad (0.555).
El método de permutaciones presenta la ventaja de ser igual de bueno que el método teórico (si se realizan suficientes permutaciones) cuando se cumple la condición de normalidad y además se puede aplicar también cuando no se cumple. La desventaja es que requiere de mucha más computación.
La misma aproximación por permutaciones puede emplearse para determinar si un predictor en particular contribuye de forma significativa al modelo, o lo que es lo mismo, si está asociado a la variable respuesta. En este caso, se permuta únicamente el valor del predictor de interés, simulando así la hipótesis nula de que no existe asociación con la variable respuesta. En cada permutación se ajusta el modelo y se almacena el estadístico t obtenido para el predictor. Tras realizar suficientes permutaciones, se calcula el porcentaje de casos en los que el valor absoluto de t es igual o mayor al valor absoluto observado en el modelo inicial.
Supóngase un modelo con dos predictores, Species ~ Nearest + Scruz, para el que se quiere calcular la significancia del predictor Scruz.
# Modelo
# ==============================================================================
modelo = smf.ols(formula = 'Species ~ Nearest + Scruz', data = datos)
modelo = modelo.fit()
# Estadístico teórico t y su p-value para el predictor Scruz
# ==============================================================================
print(f"Estadístico t para Scruz: {modelo.tvalues['Scruz']}")
print(f"P-value para Scruz: {modelo.pvalues['Scruz']}")
Estadístico t para Scruz: -1.0946730850617026 P-value para Scruz: 0.2833295186486556
# Test de permutaciones
# ==============================================================================
n_simulaciones = 5000
t_simulados = np.repeat(np.nan, n_simulaciones)
datos_temp = datos.copy()
for i in np.arange(n_simulaciones):
datos_temp["Scruz"] = datos['Scruz'].sample(frac=1).reset_index(drop=True)
modelo_temp = smf.ols(formula = 'Species ~ Nearest + Scruz', data = datos_temp)
modelo_temp = modelo_temp.fit()
t_simulados[i] = modelo_temp.tvalues['Scruz']
p_value_empirico = np.mean(np.abs(t_simulados) >= np.abs(-1.094673085061703))
print(f"p-value aproximado por test de permutación: {p_value_empirico}")
p-value aproximado por test de permutación: 0.2746
El p-value obtenido por permutaciones es muy similar al obtenido por el método teórico basado en normalidad (0.2833).
Bootstrapping para calcular intervalos de confianza¶
Linear Models with R, by Julian J. Faraway
El método empleado por statsmodels y scikitlearn para calcular los intervalos de confianza de los coeficientes de regresión de un modelo lineal se basa en la distribución t-student y siguen la estructura:
Para que los intervalos basados en esta distribución teórica sean válidos, es necesario que los residuos del modelo se distribuyan de forma normal. Sí esto no ocurre, el método de bootstrapping ofrece una alternativa que no requiere de esta condición.
A continuación, se muestra un ejemplo de cómo aplicar este método para estimar los CI 95% del modelo Species ~ Area + Elevation + Nearest + Scruz + Adjacent. Para una descripción más detallada del bootstrapping consultar Resampling: Test de permutación, Simulación de Monte Carlo y Bootstrapping.
En el libro Linear Models with R by Julian J. Faraway se hace resampling sobre los residuos del modelo. A mi parecer es más intuitivo hacer el resampling sobre los pares (respuesta, predictores). Las estimaciones de los intervalos que se obtienen no son exactamente iguales, por lo que no puedo garantizar la validez de esta aproximación.
# Datos (dataset gala del paquete R faraway)
# ==============================================================================
url = "https://raw.githubusercontent.com/JoaquinAmatRodrigo/Estadistica-machine-learning-python/" + \
"master/data/gala_faraway.csv"
datos = pd.read_csv(url)
# Coeficientes e intervalos basados en distribución teórica
# ==============================================================================
modelo = smf.ols(
formula = 'Species ~ Area + Elevation + Nearest + Scruz + Adjacent',
data = datos
)
modelo = modelo.fit()
# Coeficientes
print("Coeficientes del modelo")
print(modelo.params)
# Intervalos del 95% para los coeficientes del modelo
print("")
print("Intervalos teóricos")
print(modelo.conf_int(alpha=0.05))
Coeficientes del modelo
Intercept 7.068221
Area -0.023938
Elevation 0.319465
Nearest 0.009144
Scruz -0.240524
Adjacent -0.074805
dtype: float64
Intervalos teóricos
0 1
Intercept -32.464101 46.600542
Area -0.070216 0.022339
Elevation 0.208710 0.430219
Nearest -2.166486 2.184774
Scruz -0.685093 0.204044
Adjacent -0.111336 -0.038273
# Intervalos estimados por bootstrapping
# ==============================================================================
n_simulaciones = 5000
# 6 = 5 predictores + 1 intercept
coef_simulados = np.zeros(shape= (n_simulaciones, 6), dtype=float)
for i in np.arange(n_simulaciones):
datos_temp = datos.sample(frac=1, replace=True)
modelo_temp = smf.ols(
formula = 'Species ~ Area + Elevation + Nearest + Scruz + Adjacent',
data = datos_temp
)
modelo_temp = modelo_temp.fit()
coef_simulados[i, :] = modelo_temp.params
# Cálculo de los del intervalo por quantiles 0.05 y 0.975
intervalos_empiricos = np.quantile(coef_simulados, q = [.025, 0.975], axis=0)
intervalos_empiricos = pd.DataFrame(
data = intervalos_empiricos,
index = ['2.5%', '97.5%'],
columns = modelo.conf_int().index
)
print("Intervalos empíricos")
intervalos_empiricos
Intervalos empíricos
| Intercept | Area | Elevation | Nearest | Scruz | Adjacent | |
|---|---|---|---|---|---|---|
| 2.5% | -29.799620 | -0.089498 | 0.048821 | -4.438021 | -0.638774 | -0.137678 |
| 97.5% | 35.338727 | 0.411985 | 0.501659 | 1.797487 | 0.341072 | 0.014511 |
Regresión robusta¶
El método de regresión por mínimos cuadrados ordinarios (OLS) descrito en los apartados anteriores asume que los residuos/errores son independientes, con varianza constante y que se distribuyen de forma normal. En la práctica, estas condiciones no se cumplen con frecuencia, lo que hace necesario disponer de métodos de ajuste alternativos. Algunos de ellos son: Robust Regression, Generalized Least Squares y Weighted Least Squares.
Robust Regression
Cuando los errores no siguen una distribución normal, los resultados obtenidos por mínimos cuadrados se ven afectados, siendo mayor el impacto cuanto más largas son las colas. Una solución simple pasa por eliminar los valores atípicos (outliers) que forman dichas colas, sin embargo, de confirmarse que no son errores de lectura, el modelo debería incluirlos puesto que son parte del fenómeno que se quiere estudiar. Robust regression consigue reducir la influencia de los valores atípicos en el ajuste del modelo. Los dos tipos de robust regression más empleados son: M-Estimation y Least Trimmed Squares.
M-Estimation: tiene diferentes variantes dependiendo de la función que se emplee para atenuar el peso de las observaciones extremas. El método de Huber consigue disminuir la influencia de valores atípicos siempre y cuando sean pocos y de una magnitud no excesiva.
Least Trimmed Squares: este tipo de robust regression ajusta el modelo mediante mínimos cuadrados pero empleando únicamente los q residuos de menor tamaño, ignorando por completo el resto de observaciones. Es por lo tanto más independiente de los valores atípicos que M-estimation, aunque depende del valor q que se especifique.
En la gran mayoría de ocasiones, los resultados obtenidos empleando robust regression son similares a los que se llega si se utiliza regresión por mínimos cuadrados y se analizan las observaciones atípicas o influyentes. Cuando este último análisis no se puede realizar, bien porque el investigador no sabe o bien porque se trata de un proceso automatizado, la robust regression es más segura.
Dada la rapidez con la que se pueden aplicar estos métodos de ajuste, se puede emplear robust regression como método de confirmación. Primero se ajusta el modelo empleando mínimos cuadrados y, si al compararlo con robust regression no hay grandes diferencias, significa que el modelo no contiene observaciones influyentes.
Generalized Least Squares
Es una alternativa a la regresión por mínimos cuadrados cuando existe correlación entre los residuos. Esto ocurre con frecuencia en series temporales.
Weighted Least Squares
Es una alternativa a la regresión por mínimos cuadrados que no se ve afectada por que los residuos no tengan varianza constante (falta de homocedasticidad). Algunos escenarios en los que suele ser recomendable su uso son:
Cuando los residuos son proporcionales a alguno de los predictores, es decir, a medida que aumenta el valor del predictor también lo hacen los residuos.
Cuando la variable $Y_i$ se ha obtenido a partir de $n_i$ observaciones (por ejemplo la media de $n$ repeticiones), dado que $Var(y_i) = \sigma^2/n_i$, puede ocurrir que la varianza sea proporcional al tamaño del grupo.
Cuando la variable respuesta procede de diferentes fuentes, por ejemplo diferentes instrumentos, cada una con una precisión distinta, se asigna a cada fuente $i$ un peso tal que $weight_i = 1/sd(y_i)$.
Información de sesión¶
import session_info
session_info.show(html=False)
----- matplotlib 3.9.2 numpy 1.26.0 pandas 2.2.3 scipy 1.14.1 seaborn 0.13.2 session_info 1.0.0 sklearn 1.5.1 statsmodels 0.14.3 ----- IPython 8.27.0 jupyter_client 8.6.3 jupyter_core 5.7.2 notebook 6.4.12 ----- Python 3.12.5 | packaged by Anaconda, Inc. | (main, Sep 12 2024, 18:27:27) [GCC 11.2.0] Linux-5.15.0-1075-aws-x86_64-with-glibc2.31 ----- Session information updated at 2025-02-13 18:06
Bibliografía¶
OpenIntro Statistics: Third Edition, David M Diez, Christopher D Barr, Mine Çetinkaya-Rundel
An Introduction to Statistical Learning: with Applications in R (Springer Texts in Statistics)
Linear Models with R, Julian J.Faraway
Points of Significance: Simple linear regression by Naomi Altman & Martin Krzywinski
Points of Significance: Multiple linear regression Martin Krzywinski & Naomi Altman
Métodos estadísticos en ingenieria Rafael Romero Villafranca, Luisa Rosa Zúnica Ramajo
Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825-2830, 2011.
Instrucciones para citar¶
¿Cómo citar este documento?
Si utilizas este documento o alguna parte de él, te agradecemos que lo cites. ¡Muchas gracias!
Regresión lineal con Python por Joaquín Amat Rodrigo, disponible con una licencia Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0 DEED) en https://cienciadedatos.net/documentos/py10-regresion-lineal-python.html
¿Te ha gustado el artículo? Tu ayuda es importante
Tu contribución me ayudará a seguir generando contenido divulgativo gratuito. ¡Muchísimas gracias! 😊
Este documento creado por Joaquín Amat Rodrigo tiene licencia Attribution-NonCommercial-ShareAlike 4.0 International.
Se permite:
-
Compartir: copiar y redistribuir el material en cualquier medio o formato.
-
Adaptar: remezclar, transformar y crear a partir del material.
Bajo los siguientes términos:
-
Atribución: Debes otorgar el crédito adecuado, proporcionar un enlace a la licencia e indicar si se realizaron cambios. Puedes hacerlo de cualquier manera razonable, pero no de una forma que sugiera que el licenciante te respalda o respalda tu uso.
-
No-Comercial: No puedes utilizar el material para fines comerciales.
-
Compartir-Igual: Si remezclas, transformas o creas a partir del material, debes distribuir tus contribuciones bajo la misma licencia que el original.

