Más sobre ciencia de datos y estadística en: cienciadedatos.net
- Ajuste y selección de distribuciones
- Kernel density estimation KDE
- Comparación de distribuciones con Python: test Kolmogorov–Smirnov
- Análisis de normalidad
- Análisis de homocedasticidad
- Correlación lineal
- Test de permutación
- Bootstrapping
- T-test
- ANOVA.
- U-test

Introducción¶
La técnica de análisis de varianza (ANOVA), desarrollada por Ronald Fisher, constituye la herramienta básica para el estudio del efecto de uno o más factores (cada uno con dos o más niveles) sobre la media de una variable continua. Es por lo tanto uno de los test estadísticos que se pueden emplear para comparar las medias de dos o más grupos.
La hipótesis nula de la que parten los diferentes tipos de ANOVA es que la media de la variable estudiada es la misma en los diferentes grupos, en contraposición a la hipótesis alternativa de que, al menos dos medias, difieren de forma significativa. ANOVA permite comparar múltiples medias, pero lo hace mediante el estudio de las varianzas.
La idea intuitiva detrás del funcionamiento básico de un ANOVA es la siguiente:
1) Calcular la media de cada uno de los grupos.
2) Calcular la varianza de las medias de los grupos. Esta es la varianza explicada por la variable grupo, y se le conoce como intervarianza.
3) Calcular las varianzas internas de cada grupo y obtener su promedio. Esta es la varianza no explicada por la variable grupo, y se le conoce como intravarianza.
Acorde a la hipótesis nula de que todas las observaciones proceden de la misma población (tienen la misma media y varianza), es de esperar que la intervarianza y la intravarianza sean iguales. A medida que las medias de los grupos se alejan las unas de las otras, la intervarianza aumenta y deja de ser igual a la intravarianza.
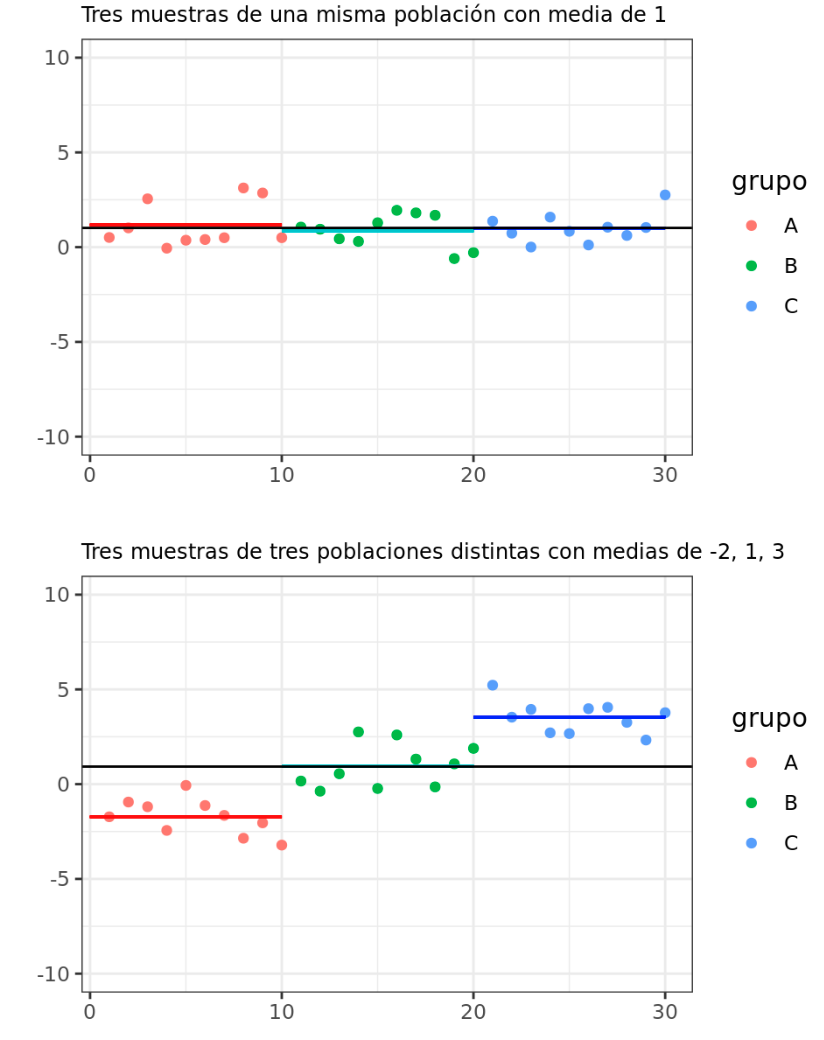
El estadístico estudiado en el ANOVA ($F_{ratio}$), se calcula como el ratio entre la varianza de las medias de los grupos (intervarianza) y el promedio de la varianza dentro de los grupos (intravarianza). Este estadístico sigue una distribución F de Fisher-Snedecor. Si se cumple la hipótesis nula, el estadístico $F$ adquiere el valor de 1 puesto que la intervarianza es igual a la intravarianza. A medida que las medias de los grupos se alejan entre ellas, mayor es la intervarianza en comparación a la intravarianza, lo que genera valores de $F$ superiores a 1, que tienen una probabilidad asociada menor (menor el p-value).
En concreto, si $S_1^2$ es la la varianza de una muestra de tamaño $N_1$ extraída de una población normal de varianza $\sigma_1^2$, y $S_2^2$ es la la varianza de una muestra de tamaño $N_2$ extraída de una población normal de varianza $\sigma_2^2$, y ambas muestras son independientes, el cociente:
$$F = \frac{S_1^2/\sigma_1^2}{S_2^2/\sigma_2^2}$$se distribuye como una variable F de Fisher-Snedecor con ($N_1$ y $N_2$) grados de libertad. En el caso del ANOVA, dado que dos de las condiciones son la normalidad de los grupos y la homocedasticidad de varianza ($\sigma_1^2$ = $\sigma_1^2$), el valor $F$ se puede obtener dividiendo las dos varianzas calculadas a partir de las muestras (intervariaza e intravarianza).
Existen diferentes tipos de ANOVA dependiendo de la si se trata de datos independientes (ANOVA entre sujetos), si son pareados (ANOVA de mediciones repetidas), si comparan la variable cuantitativa dependiente contra los niveles de una única variable cualitativa o factor (ANOVA de una vía) o frente a dos factores (ANOVA de dos vías). Este último puede ser a su vez aditivo o de interacción (los factores son independientes o no lo son). Cada uno de estos tipos de ANOVA tiene una serie de requerimientos propios.
En este documento se muestra cómo utilizar la librería Pingouin para realizar análisis ANOVA en python.
ANOVA de una vía para datos independientes¶
Definición¶
El ANOVA de una vía, también conocido como ANOVA con un factor o modelo factorial de un solo factor, permite estudiar si existen diferencias significativas entre la media de una variable aleatoria continua en los diferentes niveles de otra variable cualitativa o factor, cuando los datos no están pareados. Es una extensión de los t-test independientes para más de dos grupos.
Las hipótesis contrastadas en un ANOVA de un factor son:
$H_0$: No hay diferencias entre las medias de los diferentes grupos : $\mu_1 = \mu_2 ... = \mu_k = \mu$
$H_1$: Al menos un par de medias son significativamente distintas la una de la otra.
Otra forma de plantear las hipótesis de un ANOVA es la siguiente: si se considera $\mu$ como el valor esperado para una observación cualquiera de la población (la media de todas las observaciones sin tener en cuenta los diferentes niveles), y $\alpha_i$ el efecto introducido por el nivel $i$. La media de un determinado nivel ($\mu_i$) se puede definir como:
$$\mu_i = \mu + \alpha_i$$$H_0$: Ningún nivel introduce un efecto sobre la media total: $\alpha_1 = \alpha_2 =... \alpha_k = 0$
$H_1$: Al menos un nivel introduce un efecto que desplaza su media: Algún $\alpha_i \neq 0$
Como se ha mencionado anteriormente, la diferencia entre medias se detecta a través del estudio de la varianza entre grupos y dentro de grupos. Para lograrlo, el ANOVA requiere de una descomposición de la varianza basada en la siguiente idea:
$$\text{Variabilidad total =}$$$$\text{variabilidad debida a los diferentes niveles del factor + variabilidad residual}$$lo que es equivalente a:
$$\text{variabilidad explicada por el factor + variabilidad no explicada por el factor}$$lo que es equivalente a:
$$\text{(varianza entre niveles) + (varianza dentro de los niveles)}$$Para poder calcular las diferentes varianzas, en primer lugar se tienen que obtener la Sumas de Cuadrados (SS o Sc):
Suma de cuadrados total o total sum of squares (TSS): mide la variabilidad total de los datos, se define como la suma de los cuadrados de las diferencias de cada observación respecto a la media general de todas las observaciones. Los grados de libertad de la suma de cuadrados totales son igual al número total de observaciones menos uno (N-1).
Suma de cuadrados del factor o sum of squares due to treatment (SST): mide la variabilidad en los datos asociada al efecto del factor sobre la media (la diferencia de las medias entre los diferentes niveles o grupos). Se obtiene como la suma de los cuadrados de las desviaciones de la media de cada grupo respecto de la media general, ponderando cada diferencia al cuadrado por el número de observaciones de cada grupo. Los grados de libertad correspondientes son igual al número niveles del factor menos uno (k-1).
Suma de cuadrados residuales/error o sum of squares of errors (SSE): mide la variabilidad dentro de cada nivel, es decir, la variabilidad que no es debida a variable cualitativa. Se calcula como la suma de los cuadrados de las desviaciones de cada observación respecto a la media del nivel al que pertenece. Los grados de libertad asignados a la suma de cuadrados residuales equivalen a la diferencia entre los grados de libertad totales y los grados de libertad del factor, o lo que es lo mismo (N-k). En estadística se emplea el término error o residuo ya que se considera que esta es la variabilidad que muestran los datos debido a los errores de medida. Desde el punto de vista biológico tiene más sentido llamarlo suma de cuadrados dentro de grupos ya que se sabe que la variabilidad observada no solo se debe a errores de medida, si no a los muchos factores que no se controlan y que afectan a los procesos biológicos.
Una vez descompuesta la Suma de Cuadrados, se puede obtener la descomposición de la varianza dividiendo la Suma de Cuadrados entre los respectivos grados de libertad. De forma estricta, al cociente entre la Suma de Cuadrados y sus correspondientes grados de libertad se le denomina Cuadrados Medios o Mean Sum of Squares y pueden ser empleado como estimador de la varianza:
$\hat{S}_T^2 = \frac{TSS}{N-1} =$ Cuadrados Medios Totales = Cuasivarianza Total (varianza muestral total)
$\hat{S}_t^2 = \frac{SST}{k-1} =$ Cuadrados Medios del Factor = Intervarianza (varianza entre las medias de los distintos niveles)
$\hat{S}_E^2 = \frac{SSE}{N-k} =$ Cuadrados Medios del Error = Intravarianza (varianza dentro de los niveles, conocida como varianza residual o de error)
Nota: el ANOVA se define como análisis de varianza, pero en un sentido estricto, se trata de un análisis de la Suma de Cuadrados Medios.
Una vez descompuesta la estimación de la varianza, se obtiene el estadístico $F_{ratio}$ dividiendo la intervarianza entre la intravarianza:
$$F_{ratio} = \frac{Cuadrados \ Medios \ del \ Factor}{Cuadrados \ Medios \ del \ Error} = \frac{\hat{S}_t^2}{\hat{S}_E^2} = \frac{intervarianza}{intravarianza} \sim F_{k-1,N-k}$$Dado que por definición el estadístico $F_{ratio}$ sigue una distribución F Fisher-Snedecor con $k-1$ y $N-t$ grados de libertad, se puede conocer la probabilidad de obtener valores iguales o más extremos que los observados (p-values).
Condiciones para ANOVA de una vía con datos independientes¶
Las condiciones para ANOVA de una vía con datos independientes son:
Independencia: las observaciones deben ser aleatorias e independientes las unas de las otras. Los grupos (niveles del factor) deben de ser independientes entre ellos.
Distribución normal de cada uno de los niveles o grupos: la variable estudiada debe de distribuirse de forma normal en cada uno de los grupos, siendo menos estricta esta condición cuanto mayor sea el tamaño de cada grupo. La mejor forma de verificar la normalidad es estudiar los residuos de cada observación respecto a la media del grupo al que pertenecen.
A pesar de que el ANOVA es bastante robusto aun cuando existe cierta falta de normalidad, si la simetría es muy pronunciada y el tamaño de cada grupo no es muy grande, se puede recurrir en su lugar al test no paramétrico prueba H de Kruskal-Wallis. Con frecuencia se recomienda mantenerse con ANOVA a no ser que la falta de normalidad sea muy extrema.
Los datos atípicamente extremos pueden invalidar por completo las conclusiones de un ANOVA. Si se observan residuos extremos hay que estudiar con detalle a qué observaciones pertenecen, siendo aconsejable recalcular el ANOVA sin ellas y comparar los resultados obtenidos.
Misma varianza entre grupos (homocedasticidad): la varianza dentro de los grupos debe de ser aproximadamente igual en todos ellos. Esto es así ya que en la hipótesis nula se considera que todas las observaciones proceden de la misma población, por lo que tienen la misma media y también la misma varianza.
Esta condición es más importante cuanto menor es el tamaño de los grupos.
El ANOVA es bastante robusto a la falta de homodedasticidad si el diseño es equilibrado (mismo número de observaciones por grupo).
En diseños no equilibrados, la falta de homocedasticidad tiene mayor impacto. Si los grupos de menor tamaño son los que presentan mayor varianza, aumentará el número de falsos positivos. Si por el contrario, los grupos de mayor tamaño tienen mayor varianza aumentarán los falsos negativos.
Cuando no se puede aceptar la homocedasticidad, se puede recurrir a un ANOVA heterocedástico, que emplea la corrección de Welch (Welch test).
En el libro Handbook of Biological Statistics se considera altamente recomendable emplear diseños equilibrados. Siendo así, consideran fiable el ANOVA siempre y cuando el número de observaciones por grupo no sea menor de 10 y la desviación estándar no varíe más de 3 veces entre grupos. Para modelos no equilibrados recomiendan examinar con detalle la homocedasticidad, si las varianzas de los grupos no son muy semejantes es mejor emplear Welch's ANOVA.
Comparación múltiple de medias. Contrastes POST-HOC¶
Si un ANOVA resulta significativo implica que, al menos, dos de las medias comparadas son significativamente distintas entre sí, pero no se determina cuáles. Para identificarlas, hay que comparar dos a dos las medias de todos los grupos mediante un t-test u otro test que permita comparar 2 grupos.A esto se le conoce como análisis post-hoc. Debido a la inflación del error de tipo I, cuantas más comparaciones se hagan, más aumenta la probabilidad de encontrar diferencias significativas. Por ejemplo, para un nivel de significancia $\alpha$ = 0.05, de cada 100 comparaciones se esperan 5 significativas solo por azar.
Para evitar este problema, el nivel de significancia puede ajustarse en función del número de comparaciones (corrección de significancia). Si no se hace ningún tipo de corrección se aumenta la posibilidad de falsos positivos (error tipo I) pero, si se es muy estricto con las correcciones, se pueden considerar como no significativas diferencias que realmente sí lo son (error tipo II). La necesidad de corrección o no, y de qué tipo, se ha de estudiar con detenimiento en cada caso. A continuación, se describen los principales métodos de comparación post-hoc:
Intervalos LSD de Fisher (Least Significance Method)¶
Siendo $\overline{x}_i$ la media muestral de un grupo, la desviación típica estimada de dicha media (asumiendo la homocedasticidad de los grupos) es igual a la raíz cuadrada de los Cuadrados Medios del Error, que como se ha visto apartados anteriores, es la estimación de la intravarianza dividida por el número de observaciones de dicho grupo. Asumiendo también la normalidad de los grupos, se puede obtener el intervalo LSD como:
$$\overline{x}_i \pm \frac{\sqrt{2}}{2}t^{\alpha}_{gl(error)}\sqrt{\frac{SSE}{n}}$$Los intervalos LSD son básicamente un conjunto de t-test individuales con la única diferencia de que, en lugar de calcular una pooled SD empleando solo los dos grupos comparados, calcula la pooled SD a partir de todos los grupos disponibles.
Cuanto más se alejen los intervalos de dos grupos más diferentes son sus medias, siendo significativa dicha diferencia si los intervalos no se solapan. Es importante comprender que los intervalos LSD se emplean para comparar las medias pero no se pueden interpretar como un intervalo de confianza. El método LSD no conlleva ningún tipo de corrección de significancia, es por esto que su uso parece estar desaconsejado para determinar significancia aunque sí para identificar qué grupos tienen las medias más distantes.
Bonferroni adjustment¶
Este es posiblemente el ajuste de significancia más extendido a pesar de que no está recomendado para la mayoría de las situaciones que se dan en la práctica. La corrección de Bonferroni consiste en dividir el nivel de significancia $\alpha$ entre el número de comparaciones dos a dos realizadas.
$$\alpha_{corregido} = \frac{\alpha}{numero \ de \ grupos}$$Con esta corrección se asegura que la probabilidad de obtener al menos un falso positivo entre todas las comparaciones (family-wise error rate) es $\leq \alpha$. Permite contrastar una hipótesis nula general (la de que toda las hipótesis nulas testadas son verdaderas) de forma simultánea, cosa que raramente es de interés en las investigaciones. Se considera un método excesivamente conservativo, sobre todo a medida que se incrementa el número de comparaciones. Se desaconseja su utilización excepto en situaciones muy concretas. False discovery rate control is a recommended alternative to Bonferroni-type adjustments in health studies, Mark E. Glickman.
Holm–Bonferroni Adjustment¶
Con este método, el valor de significancia $\alpha$ se corrige secuencialmente haciéndolo menos conservativo que el de Bonferroni. Aun así, tampoco suele recomendarse si se realizan más de 6 comparaciones.
El proceso consiste en realizar un t-test para todas las comparaciones y ordenarlas de menor a mayor p-value. El nivel de significancia para la primera comparación (la que tiene menor p-value) se corrige dividiendo $\alpha$ entre el número total de comparaciones, si tras la corrección no resulta significativo, se detiene el proceso. Si sí que lo es, se corrige el nivel de significancia de la siguiente comparación (segundo menor p-value) dividiendo entre el número de comparaciones menos uno. El proceso se repite hasta detenerse cuando la comparación ya no sea significativa.
Tukey-Kramer Honest Significant Difference (HSD)¶
Es el ajuste recomendado cuando el número de grupos a comparar es mayor de 6 y el diseño es equilibrado (mismo número de observaciones por grupo). En el caso de modelos no equilibrados el método HSD es conservativo, requiere grandes diferencias para que resulte significativo.
El Tukey's test es muy similar a un t-test, excepto que corrige el experiment wise error rate. Esto lo consigue empleando un estadístico que sigue una distribución llamada studentized range distribution en lugar de una t-distribution. Este estadístico empleado se define como:
$$q_{calculado} = \frac{\overline{x}_{max}-\overline{x}_{min}}{S\sqrt{2/n}}$$donde $\overline{x}_{max}$ es la mayor de las medias de los dos grupos comparados, $\overline{x}_{min}$ la menor, S la pooled SD de estos dos grupos y n el número total de observaciones en los dos grupos.
Para cada par de grupos, se obtiene el valor $q_{calculado}$ y se compara con el esperado acorde a una studentized range distribution con los correspondientes grados de libertad. Si la probabilidad es menor al nivel de significancia $\alpha$ establecido, se considera significativa la diferencia de medias. Al igual que con los intervalos LSD, es posible calcular intervalos HSD para estudiar su solapamiento.
Dunnett’s correction (Dunnett’s test)¶
Es el equivalente al test Tukey-Kramer (HSD) recomendado cuando, en lugar de comparar todos los grupos entre sí ($\frac{(k-1)k}{2}$ comparaciones), solo se quieren comparar frente a un grupo control ($k-1$ comparaciones). Se emplea con frecuencia en experimentos médicos.
Inconvenientes de controlar el false positive rate mediante Bonferroni¶
Tal como se ha visto en los ejemplos, al realizar múltiples comparaciones es importante controlar la inflación del error de tipo I. Sin embargo, correcciones como las de Bonferroni o similares conllevan una serie de problemas.
El primer problema es que el método se desarrolló para contrastar la hipótesis nula universal de que los dos grupos son iguales para todas las variables testadas, no para aplicarlo de forma individual a cada test. A modo de ejemplo, supóngase que un investigador quiere determinar si un nuevo método de enseñanza es efectivo empleando para ello estudiantes de 20 colegios. En cada colegio se selecciona de forma aleatoria un grupo control y un grupo que se somete al nuevo método, y se realiza un test estadístico entre ambos considerando un nivel de significancia $\alpha = 0.05$. La corrección de Bonferroni implica comparar el p-value obtenido en los 20 test frente a 0.05/20 = 0.0025. Si alguno de los p-values es significativo, la conclusión de Bonferroni es que la hipótesis nula de que el nuevo sistema de enseñanza no es efectivo en todos los grupos (colegios) queda rechazada, por lo que se puede afirmar que el método de enseñanza es efectivo para alguno de los 20 grupos, pero no cuáles ni cuántos. Este tipo de información no es de interés en la gran mayoría de estudios, ya que lo que se desea conocer es qué grupos difieren.
El segundo problema de la corrección de Bonferroni es que una misma comparación es interpretada de forma distinta dependiendo del número de test que se hagan. Supóngase que un investigador realiza 20 contrastes de hipótesis y que todos ellos resultan en un p-value de 0.001. Aplicando la corrección de Bonferroni, si el límite de significancia para un test individual es de $\alpha=0.05$, el nivel de significancia corregido resulta ser 0.05/20 = 0.0025, por lo que el investigador concluye que todos los test son significativos. Un segundo investigador reproduce los mismos análisis en otro laboratorio y llega a los mismos resultados, pero para confirmarlos todavía más, realiza 80 test estadísticos adicionales. Esta vez, su nivel de significancia corregido pasa a ser de 0.05/100 = 0.0005. Ahora, ninguno de los test se puede considerar significativo, por lo que debido a aumentar el número de contrastes las conclusiones son totalmente contrarias.
Viendo los problemas que implica ¿Para qué sirve entonces la corrección de Bonferroni?
Que su aplicación en algunas disciplinas no sea adecuada no quita que pueda serlo en otras áreas. Imagínese una factoría que genera bombillas en lotes de 1000 unidades y que testar cada una de ellas antes de repartirlas no es factible. Una alternativa consiste en comprobar únicamente una muestra de cada lote, rechazando cualquier lote que tenga más de x bombillas defectuosas en la muestra. Por supuesto, la decisión puede ser errónea para un determinado lote, pero según la teoría de Neyman-Pearson, se puede encontrar el valor x para el que se minimiza el ratio de error. Ahora bien, la probabilidad de encontrar x bombillas defectuosas en la muestra depende del tamaño que tenga la muestra, o en otras palabras, del número de test que se hagan por lote. Si se incrementa el tamaño también lo hace la probabilidad de rechazar el lote, es aquí donde la corrección de Bonferroni recalcula el valor de x que mantiene minimizado el ratio de errores.
False Discovery Rate (FDR), Benjamini & Hochberg (BH)¶
Los métodos descritos anteriormente se centran en corregir la inflación del error de tipo I (false positive rate), es decir, la probabilidad de rechazar la hipótesis nula siendo esta cierta. Esta aproximación es útil cuando se emplea un número limitado de comparaciones. Para escenarios de large-scale multiple testing como los estudios genómicos, en los que se realizan miles de test de forma simultánea, el resultado de estos métodos es demasiado conservativo e impide que se detecten diferencias reales. Una alternativa es controlar el false discovery rate.
El false discovery rate (FDR) se define como: (todas las definiciones son equivalentes)
La proporción esperada de test en los que la hipótesis nula es cierta, de entre todos los test que se han considerado significativos.
FDR es la probabilidad de que una hipótesis nula sea cierta habiendo sido rechazada por el test estadístico.
De entre todos los test considerados significativos, el FDR es la proporción esperada de esos test para los que la hipótesis nula es verdadera.
Es la proporción de test significativos que realmente no lo son.
La proporción esperada de falsos positivos de entre todos los test considerados como significativos.
El objetivo de controlar el false discovery rate es establecer un límite de significancia para un conjunto de test tal que, de entre todos los test considerados como significativos, la proporción de hipótesis nulas verdaderas (falsos positivos) no supere un determinado valor. Otra ventaja añadida es su fácil interpretación, por ejemplo, si un estudio publica resultados estadísticamente significativos para un FDR del 10%, el lector tiene la seguridad de que como máximo un 10% de los resultados considerados como significativos son falsos positivos.
Cuando un investigador emplea un nivel de significancia $\alpha$, por ejemplo de 0.05, suele esperar cierta seguridad de que solo una pequeña fracción de los test significativos se corresponden con hipótesis nulas verdaderas (falsos positivos). Sin embargo, esto no tiene por qué ser así, ya que esto último depende de la frecuencia con la que la hipótesis nula contrastada es realmente verdadera. Un caso extremo sería aquel en el que todas las hipótesis nulas son realmente ciertas, en tal caso, el 100% de los test que en promedio resultan significativos son falsos positivos. Por lo tanto, la proporción de falsos positivos (false discovery rate) depende de la cantidad de hipótesis nulas que sean ciertas de entre todas los contrastes.
Los análisis de tipo exploratorio en los que el investigador trata de identificar resultados significativos sin apenas conocimiento previo se caracterizan por una proporción alta de hipótesis nulas falsas. Los análisis que se hacen para confirmar hipótesis, en los que el diseño se ha orientado en base a un conocimiento previo, suelen tener una proporción de hipótesis nulas verdaderas alta. Idealmente, si se conociera de antemano la proporción de hipótesis nulas verdaderas de entre todos los contrastes se podría ajustar con precisión el límite significancia adecuado a cada escenario, sin embargo, esto no ocurre en la realidad.
La primera aproximación para controlar el false discovery rate fue descrita por Benjamini y Hochberg en 1995. Acorde a su publicación, si se desea asegurar que en un estudio con n comparaciones el false discovery rate no supere un porcentaje d hay que:
Ordenar los n test de menor a mayor p-value ($p_1, \ p_2, \ ... \ p_n$)
Se define k como la última posición para la que se cumple que $p_i \leq d \frac{i}{n}$
Se consideran significativos todos los p-value hasta la posición k ($p_1, \ p_2, \ ... \ p_k$)
La principal ventaja de controlar el false discovery rate se hace más patente cuantas más comparaciones se realicen, por esta razón se suele emplear en situaciones con cientos o miles de comparaciones. Sin embargo, el método puede aplicarse también a estudios de menor envergadura.
El método propuesto por Benjamini & Hochberg asume, a la hora de estimar el número de hipótesis nulas erróneamente consideradas falsas, que todas las hipótesis nulas son ciertas. Como consecuencia, la estimación del FDR está inflada y por lo tanto es conservativa. Para información más detallada sobre comparaciones múltiples ver el documento: Comparaciones múltiples: corrección de p-value y FDR.
Tamaño del efecto $\eta^2$¶
El tamaño del efecto de un ANOVA, es el valor que permite medir cuanta varianza en la variable dependiente es resultado de la influencia de la variable cualitativa independiente, o lo que es lo mismo, cuánto afecta la variable independiente (factor) a la variable dependiente. En el ANOVA, la medida del tamaño del efecto más empleada es $\eta^2$ que se define como:
$$\eta^2= \frac{Suma Cuadrados_{entre \ grupos}}{Suma Cuadrados_{total}}$$Los niveles de clasificación más empleados para el tamaño del efecto son:
0.01 = pequeño
0.06 = mediano
0.14 = grande
Potencia (power) ANOVA de una vía¶
Los test de potencia permiten determinar la probabilidad de encontrar diferencias significativas entre las medias para un determinado $\alpha$ indicando el tamaño de los grupos, o bien calcular el tamaño que deben de tener los grupos para ser capaces de detectar con una determinada probabilidad una diferencia en las medias si esta existe. En aquellos casos que se quiere conocer el tamaño que han de tener las muestras, es necesario conocer (bien por experimentos previos o por muestras piloto) una estimación de la varianza de la población.
Resultados de un ANOVA¶
A la hora de comunicar los resultados de un ANOVA es conveniente indicar el valor obtenido para el estadístico $F$, los grados de libertad, el p-value y el tamaño del efecto ($\eta^2$).
Puede ocurrir que un análisis ANOVA indique que hay diferencias significativas entre las medias y luego que los t-test no encuentren ninguna comparación que lo sea. Esto no es contradictorio, simplemente es debido a que se trata de dos técnicas distintas.
Ejemplo¶
Supóngase que se un estudio quiere comprobar si existe una diferencia significativa entre el % de bateos exitosos de los jugadores de béisbol dependiendo de la posición en la que juegan. En el caso de que exista, se quiere saber qué posiciones difieren del resto.
Librerías¶
Las librerías utilizadas en este ejemplo son:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
plt.rcParams['lines.linewidth'] = 1.5
plt.rcParams['font.size'] = 8
import seaborn as sns
import pingouin as pg
from statsmodels.graphics.factorplots import interaction_plot
Datos¶
La siguiente tabla contiene una muestra de jugadores de la liga seleccionados aleatoriamente.
posicion = ["OF", "IF", "IF", "OF", "IF", "IF", "OF", "OF", "IF", "IF", "OF",
"OF", "IF", "OF", "IF", "IF", "IF", "OF", "IF", "OF", "IF", "OF",
"IF", "OF", "IF", "DH", "IF", "IF", "IF", "OF", "IF", "IF", "IF",
"IF", "OF", "IF", "OF", "IF", "IF", "IF", "IF", "OF", "OF", "IF",
"OF", "OF", "IF", "IF", "OF", "OF", "IF", "OF", "OF", "OF", "IF",
"DH", "OF", "OF", "OF", "IF", "IF", "IF", "IF", "OF", "IF", "IF",
"OF", "IF", "IF", "IF", "OF", "IF", "IF", "OF", "IF", "IF", "IF",
"IF", "IF", "IF", "OF", "DH", "OF", "OF", "IF", "IF", "IF", "OF",
"IF", "OF", "IF", "IF", "IF", "IF", "OF", "OF", "OF", "DH", "OF",
"IF", "IF", "OF", "OF", "C", "IF", "OF", "OF", "IF", "OF", "IF",
"IF", "IF", "OF", "C", "OF", "IF", "C", "OF", "IF", "DH", "C", "OF",
"OF", "IF", "C", "IF", "IF", "IF", "IF", "IF", "IF", "OF", "C", "IF",
"OF", "OF", "IF", "OF", "IF", "OF", "DH", "C", "IF", "OF", "IF",
"IF", "OF", "IF", "OF", "IF", "C", "IF", "IF", "OF", "IF", "IF",
"IF", "OF", "OF", "OF", "IF", "IF", "C", "IF", "C", "C", "OF", "OF",
"OF", "IF", "OF", "IF", "C", "DH", "DH", "C", "OF", "IF", "OF", "IF",
"IF", "IF", "C", "IF", "OF", "DH", "IF", "IF", "IF", "OF", "OF", "C",
"OF", "OF", "IF", "IF", "OF", "OF", "OF", "OF", "OF", "OF", "IF",
"IF", "DH", "OF", "IF", "IF", "OF", "IF", "IF", "IF", "IF", "OF",
"IF", "C", "IF", "IF", "C", "IF", "OF", "IF", "DH", "C", "OF", "C",
"IF", "IF", "OF", "C", "IF", "IF", "IF", "C", "C", "C", "OF", "OF",
"IF", "IF", "IF", "IF", "OF", "OF", "C", "IF", "IF", "OF", "C", "OF",
"OF", "OF", "OF", "OF", "OF", "OF", "OF", "OF", "OF", "OF", "C",
"IF", "DH", "IF", "C", "DH", "C", "IF", "C", "OF", "C", "C", "IF",
"OF", "IF", "IF", "IF", "IF", "IF", "IF", "IF", "IF", "OF", "OF",
"OF", "IF", "OF", "OF", "IF", "IF", "IF", "OF", "C", "IF", "IF",
"IF", "IF", "OF", "OF", "IF", "OF", "IF", "OF", "OF", "OF", "IF",
"OF", "OF", "IF", "OF", "IF", "C", "IF", "IF", "C", "DH", "OF", "IF",
"C", "C", "IF", "C", "IF", "OF", "C", "C", "OF"]
bateo = [0.359, 0.34, 0.33, 0.341, 0.366, 0.333, 0.37, 0.331, 0.381, 0.332,
0.365, 0.345, 0.313, 0.325, 0.327, 0.337, 0.336, 0.291, 0.34, 0.31,
0.365, 0.356, 0.35, 0.39, 0.388, 0.345, 0.27, 0.306, 0.393, 0.331,
0.365, 0.369, 0.342, 0.329, 0.376, 0.414, 0.327, 0.354, 0.321, 0.37,
0.313, 0.341, 0.325, 0.312, 0.346, 0.34, 0.401, 0.372, 0.352, 0.354,
0.341, 0.365, 0.333, 0.378, 0.385, 0.287, 0.303, 0.334, 0.359, 0.352,
0.321, 0.323, 0.302, 0.349, 0.32, 0.356, 0.34, 0.393, 0.288, 0.339,
0.388, 0.283, 0.311, 0.401, 0.353, 0.42, 0.393, 0.347, 0.424, 0.378,
0.346, 0.355, 0.322, 0.341, 0.306, 0.329, 0.271, 0.32, 0.308, 0.322,
0.388, 0.351, 0.341, 0.31, 0.393, 0.411, 0.323, 0.37, 0.364, 0.321,
0.351, 0.329, 0.327, 0.402, 0.32, 0.353, 0.319, 0.319, 0.343, 0.288,
0.32, 0.338, 0.322, 0.303, 0.356, 0.303, 0.351, 0.325, 0.325, 0.361,
0.375, 0.341, 0.383, 0.328, 0.3, 0.277, 0.359, 0.358, 0.381, 0.324,
0.293, 0.324, 0.329, 0.294, 0.32, 0.361, 0.347, 0.317, 0.316, 0.342,
0.368, 0.319, 0.317, 0.302, 0.321, 0.336, 0.347, 0.279, 0.309, 0.358,
0.318, 0.342, 0.299, 0.332, 0.349, 0.387, 0.335, 0.358, 0.312, 0.307,
0.28, 0.344, 0.314, 0.24, 0.331, 0.357, 0.346, 0.351, 0.293, 0.308,
0.374, 0.362, 0.294, 0.314, 0.374, 0.315, 0.324, 0.382, 0.353, 0.305,
0.338, 0.366, 0.357, 0.326, 0.332, 0.323, 0.306, 0.31, 0.31, 0.333,
0.34, 0.4, 0.389, 0.308, 0.411, 0.278, 0.326, 0.335, 0.316, 0.371,
0.314, 0.384, 0.379, 0.32, 0.395, 0.347, 0.307, 0.326, 0.316, 0.341,
0.308, 0.327, 0.337, 0.36, 0.32, 0.372, 0.306, 0.305, 0.347, 0.281,
0.281, 0.296, 0.306, 0.343, 0.378, 0.393, 0.337, 0.327, 0.336, 0.32,
0.381, 0.306, 0.358, 0.311, 0.284, 0.364, 0.315, 0.342, 0.367, 0.307,
0.351, 0.372, 0.304, 0.296, 0.332, 0.312, 0.437, 0.295, 0.316, 0.298,
0.302, 0.342, 0.364, 0.304, 0.295, 0.305, 0.359, 0.335, 0.338, 0.341,
0.3, 0.378, 0.412, 0.273, 0.308, 0.309, 0.263, 0.291, 0.359, 0.352,
0.262, 0.274, 0.334, 0.343, 0.267, 0.321, 0.3, 0.327, 0.313, 0.316,
0.337, 0.268, 0.342, 0.292, 0.39, 0.332, 0.315, 0.298, 0.298, 0.331,
0.361, 0.272, 0.287, 0.34, 0.317, 0.327, 0.354, 0.317, 0.311, 0.174,
0.302, 0.302, 0.291, 0.29, 0.268, 0.352, 0.341, 0.265, 0.307, 0.36,
0.305, 0.254, 0.279, 0.321, 0.305, 0.35, 0.308, 0.326, 0.219, 0.23,
0.322, 0.405, 0.321, 0.291, 0.312, 0.357, 0.324]
datos = pd.DataFrame({'posicion': posicion, 'bateo': bateo})
datos.head(4)
| posicion | bateo | |
|---|---|---|
| 0 | OF | 0.359 |
| 1 | IF | 0.340 |
| 2 | IF | 0.330 |
| 3 | OF | 0.341 |
Número de grupos, observaciones por grupo y distribución de las observaciones¶
Se identifica el número de grupos y cantidad de observaciones por grupo para determinar si es un modelo equilibrado. También se calculan la media y desviación típica de cada grupo.
# Número de observaciones por grupo
# ==============================================================================
datos.groupby('posicion').size()
posicion C 39 DH 14 IF 154 OF 120 dtype: int64
# Media y desviación típica por grupo
# ==============================================================================
datos.groupby('posicion').agg(['mean', 'std'])
| bateo | ||
|---|---|---|
| mean | std | |
| posicion | ||
| C | 0.322615 | 0.045132 |
| DH | 0.347786 | 0.036037 |
| IF | 0.331526 | 0.037095 |
| OF | 0.334250 | 0.029444 |
Dado que el número de observaciones por grupo no es constante, se trata de un modelo no equilibrado. Es importante tenerlo en cuenta cuando se comprueben las condiciones de normalidad y homocedasticidad.
Análisis gráfico¶
Dos de las representación más útiles antes de realizar un ANOVA son los gráficos Box-Plot y los Violin-Plot.
fig, ax = plt.subplots(1, 1, figsize=(8, 4))
sns.boxplot(x="posicion", y="bateo", data=datos, ax=ax)
sns.swarmplot(x="posicion", y="bateo", data=datos, color='black', alpha = 0.5, ax=ax);
Este tipo de representación permite identificar de forma preliminar si existen asimetrías, datos atípicos o diferencia de varianzas. En este caso, los 4 grupos parecen seguir una distribución simétrica. En el nivel IF se detectan algunos valores extremos que habrá que estudiar con detalle por si fuese necesario eliminarlos. El tamaño de las cajas es similar para todos los niveles por lo que no hay indicios de falta de homocedasticidad.
Verificar condiciones para un ANOVA¶
Independencia
Los grupos (variable categórica) y jugadores dentro de cada grupo son independientes entre ellos ya que se ha hecho un muestreo aleatorio de jugadores de toda la liga (no solo de un mismo equipo).
Distribución normal de las observaciones
La variable cuantitativa debe de distribuirse de forma normal en cada uno de los grupos. El estudio de normalidad puede hacerse de forma gráfica (qqplot) o con test de hipótesis.
# Gráficos qqplot
# ==============================================================================
fig, axs = plt.subplots(2, 2, figsize=(8, 7))
pg.qqplot(datos.loc[datos.posicion=='OF', 'bateo'], dist='norm', ax=axs[0,0])
axs[0,0].set_title('OF')
pg.qqplot(datos.loc[datos.posicion=='IF', 'bateo'], dist='norm', ax=axs[0,1])
axs[0,1].set_title('IF')
pg.qqplot(datos.loc[datos.posicion=='DH', 'bateo'], dist='norm', ax=axs[1,0])
axs[1,0].set_title('DH')
pg.qqplot(datos.loc[datos.posicion=='C', 'bateo'], dist='norm', ax=axs[1,1])
axs[1,1].set_title('C')
plt.tight_layout()
# Test de normalidad Shapiro-Wilk
# ==============================================================================
pg.normality(data=datos, dv='bateo', group='posicion')
| W | pval | normal | |
|---|---|---|---|
| posicion | |||
| OF | 0.993361 | 0.842244 | True |
| IF | 0.974849 | 0.006406 | False |
| DH | 0.972155 | 0.904090 | True |
| C | 0.980154 | 0.709178 | True |
Ni el análisis gráfico ni los test de hipótesis no muestran evidencias de falta de normalidad.
Varianza constante entre grupos (homocedasticidad)
Dado que hay un grupo IF que se encuentra en el límite para aceptar que se distribuye de forma normal, el test de Levene más adecuado que el de Bartlett.
# Test de homocedasticidad
# ==============================================================================
pg.homoscedasticity(data=datos, dv='bateo', group='posicion', method='levene')
| W | pval | equal_var | |
|---|---|---|---|
| levene | 2.605659 | 0.051799 | True |
Acorde al test Levene, no hay evidencias significativas que indiquen falta de homocedasticidad.
Test ANOVA¶
# Test ANOVA de una vía (One-way ANOVA)
# ==============================================================================
pg.anova(data=datos, dv='bateo', between='posicion', detailed=True)
| Source | SS | DF | MS | F | p-unc | np2 | |
|---|---|---|---|---|---|---|---|
| 0 | posicion | 0.007557 | 3 | 0.002519 | 1.994349 | 0.114693 | 0.018186 |
| 1 | Within | 0.407984 | 323 | 0.001263 | NaN | NaN | NaN |
Un p-value superior a 0.1 es una evidencia muy débil en contra de la hipótesis nula de que todos los grupos tienen la misma media. El valor de eta cuadrado ($\eta^2$) es de 0.018, lo que puede considerarse como un tamaño de efecto pequeño.
Comparaciones múltiples post-hoc¶
En este caso, el ANOVA no ha resultado significativo, por lo que no tiene sentido realizar comparaciones dos a dos. Sin embargo, con fines didácticos, se muestra como se obtienen los test TukeyHSD.
# Post-hoc Tukey test
# ==============================================================================
pg.pairwise_tukey(data=datos, dv='bateo', between='posicion').round(3)
| A | B | mean(A) | mean(B) | diff | se | T | p-tukey | hedges | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | C | DH | 0.323 | 0.348 | -0.025 | 0.011 | -2.273 | 0.106 | -0.577 |
| 1 | C | IF | 0.323 | 0.332 | -0.009 | 0.006 | -1.399 | 0.501 | -0.229 |
| 2 | C | OF | 0.323 | 0.334 | -0.012 | 0.007 | -1.776 | 0.287 | -0.341 |
| 3 | DH | IF | 0.348 | 0.332 | 0.016 | 0.010 | 1.639 | 0.358 | 0.437 |
| 4 | DH | OF | 0.348 | 0.334 | 0.014 | 0.010 | 1.349 | 0.533 | 0.446 |
| 5 | IF | OF | 0.332 | 0.334 | -0.003 | 0.004 | -0.629 | 0.923 | -0.080 |
Como era de esperar, no se encuentra diferencia significativa entre ningún par de medias.
Conclusión¶
En el estudio realizado se ha observado un tamaño de efecto pequeño y la técnicas de inferencia ANOVA no han encontrado significancia estadística para rechazar que las medias son iguales entre todos los grupos.
ANOVA de dos vías para datos independientes¶
Definición¶
El análisis de varianza de dos vías, también conocido como plan factorial con dos factores, sirve para estudiar la relación entre una variable dependiente cuantitativa y dos variables independientes cualitativas (factores), cada uno con varios niveles. El ANOVA de dos vías permite estudiar cómo influyen por si solos cada uno de los factores sobre la variable dependiente (modelo aditivo) así como la influencia de las combinaciones que se pueden dar entre ellas (modelo con interacción).
Supóngase que se quiere estudiar el efecto de un fármaco sobre la presión sanguínea (variable cuantitativa dependiente) dependiendo del sexo del paciente (niveles: hombre, mujer) y del tramo de edad (niveles: niño, adulto, anciano).
El efecto simple de los factores consiste en estudiar cómo varía el efecto del fármaco dependiendo del sexo sin diferenciar por edades, así como estudiar cómo varia el efecto del fármaco dependiendo de la edad sin tener en cuenta el sexo. El efecto de la interacción doble consiste en estudiar si la influencia de uno de los factores varía dependiendo de los niveles del otro factor. Es decir, si la influencia del factor sexo sobre la actividad del fármaco es distinta según la edad del paciente o, lo que es lo mismo, si la actividad del fármaco para una determinada edad es distinta según si se es hombre o mujer.
Condiciones para ANOVA de dos vías para datos independientes¶
Las condiciones necesarias para que un ANOVA de dos vías sea válido, así como el proceso a seguir para realizarlo son semejantes al ANOVA de una vía. Las únicas diferencias son:
Hipótesis: el ANOVA de dos vías con repeticiones combina 3 hipótesis nulas: que las medias de las observaciones agrupadas por un factor son iguales, que las medias de las observaciones agrupadas por el otro factor son iguales, y que no hay interacción entre los dos factores.
Requiere calcular la Suma de Cuadrados y Cuadrados Medios para ambos factores. Es frecuente encontrar que a un factor se le llama “tratamiento” y al otro bloque o block
Es importante tener en cuenta que, el orden en el que se multiplican los factores, no afecta al resultado del ANOVA únicamente si el tamaño de los grupos es igual (modelo equilibrado), de lo contrario sí importa. Por esta razón es recomendable que el diseño sea equilibrado.
Además, el estudio de la interacción de los dos factores solo es posible si se dispone varias observaciones para cada una de las combinaciones de los niveles.
Tamaño del efecto¶
En el caso del ANOVA con dos factores se puede calcular el tamaño del efecto eta cuadrado ($\eta^2$) para cada uno de los dos factores así como para la interacción.
Ejemplo 1¶
Una empresa de materiales de construcción quiere estudiar la influencia que tienen el grosor y el tipo de templado sobre la resistencia máxima de unas láminas de acero. Para ello miden el estrés hasta la rotura (variable cuantitativa dependiente) para dos tipos de templado (lento y rápido) y tres grosores de lámina (8mm, 16mm y 24 mm).
Nota: con el objetivo de simplificar el ejemplo, se asume que se cumplen las condiciones para un ANOVA de dos vías. En un caso real, siempre hay que validar las condiciones sobre las que se apoya un método o técnica.
Librerías¶
Las librerías utilizadas en este ejemplo son:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pingouin as pg
Datos¶
resistencia = [15.29, 15.89, 16.02, 16.56, 15.46, 16.91, 16.99, 17.27, 16.85,
16.35, 17.23, 17.81, 17.74, 18.02, 18.37, 12.07, 12.42, 12.73,
13.02, 12.05, 12.92, 13.01, 12.21, 13.49, 14.01, 13.30, 12.82,
12.49, 13.55, 14.53]
templado = ["rapido"] * 15 + ["lento"] * 15
grosor = ([8] * 5 + [16] * 5 + [24] * 5) * 2
datos = pd.DataFrame({
'templado': templado,
'grosor': grosor,
'resistencia': resistencia
})
datos.head()
| templado | grosor | resistencia | |
|---|---|---|---|
| 0 | rapido | 8 | 15.29 |
| 1 | rapido | 8 | 15.89 |
| 2 | rapido | 8 | 16.02 |
| 3 | rapido | 8 | 16.56 |
| 4 | rapido | 8 | 15.46 |
Análisis descriptivo y gráfico¶
En primer lugar, se generan los diagramas Box-plot para identificar posibles diferencias notables, asimetrías, valores atípicos y homogeneidad de varianza entre los distintos niveles. Se calcula también la media y varianza de cada grupo.
fig, axs = plt.subplots(1, 2, figsize=(10, 4))
axs[0].set_title('Resistencia vs templado')
sns.boxplot(x="templado", y="resistencia", data=datos, ax=axs[0])
sns.swarmplot(x="templado", y="resistencia", data=datos, color='black',
alpha = 0.5, ax=axs[0])
axs[1].set_title('Resistencia vs grosor')
sns.boxplot(x="grosor", y="resistencia", data=datos, ax=axs[1])
sns.swarmplot(x="grosor", y="resistencia", data=datos, color='black',
alpha = 0.5, ax=axs[1]);
fig, ax = plt.subplots(1, 1, figsize=(8, 4))
ax.set_title('Resistencia vs templado y grosor')
sns.boxplot(x="templado", y="resistencia", hue='grosor', data=datos, ax=ax);
print('Resistencia media y desviación típica por templado')
datos.groupby('templado')['resistencia'].agg(['mean', 'std'])
Resistencia media y desviación típica por templado
| mean | std | |
|---|---|---|
| templado | ||
| lento | 12.974667 | 0.711345 |
| rapido | 16.850667 | 0.927643 |
print('Resistencia media y desviación típica por grosor')
datos.groupby('grosor')['resistencia'].agg(['mean', 'std'])
Resistencia media y desviación típica por grosor
| mean | std | |
|---|---|---|
| grosor | ||
| 8 | 14.151 | 1.836993 |
| 16 | 15.001 | 2.036797 |
| 24 | 15.586 | 2.442354 |
print('Resistencia media y desviación típica por templado y grosor')
datos.groupby(['templado', 'grosor'])['resistencia'].agg(['mean', 'std'])
Resistencia media y desviación típica por templado y grosor
| mean | std | ||
|---|---|---|---|
| templado | grosor | ||
| lento | 8 | 12.458 | 0.420797 |
| 16 | 13.128 | 0.672473 | |
| 24 | 13.338 | 0.783371 | |
| rapido | 8 | 15.844 | 0.500030 |
| 16 | 16.874 | 0.334186 | |
| 24 | 17.834 | 0.417169 |
A partir de la representación gráfica y el cálculo de las medias se puede intuir que existe una diferencia en la resistencia alcanzada dependiendo del tipo de templado. La resistencia parece incrementarse a medida que aumenta el grosor de la lámina, si bien no está claro que la diferencia en las medias sea significativa. La distribución de las observaciones de cada nivel parece simétrica sin presencia de valores atípicos. A priori, parece que se satisfacen las condiciones necesarias para un ANOVA.
Otra forma de identificar de forma gráfica posibles interacciones entre los dos factores es mediante lo que se conocen como “gráficos de interacción”. Si las líneas que describen los datos para cada uno de los niveles son paralelas, significa que el comportamiento es similar independientemente del nivel del factor, es decir, no hay interacción.
fig, ax = plt.subplots(figsize=(6, 4))
fig = interaction_plot(
x = datos.templado,
trace = datos.grosor,
response = datos.resistencia,
ax = ax,
)
fig, ax = plt.subplots(figsize=(6, 4))
fig = interaction_plot(
x = datos.grosor,
trace = datos.templado,
response = datos.resistencia,
ax = ax,
)
El primer gráfico de interacción parece indicar que el incremento de resistencia entre los dos tipos de templado es proporcional para los tres grosores. En el segundo gráfico, se observa cierta desviación en el grosor de 24mm. Esto podría deberse a simple variabilidad o porque existe interacción entre las variables grosor y templado. Estos indicios serán confirmados o descartados mediante el ANOVA.
Test ANOVA¶
# Test ANOVA de dos vías (Two-way ANOVA)
# ==============================================================================
pg.anova(
data = datos,
dv = 'resistencia',
between = ['templado', 'grosor'],
detailed = True
).round(4)
| Source | SS | DF | MS | F | p-unc | np2 | |
|---|---|---|---|---|---|---|---|
| 0 | templado | 112.6753 | 1 | 112.6753 | 380.0820 | 0.0000 | 0.9406 |
| 1 | grosor | 10.4132 | 2 | 5.2066 | 17.5631 | 0.0000 | 0.5941 |
| 2 | templado * grosor | 1.6035 | 2 | 0.8018 | 2.7045 | 0.0873 | 0.1839 |
| 3 | Residual | 7.1148 | 24 | 0.2964 | NaN | NaN | NaN |
El análisis de varianza confirma que existe una influencia significativa sobre la resistencia de las láminas por parte de ambos factores (templado y grosor) con tamaños de efecto $\eta^2$ grande y mediano respectivamente. Sin embargo, no se detecta una interacción significativa entre ellos.
Ejemplo 2¶
Supóngase un estudio clínico que analiza la eficacia de un medicamento teniendo en cuenta dos factores, el sexo (masculino y femenino) y la juventud (joven, adulto). Se quiere analizar si el efecto es diferente entre alguno de los niveles de cada variable por sí sola o en combinación.
Este estudio implica comprobar si el efecto medio del fármaco es significativamente distinto entre alguno de los siguientes grupos: hombres, mujeres, jóvenes, adultos, hombres jóvenes, hombres adultos, mujeres jóvenes y mujeres adultas.
Librerías¶
Las librerías utilizadas en este ejemplo son:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pingouin as pg
Datos¶
subject = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30]
sex = ["female", "male", "male", "female", "male", "male", "male", "female",
"female", "male", "male", "male", "male", "female", "female", "female",
"male", "female", "female", "male", "male", "female", "male", "male",
"male", "male", "male", "male", "female", "male"]
age = ["adult", "adult", "adult", "adult", "adult", "adult", "young", "young",
"adult", "young", "young", "adult", "young", "young", "young", "adult",
"young", "adult", "young", "young", "young", "young", "adult", "young",
"young", "young", "young", "young", "young", "adult"]
result = [7.1, 11.0, 5.8, 8.8, 8.6, 8.0, 3.0, 5.2, 3.4, 4.0, 5.3, 11.3, 4.6, 6.4,
13.5, 4.7, 5.1, 7.3, 9.5, 5.4, 3.7, 6.2, 10.0, 1.7, 2.9, 3.2, 4.7, 4.9,
9.8, 9.4]
datos = pd.DataFrame({
'subject': subject,
'sex': sex,
'age': age,
'result': result
})
datos.head()
| subject | sex | age | result | |
|---|---|---|---|---|
| 0 | 1 | female | adult | 7.1 |
| 1 | 2 | male | adult | 11.0 |
| 2 | 3 | male | adult | 5.8 |
| 3 | 4 | female | adult | 8.8 |
| 4 | 5 | male | adult | 8.6 |
Análisis descriptivo y gráfico¶
En primer lugar, se generan los diagramas Box-plot para identificar posibles diferencias notables, asimetrías, valores atípicos y homogeneidad de varianza entre los distintos niveles. Se calcula también la media y varianza de cada grupo.
fig, axs = plt.subplots(1, 2, figsize=(10, 4))
axs[0].set_title('Resultados vs edad')
sns.boxplot(x="age", y="result", data=datos, ax=axs[0])
sns.swarmplot(x="age", y="result", data=datos, color='black',
alpha = 0.5, ax=axs[0])
axs[1].set_title('Resultados vs sexo')
sns.boxplot(x="sex", y="result", data=datos, ax=axs[1])
sns.swarmplot(x="sex", y="result", data=datos, color='black',
alpha = 0.5, ax=axs[1]);
fig, ax = plt.subplots(1, 1, figsize=(8, 4))
ax.set_title('Resultados vs sexo y edad')
sns.boxplot(x="age", y="result", hue='sex', data=datos, ax=ax);
print('Resultados medios y desviación típica por edad')
datos.groupby('age')['result'].agg(['mean', 'std'])
Resultados medios y desviación típica por edad
| mean | std | |
|---|---|---|
| age | ||
| adult | 7.950000 | 2.431049 |
| young | 5.505556 | 2.871047 |
print('Resultados medios y desviación típica por sexo')
datos.groupby('sex')['result'].agg(['mean', 'std'])
Resultados medios y desviación típica por sexo
| mean | std | |
|---|---|---|
| sex | ||
| female | 7.445455 | 2.828202 |
| male | 5.926316 | 2.906858 |
print('Resultados medios y desviación típica por edad y sexo')
datos.groupby(['age', 'sex'])['result'].agg(['mean', 'std'])
Resultados medios y desviación típica por edad y sexo
| mean | std | ||
|---|---|---|---|
| age | sex | ||
| adult | female | 6.260000 | 2.170944 |
| male | 9.157143 | 1.900752 | |
| young | female | 8.433333 | 3.106552 |
| male | 4.041667 | 1.157158 |
A partir de la representación gráfica y el cálculo de las medias se puede intuir que existe una diferencia en el efecto del fármaco dependiendo de la edad y también del sexo. El efecto parece ser mayor en mujeres que en hombres y en adultos que en jóvenes, si bien la significancia se tendrá que confirmar con el ANOVA. La distribución de las observaciones de cada nivel parece simétrica con la presencia de un único valor atípico. A priori parece que se satisfacen las condiciones necesarias para un ANOVA, aunque habrá que confirmarlas estudiando los residuos.
# Gráfico de interacciones
# ==============================================================================
fig, ax = plt.subplots(figsize=(6, 4))
fig = interaction_plot(
x = datos.age,
trace = datos.sex,
response = datos.result,
ax = ax,
)
Se observa una clara interacción entre ambos factores. La respuesta al fármaco es distinta entre adultos y jóvenes, y de tendencia inversa dependiendo del sexo. En mujeres, la respuesta es mayor cuando son jóvenes que cuando son adultas y en hombres mayor cuando son adultos y menor cuando son jóvenes. El ANOVA confirmará si las diferencias observadas son significativas.
Test ANOVA¶
# Test ANOVA de dos vías (Two-way ANOVA)
# ==============================================================================
pg.anova(
data = datos,
dv = 'result',
between = ['sex', 'age'],
detailed = True
).round(4)
| Source | SS | DF | MS | F | p-unc | np2 | |
|---|---|---|---|---|---|---|---|
| 0 | sex | 12.0164 | 1.0 | 12.0164 | 3.0183 | 0.0942 | 0.1040 |
| 1 | age | 38.9611 | 1.0 | 38.9611 | 9.7862 | 0.0043 | 0.2735 |
| 2 | sex * age | 89.6114 | 1.0 | 89.6114 | 22.5085 | 0.0001 | 0.4640 |
| 3 | Residual | 103.5116 | 26.0 | 3.9812 | NaN | NaN | NaN |
El análisis de varianza no encuentra diferencias significativas en el efecto del fármaco entre hombres y mujeres (factor sex) pero sí encuentra diferencias significativas entre jóvenes y adultos y entre al menos dos grupos de las combinaciones de sexo y edad, es decir, hay significancia para la interacción. El tamaño del efecto $\eta^2$ es grande tanto para edad como para la interacción de edad y sexo.
Nota: en este caso, el orden en el que se multiplican los factores sí afecta a los resultados puesto que el tamaño de los grupos no es igual.
ANOVA con variables dependientes (ANOVA de medidas repetidas)¶
Cuando las variables a comparar son mediciones distintas pero sobre los mismos sujetos, no se cumple la condición de independencia, por lo que se requiere un ANOVA específico que realice comparaciones considerando que los datos son pareados (de forma similar como se hace en los t-test pareados pero para comparar más de dos grupos).
Condiciones para ANOVA de variables dependientes¶
Esfericidad
Es la única condición para poder aplicar este tipo de análisis. La esfericidad implica que la varianza de las diferencias entre todos los pares de variables a comparar es igual. Si el ANOVA se realiza para comparar la media de una variable cuantitativa entre tres niveles (A, B, C), se aceptará la esfericidad si la varianza de las diferencias entre A-B, A-C, B-C es la misma.
La esfericidad se puede analizar mediante el test de Mauchly cuya hipótesis nula es que sí existe esfericidad. En la práctica, es frecuente que la condición de esfericidad no se cumpla, en tal caso, se pueden aplicar a los p-values las correcciones de Greenhouse-Geisser y la de Huynh-Feldt. Otra alternativa, en caso de no cumplirse la esfericidad, es el test no paramétrico Friedman.
La función rm_anova de la librería pingouin, si se indica el argumento correction = True, aplica automáticamente el test de esfericidad de Mauchly, si encuentra evidencias de que no se cumple la condición, corrige los p-values con el método de Greenhouse-Geisser.
Ejemplo¶
Supóngase un estudio en el que se quiere comprobar si el precio de la compra varía entre 4 cadenas de supermercado. Para ello, se selecciona una serie de elementos de la compra cotidiana y se registra su valor en cada uno de los supermercados ¿Existen evidencias de que el precio medio de la compra es diferente dependiendo del supermercado?
Se trata de distintas mediciones sobre un mismo elemento por lo tanto, son datos pareados.
Librerías¶
Las librerías utilizadas en este ejemplo son:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pingouin as pg
from statsmodels.graphics.factorplots import interaction_plot
Datos¶
producto = ["lettuce", "potatoes", "milk", "eggs", "bread", "cereal", "ground.beef",
"tomato.soup", "laundry.detergent", "aspirin"]
tienda_A = [1.755, 2.655, 2.235, 0.975, 2.370, 4.695, 3.135, 0.930, 8.235, 6.690]
tienda_B = [1.78, 1.98, 1.69, 0.99, 1.70, 3.15, 1.88, 0.65, 5.99, 4.84]
tienda_C = [1.29, 1.99, 1.79, 0.69, 1.89, 2.99, 2.09, 0.65, 5.99, 4.99]
tienda_D = [1.29, 1.99, 1.59, 1.09, 1.89, 3.09, 2.49, 0.69, 6.99, 5.15]
datos = pd.DataFrame({
'producto':producto * 4,
'tienda': np.repeat(['A', 'B', 'C', 'D'], 10),
'precio': tienda_A + tienda_B + tienda_C + tienda_D
})
datos.head()
| producto | tienda | precio | |
|---|---|---|---|
| 0 | lettuce | A | 1.755 |
| 1 | potatoes | A | 2.655 |
| 2 | milk | A | 2.235 |
| 3 | eggs | A | 0.975 |
| 4 | bread | A | 2.370 |
Análisis descriptivo y gráfico¶
fig, ax = plt.subplots(1, 1, figsize=(8, 4))
ax.set_title('Precios vs tienda')
sns.boxplot(x="tienda", y="precio", data=datos, ax=ax)
sns.swarmplot(x="tienda", y="precio", data=datos, color='black', alpha=0.5, ax=ax);
print('Precios medios y desviación típica por tienda')
datos.groupby('tienda')['precio'].agg(['mean', 'std'])
Precios medios y desviación típica por tienda
| mean | std | |
|---|---|---|
| tienda | ||
| A | 3.3675 | 2.440371 |
| B | 2.4650 | 1.707430 |
| C | 2.4360 | 1.765296 |
| D | 2.6260 | 1.987758 |
Test ANOVA¶
# Test ANOVA de dos vías (Two-way ANOVA)
# ==============================================================================
pg.rm_anova(
data = datos,
dv = 'precio',
within = 'tienda',
subject = 'producto',
detailed = True,
correction = 'auto'
).round(4)
| Source | SS | DF | MS | F | p-unc | p-GG-corr | ng2 | eps | sphericity | W-spher | p-spher | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | tienda | 5.7372 | 3 | 1.9124 | 13.0252 | 0.0 | 0.0017 | 0.0385 | 0.4682 | False | 0.129 | 0.0079 |
| 1 | Error | 3.9642 | 27 | 0.1468 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
Dado que la esfericidad no se cumple (sphericity = False), hay que utilizar el p-value corregido, que está en la columna p-GG-corr. El análisis de varianza muestra evidencias significativas con un tamaño de efecto grande.
Comparaciones múltiples¶
Al tratarse de datos pareados, no se pueden calcular los intervalos Tukey HSD. En su lugar, se pueden utilizar t-test pareados.
# Post-hoc pairwise t-test
# ==============================================================================
pg.pairwise_tests(
dv = 'precio',
within = 'tienda',
subject = 'producto',
padjust = 'holm',
data = datos
)
| Contrast | A | B | Paired | Parametric | T | dof | alternative | p-unc | p-corr | p-adjust | BF10 | hedges | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | tienda | A | B | True | True | 3.630938 | 9.0 | two-sided | 0.005478 | 0.021910 | holm | 10.073 | 0.410424 |
| 1 | tienda | A | C | True | True | 4.166418 | 9.0 | two-sided | 0.002424 | 0.013625 | holm | 19.615 | 0.418894 |
| 2 | tienda | A | D | True | True | 4.210567 | 9.0 | two-sided | 0.002271 | 0.013625 | holm | 20.701 | 0.319091 |
| 3 | tienda | B | C | True | True | 0.405600 | 9.0 | two-sided | 0.694510 | 0.694510 | holm | 0.331 | 0.015994 |
| 4 | tienda | B | D | True | True | -1.242763 | 9.0 | two-sided | 0.245358 | 0.490715 | holm | 0.571 | -0.083219 |
| 5 | tienda | C | D | True | True | -1.770733 | 9.0 | two-sided | 0.110379 | 0.331137 | holm | 0.983 | -0.096803 |
Conclusión¶
El análisis ANOVA (incluyendo las correcciones dada la falta de esfericidad) encuentra diferencias significativas en el precio de los alimentos entre al menos 2 tiendas, siendo el tamaño del efecto grande. La posterior comparación dos a dos por t-student con corrección de significancia holm identifica como significativas las diferencias entre las tiendas A-B, A-C y A-D pero no entre B-C, B-D y C-D.
Información de sesión¶
import session_info
session_info.show(html=False)
----- matplotlib 3.10.7 numpy 2.2.6 pandas 2.3.3 pingouin 0.5.5 seaborn 0.13.2 session_info v1.0.1 statsmodels 0.14.5 ----- IPython 9.6.0 jupyter_client 7.4.9 jupyter_core 5.9.1 notebook 6.5.7 ----- Python 3.13.9 | packaged by Anaconda, Inc. | (main, Oct 21 2025, 19:16:10) [GCC 11.2.0] Linux-6.14.0-35-generic-x86_64-with-glibc2.39 ----- Session information updated at 2025-11-19 23:27
Bibliografía¶
OpenIntro Statistics: Fourth Edition by David Diez, Mine Çetinkaya-Rundel, Christopher Barr libro
Statistics Using R with Biological Examples by Kim Seefeld, Ernst Linder
Handbook of Biological Statistics by John H. McDonald
Métodos estadísticos en ingeniería Rafael Romero Villafranca, Luisa Rosa Zúnica Ramajo
Instrucciones para citar¶
¿Cómo citar este documento?
Si utilizas este documento o alguna parte de él, te agradecemos que lo cites. ¡Muchas gracias!
Análisis de Varianza (ANOVA) con Python por Joaquín Amat Rodrigo, disponible bajo una licencia Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0 DEED) en https://www.cienciadedatos.net/documentos/pystats09-analisis-de-varianza-anova-python.html
¿Te ha gustado el artículo? Tu ayuda es importante
Tu contribución me ayudará a seguir generando contenido divulgativo gratuito. ¡Muchísimas gracias! 😊
Este documento creado por Joaquín Amat Rodrigo tiene licencia Attribution-NonCommercial-ShareAlike 4.0 International.
Se permite:
-
Compartir: copiar y redistribuir el material en cualquier medio o formato.
-
Adaptar: remezclar, transformar y crear a partir del material.
Bajo los siguientes términos:
-
Atribución: Debes otorgar el crédito adecuado, proporcionar un enlace a la licencia e indicar si se realizaron cambios. Puedes hacerlo de cualquier manera razonable, pero no de una forma que sugiera que el licenciante te respalda o respalda tu uso.
-
No-Comercial: No puedes utilizar el material para fines comerciales.
-
Compartir-Igual: Si remezclas, transformas o creas a partir del material, debes distribuir tus contribuciones bajo la misma licencia que el original.

