Si te gusta Skforecast , ayúdanos dándonos una estrella en GitHub! ⭐️
Predicción (forecasting) visitas página web con machine learning
Más sobre forecasting
- Forecasting series temporales con Python y Scikit Learn
- Predicción (forecasting) de la demanda eléctrica con Python
- Forecasting series temporales con gradient boosting: Skforecast, XGBoost, LightGBM y CatBoost
- Predicción del precio de Bitcoin con Python
- Intervalos de predicción en modelos de forecasting
- Multi-series forecasting
- Predicción de demanda intermitente
Introducción¶
Una serie temporal (time series) es una sucesión de datos ordenados cronológicamente, espaciados a intervalos iguales o desiguales. El proceso de forecasting consiste en predecir el valor futuro de una serie temporal, bien modelando la serie únicamente en función de su comportamiento pasado (autorregresivo) o empleando otras variables externas.
En este documento se muestra un ejemplo de cómo utilizar métodos machine learning y modelado estadístico (ARIMA) para predecir el número de visitas diarias que recibe una página web. Para ello, se hace uso de skforecast, una sencilla librería de Python que permite, entre otras cosas, adaptar cualquier regresor de scikit-learn a problemas de forecasting.
Caso de uso¶
Se dispone del historial de visitas diarias a la web cienciadedatos.net desde el 01/07/2020. Se pretende generar un modelo de forecasting capaz de predecir el tráfico web que tendrá la página a 7 días vista. En concreto, el usuario quiere ser capaz de ejecutar el modelo cada lunes y obtener las predicciones de tráfico diario hasta el lunes siguiente.
Con el objetivo de poder evaluar de forma robusta la capacidad del modelo acorde al uso que se le quiere dar, conviene no limitarse a predecir únicamente los últimos 7 días de la serie temporal, sino simular el proceso completo. El backtesting es un tipo especial de cross-validation que se aplica al periodo o periodos anteriores y puede emplearse con diferentes estrategias:
Backtesting con reentrenamiento (refit)
El modelo se entrena cada vez antes de realizar las predicciones, de esta forma, se incorpora toda la información disponible hasta el momento. Se trata de una adaptación del proceso de cross-validation en el que, en lugar de hacer un reparto aleatorio de las observaciones, el conjunto de entrenamiento se incrementa de manera secuencial, manteniendo el orden temporal de los datos.
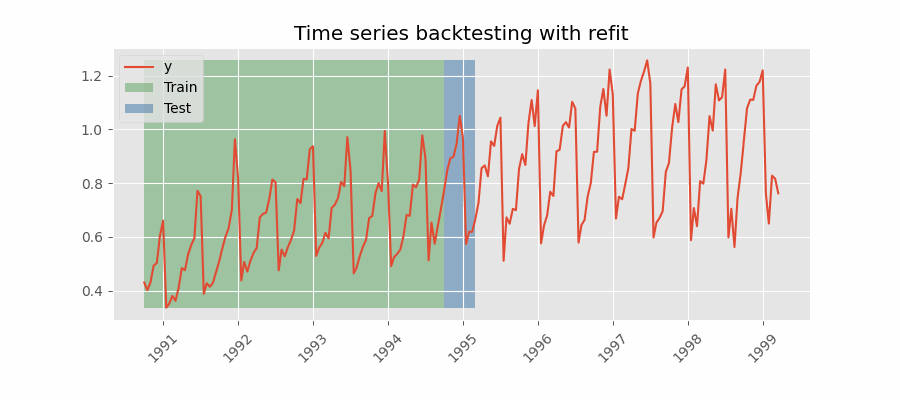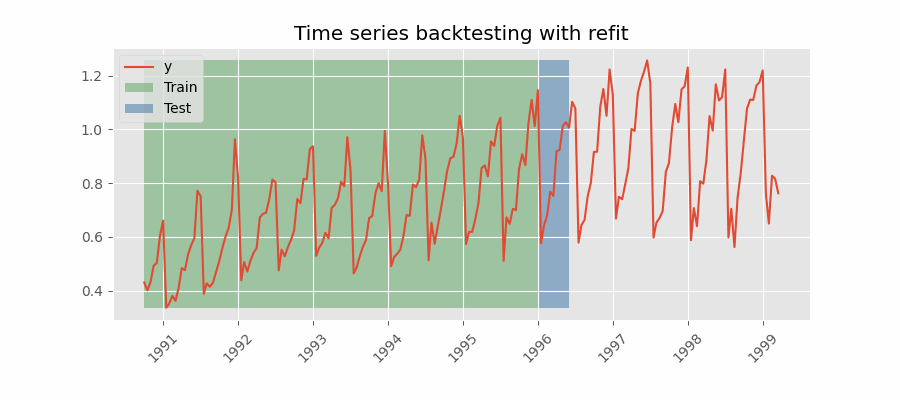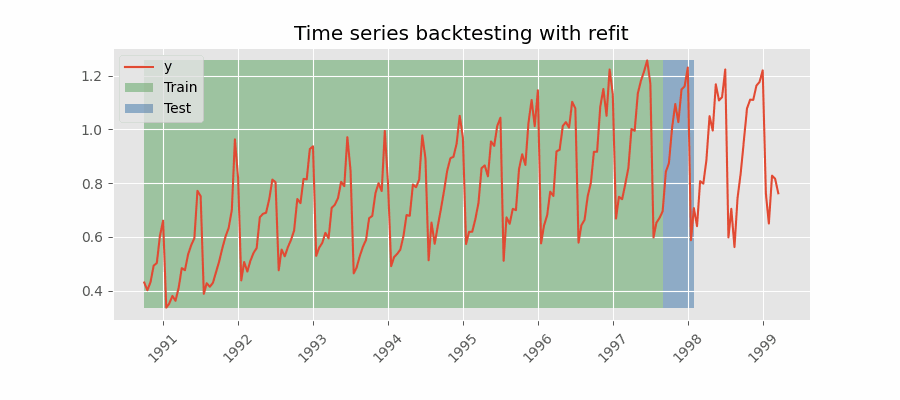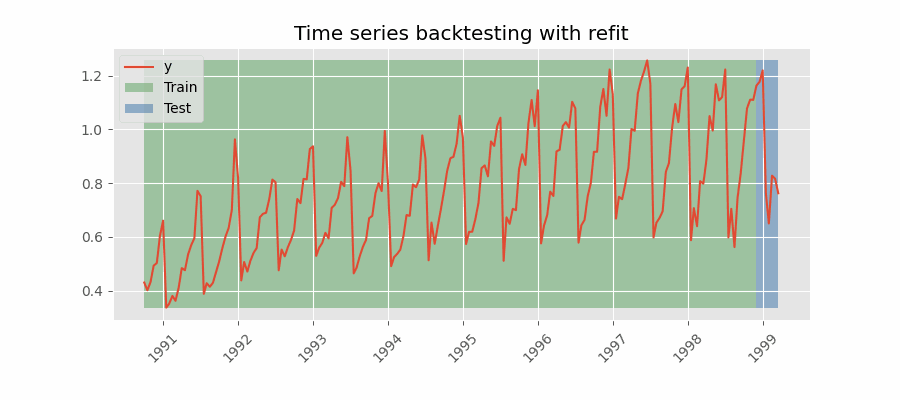
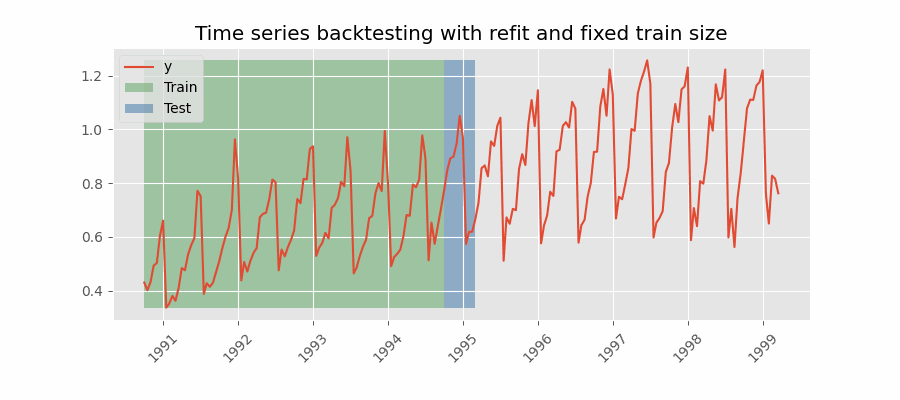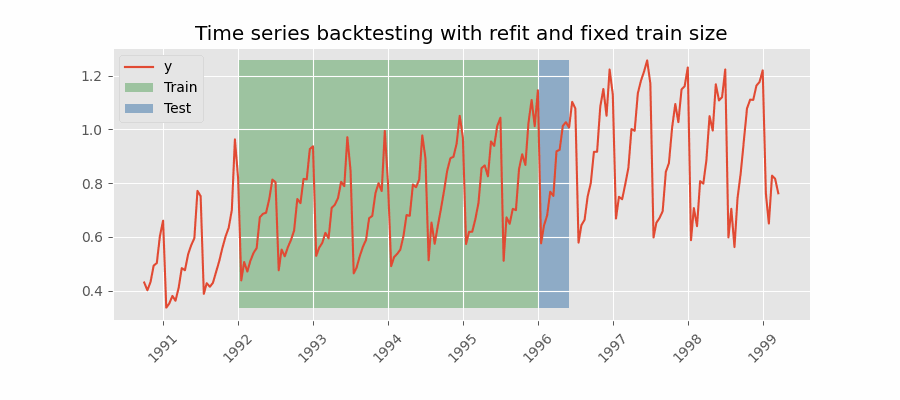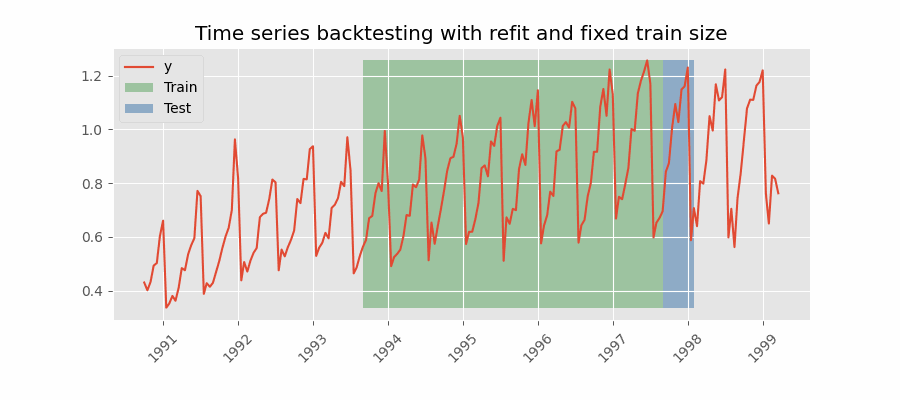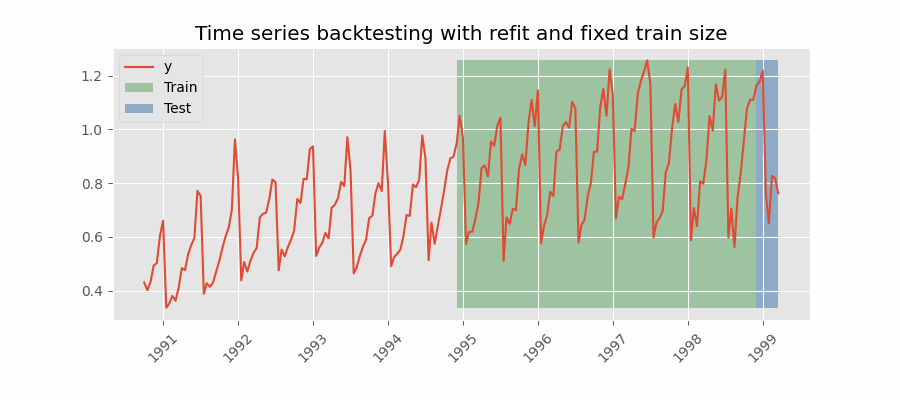
Backtesting con reentrenamiento y tamaño de entrenamiento constante (rolling origin)
Similar a la estrategia anterior, pero, en este caso, el tamaño del conjunto de entrenamiento no se incrementa sino que la ventana de tiempo que abarca se desplaza. Esta estrategia se conoce también como time series cross-validation o walk-forward validation.
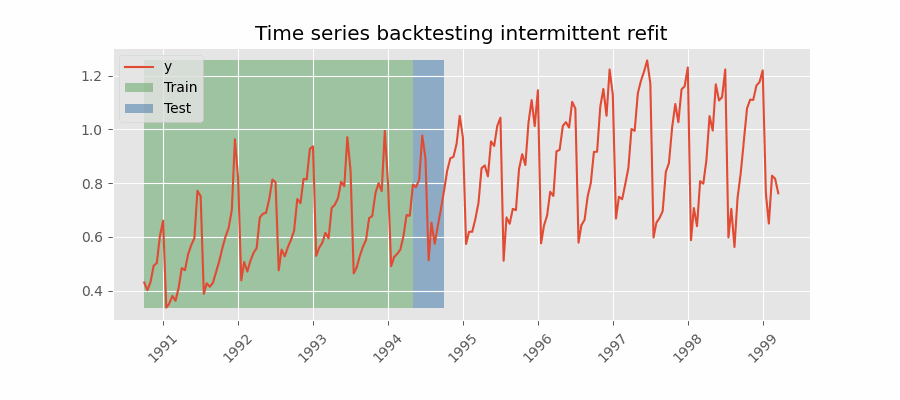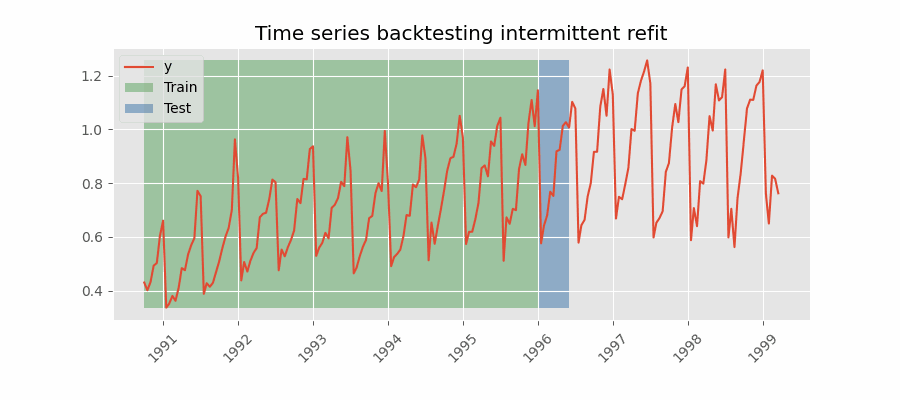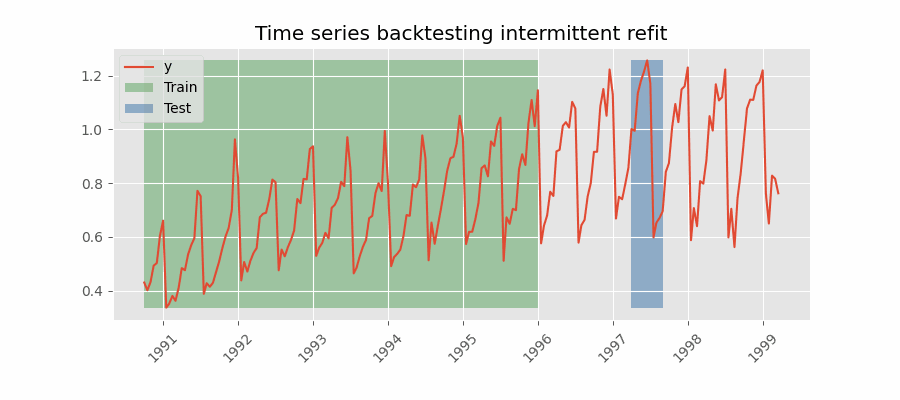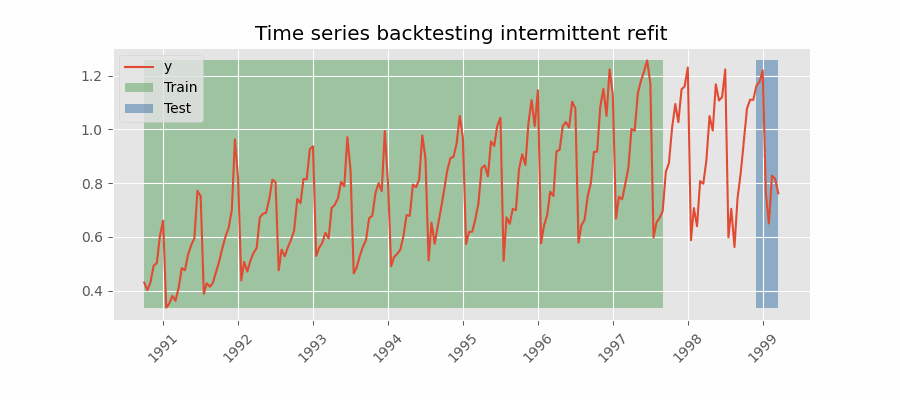
Backtesting con reentrenamiento cada n periodos (intermitente)
El modelo se reentrena de forma intermitente cada $n$ periodos de predicción.
Backtesting sin reentrenamiento
Con esta estrategia, el modelo se entrena una única vez con un conjunto inicial y se realizan las predicciones de forma secuencial sin actualizar el modelo y siguiendo el orden temporal de los datos. Esta estrategia tiene la ventaja de ser mucho más rápida puesto que el modelo solo se entrena una vez. La desventaja es que el modelo no incorpora la última información disponible por lo que puede perder capacidad predictiva con el tiempo.
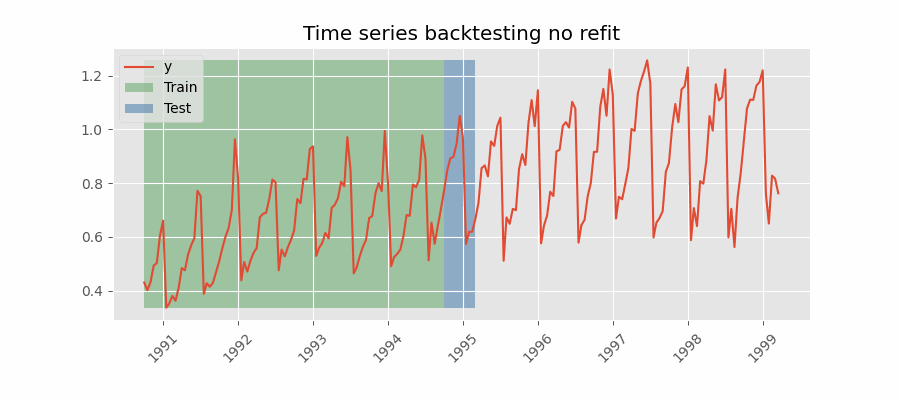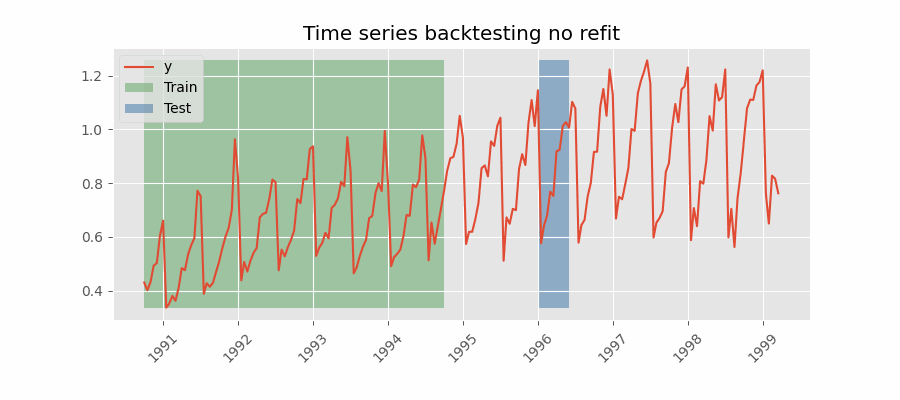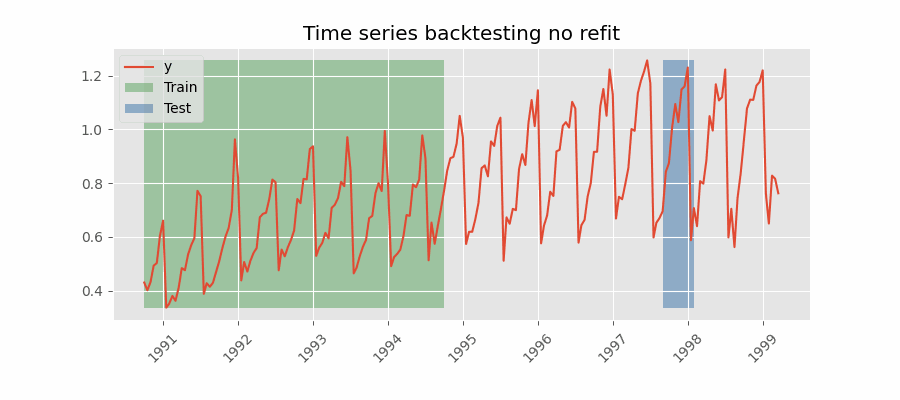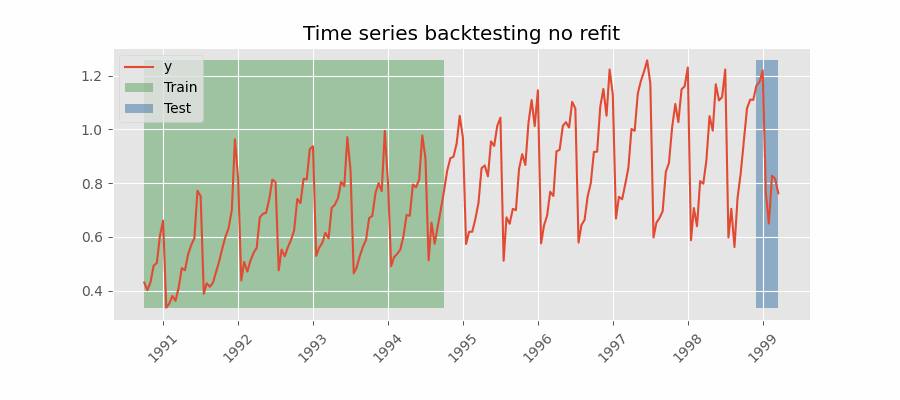
El método de validación más adecuada dependerá de cuál sea la estrategia seguida en la puesta en producción, en concreto, de si el modelo se va a reentrenar periódicamente o no antes de que se ejecute el proceso de predicción. Independientemente de la estrategia utilizada, es importante no incluir los datos de test en el proceso de búsqueda para no caer en problemas de overfitting.
Librerías¶
Las librerías utilizadas en este documento son:
# Tratamiento de datos
# ==============================================================================
import numpy as np
import pandas as pd
# Gráficos
# ==============================================================================
import matplotlib.pyplot as plt
import seaborn as sns
import hvplot.pandas
%matplotlib inline
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
plt.style.use('fivethirtyeight')
plt.rcParams['lines.linewidth'] = 1.5
plt.rcParams['font.size'] = 10
# Modelado y Forecasting
# ==============================================================================
from skforecast.ForecasterAutoreg import ForecasterAutoreg
from skforecast.model_selection import grid_search_forecaster
from skforecast.model_selection import backtesting_forecaster
from skforecast.ForecasterSarimax import ForecasterSarimax
from skforecast.model_selection_sarimax import backtesting_sarimax
from skforecast.model_selection_sarimax import grid_search_sarimax
from sklearn.linear_model import Ridge
from sklearn.preprocessing import StandardScaler
from pmdarima import ARIMA
# Configuración warnings
# ==============================================================================
import warnings
warnings.filterwarnings('ignore')
# Descarga de datos
# ==============================================================================
url = ('https://raw.githubusercontent.com/JoaquinAmatRodrigo/Estadistica-machine-learning-python/' +
'master/data/visitas_por_dia_web_cienciadedatos.csv')
datos = pd.read_csv(url, sep=',')
datos.info()
La columna date se ha almacenado como string. Para convertirla en formato fecha, se emplea la función pd.to_datetime(). Una vez en formato datetime, y para hacer uso de las funcionalidades de pandas, se establece como índice. Además, dado que los datos son de carácter diario, se indica la frecuencia ('1D').
# Conversión del formato fecha
# ==============================================================================
datos['date'] = pd.to_datetime(datos['date'], format='%d/%m/%y')
datos = datos.set_index('date')
datos = datos.asfreq('1D')
datos = datos.sort_index()
datos.head(3)
# Verificar que un índice temporal está completo
# ==============================================================================
(datos.index == pd.date_range(
start = datos.index.min(),
end = datos.index.max(),
freq = datos.index.freq)
).all()
print(f"Valores missing: {datos.isnull().any(axis=1).sum()}")
El set de datos empieza el 2020-07-01 y termina el 2021-08-22. Se dividen los datos en 3 conjuntos, uno de entrenamiento, uno de validación y otro de test.
# Separación datos train-test
# ==============================================================================
fin_train = '2021-03-30 23:59:00'
fin_validacion = '2021-06-30 23:59:00'
datos_train = datos.loc[: fin_train, :]
datos_val = datos.loc[fin_train:fin_validacion, :]
datos_test = datos.loc[fin_validacion:, :]
print(f"Fechas train : {datos_train.index.min()} --- {datos_train.index.max()} (n={len(datos_train)})")
print(f"Fechas validación : {datos_val.index.min()} --- {datos_val.index.max()} (n={len(datos_val)})")
print(f"Fechas test : {datos_test.index.min()} --- {datos_test.index.max()} (n={len(datos_test)})")
Exploración gráfica¶
Cuando se quiere generar un modelo de forecasting, es importante representar los valores de la serie temporal. Esto permite identificar patrones tales como tendencias y estacionalidad.
Serie temporal completa
# Gráfico serie temporal
# ==============================================================================
# fig, ax = plt.subplots(figsize=(12, 4))
# datos_train.users.plot(ax=ax, label='train', linewidth=1)
# datos_val.users.plot(ax=ax, label='val', linewidth=1)
# datos_test.users.plot(ax=ax, label='test', linewidth=1)
# ax.set_title('Visitas diarias a cienciadedatos.net')
# ax.legend();
plot_train = datos_train.users.hvplot.line(label='train')
plot_val = datos_val.users.hvplot.line(label='val')
plot_test = datos_test.users.hvplot.line(label='test')
layout = plot_train * plot_val * plot_test
layout = layout.opts(title='Visitas diarias a cienciadedatos.net', ylabel='users')
layout = layout.opts(height=300, width=550)
layout
Estacionalidad anual, mensual y semanal
# Gráfico boxplot para estacionalidad anual
# ==============================================================================
# fig, ax = plt.subplots(figsize=(7, 3.5))
# datos['mes'] = datos.index.month
# datos.boxplot(column='users', by='mes', ax=ax,)
# datos.groupby('mes')['users'].median().plot(style='o-', linewidth=0.8, ax=ax)
# ax.set_ylabel('users')
# ax.set_title('Distribución de visitas por mes')
# fig.suptitle('');
datos['mes'] = datos.index.month
boxplot = datos.sort_values('mes').hvplot.box(
y = 'users',
by = 'mes',
legend = False,
box_fill_color = None,
outlier_fill_color = None
)
lineplot = datos.groupby('mes')['users'].median().hvplot.line(legend=False)
scatterplot = datos.groupby('mes')['users'].median().hvplot.scatter(legend=False)
layout = boxplot * lineplot * scatterplot
layout = layout.opts(title='Distribución de visitas por mes', ylabel='users')
layout = layout.opts(height=300, width=500)
layout
# Gráfico boxplot para estacionalidad mensual
# ==============================================================================
# fig, ax = plt.subplots(figsize=(9, 3.5))
# datos['dia_mes'] = pd.Series(datos.index).dt.day.values
# datos.boxplot(column='users', by='dia_mes', ax=ax,)
# datos.groupby('dia_mes')['users'].median().plot(style='o-', linewidth=0.8, ax=ax)
# ax.set_ylabel('users')
# ax.set_title('Distribución de visitas por día del mes')
# fig.suptitle('');
datos['dia_mes'] = pd.Series(datos.index).dt.day.values
boxplot = datos.hvplot.box(
y = 'users',
by = 'dia_mes',
legend = False,
box_fill_color = None,
outlier_fill_color = None
)
lineplot = datos.groupby('dia_mes')['users'].median().hvplot.line(legend=False)
scatterplot = datos.groupby('dia_mes')['users'].median().hvplot.scatter(legend=False)
layout = boxplot * lineplot * scatterplot
layout = layout.opts(title='Distribución de visitas por día del mes', ylabel='users')
layout = layout.opts(height=300, width=500)
layout
# Gráfico boxplot para estacionalidad semanal
# ==============================================================================
# fig, ax = plt.subplots(figsize=(7, 3.5))
# datos['dia_semana'] = datos.index.day_of_week + 1
# datos.boxplot(column='users', by='dia_semana', ax=ax)
# datos.groupby('dia_semana')['users'].median().plot(style='o-', linewidth=0.8, ax=ax)
# ax.set_ylabel('users')
# ax.set_title('Distribución visitas por día de la semana')
# fig.suptitle('');
datos['dia_semana'] = datos.index.day_of_week + 1
boxplot = datos.sort_values('dia_semana').hvplot.box(
y = 'users',
by = 'dia_semana',
legend = False,
box_fill_color = None,
outlier_fill_color = None
)
lineplot = datos.groupby('dia_semana')['users'].median().hvplot.line(legend=False)
scatterplot = datos.groupby('dia_semana')['users'].median().hvplot.scatter(legend=False)
layout = boxplot * lineplot * scatterplot
layout = layout.opts(
title = 'Distribución de visitas por día de la semana',
ylabel = 'users'
)
layout = layout.opts(height=300, width=500)
layout
Al no disponer de dos años de histórico completos, no se puede determinar si existe una estacionalidad anual. Sí se aprecia una estacionalidad semanal, con una reducción del tráfico web los fines de semana.
Gráficos de autocorrelación
# Gráfico autocorrelación
# ==============================================================================
fig, ax = plt.subplots(figsize=(5, 2))
plot_acf(datos.users, ax=ax, lags=50)
plt.show()
# Gráfico autocorrelación parcial
# ==============================================================================
fig, ax = plt.subplots(figsize=(5, 2))
plot_pacf(datos.users, ax=ax, lags=50)
plt.show()
Los gráficos de autocorrelación y autocorrelación parcial muestran una clara asociación entre el número de usuarios un día y los días anteriores. Este tipo de correlación, es un indicativo de que los modelos autorregresivos pueden funcionar bien.
Modelo autoregresivo recursivo¶
Se crea y entrena un modelo autorregresivo recursivo (ForecasterAutoreg) a partir de un modelo de regresión lineal con penalización Ridge y una ventana temporal de 2 semanas (14 lags). Esto último significa que, para cada predicción, se utilizan como predictores el tráfico que tuvo la página los 14 días anteriores.
Los modelos Ridge requieren que los predictores se estandaricen. Con este fin, se utiliza el argumento transformer_y para incorporar un StandarScaler en el forecaster. Para conocer más sobre el uso dtransformers consultar Forecasting with scikit-learn and transformers pipelines.
Entrenamiento del Forecaster¶
# Crear y entrenar forecaster
# ==============================================================================
forecaster = ForecasterAutoreg(
regressor = Ridge(random_state=123),
lags = 14,
transformer_y = StandardScaler(),
forecaster_id = 'visitas_web'
)
forecaster.fit(y=datos_train.users)
forecaster
Predicción (backtest)¶
Se evalúa el comportamiento que habría tenido el modelo si se hubiese entrenado con los datos desde 2020-07-01 al 2021-06-30 y, después, se realizasen predicciones de 7 en 7 días sin reentrenar el modelo. A este tipo de evaluación se le conoce como backtesting, y puede aplicarse fácilmente con la función backtesting_forecaster(). Esta función devuelve, además de las predicciones, una métrica de error.
# Backtest
# ==============================================================================
metrica, predicciones = backtesting_forecaster(
forecaster = forecaster,
y = datos.users,
initial_train_size = len(datos.loc[:fin_validacion]),
steps = 7,
refit = False,
fixed_train_size = False,
metric = 'mean_absolute_error',
verbose = True,
show_progress = False
)
print(f'Error backtest: {metrica}')
predicciones.head(5)
# Gráfico
# ==============================================================================
# fig, ax = plt.subplots(figsize=(10, 3))
# datos_test.loc[predicciones.index, 'users'].plot(ax=ax, linewidth=2, label='test')
# predicciones.plot(linewidth=2, label='predicción', ax=ax)
# ax.set_title('Predicción (Autoreg-Ridge) vs vistas reales')
# ax.legend();
plot_test = datos_test.users.hvplot.line(label='test')
plot_predict = predicciones.hvplot.line(label='predicción')
layout = plot_test * plot_predict
layout = layout.opts(
title = 'Predicción (Autoreg-Ridge) vs vistas reales',
ylabel = 'users',
legend_position = 'bottom_left'
)
layout = layout.opts(height=300, width=550)
layout
Optimización de hiperparámetros (tuning)¶
En el apartado anterior, se han utilizado los primeros 14 lags como predictores y un modelo Ridge con los hiperparámetros por defecto. Sin embargo, no hay ninguna razón por la que estos valores sean los más adecuados.
Con el objetivo de identificar la mejor combinación de lags e hiperparámetros, se recurre a un Grid Search. Este proceso consiste en entrenar un modelo con cada combinación de hiperparámetros y lags, y evaluar su capacidad predictiva mediante backtesting.
En el proceso de búsqueda es importante evaluar los modelos utilizando únicamente los datos de validación y no incluir los de test, estos se utilizan solo en último lugar para evaluar al modelo final.
# Grid search de hiperparámetros
# ==============================================================================
forecaster = ForecasterAutoreg(
regressor = Ridge(random_state=123),
lags = 14,
transformer_y = StandardScaler(),
forecaster_id = 'visitas_web'
)
# Hiperparámetros del regresor
param_grid = {'alpha': np.logspace(-3, 3, 10)}
# Lags utilizados como predictores
lags_grid = [7, 14, 21, [7, 14, 21]]
resultados_grid = grid_search_forecaster(
forecaster = forecaster,
y = datos.loc[:fin_validacion, 'users'],
param_grid = param_grid,
lags_grid = lags_grid,
steps = 7,
metric = 'mean_absolute_error',
refit = False,
initial_train_size = len(datos_train),
fixed_train_size = False,
return_best = True,
show_progress = True,
verbose = False
)
# Resultados Grid Search
# ==============================================================================
resultados_grid.head(10)
Los mejores resultados se obtienen si se utilizan los lags [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14] y una configuración de Ridge {'alpha': 2.154}. Al indicar return_best = True en la función grid_search_forecaster(), al final del proceso, se reentrena automáticamente el objeto forecaster con la mejor configuración encontrada y el set de datos completo.
forecaster
Una vez identificado el mejor modelo, se entrena utilizando tanto el conjunto de entrenamiento como el de validación y se calcula su error con el conjunto de test.
# Backtest modelo final (conjunto de test)
# ==============================================================================
metrica, predicciones = backtesting_forecaster(
forecaster = forecaster,
y = datos.users,
initial_train_size = len(datos.loc[:fin_validacion, :]),
steps = 7,
refit = False,
fixed_train_size = False,
metric = 'mean_absolute_error',
verbose = False,
show_progress = True
)
print(f'Error backtest: {metrica}')
Tras la optimización de lags e hiperparámetros, se ha conseguido reducir el error de predicción.
Modelo ARIMA¶
Un modelo SARIMAX (Seasonal Autoregressive Integrated Moving-Average with Exogenous Regressors) es una generalización del modelo ARIMA que incorpora tanto la estacionalidad como variables exógenas. Los modelos SARIMAX figuran entre los modelos estadísticos de forecasting más utilizados y ofrecen excelentes resultados.
Skforecast utiliza la implementación del model ARIMA de pmdarima junto con el ForecasterSarimax. Y, con las funciones backtesting_sarimax() y grid_search_sarimax() del módulo model_selection_sarimax, se puede realizar su validación y optimización.
# ForecasterSarimax
# ==============================================================================
forecaster_sarimax = ForecasterSarimax(
regressor = ARIMA(order=(14, 0, 0), maxiter=250),
fit_kwargs = {'disp': 0},
forecaster_id = 'visitas_web_sarimax'
)
# Backtest ARIMA
# ==============================================================================
metrica, predicciones = backtesting_sarimax(
forecaster = forecaster_sarimax,
y = datos.users,
initial_train_size = len(datos.loc[:fin_validacion]),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
verbose = False,
show_progress = True
)
print(f'Error backtest: {metrica}')
predicciones.head(5)
# fig, ax = plt.subplots(figsize=(10, 3))
# datos_test.loc[predicciones.index, 'users'].plot(linewidth=2, label='test', ax=ax)
# predicciones.plot(linewidth=2, label='predicción', ax=ax)
# ax.set_title('Predicción (ARIMA) vs vistas reales')
# ax.legend();
plot_test = datos_test.users.hvplot.line(label='test')
plot_predict = predicciones['pred'].hvplot.line(label='predicción')
layout = plot_test * plot_predict
layout = layout.opts(
title = 'Predicción (ARIMA) vs vistas reales',
ylabel = 'users',
legend_position = 'bottom_left'
)
layout = layout.opts(height=300, width=550)
layout
Optimización de hiperparámetros (tuning)¶
Al igual que la mayoría de modelos, ARIMA tienen una serie de hiperparámetros que controlan su comportamiento:
p: número de lags incluidos como predictores en el modelo autoregresivo.
d: número de veces que se diferencian los datos, esto es el número de veces que a cada valor se le resta el valor anterior.
q: tamaño de ventana para la media móvil.
En la implementación de pmdarima, estos hiperparámetros se indican a través del argumento order. Dos buenas referencias para conocer más detalles de los modelos ARIMA son: https://openforecast.org/adam/ARIMA.html y https://otexts.com/fpp3/arima.html.
Con la función grid_search_sarimax se puede realizar una búsqueda de hiperparámetros comparando los modelos acorde a una métrica obtenida por validación cruzada o backtesting, o por las métricas aic y bic. Otras estrategias para la optimización de hiperparámetros.
# Grid search de hiperparámetros
# ==============================================================================
param_grid = {'order': [(14, 0, 0), (14, 2, 0), (14, 1, 0), (14, 1, 1), (14, 1, 4),
(21, 0, 0), (21, 0, 0), (21, 1, 0), (21, 1, 1), (21, 1, 4)]}
results = grid_search_sarimax(
forecaster = forecaster_sarimax,
y = datos.users,
param_grid = param_grid,
initial_train_size = len(datos.loc[:fin_validacion]),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
return_best = True,
verbose = False
)
results
# Backtest modelo final con datos de test
# ==============================================================================
metrica, predicciones = backtesting_sarimax(
forecaster = forecaster_sarimax,
y = datos.users,
initial_train_size = len(datos.loc[:fin_validacion]),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
verbose = False,
show_progress = True
)
print(f'Error backtest: {metrica}')
Forecasting con variables exógenas¶
En el ejemplo anterior, se han utilizado como predictores únicamente lags de la propia variable objetivo. En ciertos escenarios, es posible disponer de información sobre otras variables, cuyo valor a futuro se conoce, y que pueden servir como predictores adicionales en el modelo. Algunos ejemplos típicos son:
Festivos (local, nacional...)
Mes del año
Día de la semana
Hora del día
En este caso de uso, el análisis gráfico mostraba evidencias de que, los fines de semana, el número de visitas a la web se reduce. El día de la semana al que corresponde cada fecha puede saberse a futuro, por lo que se puede emplear como variable exógena. Véase cómo afecta a los modelos si se incluye como predictor está información.
# Creación de nuevas variables exógenas
# ==============================================================================
datos = datos.drop(columns=['mes', 'dia_mes'])
# One hot encoding del día de la semana y la hora del día
datos = pd.get_dummies(datos, columns=['dia_semana'], dtype='int64')
datos.head(3)
# Separación datos train-test
# ==============================================================================
datos_train = datos.loc[: fin_train, :]
datos_val = datos.loc[fin_train:fin_validacion, :]
datos_test = datos.loc[fin_validacion:, :]
ForecasterAutoreg¶
# Crear y entrenar forecaster
# ==============================================================================
forecaster = ForecasterAutoreg(
regressor = Ridge(alpha=2.15, random_state=123),
lags = 14,
transformer_y = StandardScaler(),
forecaster_id = 'visitas_web'
)
col_exog = [column for column in datos.columns if column.startswith(('dia'))]
forecaster.fit(y=datos_train.users, exog=datos_train[col_exog])
# Backtest modelo con variables exógenas
# ==============================================================================
metrica, predicciones = backtesting_forecaster(
forecaster = forecaster,
y = datos.users,
exog = datos[col_exog],
initial_train_size = len(datos.loc[:fin_validacion, :]),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
verbose = False,
show_progress = True
)
print(f'Error backtest: {metrica}')
predicciones.head(5)
ARIMA¶
# ForecasterSarimax
# ==============================================================================
forecaster_sarimax = ForecasterSarimax(
regressor = ARIMA(
order = (21, 1, 1),
seasonal_order = (0,0,0,0),
maxiter = 250
),
fit_kwargs = {'disp': 0},
forecaster_id = 'web_traffic_sarimax'
)
# Backtest modelo con variables exógenas
# ==============================================================================
metrica, predicciones = backtesting_sarimax(
forecaster = forecaster_sarimax,
y = datos.users,
exog = datos[col_exog],
initial_train_size = len(datos.loc[:fin_validacion]),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
verbose = True,
show_progress = False
)
print(f'Error backtest: {metrica}')
predicciones.head(5)
Intervalos de predicción¶
Tanto la función backtesting_forecaster como backtesting_sarimax permiten obtener, además de las predicciones, sus intervalos.
# Backtest modelo con variables exógenas
# ==============================================================================
metrica, predicciones = backtesting_sarimax(
forecaster = forecaster_sarimax,
y = datos.users,
exog = datos[col_exog],
initial_train_size = len(datos.loc[:fin_validacion]),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
alpha = 0.05,
verbose = False,
show_progress = True
)
print(f'Error backtest: {metrica}')
predicciones.head(5)
# fig, ax = plt.subplots(figsize=(10, 3))
# datos_test.loc[predicciones.index, 'users'].plot(linewidth=2, label='test', ax=ax)
# predicciones.iloc[:, 0].plot(linewidth=2, label='predicción', ax=ax)
# ax.set_title('Predicción (ARIMA) vs vistas reales')
# ax.fill_between(
# predicciones.index,
# predicciones.iloc[:, 1],
# predicciones.iloc[:, 2],
# alpha = 0.2,
# color = 'red',
# label = 'Intervalo predicción'
# )
# ax.legend();
plot_test = datos_test.users.hvplot.line(label='test')
plot_predict = predicciones['pred'].hvplot.line(label='predicción')
plot_intervalo = predicciones.hvplot.area(
y = 'lower_bound',
y2 = 'upper_bound',
color = 'red',
alpha = 0.2,
label = 'intervalo predicción'
)
layout = plot_intervalo * plot_test * plot_predict
layout = layout.opts(
title = 'Predicción (ARIMA) vs vistas reales',
ylabel = 'users',
legend_position = 'bottom_left'
)
layout = layout.opts(height=300, width=550)
layout
Conclusión¶
El modelo que consigue mejores resultados es el modelo ARIMA.
| Modelo | Variables exógenas | MAE backtest |
|---|---|---|
| ARIMA | True | 181.3 |
| ARIMA | False | 181.8 |
| Autoregressive-ridge | True | 195.9 |
| Autoregressive-ridge | False | 216.4 |
Posibles mejoras del modelo:
Incluir como predictor si el día es festivo nacional.
Utilizar un modelo autoregresivo con modelos no lineales, por ejemplo random forest o gradient boosting. Forecasting series temporales con gradient boosting: Skforecast, XGBoost, LightGBM y CatBoost.
Utilizar un modelo direct multi-step.
Información de sesión¶
import session_info
session_info.show(html=False)
¿Cómo citar este documento?
Predicción (forecasting) visitas página web con Python by Joaquín Amat Rodrigo and Javier Escobar Ortiz, available under a Attribution 4.0 International (CC BY 4.0) at https://www.cienciadedatos.net/py36-forecasting-visitas-web-machine-learning.html
¿Te ha gustado el artículo? Tu ayuda es importante
Mantener un sitio web tiene unos costes elevados, tu contribución me ayudará a seguir generando contenido divulgativo gratuito. ¡Muchísimas gracias! 😊
This work by Joaquín Amat Rodrigo and Javier Escobar Ortiz is licensed under a Creative Commons Attribution 4.0 International License.