更多关于预测的信息请访问 cienciadedatos.net
- 使用 Python 的 ARIMA 和 SARIMAX 模型
- 使用机器学习进行时间序列预测
- 使用梯度提升方法进行时间序列预测:XGBoost、LightGBM 和 CatBoost
- 使用 XGBoost 进行时间序列预测
- 全局预测模型:多序列预测
- 全局预测模型:单序列与多序列建模的对比分析
- 概率性预测
- 深度学习预测
- 机器学习预测能源需求
- 机器学习预测网站流量
- 间歇性需求预测
- 基于树模型建模时间序列趋势
- 使用 Python 预测比特币价格
- 集成学习提升预测效果
- 可解释性预测模型
- 减轻新冠疫情对预测模型的影响
- 缺失值时间序列预测

引言¶
能源需求预测在电力生产、分配和利用的资源管理与规划中起着至关重要的作用。预测能源需求是一项复杂的任务,受天气模式、经济状况和社会行为等多种因素影响。本文将探讨如何利用机器学习方法构建预测模型,以预测能源需求。
时间序列与预测
时间序列是指按时间顺序排列的数据序列,时间间隔可以相等也可以不等。预测过程包括预测时间序列的未来值,可以仅基于其过去行为进行建模(自回归),也可以结合其他外部变量。
在处理时间序列时,通常不仅仅需要预测下一个时刻($t_{+1}$),更常见的目标是预测未来一段区间(($t_{+1}$), ..., ($t_{+n}$))或更远的未来时刻($t_{+n}$)。为实现这类预测,可以采用多种策略,skforecast 针对单变量时间序列预测实现了以下方法:
- 递归多步预测:由于预测 $t_{n}$ 需要 $t_{n-1}$ 的值,而 $t_{n-1}$ 是未知的,因此采用递归过程,每次新预测都基于上一次的结果。这一过程称为递归预测或递归多步预测,可通过
ForecasterRecursive类轻松实现。

- 直接多步预测:该方法为预测区间内的每一步分别训练一个模型。例如,要预测时间序列的未来5个值,就需要训练5个不同的模型,每个模型对应一个预测步长,因此各步预测结果相互独立。整个过程可通过
ForecasterDirect类自动完成。
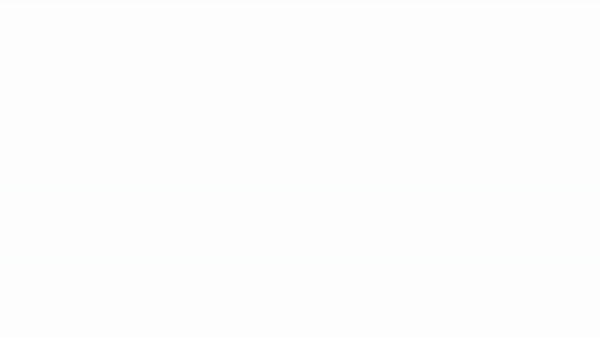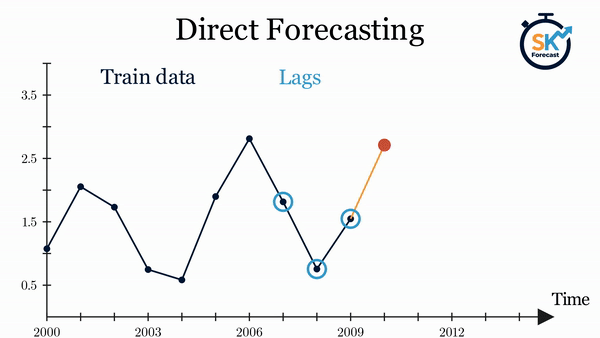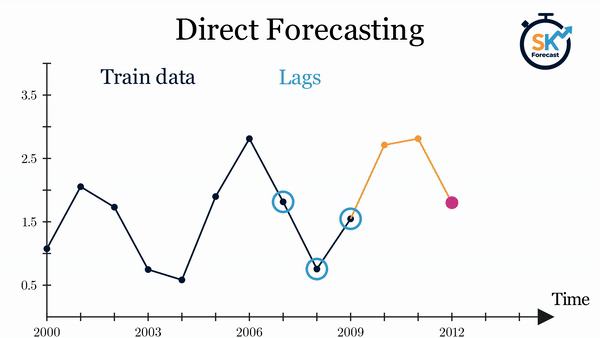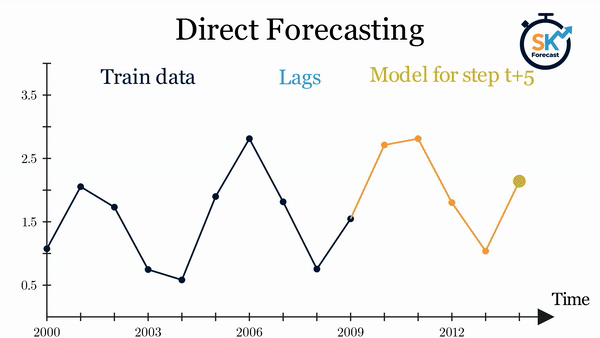
- 多输出预测:某些机器学习模型(如长短期记忆网络 LSTM)可以一次性同时预测多个序列值(one-shot)。该策略在
ForecasterRnn类中实现。
✏️ 注意
以下是使用梯度提升方法进行时间序列预测的两个优秀案例:
库¶
本文使用的库如下:
# 数据处理
# ==============================================================================
import numpy as np
import pandas as pd
from astral.sun import sun
from astral import LocationInfo
from skforecast.datasets import fetch_dataset
from feature_engine.datetime import DatetimeFeatures
from feature_engine.creation import CyclicalFeatures
from feature_engine.timeseries.forecasting import WindowFeatures
# 绘图
# ==============================================================================
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from skforecast.plot import plot_residuals
import plotly.graph_objects as go
import plotly.io as pio
import plotly.offline as poff
pio.templates.default = "seaborn"
poff.init_notebook_mode(connected=True)
plt.style.use('seaborn-v0_8-darkgrid')
plt.rcParams.update({'font.size': 8})
# 建模与预测
# ==============================================================================
import skforecast
import lightgbm
import sklearn
from lightgbm import LGBMRegressor
from sklearn.preprocessing import PolynomialFeatures
from sklearn.feature_selection import RFECV
from skforecast.recursive import ForecasterEquivalentDate, ForecasterRecursive
from skforecast.direct import ForecasterDirect
from skforecast.model_selection import TimeSeriesFold, bayesian_search_forecaster, backtesting_forecaster
from skforecast.feature_selection import select_features
from skforecast.preprocessing import RollingFeatures
from skforecast.plot import calculate_lag_autocorrelation, plot_residuals
from skforecast.metrics import calculate_coverage
import shap
# 警告配置
# ==============================================================================
import warnings
warnings.filterwarnings('once')
color = '\033[1m\033[38;5;208m'
print(f"{color}Version skforecast: {skforecast.__version__}")
print(f"{color}Version scikit-learn: {sklearn.__version__}")
print(f"{color}Version lightgbm: {lightgbm.__version__}")
print(f"{color}Version pandas: {pd.__version__}")
print(f"{color}Version numpy: {np.__version__}")
Version skforecast: 0.19.0 Version scikit-learn: 1.7.2 Version lightgbm: 4.6.0 Version pandas: 2.3.3 Version numpy: 2.3.4
数据¶
本例使用的数据为澳大利亚维多利亚州 2011-12-31 至 2014-12-31 的电力需求(MW)时间序列。数据来源于 R tsibbledata 包。数据集包含 5 列和 52,608 条完整记录。各列信息如下:
- Time:记录的日期和时间。
- Date:记录的日期。
- Demand:电力需求(MW)。
- Temperature:维多利亚州首府墨尔本的温度。
- Holiday:是否为公共假日。
# 数据下载
# ==============================================================================
data = fetch_dataset(name='vic_electricity', raw=True)
data.info()
╭──────────────────────────── vic_electricity ─────────────────────────────╮ │ Description: │ │ Half-hourly electricity demand for Victoria, Australia │ │ │ │ Source: │ │ O'Hara-Wild M, Hyndman R, Wang E, Godahewa R (2022).tsibbledata: Diverse │ │ Datasets for 'tsibble'. https://tsibbledata.tidyverts.org/, │ │ https://github.com/tidyverts/tsibbledata/. │ │ https://tsibbledata.tidyverts.org/reference/vic_elec.html │ │ │ │ URL: │ │ https://raw.githubusercontent.com/skforecast/skforecast- │ │ datasets/main/data/vic_electricity.csv │ │ │ │ Shape: 52608 rows x 5 columns │ ╰──────────────────────────────────────────────────────────────────────────╯
<class 'pandas.core.frame.DataFrame'> RangeIndex: 52608 entries, 0 to 52607 Data columns (total 5 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 Time 52608 non-null object 1 Demand 52608 non-null float64 2 Temperature 52608 non-null float64 3 Date 52608 non-null object 4 Holiday 52608 non-null bool dtypes: bool(1), float64(2), object(2) memory usage: 1.7+ MB
Time 列以 string 格式存储。可使用 pd.to_datetime() 函数将其转换为 datetime 类型。转换后,为了方便使用 pandas 的功能,将其设置为索引。由于数据每 30 分钟记录一次,因此还需指定频率 '30min'。
# 数据预处理
# ==============================================================================
data = data.copy()
data['Time'] = pd.to_datetime(data['Time'], format='%Y-%m-%dT%H:%M:%SZ')
data = data.set_index('Time')
data = data.asfreq('30min')
data = data.sort_index()
data.head(2)
| Demand | Temperature | Date | Holiday | |
|---|---|---|---|---|
| Time | ||||
| 2011-12-31 13:00:00 | 4382.825174 | 21.40 | 2012-01-01 | True |
| 2011-12-31 13:30:00 | 4263.365526 | 21.05 | 2012-01-01 | True |
在处理时间序列时,首先要检查序列是否完整,即是否存在缺失值。
# 验证时间索引是否完整
# ==============================================================================
start_date = data.index.min()
end_date = data.index.max()
complete_date_range = pd.date_range(start=start_date, end=end_date, freq=data.index.freq)
is_index_complete = (data.index == complete_date_range).all()
print(f"Index complete: {is_index_complete}")
print(f"Number of rows with missing values: {data.isnull().any(axis=1).mean()}")
Index complete: True Number of rows with missing values: 0.0
# 填补时间索引中的缺口
# ==============================================================================
# data.asfreq(freq='30min', fill_value=np.nan)
虽然数据的时间间隔为 30 分钟,但本例的目标是建立能够预测每小时电力需求的模型,因此需要对数据进行聚合。此类转换可通过 Pandas 的 DatetimeIndex 索引和 resample() 方法轻松实现。
正确使用 closed='left' 和 label='right' 参数非常重要,以避免在训练中引入未来信息(信息泄露))。假设可用的时间点为 10:10、10:30、10:45、11:00、11:12 和 11:30。要获得每小时的平均值,分配给 11:00 的值应仅使用 10:10、10:30 和 10:45 的数据计算;分配给 12:00 的值应仅使用 11:00、11:12 和 11:30 的数据计算。

11:00 的平均值不包含 11:00 的点值,因为实际上该时刻的值并不可用。
# 以 1 小时为间隔进行聚合
# ==============================================================================
# 删除 Date 列,避免聚合时报错。
data = data.drop(columns="Date")
data = (
data
.resample(rule="h", closed="left", label="right")
.agg({
"Demand": "mean",
"Temperature": "mean",
"Holiday": "mean",
})
)
data
| Demand | Temperature | Holiday | |
|---|---|---|---|
| Time | |||
| 2011-12-31 14:00:00 | 4323.095350 | 21.225 | 1.0 |
| 2011-12-31 15:00:00 | 3963.264688 | 20.625 | 1.0 |
| 2011-12-31 16:00:00 | 3950.913495 | 20.325 | 1.0 |
| 2011-12-31 17:00:00 | 3627.860675 | 19.850 | 1.0 |
| 2011-12-31 18:00:00 | 3396.251676 | 19.025 | 1.0 |
| ... | ... | ... | ... |
| 2014-12-31 09:00:00 | 4069.625550 | 21.600 | 0.0 |
| 2014-12-31 10:00:00 | 3909.230704 | 20.300 | 0.0 |
| 2014-12-31 11:00:00 | 3900.600901 | 19.650 | 0.0 |
| 2014-12-31 12:00:00 | 3758.236494 | 18.100 | 0.0 |
| 2014-12-31 13:00:00 | 3785.650720 | 17.200 | 0.0 |
26304 rows × 3 columns
数据集起始于 2011-12-31 14:00:00,结束于 2014-12-31 13:00:00。为保证数据完整,前 10 条和最后 13 条记录被舍弃,使其起始于 2012-01-01 00:00:00,结束于 2014-12-30 23:00:00。此外,为了优化模型超参数并评估其预测能力,数据被划分为训练集、验证集和测试集三部分。
# 划分数据为 train-val-test
# ==============================================================================
data = data.loc['2012-01-01 00:00:00':'2014-12-30 23:00:00', :].copy()
end_train = '2013-12-31 23:59:00'
end_validation = '2014-11-30 23:59:00'
data_train = data.loc[: end_train, :].copy()
data_val = data.loc[end_train:end_validation, :].copy()
data_test = data.loc[end_validation:, :].copy()
print(f"Train dates : {data_train.index.min()} --- {data_train.index.max()} (n={len(data_train)})")
print(f"Validation dates : {data_val.index.min()} --- {data_val.index.max()} (n={len(data_val)})")
print(f"Test dates : {data_test.index.min()} --- {data_test.index.max()} (n={len(data_test)})")
Train dates : 2012-01-01 00:00:00 --- 2013-12-31 23:00:00 (n=17544) Validation dates : 2014-01-01 00:00:00 --- 2014-11-30 23:00:00 (n=8016) Test dates : 2014-12-01 00:00:00 --- 2014-12-30 23:00:00 (n=720)
图形探索¶
通过对时间序列进行图形化探索,可以有效识别趋势、模式和季节性变化,从而为选择最合适的预测模型提供指导。
时间序列绘图¶
完整时间序列
# 时间序列交互式绘图
# ==============================================================================
fig = go.Figure()
fig.add_trace(go.Scatter(x=data_train.index, y=data_train['Demand'], mode='lines', name='Train'))
fig.add_trace(go.Scatter(x=data_val.index, y=data_val['Demand'], mode='lines', name='Validation'))
fig.add_trace(go.Scatter(x=data_test.index, y=data_test['Demand'], mode='lines', name='Test'))
fig.update_layout(
title='Hourly energy demand',
xaxis_title="Time",
yaxis_title="Demand",
legend_title="Partition:",
width=800,
height=400,
margin=dict(l=20, r=20, t=35, b=20),
legend=dict(orientation="h", yanchor="top", y=1, xanchor="left", x=0.001)
)
#fig.update_xaxes(rangeslider_visible=True)
fig.show()
上图显示,电力需求具有年度季节性。7 月份有一个高峰,1 月至 3 月期间需求也有明显的高峰。
时间序列片段
由于时间序列的方差较大,单一图表难以观察到可能存在的日内模式。
# 时间序列局部放大图
# ==============================================================================
zoom = ('2013-05-01 14:00:00','2013-06-01 14:00:00')
fig, axs = plt.subplots(2, 1, figsize=(8, 4), gridspec_kw={"height_ratios": [1, 2]})
data["Demand"].plot(ax=axs[0], color="black", alpha=0.5)
axs[0].axvspan(zoom[0], zoom[1], color="blue", alpha=0.7)
axs[0].set_title("Electricity demand")
axs[0].set_xlabel("")
data.loc[zoom[0] : zoom[1], "Demand"].plot(ax=axs[1], color="blue")
axs[1].set_title(f"Zoom: {zoom[0]} to {zoom[1]}", fontsize=10)
plt.tight_layout()
plt.show()
当对时间序列进行放大观察时,可以明显看到每周的季节性特征:工作日(周一至周五)用电量较高,周末用电量较低。同时,每天的用电量与前一天存在明显相关性。
季节性图¶
季节性图是识别时间序列中季节性模式和趋势的有力工具。其方法是对每个季节的数值进行平均,然后将其随时间绘制出来。
# 年度、每周和每日季节性
# ==============================================================================
fig, axs = plt.subplots(2, 2, figsize=(8, 5), sharex=False, sharey=True)
axs = axs.ravel()
# 按月份统计需求分布
data['month'] = data.index.month
data.boxplot(column='Demand', by='month', ax=axs[0], flierprops={'markersize': 3, 'alpha': 0.3})
data.groupby('month')['Demand'].median().plot(style='o-', linewidth=0.8, ax=axs[0])
axs[0].set_ylabel('Demand')
axs[0].set_title('Demand distribution by month', fontsize=9)
# 按星期几统计需求分布
data['week_day'] = data.index.day_of_week + 1
data.boxplot(column='Demand', by='week_day', ax=axs[1], flierprops={'markersize': 3, 'alpha': 0.3})
data.groupby('week_day')['Demand'].median().plot(style='o-', linewidth=0.8, ax=axs[1])
axs[1].set_ylabel('Demand')
axs[1].set_title('Demand distribution by week day', fontsize=9)
# 按一天中的小时统计需求分布
data['hour_day'] = data.index.hour + 1
data.boxplot(column='Demand', by='hour_day', ax=axs[2], flierprops={'markersize': 3, 'alpha': 0.3})
data.groupby('hour_day')['Demand'].median().plot(style='o-', linewidth=0.8, ax=axs[2])
axs[2].set_ylabel('Demand')
axs[2].set_title('Demand distribution by the hour of the day', fontsize=9)
# 按星期几和小时统计需求分布
mean_day_hour = data.groupby(["week_day", "hour_day"])["Demand"].mean()
mean_day_hour.plot(ax=axs[3])
axs[3].set(
title = "Mean Demand during week",
xticks = [i * 24 for i in range(7)],
xticklabels = ["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"],
xlabel = "Day and hour",
ylabel = "Number of Demand"
)
axs[3].title.set_size(10)
fig.suptitle("Seasonality plots", fontsize=12)
fig.tight_layout()
存在年度季节性,6、7、8 月份的需求(中位数)较高,11、12、1、2、3 月份的需求峰值较高。存在每周季节性,周末需求较低。也存在日内季节性,16:00 至 21:00 期间需求下降。
自相关图¶
自相关图是确定自回归模型阶数的有力工具。自相关函数(ACF)衡量时间序列与其自身滞后版本之间的相关性。偏自相关函数(PACF)衡量时间序列与其自身滞后版本之间的相关性,同时控制所有更短滞后的影响。这些图有助于确定自回归模型中应包含的滞后数。
# 自相关图
# ==============================================================================
fig, ax = plt.subplots(figsize=(5, 2))
plot_acf(data['Demand'], ax=ax, lags=60)
plt.show()
# 偏自相关图
# ==============================================================================
fig, ax = plt.subplots(figsize=(5, 2))
plot_pacf(data['Demand'], ax=ax, lags=60)
plt.show()
# 偏自相关绝对值最大的前 10 个滞后
# ==============================================================================
calculate_lag_autocorrelation(
data = data['Demand'],
n_lags = 60,
sort_by = "partial_autocorrelation_abs"
).head(10)
| lag | partial_autocorrelation_abs | partial_autocorrelation | autocorrelation_abs | autocorrelation | |
|---|---|---|---|---|---|
| 0 | 1 | 0.949526 | 0.949526 | 0.949490 | 0.949490 |
| 1 | 25 | 0.761400 | -0.761400 | 0.731620 | 0.731620 |
| 2 | 2 | 0.657961 | -0.657961 | 0.836792 | 0.836792 |
| 3 | 26 | 0.634868 | 0.634868 | 0.622458 | 0.622458 |
| 4 | 24 | 0.308085 | -0.308085 | 0.785622 | 0.785622 |
| 5 | 19 | 0.291113 | 0.291113 | 0.302308 | 0.302308 |
| 6 | 27 | 0.281261 | -0.281261 | 0.488351 | 0.488351 |
| 7 | 21 | 0.269274 | 0.269274 | 0.537173 | 0.537173 |
| 8 | 20 | 0.201192 | 0.201192 | 0.414709 | 0.414709 |
| 9 | 9 | 0.184975 | 0.184975 | 0.037677 | 0.037677 |
自相关图显示,某一小时的需求与前几小时以及前几天同一小时的需求有很强的相关性。这种相关性表明自回归模型在本场景下可能非常有效。
基线¶
在面对预测问题时,建立基线模型非常重要。基线模型通常是非常简单的模型,用于评估更复杂模型是否值得实现。
Skforecast 可以通过 ForecasterEquivalentDate 类轻松创建基线模型。该模型也称为季节性朴素预测(Seasonal Naive Forecasting),其原理是直接返回前一季节同一时段的观测值(如前一周同一工作日、前一天同一小时等)。
根据前面的探索性分析,基线模型将采用前一天同一小时的值作为每小时的预测。
✏️ 注意
在接下来的代码单元中,将训练基线预测器并通过回测过程评估其预测能力。如果你对回测(backtesting)不熟悉,不必担心,本文后续会详细解释。现在只需知道,回测过程是用部分数据训练模型,再用未见过的数据评估其预测能力。该误差指标将作为后续更复杂模型预测能力的参考。
# 创建基线模型:前一天同一小时的值
# ==============================================================================
forecaster = ForecasterEquivalentDate(
offset = pd.DateOffset(days=1),
n_offsets = 1
)
# 训练预测器
# ==============================================================================
forecaster.fit(y=data.loc[:end_validation, 'Demand'])
forecaster
ForecasterEquivalentDate
General Information
- Estimator: NoneType
- Offset:
- Number of offsets: 1
- Aggregation function: mean
- Window size: 24
- Creation date: 2025-11-28 20:50:28
- Last fit date: 2025-11-28 20:50:28
- Skforecast version: 0.19.0
- Python version: 3.13.9
- Forecaster id: None
Training Information
- Training range: [Timestamp('2012-01-01 00:00:00'), Timestamp('2014-11-30 23:00:00')]
- Training index type: DatetimeIndex
- Training index frequency:
# 回测
# ==============================================================================
cv = TimeSeriesFold(
steps = 24,
initial_train_size = len(data.loc[:end_validation]),
refit = False
)
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
cv = cv,
metric = 'mean_absolute_error'
)
metric
| mean_absolute_error | |
|---|---|
| 0 | 308.375272 |
基线模型的误差可作为评估更复杂模型是否值得实现的参考。
递归多步预测¶
训练递归自回归模型 ForecasterRecursive,使用梯度提升回归器 LGBMRegressor 预测未来 24 小时的能源需求。
所用特征包括过去 24 小时的需求值(24 个滞后)以及过去 3 天的移动平均值。回归器的超参数均为默认值。
# 创建预测器
# ==============================================================================
window_features = RollingFeatures(stats=["mean"], window_sizes=24 * 3)
forecaster = ForecasterRecursive(
estimator = LGBMRegressor(random_state=15926, verbose=-1),
lags = 24,
window_features = window_features
)
# 训练预测器
# ==============================================================================
forecaster.fit(y=data.loc[:end_validation, 'Demand'])
forecaster
ForecasterRecursive
General Information
- Estimator: LGBMRegressor
- Lags: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]
- Window features: ['roll_mean_72']
- Window size: 72
- Series name: Demand
- Exogenous included: False
- Weight function included: False
- Differentiation order: None
- Creation date: 2025-11-28 20:50:28
- Last fit date: 2025-11-28 20:50:32
- Skforecast version: 0.19.0
- Python version: 3.13.9
- Forecaster id: None
Exogenous Variables
-
None
Data Transformations
- Transformer for y: None
- Transformer for exog: None
Training Information
- Training range: [Timestamp('2012-01-01 00:00:00'), Timestamp('2014-11-30 23:00:00')]
- Training index type: DatetimeIndex
- Training index frequency:
Estimator Parameters
-
{'boosting_type': 'gbdt', 'class_weight': None, 'colsample_bytree': 1.0, 'importance_type': 'split', 'learning_rate': 0.1, 'max_depth': -1, 'min_child_samples': 20, 'min_child_weight': 0.001, 'min_split_gain': 0.0, 'n_estimators': 100, 'n_jobs': None, 'num_leaves': 31, 'objective': None, 'random_state': 15926, 'reg_alpha': 0.0, 'reg_lambda': 0.0, 'subsample': 1.0, 'subsample_for_bin': 200000, 'subsample_freq': 0, 'verbose': -1}
Fit Kwargs
-
{}
回测¶
为获得模型预测能力的稳健估计,需进行回测。回测过程是针对测试集的每个观测点生成预测,模拟实际生产环境下的预测流程,并将预测值与真实值进行比较。
回测通过 backtesting_forecaster() 函数实现。本例中,模型用 2012-01-01 00:00 至 2014-11-30 23:00 的数据训练,每天 23:59 预测未来 24 小时。误差指标为平均绝对误差(MAE)。
强烈建议查阅 backtesting_forecaster() 函数文档,深入了解其功能,以便充分利用其分析模型预测能力的潜力。
# 回测
# ==============================================================================
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
cv = cv,
metric = 'mean_absolute_error',
verbose = True, # 设为 False 可避免打印
)
Information of folds
--------------------
Number of observations used for initial training: 25560
Number of observations used for backtesting: 720
Number of folds: 30
Number skipped folds: 0
Number of steps per fold: 24
Number of steps to exclude between last observed data (last window) and predictions (gap): 0
Fold: 0
Training: 2012-01-01 00:00:00 -- 2014-11-30 23:00:00 (n=25560)
Validation: 2014-12-01 00:00:00 -- 2014-12-01 23:00:00 (n=24)
Fold: 1
Training: No training in this fold
Validation: 2014-12-02 00:00:00 -- 2014-12-02 23:00:00 (n=24)
Fold: 2
Training: No training in this fold
Validation: 2014-12-03 00:00:00 -- 2014-12-03 23:00:00 (n=24)
Fold: 3
Training: No training in this fold
Validation: 2014-12-04 00:00:00 -- 2014-12-04 23:00:00 (n=24)
Fold: 4
Training: No training in this fold
Validation: 2014-12-05 00:00:00 -- 2014-12-05 23:00:00 (n=24)
Fold: 5
Training: No training in this fold
Validation: 2014-12-06 00:00:00 -- 2014-12-06 23:00:00 (n=24)
Fold: 6
Training: No training in this fold
Validation: 2014-12-07 00:00:00 -- 2014-12-07 23:00:00 (n=24)
Fold: 7
Training: No training in this fold
Validation: 2014-12-08 00:00:00 -- 2014-12-08 23:00:00 (n=24)
Fold: 8
Training: No training in this fold
Validation: 2014-12-09 00:00:00 -- 2014-12-09 23:00:00 (n=24)
Fold: 9
Training: No training in this fold
Validation: 2014-12-10 00:00:00 -- 2014-12-10 23:00:00 (n=24)
Fold: 10
Training: No training in this fold
Validation: 2014-12-11 00:00:00 -- 2014-12-11 23:00:00 (n=24)
Fold: 11
Training: No training in this fold
Validation: 2014-12-12 00:00:00 -- 2014-12-12 23:00:00 (n=24)
Fold: 12
Training: No training in this fold
Validation: 2014-12-13 00:00:00 -- 2014-12-13 23:00:00 (n=24)
Fold: 13
Training: No training in this fold
Validation: 2014-12-14 00:00:00 -- 2014-12-14 23:00:00 (n=24)
Fold: 14
Training: No training in this fold
Validation: 2014-12-15 00:00:00 -- 2014-12-15 23:00:00 (n=24)
Fold: 15
Training: No training in this fold
Validation: 2014-12-16 00:00:00 -- 2014-12-16 23:00:00 (n=24)
Fold: 16
Training: No training in this fold
Validation: 2014-12-17 00:00:00 -- 2014-12-17 23:00:00 (n=24)
Fold: 17
Training: No training in this fold
Validation: 2014-12-18 00:00:00 -- 2014-12-18 23:00:00 (n=24)
Fold: 18
Training: No training in this fold
Validation: 2014-12-19 00:00:00 -- 2014-12-19 23:00:00 (n=24)
Fold: 19
Training: No training in this fold
Validation: 2014-12-20 00:00:00 -- 2014-12-20 23:00:00 (n=24)
Fold: 20
Training: No training in this fold
Validation: 2014-12-21 00:00:00 -- 2014-12-21 23:00:00 (n=24)
Fold: 21
Training: No training in this fold
Validation: 2014-12-22 00:00:00 -- 2014-12-22 23:00:00 (n=24)
Fold: 22
Training: No training in this fold
Validation: 2014-12-23 00:00:00 -- 2014-12-23 23:00:00 (n=24)
Fold: 23
Training: No training in this fold
Validation: 2014-12-24 00:00:00 -- 2014-12-24 23:00:00 (n=24)
Fold: 24
Training: No training in this fold
Validation: 2014-12-25 00:00:00 -- 2014-12-25 23:00:00 (n=24)
Fold: 25
Training: No training in this fold
Validation: 2014-12-26 00:00:00 -- 2014-12-26 23:00:00 (n=24)
Fold: 26
Training: No training in this fold
Validation: 2014-12-27 00:00:00 -- 2014-12-27 23:00:00 (n=24)
Fold: 27
Training: No training in this fold
Validation: 2014-12-28 00:00:00 -- 2014-12-28 23:00:00 (n=24)
Fold: 28
Training: No training in this fold
Validation: 2014-12-29 00:00:00 -- 2014-12-29 23:00:00 (n=24)
Fold: 29
Training: No training in this fold
Validation: 2014-12-30 00:00:00 -- 2014-12-30 23:00:00 (n=24)
# 绘制预测值与真实值对比图
# ======================================================================================
fig = go.Figure()
trace1 = go.Scatter(x=data_test.index, y=data_test['Demand'], name="test", mode="lines")
trace2 = go.Scatter(x=predictions.index, y=predictions['pred'], name="prediction", mode="lines")
fig.add_trace(trace1)
fig.add_trace(trace2)
fig.update_layout(
title="Real value vs predicted in test data",
xaxis_title="Date time",
yaxis_title="Demand",
width=800,
height=400,
margin=dict(l=20, r=20, t=35, b=20),
legend=dict(orientation="h", yanchor="top", y=1.01, xanchor="left", x=0)
)
fig.show()
# 回测误差
# ==============================================================================
metric
| mean_absolute_error | |
|---|---|
| 0 | 225.521306 |
自回归模型的 MAE 低于基线模型。这说明自回归模型对次日电力需求的预测更为准确。
外生变量¶
目前为止,仅使用了时间序列的滞后值作为特征。实际上,还可以引入其他变量作为特征,这些变量称为外生变量(特征),其使用有助于提升模型的预测能力。需要特别注意的是,预测时必须已知外生变量的值。
常见的外生变量包括日历信息(如星期几、月份、年份或节假日)、气象变量(如温度、湿度、风速)以及经济变量(如通胀、利率)等。
⚠️ 警告
外生变量必须在预测时已知。例如,若将温度作为外生变量,则预测时必须已知下一小时的温度值。若温度未知,则无法进行预测。
气象变量应谨慎使用。实际部署时,未来气象条件并非已知,而是由气象服务预测。这些预测本身存在误差,会传递到预测模型中,导致模型预测能力下降。为预估模型实际表现,建议在训练时使用当时可获得的气象预测数据,而非真实观测值。
接下来,将基于日历信息、日出日落时间、温度和节假日等创建外生变量。这些新变量将被添加到训练集、验证集和测试集中,并作为特征用于自回归模型。
# 日历特征
# ==============================================================================
features_to_extract = [
'month',
'week',
'day_of_week',
'hour'
]
calendar_transformer = DatetimeFeatures(
variables = 'index',
features_to_extract = features_to_extract,
drop_original = True,
)
calendar_features = calendar_transformer.fit_transform(data)[features_to_extract]
# 日照特征
# ==============================================================================
location = LocationInfo(
latitude = -37.8,
longitude = 144.95,
timezone = 'Australia/Melbourne'
)
sunrise_hour = [
sun(location.observer, date=date, tzinfo=location.timezone)['sunrise']
for date in data.index
]
sunset_hour = [
sun(location.observer, date=date, tzinfo=location.timezone)['sunset']
for date in data.index
]
sunrise_hour = pd.Series(sunrise_hour, index=data.index).dt.round("h").dt.hour
sunset_hour = pd.Series(sunset_hour, index=data.index).dt.round("h").dt.hour
sun_light_features = pd.DataFrame({
'sunrise_hour': sunrise_hour,
'sunset_hour': sunset_hour
})
sun_light_features['daylight_hours'] = (
sun_light_features['sunset_hour'] - sun_light_features['sunrise_hour']
)
sun_light_features["is_daylight"] = np.where(
(data.index.hour >= sun_light_features["sunrise_hour"])
& (data.index.hour < sun_light_features["sunset_hour"]),
1,
0,
)
# 节假日特征
# ==============================================================================
holiday_features = data[['Holiday']].astype(int)
holiday_features['holiday_previous_day'] = holiday_features['Holiday'].shift(24)
holiday_features['holiday_next_day'] = holiday_features['Holiday'].shift(-24)
# 温度的滑动窗口
# ==============================================================================
wf_transformer = WindowFeatures(
variables = ["Temperature"],
window = ["1D", "7D"],
functions = ["mean", "max", "min"],
freq = "h",
)
temp_features = wf_transformer.fit_transform(data[['Temperature']])
# 合并所有外生变量
# ==============================================================================
assert all(calendar_features.index == sun_light_features.index)
assert all(calendar_features.index == temp_features.index)
assert all(calendar_features.index == holiday_features.index)
exogenous_features = pd.concat([
calendar_features,
sun_light_features,
temp_features,
holiday_features
], axis=1)
# 由于滑动平均的创建,序列开头会有缺失值;holiday_next_day 导致结尾也有缺失值。
exogenous_features = exogenous_features.iloc[7 * 24:, :]
exogenous_features = exogenous_features.iloc[:-24, :]
exogenous_features.head(3)
| month | week | day_of_week | hour | sunrise_hour | sunset_hour | daylight_hours | is_daylight | Temperature | Temperature_window_1D_mean | Temperature_window_1D_max | Temperature_window_1D_min | Temperature_window_7D_mean | Temperature_window_7D_max | Temperature_window_7D_min | Holiday | holiday_previous_day | holiday_next_day | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | ||||||||||||||||||
| 2012-01-08 00:00:00 | 1 | 1 | 6 | 0 | 6 | 21 | 15 | 0 | 20.575 | 24.296875 | 29.0 | 19.875 | 23.254018 | 39.525 | 14.35 | 0 | 0.0 | 0.0 |
| 2012-01-08 01:00:00 | 1 | 1 | 6 | 1 | 6 | 21 | 15 | 0 | 22.500 | 24.098958 | 29.0 | 19.875 | 23.215774 | 39.525 | 14.35 | 0 | 0.0 | 0.0 |
| 2012-01-08 02:00:00 | 1 | 1 | 6 | 2 | 6 | 21 | 15 | 0 | 25.250 | 23.923958 | 29.0 | 19.875 | 23.173214 | 39.525 | 14.35 | 0 | 0.0 | 0.0 |
日历中的某些特征(如小时、天)具有周期性。例如,小时-天的周期为 0 到 23 小时,23:00 实际上距离 00:00 只有一小时。月份-年份同理,12 月距离 1 月也只有一个月。通过正弦和余弦等三角函数变换,可以有效表达周期性模式,避免数据表示上的不连续。这种方法称为周期编码(cyclic encoding),可显著提升模型预测能力。
# 日历和日照特征的周期编码
# ==============================================================================
features_to_encode = [
"month",
"week",
"day_of_week",
"hour",
"sunrise_hour",
"sunset_hour",
]
max_values = {
"month": 12,
"week": 52,
"day_of_week": 6,
"hour": 24,
"sunrise_hour": 24,
"sunset_hour": 24,
}
cyclical_encoder = CyclicalFeatures(
variables = features_to_encode,
max_values = max_values,
drop_original = False
)
exogenous_features = cyclical_encoder.fit_transform(exogenous_features)
exogenous_features.head(3)
| month | week | day_of_week | hour | sunrise_hour | sunset_hour | daylight_hours | is_daylight | Temperature | Temperature_window_1D_mean | ... | week_sin | week_cos | day_of_week_sin | day_of_week_cos | hour_sin | hour_cos | sunrise_hour_sin | sunrise_hour_cos | sunset_hour_sin | sunset_hour_cos | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | |||||||||||||||||||||
| 2012-01-08 00:00:00 | 1 | 1 | 6 | 0 | 6 | 21 | 15 | 0 | 20.575 | 24.296875 | ... | 0.120537 | 0.992709 | -2.449294e-16 | 1.0 | 0.000000 | 1.000000 | 1.0 | 6.123234e-17 | -0.707107 | 0.707107 |
| 2012-01-08 01:00:00 | 1 | 1 | 6 | 1 | 6 | 21 | 15 | 0 | 22.500 | 24.098958 | ... | 0.120537 | 0.992709 | -2.449294e-16 | 1.0 | 0.258819 | 0.965926 | 1.0 | 6.123234e-17 | -0.707107 | 0.707107 |
| 2012-01-08 02:00:00 | 1 | 1 | 6 | 2 | 6 | 21 | 15 | 0 | 25.250 | 23.923958 | ... | 0.120537 | 0.992709 | -2.449294e-16 | 1.0 | 0.500000 | 0.866025 | 1.0 | 6.123234e-17 | -0.707107 | 0.707107 |
3 rows × 30 columns
在许多情况下,外生变量并非孤立影响目标变量,其作用还取决于其他变量的取值。例如,温度对用电需求的影响取决于一天中的时间。变量间的交互作用可通过变量相乘得到新特征,scikit-learn 的 PolynomialFeatures 类可轻松实现。
# 外生变量间的交互作用
# ==============================================================================
transformer_poly = PolynomialFeatures(
degree = 2,
interaction_only = True,
include_bias = False
).set_output(transform="pandas")
poly_cols = [
'month_sin',
'month_cos',
'week_sin',
'week_cos',
'day_of_week_sin',
'day_of_week_cos',
'hour_sin',
'hour_cos',
'sunrise_hour_sin',
'sunrise_hour_cos',
'sunset_hour_sin',
'sunset_hour_cos',
'daylight_hours',
'is_daylight',
'holiday_previous_day',
'holiday_next_day',
'Temperature_window_1D_mean',
'Temperature_window_1D_min',
'Temperature_window_1D_max',
'Temperature_window_7D_mean',
'Temperature_window_7D_min',
'Temperature_window_7D_max',
'Temperature',
'Holiday'
]
poly_features = transformer_poly.fit_transform(exogenous_features[poly_cols])
poly_features = poly_features.drop(columns=poly_cols)
poly_features.columns = [f"poly_{col}" for col in poly_features.columns]
poly_features.columns = poly_features.columns.str.replace(" ", "__")
assert all(poly_features.index == exogenous_features.index)
exogenous_features = pd.concat([exogenous_features, poly_features], axis=1)
exogenous_features.head(3)
| month | week | day_of_week | hour | sunrise_hour | sunset_hour | daylight_hours | is_daylight | Temperature | Temperature_window_1D_mean | ... | poly_Temperature_window_7D_mean__Temperature_window_7D_min | poly_Temperature_window_7D_mean__Temperature_window_7D_max | poly_Temperature_window_7D_mean__Temperature | poly_Temperature_window_7D_mean__Holiday | poly_Temperature_window_7D_min__Temperature_window_7D_max | poly_Temperature_window_7D_min__Temperature | poly_Temperature_window_7D_min__Holiday | poly_Temperature_window_7D_max__Temperature | poly_Temperature_window_7D_max__Holiday | poly_Temperature__Holiday | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | |||||||||||||||||||||
| 2012-01-08 00:00:00 | 1 | 1 | 6 | 0 | 6 | 21 | 15 | 0 | 20.575 | 24.296875 | ... | 333.695156 | 919.115056 | 478.451417 | 0.0 | 567.18375 | 295.25125 | 0.0 | 813.226875 | 0.0 | 0.0 |
| 2012-01-08 01:00:00 | 1 | 1 | 6 | 1 | 6 | 21 | 15 | 0 | 22.500 | 24.098958 | ... | 333.146354 | 917.603460 | 522.354911 | 0.0 | 567.18375 | 322.87500 | 0.0 | 889.312500 | 0.0 | 0.0 |
| 2012-01-08 02:00:00 | 1 | 1 | 6 | 2 | 6 | 21 | 15 | 0 | 25.250 | 23.923958 | ... | 332.535625 | 915.921295 | 585.123661 | 0.0 | 567.18375 | 362.33750 | 0.0 | 998.006250 | 0.0 | 0.0 |
3 rows × 306 columns
# 选择要纳入模型的外生变量
# ==============================================================================
exog_features = []
# 选择以 _sin 或 _cos 结尾的列
exog_features.extend(exogenous_features.filter(regex='_sin$|_cos$').columns.tolist())
# 选择以 temp_ 开头的列
exog_features.extend(exogenous_features.filter(regex='^Temperature_.*').columns.tolist())
# 选择以 holiday_ 开头的列
exog_features.extend(exogenous_features.filter(regex='^Holiday_.*').columns.tolist())
# 包含原始特征
exog_features.extend(['Temperature', 'Holiday'])
# 合并目标变量和外生变量到同一 DataFrame
# ==============================================================================
data = data[['Demand']].merge(
exogenous_features[exog_features],
left_index = True,
right_index = True,
how = 'inner' # 仅使用所有变量均有值的日期
)
data = data.astype('float32')
# 划分数据为 train-val-test
data_train = data.loc[: end_train, :].copy()
data_val = data.loc[end_train:end_validation, :].copy()
data_test = data.loc[end_validation:, :].copy()
再次回测模型,这次将外生变量也作为特征纳入。
# 回测模型
# ==============================================================================
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
exog = data[exog_features],
cv = cv,
metric = 'mean_absolute_error'
)
display(metric)
predictions.head()
| mean_absolute_error | |
|---|---|
| 0 | 141.615022 |
| fold | pred | |
|---|---|---|
| 2014-12-08 00:00:00 | 0 | 4973.909908 |
| 2014-12-08 01:00:00 | 0 | 4976.217860 |
| 2014-12-08 02:00:00 | 0 | 4987.034012 |
| 2014-12-08 03:00:00 | 0 | 5007.016313 |
| 2014-12-08 04:00:00 | 0 | 5027.765102 |
将外生变量作为特征后,模型的预测能力进一步提升。
超参数调优¶
前述 ForecasterRecursive 对象使用了前 24 个滞后和默认超参数的 LGMBRegressor。但这些参数未必最优。为寻找最佳超参数,采用 贝叶斯搜索,通过 bayesian_search_forecaster() 函数实现。搜索过程同样基于回测,每次用不同超参数和滞后组合训练模型。需注意,超参数搜索应在验证集上完成,测试集数据绝不参与。
💡 提示
超参数搜索耗时较长,尤其是基于回测(TimeSeriesFold)的验证策略。更快的替代方案是基于一步预测(OneStepAheadFold)的验证策略。虽然速度更快,但其准确性可能不及回测。详见 回测 vs 一步预测。
# 带间隔的回测
# ==============================================================================
forecaster = ForecasterRecursive(
estimator = LGBMRegressor(random_state=15926, verbose=-1),
lags = 24, # 网格搜索时会被替换
window_features = window_features
)
# 用作特征的滞后
lags_grid = [24, (1, 2, 3, 23, 24, 25, 47, 48, 49)]
# 回归器超参数搜索空间
def search_space(trial):
search_space = {
'n_estimators' : trial.suggest_int('n_estimators', 300, 1000, step=100),
'max_depth' : trial.suggest_int('max_depth', 3, 10),
'learning_rate': trial.suggest_float('learning_rate', 0.01, 0.5),
'reg_alpha' : trial.suggest_float('reg_alpha', 0, 1),
'reg_lambda' : trial.suggest_float('reg_lambda', 0, 1),
'lags' : trial.suggest_categorical('lags', lags_grid)
}
return search_space
# 训练和验证折
cv_search = TimeSeriesFold(
steps = 24,
initial_train_size = len(data[:end_train]),
refit = False,
)
results_search, frozen_trial = bayesian_search_forecaster(
forecaster = forecaster,
y = data.loc[:end_validation, 'Demand'],
exog = data.loc[:end_validation, exog_features],
cv = cv_search,
metric = 'mean_absolute_error',
search_space = search_space,
n_trials = 10, # 增大以获得更全面搜索
return_best = True
)
`Forecaster` refitted using the best-found lags and parameters, and the whole data set:
Lags: [ 1 2 3 23 24 25 47 48 49]
Parameters: {'n_estimators': 800, 'max_depth': 9, 'learning_rate': 0.050765544282894995, 'reg_alpha': 0.7636828414433382, 'reg_lambda': 0.243666374536874}
Backtesting metric: 128.29025410611806
# 搜索结果
# ==============================================================================
best_params = results_search.at[0, 'params']
best_params = best_params | {'random_state': 15926, 'verbose': -1}
best_lags = results_search.at[0, 'lags']
results_search.head(3)
| lags | params | mean_absolute_error | n_estimators | max_depth | learning_rate | reg_alpha | reg_lambda | |
|---|---|---|---|---|---|---|---|---|
| 0 | [1, 2, 3, 23, 24, 25, 47, 48, 49] | {'n_estimators': 800, 'max_depth': 9, 'learnin... | 128.290254 | 800.0 | 9.0 | 0.050766 | 0.763683 | 0.243666 |
| 1 | [1, 2, 3, 23, 24, 25, 47, 48, 49] | {'n_estimators': 800, 'max_depth': 5, 'learnin... | 129.402763 | 800.0 | 5.0 | 0.121157 | 0.551315 | 0.719469 |
| 2 | [1, 2, 3, 23, 24, 25, 47, 48, 49] | {'n_estimators': 600, 'max_depth': 8, 'learnin... | 130.719469 | 600.0 | 8.0 | 0.099421 | 0.175452 | 0.531551 |
由于设置了 return_best=True,预测器对象会自动更新为最佳配置并在全量数据上训练。最终模型可用于新数据的未来预测。
# 最优模型
# ==============================================================================
forecaster
ForecasterRecursive
General Information
- Estimator: LGBMRegressor
- Lags: [ 1 2 3 23 24 25 47 48 49]
- Window features: ['roll_mean_72']
- Window size: 72
- Series name: Demand
- Exogenous included: True
- Weight function included: False
- Differentiation order: None
- Creation date: 2025-11-28 20:50:41
- Last fit date: 2025-11-28 20:52:04
- Skforecast version: 0.19.0
- Python version: 3.13.9
- Forecaster id: None
Exogenous Variables
-
month_sin, month_cos, week_sin, week_cos, day_of_week_sin, day_of_week_cos, hour_sin, hour_cos, sunrise_hour_sin, sunrise_hour_cos, sunset_hour_sin, sunset_hour_cos, poly_month_sin__month_cos, poly_month_sin__week_sin, poly_month_sin__week_cos, poly_month_sin__day_of_week_sin, poly_month_sin__day_of_week_cos, poly_month_sin__hour_sin, poly_month_sin__hour_cos, poly_month_sin__sunrise_hour_sin, poly_month_sin__sunrise_hour_cos, poly_month_sin__sunset_hour_sin, poly_month_sin__sunset_hour_cos, poly_month_cos__week_sin, poly_month_cos__week_cos, ..., poly_day_of_week_cos__sunset_hour_sin, poly_day_of_week_cos__sunset_hour_cos, poly_hour_sin__hour_cos, poly_hour_sin__sunrise_hour_sin, poly_hour_sin__sunrise_hour_cos, poly_hour_sin__sunset_hour_sin, poly_hour_sin__sunset_hour_cos, poly_hour_cos__sunrise_hour_sin, poly_hour_cos__sunrise_hour_cos, poly_hour_cos__sunset_hour_sin, poly_hour_cos__sunset_hour_cos, poly_sunrise_hour_sin__sunrise_hour_cos, poly_sunrise_hour_sin__sunset_hour_sin, poly_sunrise_hour_sin__sunset_hour_cos, poly_sunrise_hour_cos__sunset_hour_sin, poly_sunrise_hour_cos__sunset_hour_cos, poly_sunset_hour_sin__sunset_hour_cos, Temperature_window_1D_mean, Temperature_window_1D_max, Temperature_window_1D_min, Temperature_window_7D_mean, Temperature_window_7D_max, Temperature_window_7D_min, Temperature, Holiday
Data Transformations
- Transformer for y: None
- Transformer for exog: None
Training Information
- Training range: [Timestamp('2012-01-08 00:00:00'), Timestamp('2014-11-30 23:00:00')]
- Training index type: DatetimeIndex
- Training index frequency:
Estimator Parameters
-
{'boosting_type': 'gbdt', 'class_weight': None, 'colsample_bytree': 1.0, 'importance_type': 'split', 'learning_rate': 0.050765544282894995, 'max_depth': 9, 'min_child_samples': 20, 'min_child_weight': 0.001, 'min_split_gain': 0.0, 'n_estimators': 800, 'n_jobs': None, 'num_leaves': 31, 'objective': None, 'random_state': 15926, 'reg_alpha': 0.7636828414433382, 'reg_lambda': 0.243666374536874, 'subsample': 1.0, 'subsample_for_bin': 200000, 'subsample_freq': 0, 'verbose': -1}
Fit Kwargs
-
{}
确定最佳超参数组合(基于验证集)后,评估模型在测试集上的预测能力。
# 在测试集上回测最终模型
# ==============================================================================
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
exog = data[exog_features],
cv = cv,
metric = 'mean_absolute_error'
)
display(metric)
predictions.head()
| mean_absolute_error | |
|---|---|
| 0 | 132.742342 |
| fold | pred | |
|---|---|---|
| 2014-12-08 00:00:00 | 0 | 4975.449681 |
| 2014-12-08 01:00:00 | 0 | 5002.267029 |
| 2014-12-08 02:00:00 | 0 | 5025.141643 |
| 2014-12-08 03:00:00 | 0 | 5057.270548 |
| 2014-12-08 04:00:00 | 0 | 5087.195752 |
经过滞后和超参数优化后,预测误差进一步降低。
特征选择¶
特征选择是从所有特征中选出最相关子集用于建模的重要步骤,有助于减少过拟合、提升模型精度并缩短训练时间。skforecast 的底层回归器遵循 scikit-learn API,因此可直接用 select_features() 函数结合 scikit-learn 的特征选择方法。最常用的两种方法为 递归特征消除 和 顺序特征选择。
💡 提示
特征选择是提升机器学习模型性能的有力工具,但计算量大且耗时。目标是找到最佳特征子集,而非最优模型,因此可用较小数据子集和简单模型。确定最佳特征后,再用全量数据和更复杂配置训练模型。
# 创建预测器
# ==============================================================================
estimator = LGBMRegressor(
n_estimators = 100,
max_depth = 4,
random_state = 15926,
verbose = -1
)
forecaster = ForecasterRecursive(
estimator = estimator,
lags = best_lags,
window_features = window_features
)
# 递归特征消除与交叉验证
# ==============================================================================
warnings.filterwarnings("ignore", message="X does not have valid feature names.*")
selector = RFECV(
estimator = estimator,
step = 1,
cv = 3,
)
lags_select, window_features_select, exog_select = select_features(
forecaster = forecaster,
selector = selector,
y = data_train['Demand'],
exog = data_train[exog_features],
select_only = None,
force_inclusion = None,
subsample = 0.5, # 加速过程
random_state = 123,
verbose = True,
)
Recursive feature elimination (RFECV)
-------------------------------------
Total number of records available: 17304
Total number of records used for feature selection: 8652
Number of features available: 96
Lags (n=9)
Window features (n=1)
Exog (n=86)
Number of features selected: 45
Lags (n=9) : [1, 2, 3, 23, 24, 25, 47, 48, 49]
Window features (n=1) : ['roll_mean_72']
Exog (n=35) : ['week_cos', 'hour_sin', 'hour_cos', 'poly_month_sin__day_of_week_cos', 'poly_month_sin__hour_cos', 'poly_month_cos__hour_cos', 'poly_week_sin__hour_sin', 'poly_week_sin__hour_cos', 'poly_week_cos__day_of_week_sin', 'poly_week_cos__day_of_week_cos', 'poly_week_cos__hour_sin', 'poly_week_cos__hour_cos', 'poly_day_of_week_sin__day_of_week_cos', 'poly_day_of_week_sin__hour_sin', 'poly_day_of_week_sin__hour_cos', 'poly_day_of_week_sin__sunrise_hour_sin', 'poly_day_of_week_cos__hour_sin', 'poly_day_of_week_cos__hour_cos', 'poly_day_of_week_cos__sunrise_hour_cos', 'poly_hour_sin__hour_cos', 'poly_hour_sin__sunrise_hour_cos', 'poly_hour_sin__sunset_hour_sin', 'poly_hour_sin__sunset_hour_cos', 'poly_hour_cos__sunrise_hour_sin', 'poly_hour_cos__sunrise_hour_cos', 'poly_hour_cos__sunset_hour_sin', 'poly_hour_cos__sunset_hour_cos', 'Temperature_window_1D_mean', 'Temperature_window_1D_max', 'Temperature_window_1D_min', 'Temperature_window_7D_mean', 'Temperature_window_7D_max', 'Temperature_window_7D_min', 'Temperature', 'Holiday']
Scikit-learn 的 RFECV 首先用全部特征训练模型,获取每个特征的重要性(如 coef_ 或 feature_importances_)。随后每轮迭代剔除最不重要特征,并通过交叉验证评估剩余特征的模型性能。该过程持续,直到移除特征不再提升或开始降低模型性能(基于选定指标),或达到 min_features_to_select。
最终结果是通过交叉验证获得的、在模型简洁性与预测能力间取得最佳平衡的特征子集。
用最佳特征子集重新训练并评估预测器。
# 用选定特征创建预测器
# ==============================================================================
forecaster = ForecasterRecursive(
estimator = LGBMRegressor(**best_params),
lags = lags_select,
window_features = window_features
)
# 在验证数据上进行回测以获得样本外残差
# ==============================================================================
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
exog = data[exog_select],
cv = cv,
metric = 'mean_absolute_error'
)
metric
| mean_absolute_error | |
|---|---|
| 0 | 131.391247 |
在不损失模型性能的前提下减少了特征数量,使模型更简洁、训练更快,也降低了过拟合风险。
概率性预测:预测区间¶
预测区间定义了目标变量真实值在给定概率下可能出现的区间。Skforecast 实现了多种概率性预测方法:
以下代码展示如何为自回归模型生成预测区间。prediction_interval() 函数可为每个预测步生成区间。backtesting_forecaster() 可为整个测试集生成区间。interval 参数指定区间的置信概率,本例设置为 [5, 95],即计算 5% 和 95% 分位数的区间,对应理论覆盖率 90%。
# 创建并训练预测器
# ==============================================================================
forecaster = ForecasterRecursive(
estimator = LGBMRegressor(**best_params),
lags = lags_select,
window_features = window_features,
binner_kwargs = {"n_bins": 5}
)
forecaster.fit(
y = data.loc[:end_train, 'Demand'],
exog = data.loc[:end_train, exog_select],
store_in_sample_residuals = True
)
# 预测区间
# ==============================================================================
# 由于模型已使用外生变量进行训练,因此在预测时也必须提供外生变量。
predictions = forecaster.predict_interval(
exog = data.loc[end_train:, exog_select],
steps = 24,
interval = [5, 95],
method = 'conformal',
)
predictions.head()
| pred | lower_bound | upper_bound | |
|---|---|---|---|
| 2014-01-01 00:00:00 | 3659.284654 | 3619.432029 | 3699.137278 |
| 2014-01-01 01:00:00 | 3809.478172 | 3769.625548 | 3849.330797 |
| 2014-01-01 02:00:00 | 3941.153515 | 3895.670015 | 3986.637016 |
| 2014-01-01 03:00:00 | 3973.933981 | 3928.450480 | 4019.417482 |
| 2014-01-01 04:00:00 | 4062.377324 | 4016.893823 | 4107.860824 |
默认情况下,区间基于样本内残差(训练集残差)计算。但这样得到的区间可能过窄(过于乐观)。为避免此问题,可用 set_out_sample_residuals() 方法指定通过回测在验证集上计算的样本外残差。
如果在 set_out_sample_residuals() 中同时传入预测值,则自助法采样残差时可按预测值区间分组,有助于提升区间覆盖率并尽量缩小区间宽度。
# 在验证数据上进行回测以获得样本外残差
# ==============================================================================
cv = TimeSeriesFold(
steps = 24,
initial_train_size = len(data.loc[:end_train]),
refit = False,
)
_, predictions_val = backtesting_forecaster(
forecaster = forecaster,
y = data.loc[:end_validation, 'Demand'],
exog = data.loc[:end_validation, exog_select],
cv = cv,
metric = 'mean_absolute_error'
)
# 样本外残差分布
# ==============================================================================
residuals = data.loc[predictions_val.index, 'Demand'] - predictions_val['pred']
print(pd.Series(np.where(residuals < 0, 'negative', 'positive')).value_counts())
plt.rcParams.update({'font.size': 8})
_ = plot_residuals(residuals=residuals, figsize=(7, 4))
negative 4429 positive 3587 Name: count, dtype: int64
# 在预测器中存储样本外残差
# ==============================================================================
forecaster.set_out_sample_residuals(
y_true = data.loc[predictions_val.index, 'Demand'],
y_pred = predictions_val['pred']
)
随后在测试集上运行 回测,以估算预测区间。use_in_sample_residuals 设为 False,以使用前面存储的样本外残差,use_binned_residuals 设为 True,使自助法采样残差时按预测值区间分组。
# 在测试数据中使用样本外残差进行区间预测的回测
# ==============================================================================
cv = TimeSeriesFold(
steps = 24,
initial_train_size = len(data.loc[:end_validation]),
refit = False,
)
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
exog = data[exog_select],
cv = cv,
metric = 'mean_absolute_error',
interval = [5, 95],
interval_method = 'conformal',
use_in_sample_residuals = False, # 样本外残差
use_binned_residuals = True, # 区间根据预测值分组
)
predictions.head(5)
| fold | pred | lower_bound | upper_bound | |
|---|---|---|---|---|
| 2014-12-01 00:00:00 | 0 | 5609.728357 | 5141.917122 | 6077.539593 |
| 2014-12-01 01:00:00 | 0 | 5570.278476 | 5102.467241 | 6038.089711 |
| 2014-12-01 02:00:00 | 0 | 5557.446741 | 5089.635506 | 6025.257976 |
| 2014-12-01 03:00:00 | 0 | 5574.087926 | 5106.276691 | 6041.899161 |
| 2014-12-01 04:00:00 | 0 | 5655.740166 | 5187.928931 | 6123.551402 |
# 绘制预测区间与真实值对比图
# ==============================================================================
fig = go.Figure([
go.Scatter(
name='Prediction', x=predictions.index, y=predictions['pred'], mode='lines',
),
go.Scatter(
name='Real value', x=data_test.index, y=data_test['Demand'], mode='lines',
),
go.Scatter(
name='Upper Bound', x=predictions.index, y=predictions['upper_bound'],
mode='lines', marker=dict(color="#444"), line=dict(width=0), showlegend=False
),
go.Scatter(
name='Lower Bound', x=predictions.index, y=predictions['lower_bound'],
marker=dict(color="#444"), line=dict(width=0), mode='lines',
fillcolor='rgba(68, 68, 68, 0.3)', fill='tonexty', showlegend=False
)
])
fig.update_layout(
title="Real value vs predicted in test data",
xaxis_title="Date time",
yaxis_title="Demand",
width=800,
height=400,
margin=dict(l=20, r=20, t=35, b=20),
hovermode="x",
legend=dict(orientation="h", yanchor="top", y=1.1, xanchor="left", x=0.001)
)
fig.show()
# 预测区间覆盖率(测试数据)
# ==============================================================================
coverage = calculate_coverage(
y_true = data.loc[end_validation:, "Demand"],
lower_bound = predictions["lower_bound"],
upper_bound = predictions["upper_bound"]
)
area = (predictions['upper_bound'] - predictions['lower_bound']).sum()
print(f"Total area of the interval: {round(area, 2)}")
print(f"Predicted interval coverage: {round(100 * coverage, 2)} %")
Total area of the interval: 335515.26 Predicted interval coverage: 86.64 %
区间的实际覆盖率接近理论期望覆盖率(90%)。
✏️ 注意
关于 skforecast 概率性预测功能的详细说明,请参见:机器学习概率性预测。
模型可解释性与可解释性¶
许多现代机器学习模型(如集成方法)本质上是黑盒,难以理解其具体预测原因。可解释性技术旨在揭示模型内部机制,提升透明度、建立信任,并满足各领域的合规需求。提升模型可解释性不仅有助于理解模型行为,还能识别偏差、提升性能,并帮助利益相关者基于机器学习洞见做出更明智决策。
skforecast 兼容多种主流模型可解释性方法:模型特定特征重要性、SHAP 值、部分依赖图。
# 创建并训练预测器
# ==============================================================================
forecaster = ForecasterRecursive(
estimator = LGBMRegressor(**best_params),
lags = lags_select,
window_features = window_features
)
forecaster.fit(
y = data.loc[:end_validation, 'Demand'],
exog = data.loc[:end_validation, exog_select]
)
模型特定特征重要性¶
# 模型特定的特征重要性
# ==============================================================================
feature_importances = forecaster.get_feature_importances()
feature_importances.head(10)
| feature | importance | |
|---|---|---|
| 0 | lag_1 | 2279 |
| 43 | Temperature | 1285 |
| 1 | lag_2 | 1167 |
| 5 | lag_25 | 1111 |
| 2 | lag_3 | 1047 |
| 4 | lag_24 | 975 |
| 3 | lag_23 | 757 |
| 39 | Temperature_window_1D_min | 713 |
| 38 | Temperature_window_1D_max | 689 |
| 29 | poly_hour_sin__hour_cos | 683 |
⚠️ 警告
只有当预测器的回归器具有 coef_ 或 feature_importances_ 属性(scikit-learn 默认支持)时,get_feature_importances() 方法才会返回结果。
Shap 值¶
SHAP(SHapley Additive exPlanations)是一种基于博弈论的解释方法,用于量化每个特征对单个预测的贡献。SHAP 值可以帮助我们理解模型为何做出某个特定预测。
# 由预测器用于拟合内部回归器的训练矩阵
# ==============================================================================
X_train, y_train = forecaster.create_train_X_y(
y = data_train['Demand'],
exog = data_train[exog_select]
)
display(X_train.head(3))
display(y_train.head(3))
| lag_1 | lag_2 | lag_3 | lag_23 | lag_24 | lag_25 | lag_47 | lag_48 | lag_49 | roll_mean_72 | ... | poly_hour_cos__sunset_hour_sin | poly_hour_cos__sunset_hour_cos | Temperature_window_1D_mean | Temperature_window_1D_max | Temperature_window_1D_min | Temperature_window_7D_mean | Temperature_window_7D_max | Temperature_window_7D_min | Temperature | Holiday | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | |||||||||||||||||||||
| 2012-01-11 00:00:00 | 5087.274902 | 4925.770996 | 4661.530762 | 4988.975098 | 4963.185059 | 4896.571289 | 5039.643066 | 4958.630371 | 4886.074219 | 4386.356154 | ... | -0.707107 | 0.707107 | 16.140625 | 19.575001 | 13.175 | 19.321875 | 29.0 | 13.175 | 15.150 | 0.0 |
| 2012-01-11 01:00:00 | 5107.675781 | 5087.274902 | 4925.770996 | 5006.663086 | 4988.975098 | 4963.185059 | 5090.203125 | 5039.643066 | 4958.630371 | 4398.891398 | ... | -0.683013 | 0.683013 | 16.042707 | 19.575001 | 13.175 | 19.291666 | 29.0 | 13.175 | 15.425 | 0.0 |
| 2012-01-11 02:00:00 | 5126.337891 | 5107.675781 | 5087.274902 | 4977.723633 | 5006.663086 | 4988.975098 | 5108.837402 | 5090.203125 | 5039.643066 | 4410.526191 | ... | -0.612372 | 0.612372 | 15.939584 | 19.575001 | 13.175 | 19.255507 | 29.0 | 13.175 | 14.800 | 0.0 |
3 rows × 45 columns
Time 2012-01-11 00:00:00 5107.675781 2012-01-11 01:00:00 5126.337891 2012-01-11 02:00:00 5103.370605 Freq: h, Name: y, dtype: float32
# 创建 SHAP 解释器(针对三个基模型)
# ==============================================================================
shap.initjs()
explainer = shap.TreeExplainer(forecaster.estimator)
# 抽取 50% 的数据以加快计算
# ==============================================================================
rng = np.random.default_rng(seed=785412)
sample = rng.choice(X_train.index, size=int(len(X_train)*0.5), replace=False)
X_train_sample = X_train.loc[sample, :]
shap_values = explainer.shap_values(X_train_sample)
结论¶
# SHAP 摘要图(前 10 个特征)
# ==============================================================================
shap.summary_plot(shap_values, X_train_sample, max_display=10, show=False)
fig, ax = plt.gcf(), plt.gca()
ax.set_title("SHAP Summary plot")
ax.tick_params(labelsize=8)
fig.set_size_inches(6, 4.5)
在本教程中,我们展示了如何使用 skforecast 和 LightGBM 对电力需求进行时间序列预测。我们涵盖了数据预处理、特征工程、模型训练、回测、概率性预测以及模型可解释性等关键步骤。
skforecast 提供了灵活且强大的工具,能够轻松实现和评估多种机器学习模型在时间序列预测中的表现。
# 回测并返回预测器
# ==============================================================================
cv = TimeSeriesFold(
steps = 24,
initial_train_size = len(data.loc[:end_validation]),
)
_, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
exog = data[exog_select],
cv = cv,
metric = 'mean_absolute_error',
return_predictors = True,
)
会话信息¶
predictions.head(3)
| fold | pred | lag_1 | lag_2 | lag_3 | lag_23 | lag_24 | lag_25 | lag_47 | lag_48 | ... | poly_hour_cos__sunset_hour_sin | poly_hour_cos__sunset_hour_cos | Temperature_window_1D_mean | Temperature_window_1D_max | Temperature_window_1D_min | Temperature_window_7D_mean | Temperature_window_7D_max | Temperature_window_7D_min | Temperature | Holiday | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2014-12-01 00:00:00 | 0 | 5609.728357 | 5634.690430 | 5519.464844 | 5250.484863 | 4326.276855 | 4102.013672 | 3851.330322 | 4056.273926 | 4058.317627 | ... | -0.866025 | 0.500000 | 28.779167 | 33.849998 | 23.6 | 18.208036 | 33.849998 | 11.15 | 20.000000 | 0.0 |
| 2014-12-01 01:00:00 | 0 | 5570.278476 | 5609.728357 | 5634.690430 | 5519.464844 | 4560.871094 | 4326.276855 | 4102.013672 | 4060.130127 | 4056.273926 | ... | -0.836516 | 0.482963 | 28.556250 | 33.849998 | 20.0 | 18.224703 | 33.849998 | 11.15 | 20.350000 | 0.0 |
| 2014-12-01 02:00:00 | 0 | 5557.446741 | 5570.278476 | 5609.728357 | 5634.690430 | 4782.341309 | 4560.871094 | 4326.276855 | 4071.491943 | 4060.130127 | ... | -0.750000 | 0.433013 | 28.193750 | 33.849998 | 20.0 | 18.242857 | 33.849998 | 11.15 | 22.299999 | 0.0 |
3 rows × 47 columns
# 回测期间生成的单个预测的瀑布图
# ==============================================================================
predictions = predictions.astype(data[exog_select].dtypes) # 确保类型一致
iloc_predicted_date = predictions.index.get_loc('2014-12-16 12:00:00')
shap_values_single = explainer(predictions.iloc[:, 2:])
shap.plots.waterfall(shap_values_single[iloc_predicted_date], show=False)
fig, ax = plt.gcf(), plt.gca()
fig.set_size_inches(8, 3.5)
ax_list = fig.axes
ax = ax_list[0]
ax.tick_params(labelsize=8)
ax.set
plt.show()
# 回测期间生成的单个预测的力图
# ==============================================================================
shap.force_plot(
base_value = shap_values_single.base_values[iloc_predicted_date],
shap_values = shap_values_single.values[iloc_predicted_date],
features = predictions.iloc[iloc_predicted_date, 2:],
)
Have you run `initjs()` in this notebook? If this notebook was from another user you must also trust this notebook (File -> Trust notebook). If you are viewing this notebook on github the Javascript has been stripped for security. If you are using JupyterLab this error is because a JupyterLab extension has not yet been written.
引用¶
ForecasterRecursive 和 ForecasterRecursiveCustom 模型采用递归策略,即每一个新的预测都基于前一个预测结果。另一种多步预测策略是为每一个需要预测的步长分别训练一个模型,这被称为直接多步预测。虽然由于需要训练多个模型,这种方法在计算上比递归方法更昂贵,但它可能带来更好的结果。
# 直接法预测器
# ==============================================================================
forecaster = ForecasterDirect(
estimator = LGBMRegressor(**best_params),
steps = 24,
lags = lags_select,
window_features = window_features
)
# 回测模型
# ==============================================================================
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
exog = data[exog_select],
cv = cv,
metric = 'mean_absolute_error'
)
display(metric)
predictions.head()
| mean_absolute_error | |
|---|---|
| 0 | 119.096333 |
| fold | pred | |
|---|---|---|
| 2014-12-01 00:00:00 | 0 | 5643.441883 |
| 2014-12-01 01:00:00 | 0 | 5770.005014 |
| 2014-12-01 02:00:00 | 0 | 5844.018982 |
| 2014-12-01 03:00:00 | 0 | 6144.759526 |
| 2014-12-01 04:00:00 | 0 | 6105.915435 |
如需更多信息,请访问 skforecast 官方文档。
预期的每日预测¶
到目前为止,我们假设每天的次日预测是在当天晚上 11:59 生成的。但这种做法在实际中并不现实,因为没有时间处理第二天的凌晨时段。
现在,假设每天需要在上午 11:00 生成次日的预测,以便有足够的时间进行管理。这意味着在第 $D$ 天的 11:00,你需要预测当天 [12, 13, ..., 23] 点和第 $D+1$ 天的 [0, 1, ..., 23] 点,共 36 小时的需求(但只需保留最后 24 小时的预测结果)。
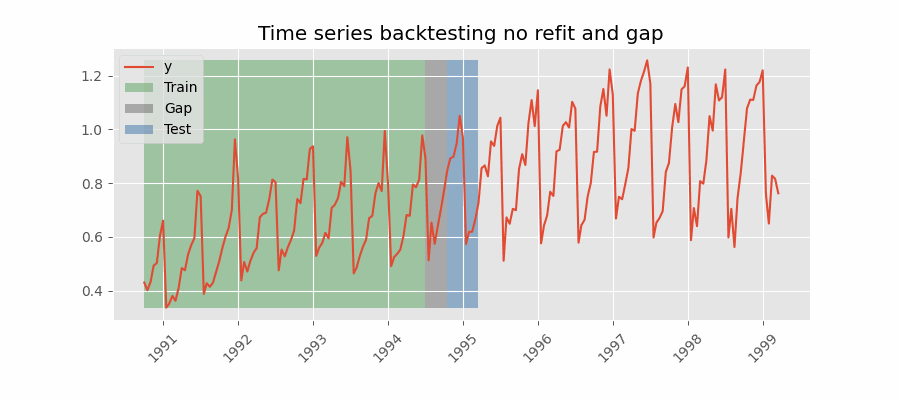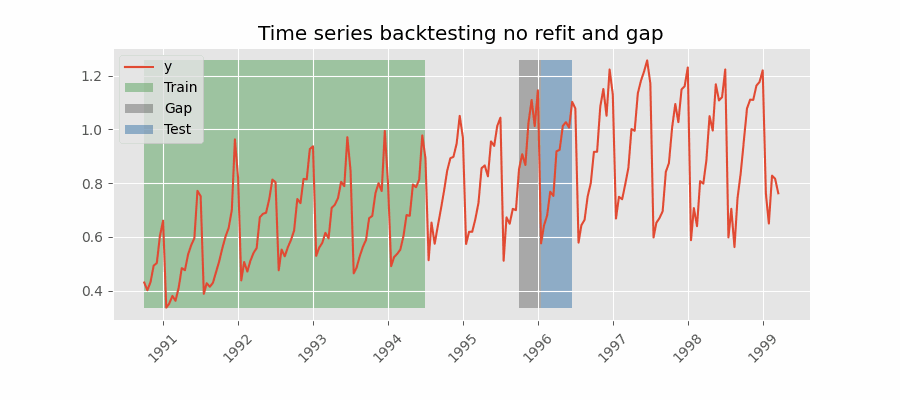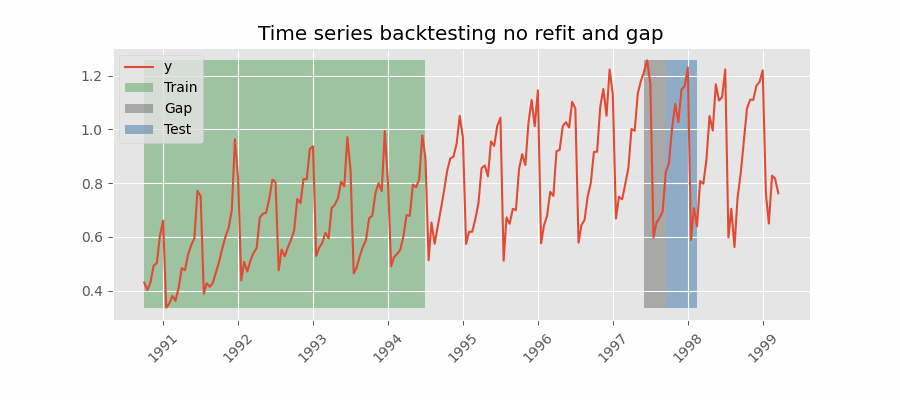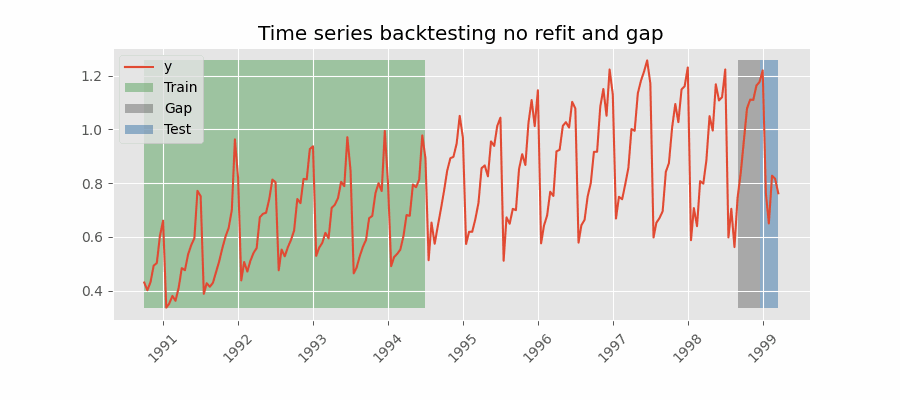
这种评估方式可以通过 backtesting_forecaster() 函数及其 gap 参数轻松实现。此外,allow_incomplete_fold 参数允许在最后一个分组不满足步数要求时将其排除。该流程每天运行一次,步骤如下:
- 在测试集的第一天上午 11:00,预测接下来 36 小时(当天剩余 12 小时加上次日 24 小时)。
- 只保留次日的预测(从位置 12 开始)。
- 将次日 11:00 前的数据加入测试集。
- 重复该过程。
因此,每天上午 11:00,模型都能访问到截至该时刻的真实需求值。
⚠️ 注意
有两个注意事项:
- 训练数据必须在 gap 开始处结束。本例中,
initial_train_size需多加 12 个位置,使第一个预测点为 2014-12-01 12:00:00。 - 虽然每次只保留最后 24 个预测(steps)用于模型评估,但每个分组实际预测的步数为 36(steps + gap)。
# initial_train_size + 12 位置的末尾
# ==============================================================================
data.iloc[:len(data.loc[:end_validation]) + 12].tail(2)
| Demand | month_sin | month_cos | week_sin | week_cos | day_of_week_sin | day_of_week_cos | hour_sin | hour_cos | sunrise_hour_sin | ... | poly_sunrise_hour_cos__sunset_hour_cos | poly_sunset_hour_sin__sunset_hour_cos | Temperature_window_1D_mean | Temperature_window_1D_max | Temperature_window_1D_min | Temperature_window_7D_mean | Temperature_window_7D_max | Temperature_window_7D_min | Temperature | Holiday | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | |||||||||||||||||||||
| 2014-12-01 10:00:00 | 5084.011230 | -2.449294e-16 | 1.0 | -0.354605 | 0.935016 | 0.0 | 1.0 | 0.500000 | -0.866025 | 1.0 | ... | 3.061617e-17 | -0.433013 | 25.589582 | 30.950001 | 20.0 | 18.573214 | 33.849998 | 11.15 | 19.90 | 0.0 |
| 2014-12-01 11:00:00 | 4851.066895 | -2.449294e-16 | 1.0 | -0.354605 | 0.935016 | 0.0 | 1.0 | 0.258819 | -0.965926 | 1.0 | ... | 3.061617e-17 | -0.433013 | 25.129168 | 29.500000 | 19.9 | 18.601191 | 33.849998 | 11.15 | 19.35 | 0.0 |
2 rows × 87 columns
# 预测器
# ==============================================================================
forecaster = ForecasterRecursive(
estimator = LGBMRegressor(**best_params),
lags = lags_select,
window_features = window_features
)
# 带间隔的回测
# ==============================================================================
cv = TimeSeriesFold(
steps = 24,
initial_train_size = len(data.loc[:end_validation]) + 12,
refit = False,
gap = 12,
)
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
exog = data[exog_select],
cv = cv,
metric = 'mean_absolute_error'
)
display(metric)
predictions.head(5)
| mean_absolute_error | |
|---|---|
| 0 | 138.496187 |
| fold | pred | |
|---|---|---|
| 2014-12-02 00:00:00 | 0 | 5459.348705 |
| 2014-12-02 01:00:00 | 0 | 5506.327848 |
| 2014-12-02 02:00:00 | 0 | 5590.533606 |
| 2014-12-02 03:00:00 | 0 | 5688.215164 |
| 2014-12-02 04:00:00 | 0 | 5835.673206 |
如预期,随着预测时长从 24 小时增加到 36 小时,误差也随之增加。
结论¶
梯度提升模型已被证明是预测能源需求的强大工具。其主要优势之一在于能够轻松引入外生变量,从而显著提升模型的预测能力。此外,借助可解释性技术,可以直观且定量地理解变量及其取值对预测的影响。所有这些问题都可以通过 skforecast 库轻松解决。
| 预测器类型 | 外生变量 | MAE 回测 |
|---|---|---|
ForecasterEquivalentDate (基线) |
否 | 308.4 |
ForecasterRecursive |
否 | 225.5 |
ForecasterRecursive |
是 | 132.7 |
ForecasterRecursive |
是(特征选择) | 131.9 |
ForecasterDirect |
是(特征选择) | 119.1 |
会话信息¶
import session_info
session_info.show(html=False)
----- astral 3.2 feature_engine 1.9.3 lightgbm 4.6.0 matplotlib 3.10.8 numpy 2.3.4 optuna 4.6.0 pandas 2.3.3 plotly 6.4.0 session_info v1.0.1 shap 0.50.0 skforecast 0.19.0 sklearn 1.7.2 statsmodels 0.14.5 ----- IPython 9.7.0 jupyter_client 8.6.3 jupyter_core 5.9.1 ----- Python 3.13.9 | packaged by conda-forge | (main, Oct 22 2025, 23:12:41) [MSC v.1944 64 bit (AMD64)] Windows-11-10.0.26100-SP0 ----- Session information updated at 2025-11-28 20:53
引用¶
如何引用本文档
如果你使用了本文档或其中的任何部分,请注明来源,谢谢!
《使用机器学习预测能源需求》作者:Joaquín Amat Rodrigo 和 Javier Escobar Ortiz,遵循 Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0 DEED) 许可,原文链接:https://www.cienciadedatos.net/documentos/py29-forecasting-electricity-power-demand-python.html
如何引用 skforecast
如果你在论文或出版物中使用了 skforecast,欢迎引用已发布的软件。
Zenodo:
Amat Rodrigo, Joaquin, & Escobar Ortiz, Javier. (2024). skforecast (v0.17.0). Zenodo. https://doi.org/10.5281/zenodo.8382788
APA:
Amat Rodrigo, J., & Escobar Ortiz, J. (2024). skforecast (Version 0.17.0) [计算机软件]. https://doi.org/10.5281/zenodo.8382788
BibTeX:
@software{skforecast, author = {Amat Rodrigo, Joaquin and Escobar Ortiz, Javier}, title = {skforecast}, version = {0.17.0}, month = {08}, year = {2025}, license = {BSD-3-Clause}, url = {https://skforecast.org/}, doi = {10.5281/zenodo.8382788} }
喜欢这篇文章吗?你的支持很重要
你的支持将帮助我持续创作免费教育内容,感谢!😊
本作品由 Joaquín Amat Rodrigo 和 Javier Escobar Ortiz 创作,采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议。
允许:
-
共享:可以以任何媒介或格式复制、传播本材料。
-
演绎:可以对本材料进行再混合、转换和创作。
须遵守以下条款:


