More about forecasting in cienciadedatos.net

• ARIMA and SARIMAX models with python
• Time series forecasting with machine learning
• Forecasting time series with gradient boosting: XGBoost, LightGBM and CatBoost
• Forecasting time series with XGBoost
• Global Forecasting Models: Multi-series forecasting
• Global Forecasting Models: Comparative Analysis of Single and Multi-Series Forecasting Modeling
• Probabilistic forecasting
• Forecasting with deep learning
• Forecasting energy demand with machine learning
• Forecasting web traffic with machine learning
• Intermittent demand forecasting
• Modelling time series trend with tree-based models
• Bitcoin price prediction with Python
• Stacking ensemble of machine learning models to improve forecasting
• Interpretable forecasting models
• Mitigating the Impact of Covid on forecasting Models
• Forecasting time series with missing values

Introduction¶

Energy demand forecasting plays a critical role in effectively managing and planning resources for power generation, distribution, and utilization. Predicting energy demand is a complex task influenced by factors such as weather patterns, economic conditions, and societal behavior. This document will examine the creation of forecasting models utilizing machine learning to predict energy demand.

Time series and forecasting

A time series is a sequence of chronologically ordered data at equal or unequal intervals. The forecasting process consists of predicting the future value of a time series, either by modelling the series solely on the basis of its past behavior (autoregressive) or by using other external variables.

When working with time series, it is rarely necessary to predict only the next element in the series ($t_{+1}$). Instead, the most common goal is to forecast a whole future interval (($t_{+1}$), ..., ($t_{+n}$)) or a far future time ($t_{+n}$). Several strategies can be used to generate this type of forecast, skforecast has implemented the following for univariate time series forecasting:

• Recursive multi-step forecasting: since the value $t_{n-1}$ is needed to predict $t_{n}$, and $t_{n-1}$ is unknown, a recursive process is applied in which each new prediction is based on the previous one. This process is known as recursive forecasting or recursive multi-step forecasting and can be easily generated with the ForecasterRecursive class.

• Direct multi-step forecasting: this method consists of training a different model for each step of the forecast horizon. For example, to predict the next 5 values of a time series, 5 different models are trained, one for each step. As a result, the predictions are independent of each other. This entire process is automated in the ForecasterDirect class.

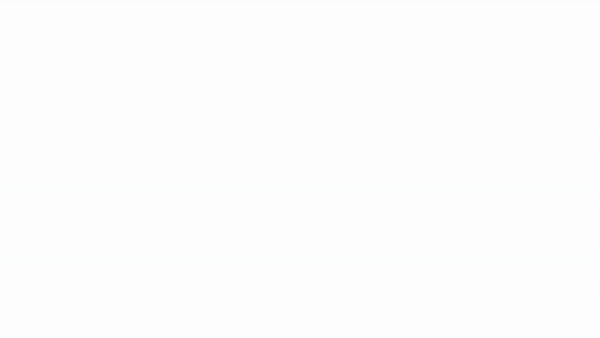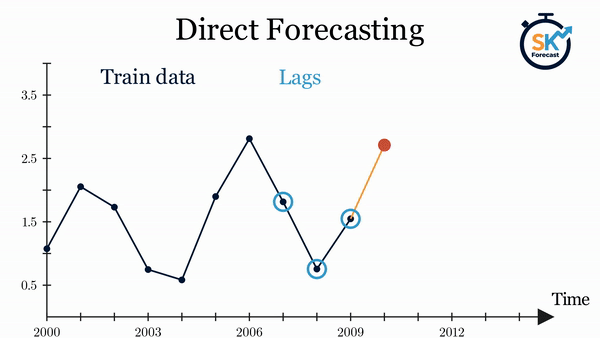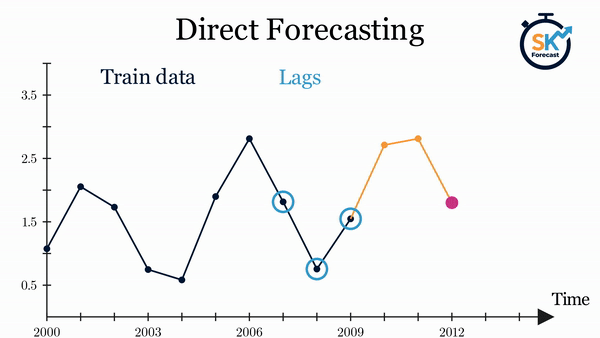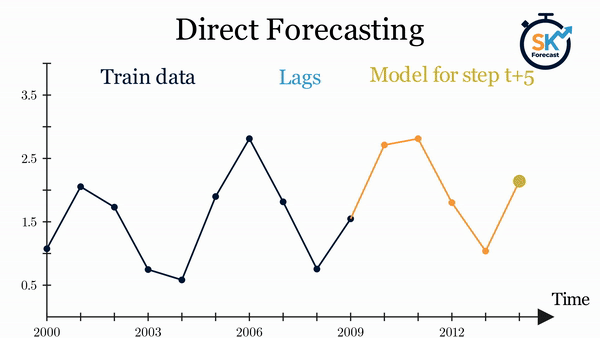
• Multi-output forecasting: Some machine learning models, such as long short-term memory (LSTM) neural networks, can predict multiple values of a sequence simultaneously (one-shot). This strategy is implemented in the ForecasterRnn class.

Libraries¶

The libraries used in this document are:

# Data manipulation
# ==============================================================================
import numpy as np
import pandas as pd
from astral.sun import sun
from astral import LocationInfo
from skforecast.datasets import fetch_dataset

# Plots
# ==============================================================================
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from skforecast.plot import plot_residuals
import plotly.graph_objects as go
import plotly.io as pio
import plotly.offline as poff
pio.templates.default = 'seaborn'
poff.init_notebook_mode(connected=True)
plt.style.use('seaborn-v0_8-darkgrid')
plt.rcParams.update({'font.size': 8})

# Modelling and Forecasting
# ==============================================================================
import skforecast
import lightgbm
import sklearn
from lightgbm import LGBMRegressor
from sklearn.preprocessing import PolynomialFeatures
from sklearn.feature_selection import RFECV
from feature_engine.timeseries.forecasting import WindowFeatures
from skforecast.preprocessing import CalendarFeatures, RollingFeatures
from skforecast.recursive import ForecasterEquivalentDate, ForecasterRecursive
from skforecast.direct import ForecasterDirect
from skforecast.model_selection import (
    TimeSeriesFold,
    bayesian_search_forecaster,
    backtesting_forecaster
)
from skforecast.feature_selection import select_features
from skforecast.stats import calculate_lag_autocorrelation
from skforecast.metrics import calculate_coverage
import shap

# Warnings configuration
# ==============================================================================
import warnings
warnings.filterwarnings('once')

color = '\033[1m\033[38;5;208m'
print(f'{color}Version skforecast: {skforecast.__version__}')
print(f'{color}Version scikit-learn: {sklearn.__version__}')
print(f'{color}Version lightgbm: {lightgbm.__version__}')
print(f'{color}Version pandas: {pd.__version__}')
print(f'{color}Version numpy: {np.__version__}')

Version skforecast: 0.25.0
Version scikit-learn: 1.7.2
Version lightgbm: 4.7.0
Version pandas: 2.3.3
Version numpy: 2.4.6

Data¶

A time series of electricity demand (MW) is available for the state of Victoria (Australia) from 2012-01-01 to 2014-12-31. The data used in this document has been obtained from the R tsibbledata package. The dataset contains 5 columns and 52,608 complete records. The information in each column is:

• Time: date and time of the record (stored in UTC).
• Date: date of the record.
• Demand: electricity demand (MW).
• Temperature: temperature in Melbourne, the capital of Victoria.
• Holiday: indicates if the day is a public holiday.

Note on units and aggregation: The source tsibbledata package labels Demand as "MWh", but the values are actually average power in MW (average operational demand over each 30-minute interval). This is why the hourly series is built with mean rather than sum: averaging two consecutive 30-minute power readings gives the average hourly power (MW), which is numerically identical to the hourly energy (MWh over a 1-hour window). Summing would double the values and produce a series with no valid physical interpretation.

# Data download
# ==============================================================================
data = fetch_dataset(name='vic_electricity', raw=True)
data.info()

╭──────────────────────────── vic_electricity ─────────────────────────────╮
│ Description:                                                             │
│ Half-hourly electricity demand for Victoria, Australia                   │
│                                                                          │
│ Source:                                                                  │
│ O'Hara-Wild M, Hyndman R, Wang E, Godahewa R (2022).tsibbledata: Diverse │
│ Datasets for 'tsibble'. https://tsibbledata.tidyverts.org/,              │
│ https://github.com/tidyverts/tsibbledata/.                               │
│ https://tsibbledata.tidyverts.org/reference/vic_elec.html                │
│                                                                          │
│ URL:                                                                     │
│ https://raw.githubusercontent.com/skforecast/skforecast-                 │
│ datasets/main/data/vic_electricity.csv                                   │
│                                                                          │
│ Shape: 52608 rows x 5 columns                                            │
╰──────────────────────────────────────────────────────────────────────────╯

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 52608 entries, 0 to 52607
Data columns (total 5 columns):
 #   Column       Non-Null Count  Dtype  
---  ------       --------------  -----  
 0   Time         52608 non-null  object 
 1   Demand       52608 non-null  float64
 2   Temperature  52608 non-null  float64
 3   Date         52608 non-null  object 
 4   Holiday      52608 non-null  bool   
dtypes: bool(1), float64(2), object(2)
memory usage: 1.7+ MB

The Time column is stored as a string in UTC (note the trailing Z of each value), whereas the original dataset is expressed in the local time of Melbourne. To convert it to datetime, the function pd.to_datetime() is used with utc=True. Once in datetime format, and to make use of pandas functionalities, it is set as an index and converted to the Australia/Melbourne time zone with tz_convert(). Since the data was recorded every 30 minutes, the frequency '30min' is also specified.

# Data preparation
# ==============================================================================
data['Time'] = pd.to_datetime(data['Time'], utc=True)
data = data.set_index('Time')
data = data.tz_convert('Australia/Melbourne')
data = data.sort_index()
data = data.asfreq('30min')
data.head(2)

One of the first analyses to be carried out when working with time series is to check that the series is complete, that is, that there are no missing values.

# Verify that a temporal index is complete
# ==============================================================================
start_date = data.index.min()
end_date = data.index.max()
complete_date_range = pd.date_range(
    start=start_date, end=end_date, freq=data.index.freq
)
is_index_complete = data.index.equals(complete_date_range)
print(f'Index complete: {is_index_complete}')
print(f'Number of rows with missing values: {data.isnull().any(axis=1).sum()}')

Index complete: True
Number of rows with missing values: 0

# Fill gaps in a temporal index
# ==============================================================================
# data.asfreq(freq='30min', fill_value=np.nan)

Although the data is at 30-minute intervals, the aim is to create a model capable of predicting hourly electricity demand, so the data needs to be aggregated. This type of transformation can be done very easily by combining the pandas DatetimeIndex index and its resample() method.

It is very important to use the closed='left' and label='right' arguments correctly to avoid introducing future information into the training, leakage). Suppose that values are available for 10:10, 10:30, 10:45, 11:00, 11:12, and 11:30. To obtain the hourly average, the value assigned to 11:00 must be calculated using the values for 10:10, 10:30, and 10:45; and the value assigned to 12:00 must be calculated using the values for 11:00, 11:12, and 11:30.

The 11:00 average does not include the 11:00 point value because in reality the value is not available at that exact time.

# Aggregating in 1H intervals
# ==============================================================================
# The Date column is eliminated so that it does not generate an error when aggregating.
data = data.drop(columns='Date')
data = (
    data
    .resample(rule='h', closed='left', label='right')
    .agg({
        'Demand': 'mean',
        'Temperature': 'mean',
        'Holiday': 'mean',
    })
)
data

After the aggregation, the dataset starts on 2012-01-01 01:00:00 and ends on 2015-01-01 00:00:00 (each timestamp labels the hour that ends at that time). The last record is discarded so that the series ends on 2014-12-31 23:00:00. In addition, in order to optimize the hyperparameters of the model and evaluate its predictive ability, the data is divided into 3 sets: training, validation and test.

# Split data into train-val-test
# ==============================================================================
data = data.loc[:'2014-12-31 23:00:00', :].copy()
end_train = '2013-12-31 23:59:00'
end_validation = '2014-09-30 23:59:00'
data_train = data.loc[: end_train, :].copy()
data_val   = data.loc[end_train:end_validation, :].copy()
data_test  = data.loc[end_validation:, :].copy()

print(
    f'Train dates      : {data_train.index.min()} --- {data_train.index.max()}  '
    f'(n={len(data_train)})'
)
print(
    f'Validation dates : {data_val.index.min()} --- {data_val.index.max()}  '
    f'(n={len(data_val)})'
)
print(
    f'Test dates       : {data_test.index.min()} --- {data_test.index.max()}  '
    f'(n={len(data_test)})'
)

Train dates      : 2012-01-01 01:00:00+11:00 --- 2013-12-31 23:00:00+11:00  (n=17543)
Validation dates : 2014-01-01 00:00:00+11:00 --- 2014-09-30 23:00:00+10:00  (n=6553)
Test dates       : 2014-10-01 00:00:00+10:00 --- 2014-12-31 23:00:00+11:00  (n=2207)

Graphic exploration¶

Graphical exploration of time series can be an effective way of identifying trends, patterns, and seasonal variations. This, in turn, helps to guide the selection of the most appropriate forecasting model.

Plot time series¶

Full time series

# Interactive plot of time series
# ==============================================================================
fig = go.Figure()
for partition, name in zip(
    [data_train, data_val, data_test], ['Train', 'Validation', 'Test']
):
    fig.add_trace(
        go.Scatter(x=partition.index, y=partition['Demand'], mode='lines', name=name)
    )
fig.update_layout(
    title='Hourly energy demand',
    xaxis_title='Time',
    yaxis_title='Demand',
    legend_title='Partition:',
    width=800,
    height=400,
    margin=dict(l=20, r=20, t=35, b=20),
    legend=dict(orientation='h', yanchor='top', y=1, xanchor='left', x=0.001)
)
# fig.update_xaxes(rangeslider_visible=True)
fig.show()

The graph above shows that electricity demand has an annual seasonality. There is a peak in July and very pronounced peaks in demand between January and March. Since Victoria is in the southern hemisphere, the July peak corresponds to the winter (heating), while the peaks between January and March are caused by summer heat waves (air conditioning).

Section of the time series

Due to the variance of the time series, the intraday pattern cannot be appreciated in a chart of the full series.

# Zooming time series chart
# ==============================================================================
zoom = ('2013-05-01 14:00:00','2013-06-01 14:00:00')
fig, axs = plt.subplots(2, 1, figsize=(8, 4), gridspec_kw={'height_ratios': [1, 2]})
data['Demand'].plot(ax=axs[0], color='black', alpha=0.5)
axs[0].axvspan(zoom[0], zoom[1], color='blue', alpha=0.7)
axs[0].set_title('Electricity demand')
axs[0].set_xlabel('')
data.loc[zoom[0] : zoom[1], 'Demand'].plot(ax=axs[1], color='blue')
axs[1].set_title(f'Zoom: {zoom[0]} to {zoom[1]}', fontsize=10)
plt.tight_layout()
plt.show()

When the time series is zoomed in, a clear weekly seasonality can be seen, with higher consumption during the working week (Monday to Friday) and lower consumption at weekends. There is also a clear correlation between the consumption of one day and that of the previous day.

Seasonality plots¶

Seasonal plots are a useful tool for identifying seasonal patterns and trends in a time series. They are created by averaging the values of each season over time and then plotting them against time.

# Annual, weekly and daily seasonality
# ==============================================================================
fig, axs = plt.subplots(2, 2, figsize=(8, 5), sharex=False, sharey=True)
axs = axs.ravel()
flierprops = {'markersize': 3, 'alpha': 0.3}

# Demand distribution by month
data['month'] = data.index.month
data.boxplot(column='Demand', by='month', ax=axs[0], flierprops=flierprops)
data.groupby('month')['Demand'].median().plot(style='o-', linewidth=0.8, ax=axs[0])
axs[0].set_ylabel('Demand')
axs[0].set_title('Demand distribution by month', fontsize=9)

# Demand distribution by week day (1 = Monday)
data['week_day'] = data.index.day_of_week + 1
data.boxplot(column='Demand', by='week_day', ax=axs[1], flierprops=flierprops)
data.groupby('week_day')['Demand'].median().plot(style='o-', linewidth=0.8, ax=axs[1])
axs[1].set_ylabel('Demand')
axs[1].set_title('Demand distribution by week day', fontsize=9)

# Demand distribution by the hour of the day (0 to 23, local time)
data['hour_day'] = data.index.hour
data.boxplot(column='Demand', by='hour_day', ax=axs[2], flierprops=flierprops)
# Boxes are drawn at positions 1 to 24, so the medians are plotted at the same positions
median_hour = data.groupby('hour_day')['Demand'].median()
axs[2].plot(range(1, 25), median_hour.to_numpy(), 'o-', linewidth=0.8)
axs[2].set_ylabel('Demand')
axs[2].set_title('Demand distribution by the hour of the day', fontsize=9)

# Demand distribution by week day and hour of the day
mean_day_hour = data.groupby(['week_day', 'hour_day'])['Demand'].mean()
mean_day_hour.plot(ax=axs[3])
axs[3].set(
    title       = 'Mean Demand during week',
    xticks      = [i * 24 for i in range(7)],
    xticklabels = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun'],
    xlabel      = 'Day and hour',
    ylabel      = 'Mean Demand'
)
axs[3].title.set_size(10)

fig.suptitle('Seasonality plots', fontsize=12)
fig.tight_layout()

Based on the plots, the electrical grid exhibits a highly predictable, cyclical pattern typical of a region in the Southern Hemisphere with distinct seasonal and residential behaviors.

Annual and Seasonal Behavior

• Winter Heating Dominates Baseline Demand: The months of June, July, and August (months 6 to 8) show the highest median energy consumption. This indicates a consistent, heavy reliance on heating throughout the Australian winter.

• Summer Cooling Creates Extreme Peaks: January and February (months 1 and 2) exhibit lower median demand but feature massive upward outliers. This highlights that while baseline summer consumption is lower, extreme heatwaves trigger intense, simultaneous air conditioning use across the grid.

• Shoulder Seasons are Stable: Spring (September to November) and autumn (March to May) demonstrate the lowest overall demand and the tightest data distribution, representing periods where neither severe heating nor cooling is required.

Weekly Activity Patterns

• Strong Commercial Influence: Days 1 through 5 (Monday to Friday) maintain high and consistent energy usage, reflecting standard industrial and commercial operational hours.

• Weekend Load Reduction: Days 6 and 7 (Saturday and Sunday) show a significant drop in baseline demand. The absence of commercial activity drives this reduction, though high-demand outliers still occasionally occur.

Daily Intra-Day Cycles

• Overnight Trough: The lowest energy consumption reliably occurs between 03:00 and 05:00 when the population is asleep and commercial activity is paused.

• The Evening Peak: The most critical daily stress on the grid happens between 18:00 and 20:00. This represents the moment people return home from work, turn on climate control, cook, and use domestic appliances.

• The Morning Ramp-Up: A secondary, smaller spike occurs around 08:00 to 09:00 as businesses open and households wake up, which is clearly visible in the continuous weekly mean line plot.

Autocorrelation plots¶

Autocorrelation plots are a useful tool for identifying the order of an autoregressive model. The autocorrelation function (ACF) is a measure of the correlation between the time series and a lagged version of itself. The partial autocorrelation function (PACF) is a measure of the correlation between the time series and a lagged version of itself, controlling for the values of the time series at all shorter lags. These plots are useful for identifying the lags to be included in the autoregressive model.

# Autocorrelation plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(5, 2))
plot_acf(data['Demand'], ax=ax, lags=60, fft=True)
plt.show()

# Partial autocorrelation plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(5, 2))
plot_pacf(data['Demand'], ax=ax, lags=60, method='burg')
plt.show()

# Top 10 lags with the highest absolute partial autocorrelation
# ==============================================================================
calculate_lag_autocorrelation(
    data    = data['Demand'],
    n_lags  = 60,
    sort_by = 'partial_autocorrelation_abs'
).head(10)

The autocorrelation plot demonstrates a strong correlation between demand in one hour and prior hours, as well as between demand in one hour and the corresponding hour in preceding days. The partial autocorrelation table shows that the most informative lags are the most recent ones (1 and 2) and those located around one day before (24, 25 and 26). This observed correlation suggests that autoregressive models may be effective in this scenario.

Baseline¶

When faced with a forecasting problem, it is important to establish a baseline model. This is usually a very simple model that can be used as a reference to assess whether more complex models are worth implementing.

Skforecast allows you to easily create a baseline with its class ForecasterEquivalentDate (see the baseline forecaster user guide). This model, also known as Seasonal Naive Forecasting, simply returns the value observed in the same period of the previous season (e.g., the same working day from the previous week, the same hour from the previous day, etc.).

Based on the exploratory analysis performed, the baseline model will be the one that predicts each hour using the value of the same hour on the previous day.

# Create baseline: value of the same hour of the previous day
# ==============================================================================
# The offset is expressed as a number of steps (24 hours). With a time zone aware
# index, a calendar offset such as pd.DateOffset(days=1) fails on daylight saving
# time transitions because some local times do not exist.
forecaster = ForecasterEquivalentDate(
                 offset    = 24,
                 n_offsets = 1
             )

# Train forecaster
# ==============================================================================
forecaster.fit(y=data.loc[:end_validation, 'Demand'])
forecaster

# Backtesting
# ==============================================================================
cv = TimeSeriesFold(
        steps              = 24,
        initial_train_size = len(data.loc[:end_validation]),
        refit              = False
)
metric, predictions = backtesting_forecaster(
                          forecaster = forecaster,
                          y          = data['Demand'],
                          cv         = cv,
                          metric     = 'mean_absolute_error'
                       )
metric_baseline = metric
metric_baseline

The error of the baseline model is used as a reference to assess whether the more complex models are worth implementing.

Recursive multi-step forecasting¶

A recursive autoregressive model ForecasterRecursive is trained using a gradient boosting estimator, LGBMRegressor, to predict energy demand for the next 24 hours.

The predictors used are the demand values from the past 24 hours (lags 1 to 24) and the moving average of the past 3 days (72 hours), which is created with the RollingFeatures class. The estimator's hyperparameters are left at their default values.

# Create forecaster
# ==============================================================================
# Lags: demand of the last 24 hours
lags = 24
window_features = RollingFeatures(stats=['mean'], window_sizes=24 * 3)
forecaster = ForecasterRecursive(
                 estimator       = LGBMRegressor(random_state=15926, verbose=-1),
                 lags            = lags,
                 window_features = window_features
             )

# Train forecaster
# ==============================================================================
forecaster.fit(y=data.loc[:end_validation, 'Demand'])
forecaster

Backtesting¶

To obtain a robust estimate of the model's predictive ability, a backtesting process is performed. The backtesting process consists of generating a forecast for each observation in the test set, following the same procedure as would be done in production, and then comparing the predicted value to the actual value.

The backtesting process is applied using the backtesting_forecaster() function. For this use case, the simulation is carried out as follows: the model is trained with data from 2012-01-01 01:00 to 2014-09-30 23:00, and then it predicts the next 24 hours every day at 23:59. The error metric used is the Mean Absolute Error (MAE).

It is highly recommended to review the documentation for the backtesting_forecaster() function to gain a better understanding of its capabilities. This will help to utilize its full potential to analyze the predictive ability of the model.

# Backtesting
# ==============================================================================
metric, predictions = backtesting_forecaster(
                          forecaster    = forecaster,
                          y             = data['Demand'],
                          cv            = cv,
                          metric        = 'mean_absolute_error',
                          verbose       = True,  # Set to False to avoid printing
                      )
metric_recursive_no_exog = metric

Information of folds
--------------------
Number of observations used for initial training: 24096
Number of observations used for backtesting: 2207
    Number of folds: 92
    Number skipped folds: 0 
    Number of steps per fold: 24
    Number of steps to exclude between last observed data (last window) and predictions (gap): 0
    Last fold only includes 23 observations.

Fold: 0
    Training:   2012-01-01 01:00:00+11:00 -- 2014-09-30 23:00:00+10:00  (n=24096)
    Validation: 2014-10-01 00:00:00+10:00 -- 2014-10-01 23:00:00+10:00  (n=24)
Fold: 1
    Training:   No training in this fold
    Validation: 2014-10-02 00:00:00+10:00 -- 2014-10-02 23:00:00+10:00  (n=24)
Fold: 2
    Training:   No training in this fold
    Validation: 2014-10-03 00:00:00+10:00 -- 2014-10-03 23:00:00+10:00  (n=24)
Fold: 3
    Training:   No training in this fold
    Validation: 2014-10-04 00:00:00+10:00 -- 2014-10-04 23:00:00+10:00  (n=24)
Fold: 4
    Training:   No training in this fold
    Validation: 2014-10-05 00:00:00+10:00 -- 2014-10-06 00:00:00+11:00  (n=24)
Fold: 5
    Training:   No training in this fold
    Validation: 2014-10-06 01:00:00+11:00 -- 2014-10-07 00:00:00+11:00  (n=24)
Fold: 6
    Training:   No training in this fold
    Validation: 2014-10-07 01:00:00+11:00 -- 2014-10-08 00:00:00+11:00  (n=24)
Fold: 7
    Training:   No training in this fold
    Validation: 2014-10-08 01:00:00+11:00 -- 2014-10-09 00:00:00+11:00  (n=24)
Fold: 8
    Training:   No training in this fold
    Validation: 2014-10-09 01:00:00+11:00 -- 2014-10-10 00:00:00+11:00  (n=24)
Fold: 9
    Training:   No training in this fold
    Validation: 2014-10-10 01:00:00+11:00 -- 2014-10-11 00:00:00+11:00  (n=24)
Fold: 10
    Training:   No training in this fold
    Validation: 2014-10-11 01:00:00+11:00 -- 2014-10-12 00:00:00+11:00  (n=24)
Fold: 11
    Training:   No training in this fold
    Validation: 2014-10-12 01:00:00+11:00 -- 2014-10-13 00:00:00+11:00  (n=24)
Fold: 12
    Training:   No training in this fold
    Validation: 2014-10-13 01:00:00+11:00 -- 2014-10-14 00:00:00+11:00  (n=24)
Fold: 13
    Training:   No training in this fold
    Validation: 2014-10-14 01:00:00+11:00 -- 2014-10-15 00:00:00+11:00  (n=24)
Fold: 14
    Training:   No training in this fold
    Validation: 2014-10-15 01:00:00+11:00 -- 2014-10-16 00:00:00+11:00  (n=24)
Fold: 15
    Training:   No training in this fold
    Validation: 2014-10-16 01:00:00+11:00 -- 2014-10-17 00:00:00+11:00  (n=24)
Fold: 16
    Training:   No training in this fold
    Validation: 2014-10-17 01:00:00+11:00 -- 2014-10-18 00:00:00+11:00  (n=24)
Fold: 17
    Training:   No training in this fold
    Validation: 2014-10-18 01:00:00+11:00 -- 2014-10-19 00:00:00+11:00  (n=24)
Fold: 18
    Training:   No training in this fold
    Validation: 2014-10-19 01:00:00+11:00 -- 2014-10-20 00:00:00+11:00  (n=24)
Fold: 19
    Training:   No training in this fold
    Validation: 2014-10-20 01:00:00+11:00 -- 2014-10-21 00:00:00+11:00  (n=24)
Fold: 20
    Training:   No training in this fold
    Validation: 2014-10-21 01:00:00+11:00 -- 2014-10-22 00:00:00+11:00  (n=24)
Fold: 21
    Training:   No training in this fold
    Validation: 2014-10-22 01:00:00+11:00 -- 2014-10-23 00:00:00+11:00  (n=24)
Fold: 22
    Training:   No training in this fold
    Validation: 2014-10-23 01:00:00+11:00 -- 2014-10-24 00:00:00+11:00  (n=24)
Fold: 23
    Training:   No training in this fold
    Validation: 2014-10-24 01:00:00+11:00 -- 2014-10-25 00:00:00+11:00  (n=24)
Fold: 24
    Training:   No training in this fold
    Validation: 2014-10-25 01:00:00+11:00 -- 2014-10-26 00:00:00+11:00  (n=24)
Fold: 25
    Training:   No training in this fold
    Validation: 2014-10-26 01:00:00+11:00 -- 2014-10-27 00:00:00+11:00  (n=24)
Fold: 26
    Training:   No training in this fold
    Validation: 2014-10-27 01:00:00+11:00 -- 2014-10-28 00:00:00+11:00  (n=24)
Fold: 27
    Training:   No training in this fold
    Validation: 2014-10-28 01:00:00+11:00 -- 2014-10-29 00:00:00+11:00  (n=24)
Fold: 28
    Training:   No training in this fold
    Validation: 2014-10-29 01:00:00+11:00 -- 2014-10-30 00:00:00+11:00  (n=24)
Fold: 29
    Training:   No training in this fold
    Validation: 2014-10-30 01:00:00+11:00 -- 2014-10-31 00:00:00+11:00  (n=24)
Fold: 30
    Training:   No training in this fold
    Validation: 2014-10-31 01:00:00+11:00 -- 2014-11-01 00:00:00+11:00  (n=24)
Fold: 31
    Training:   No training in this fold
    Validation: 2014-11-01 01:00:00+11:00 -- 2014-11-02 00:00:00+11:00  (n=24)
Fold: 32
    Training:   No training in this fold
    Validation: 2014-11-02 01:00:00+11:00 -- 2014-11-03 00:00:00+11:00  (n=24)
Fold: 33
    Training:   No training in this fold
    Validation: 2014-11-03 01:00:00+11:00 -- 2014-11-04 00:00:00+11:00  (n=24)
Fold: 34
    Training:   No training in this fold
    Validation: 2014-11-04 01:00:00+11:00 -- 2014-11-05 00:00:00+11:00  (n=24)
Fold: 35
    Training:   No training in this fold
    Validation: 2014-11-05 01:00:00+11:00 -- 2014-11-06 00:00:00+11:00  (n=24)
Fold: 36
    Training:   No training in this fold
    Validation: 2014-11-06 01:00:00+11:00 -- 2014-11-07 00:00:00+11:00  (n=24)
Fold: 37
    Training:   No training in this fold
    Validation: 2014-11-07 01:00:00+11:00 -- 2014-11-08 00:00:00+11:00  (n=24)
Fold: 38
    Training:   No training in this fold
    Validation: 2014-11-08 01:00:00+11:00 -- 2014-11-09 00:00:00+11:00  (n=24)
Fold: 39
    Training:   No training in this fold
    Validation: 2014-11-09 01:00:00+11:00 -- 2014-11-10 00:00:00+11:00  (n=24)
Fold: 40
    Training:   No training in this fold
    Validation: 2014-11-10 01:00:00+11:00 -- 2014-11-11 00:00:00+11:00  (n=24)
Fold: 41
    Training:   No training in this fold
    Validation: 2014-11-11 01:00:00+11:00 -- 2014-11-12 00:00:00+11:00  (n=24)
Fold: 42
    Training:   No training in this fold
    Validation: 2014-11-12 01:00:00+11:00 -- 2014-11-13 00:00:00+11:00  (n=24)
Fold: 43
    Training:   No training in this fold
    Validation: 2014-11-13 01:00:00+11:00 -- 2014-11-14 00:00:00+11:00  (n=24)
Fold: 44
    Training:   No training in this fold
    Validation: 2014-11-14 01:00:00+11:00 -- 2014-11-15 00:00:00+11:00  (n=24)
Fold: 45
    Training:   No training in this fold
    Validation: 2014-11-15 01:00:00+11:00 -- 2014-11-16 00:00:00+11:00  (n=24)
Fold: 46
    Training:   No training in this fold
    Validation: 2014-11-16 01:00:00+11:00 -- 2014-11-17 00:00:00+11:00  (n=24)
Fold: 47
    Training:   No training in this fold
    Validation: 2014-11-17 01:00:00+11:00 -- 2014-11-18 00:00:00+11:00  (n=24)
Fold: 48
    Training:   No training in this fold
    Validation: 2014-11-18 01:00:00+11:00 -- 2014-11-19 00:00:00+11:00  (n=24)
Fold: 49
    Training:   No training in this fold
    Validation: 2014-11-19 01:00:00+11:00 -- 2014-11-20 00:00:00+11:00  (n=24)
Fold: 50
    Training:   No training in this fold
    Validation: 2014-11-20 01:00:00+11:00 -- 2014-11-21 00:00:00+11:00  (n=24)
Fold: 51
    Training:   No training in this fold
    Validation: 2014-11-21 01:00:00+11:00 -- 2014-11-22 00:00:00+11:00  (n=24)
Fold: 52
    Training:   No training in this fold
    Validation: 2014-11-22 01:00:00+11:00 -- 2014-11-23 00:00:00+11:00  (n=24)
Fold: 53
    Training:   No training in this fold
    Validation: 2014-11-23 01:00:00+11:00 -- 2014-11-24 00:00:00+11:00  (n=24)
Fold: 54
    Training:   No training in this fold
    Validation: 2014-11-24 01:00:00+11:00 -- 2014-11-25 00:00:00+11:00  (n=24)
Fold: 55
    Training:   No training in this fold
    Validation: 2014-11-25 01:00:00+11:00 -- 2014-11-26 00:00:00+11:00  (n=24)
Fold: 56
    Training:   No training in this fold
    Validation: 2014-11-26 01:00:00+11:00 -- 2014-11-27 00:00:00+11:00  (n=24)
Fold: 57
    Training:   No training in this fold
    Validation: 2014-11-27 01:00:00+11:00 -- 2014-11-28 00:00:00+11:00  (n=24)
Fold: 58
    Training:   No training in this fold
    Validation: 2014-11-28 01:00:00+11:00 -- 2014-11-29 00:00:00+11:00  (n=24)
Fold: 59
    Training:   No training in this fold
    Validation: 2014-11-29 01:00:00+11:00 -- 2014-11-30 00:00:00+11:00  (n=24)
Fold: 60
    Training:   No training in this fold
    Validation: 2014-11-30 01:00:00+11:00 -- 2014-12-01 00:00:00+11:00  (n=24)
Fold: 61
    Training:   No training in this fold
    Validation: 2014-12-01 01:00:00+11:00 -- 2014-12-02 00:00:00+11:00  (n=24)
Fold: 62
    Training:   No training in this fold
    Validation: 2014-12-02 01:00:00+11:00 -- 2014-12-03 00:00:00+11:00  (n=24)
Fold: 63
    Training:   No training in this fold
    Validation: 2014-12-03 01:00:00+11:00 -- 2014-12-04 00:00:00+11:00  (n=24)
Fold: 64
    Training:   No training in this fold
    Validation: 2014-12-04 01:00:00+11:00 -- 2014-12-05 00:00:00+11:00  (n=24)
Fold: 65
    Training:   No training in this fold
    Validation: 2014-12-05 01:00:00+11:00 -- 2014-12-06 00:00:00+11:00  (n=24)
Fold: 66
    Training:   No training in this fold
    Validation: 2014-12-06 01:00:00+11:00 -- 2014-12-07 00:00:00+11:00  (n=24)
Fold: 67
    Training:   No training in this fold
    Validation: 2014-12-07 01:00:00+11:00 -- 2014-12-08 00:00:00+11:00  (n=24)
Fold: 68
    Training:   No training in this fold
    Validation: 2014-12-08 01:00:00+11:00 -- 2014-12-09 00:00:00+11:00  (n=24)
Fold: 69
    Training:   No training in this fold
    Validation: 2014-12-09 01:00:00+11:00 -- 2014-12-10 00:00:00+11:00  (n=24)
Fold: 70
    Training:   No training in this fold
    Validation: 2014-12-10 01:00:00+11:00 -- 2014-12-11 00:00:00+11:00  (n=24)
Fold: 71
    Training:   No training in this fold
    Validation: 2014-12-11 01:00:00+11:00 -- 2014-12-12 00:00:00+11:00  (n=24)
Fold: 72
    Training:   No training in this fold
    Validation: 2014-12-12 01:00:00+11:00 -- 2014-12-13 00:00:00+11:00  (n=24)
Fold: 73
    Training:   No training in this fold
    Validation: 2014-12-13 01:00:00+11:00 -- 2014-12-14 00:00:00+11:00  (n=24)
Fold: 74
    Training:   No training in this fold
    Validation: 2014-12-14 01:00:00+11:00 -- 2014-12-15 00:00:00+11:00  (n=24)
Fold: 75
    Training:   No training in this fold
    Validation: 2014-12-15 01:00:00+11:00 -- 2014-12-16 00:00:00+11:00  (n=24)
Fold: 76
    Training:   No training in this fold
    Validation: 2014-12-16 01:00:00+11:00 -- 2014-12-17 00:00:00+11:00  (n=24)
Fold: 77
    Training:   No training in this fold
    Validation: 2014-12-17 01:00:00+11:00 -- 2014-12-18 00:00:00+11:00  (n=24)
Fold: 78
    Training:   No training in this fold
    Validation: 2014-12-18 01:00:00+11:00 -- 2014-12-19 00:00:00+11:00  (n=24)
Fold: 79
    Training:   No training in this fold
    Validation: 2014-12-19 01:00:00+11:00 -- 2014-12-20 00:00:00+11:00  (n=24)
Fold: 80
    Training:   No training in this fold
    Validation: 2014-12-20 01:00:00+11:00 -- 2014-12-21 00:00:00+11:00  (n=24)
Fold: 81
    Training:   No training in this fold
    Validation: 2014-12-21 01:00:00+11:00 -- 2014-12-22 00:00:00+11:00  (n=24)
Fold: 82
    Training:   No training in this fold
    Validation: 2014-12-22 01:00:00+11:00 -- 2014-12-23 00:00:00+11:00  (n=24)
Fold: 83
    Training:   No training in this fold
    Validation: 2014-12-23 01:00:00+11:00 -- 2014-12-24 00:00:00+11:00  (n=24)
Fold: 84
    Training:   No training in this fold
    Validation: 2014-12-24 01:00:00+11:00 -- 2014-12-25 00:00:00+11:00  (n=24)
Fold: 85
    Training:   No training in this fold
    Validation: 2014-12-25 01:00:00+11:00 -- 2014-12-26 00:00:00+11:00  (n=24)
Fold: 86
    Training:   No training in this fold
    Validation: 2014-12-26 01:00:00+11:00 -- 2014-12-27 00:00:00+11:00  (n=24)
Fold: 87
    Training:   No training in this fold
    Validation: 2014-12-27 01:00:00+11:00 -- 2014-12-28 00:00:00+11:00  (n=24)
Fold: 88
    Training:   No training in this fold
    Validation: 2014-12-28 01:00:00+11:00 -- 2014-12-29 00:00:00+11:00  (n=24)
Fold: 89
    Training:   No training in this fold
    Validation: 2014-12-29 01:00:00+11:00 -- 2014-12-30 00:00:00+11:00  (n=24)
Fold: 90
    Training:   No training in this fold
    Validation: 2014-12-30 01:00:00+11:00 -- 2014-12-31 00:00:00+11:00  (n=24)
Fold: 91
    Training:   No training in this fold
    Validation: 2014-12-31 01:00:00+11:00 -- 2014-12-31 23:00:00+11:00  (n=23)

# Plot predictions vs real value
# ======================================================================================
fig = go.Figure()
fig.add_trace(
    go.Scatter(x=data_test.index, y=data_test['Demand'], name='test', mode='lines')
)
fig.add_trace(
    go.Scatter(
        x=predictions.index, y=predictions['pred'], name='prediction', mode='lines'
    )
)
fig.update_layout(
    title='Real value vs predicted in test data',
    xaxis_title='Date time',
    yaxis_title='Demand',
    width=800,
    height=400,
    margin=dict(l=20, r=20, t=35, b=20),
    legend=dict(orientation='h', yanchor='top', y=1.01, xanchor='left', x=0)
)
fig.show()

# Backtesting error
# ==============================================================================
metric_recursive_no_exog

The autoregressive model achieves a lower MAE than the baseline model, although the improvement is moderate. Using only the past values of the series, the model has no information about the day of the week, whether a day is a holiday, or the temperature, all of which have a strong influence on electricity demand. This motivates the next step: including exogenous variables.

Exogenous variables¶

So far, only lagged values of the time series have been used as predictors. However, it is possible to include other variables as predictors. These variables are known as exogenous variables (features) and their use can improve the predictive capacity of the model. A very important point to keep in mind is that the values of the exogenous variables must be known at the time of prediction.

Common examples of exogenous variables are those derived from the calendar, such as the day of the week, month, year, or holidays. Weather variables such as temperature, humidity, and wind also fall into this category, as do economic variables such as inflation and interest rates.

Next, exogenous variables are created based on calendar information, sunrise and sunset times, temperature, and holidays. These new variables are then added to the training, validation and test sets, and used as predictors in the autoregressive model.

# Calendar features
# ==============================================================================
calendar_transformer = CalendarFeatures(
    features = ['month', 'week', 'day_of_week', 'hour'],
    encoding = 'cyclical',
    keep_original_columns = False,
)
calendar_features = calendar_transformer.fit_transform(data)
calendar_features.head(2)

# Sunlight features
# ==============================================================================
location = LocationInfo(
    latitude  = -37.8,
    longitude = 144.95,
    timezone  = 'Australia/Melbourne'
)
# Sunrise and sunset only depend on the date, so they are calculated once per day
dates = pd.Series(data.index.date, index=data.index)
sun_by_date = {
    date: sun(location.observer, date=date, tzinfo=location.timezone)
    for date in dates.unique()
}
sunrise_hour = dates.map(lambda date: sun_by_date[date]['sunrise'])
sunset_hour = dates.map(lambda date: sun_by_date[date]['sunset'])
sunrise_hour = sunrise_hour.dt.round('h').dt.hour
sunset_hour = sunset_hour.dt.round('h').dt.hour
sunrise_hour_sin = np.sin(2 * np.pi * sunrise_hour / 24)
sunrise_hour_cos = np.cos(2 * np.pi * sunrise_hour / 24)
sunset_hour_sin = np.sin(2 * np.pi * sunset_hour / 24)
sunset_hour_cos = np.cos(2 * np.pi * sunset_hour / 24)

daylight_hours = sunset_hour - sunrise_hour
# Both the index and the sunrise and sunset hours are in Melbourne local time
is_daylight = np.where(
    (data.index.hour >= sunrise_hour) & (data.index.hour < sunset_hour), 1, 0,
)

sun_light_features = pd.DataFrame({
                        'sunrise_hour_sin': sunrise_hour_sin,
                        'sunrise_hour_cos': sunrise_hour_cos,
                        'sunset_hour_sin': sunset_hour_sin,
                        'sunset_hour_cos': sunset_hour_cos,
                        'daylight_hours': daylight_hours,
                        'is_daylight': is_daylight
                     })
sun_light_features.head(2)

# Holiday features
# ==============================================================================
# Public holidays are known in advance, so using the value of the next day as a
# predictor is not data leakage. The shift is expressed in steps (24 hours), so it is
# off by one hour on the two days per year with a daylight saving time transition.
holiday_features = data[['Holiday']].astype(int)
holiday_features['holiday_previous_day'] = holiday_features['Holiday'].shift(24)
holiday_features['holiday_next_day'] = holiday_features['Holiday'].shift(-24)
holiday_features.head(2)

# Rolling windows of temperature
# ==============================================================================
wf_transformer = WindowFeatures(
    variables   = ['Temperature'],
    window      = ['1D', '7D'],
    functions   = ['mean', 'max', 'min'],
    freq        = 'h',
)
temp_features = wf_transformer.fit_transform(data[['Temperature']])
temp_features.head(2)

# Merge all exogenous variables
# ==============================================================================
assert all(calendar_features.index == sun_light_features.index)
assert all(calendar_features.index == temp_features.index)
assert all(calendar_features.index == holiday_features.index)
exogenous_features = pd.concat([
                         calendar_features,
                         sun_light_features,
                         temp_features,
                         holiday_features
                     ], axis=1)

# Due to the creation of moving averages, there are missing values at the beginning
# of the series. And due to holiday_next_day there are missing values at the end.
exogenous_features = exogenous_features.iloc[7 * 24:, :]
exogenous_features = exogenous_features.iloc[:-24, :]
exogenous_features.head(3)

In many cases, exogenous variables are not isolated. Rather, their effect on the target variable depends on the value of other variables. For example, the effect of the hour of the day on electricity demand depends on the day of the week: the morning ramp is much more pronounced on working days than on weekends. The interaction between the exogenous variables can be captured by new variables that are obtained by multiplying existing variables together. These interactions are easily obtained with the PolynomialFeatures class from scikit-learn.

Interactions are created for all pairs of exogenous variables but, to limit the number of predictors, only the interactions between cyclical features (calendar and sunlight) are included in the model in the next step.

# Interaction between exogenous variables
# ==============================================================================
transformer_poly = PolynomialFeatures(
                        degree           = 2,
                        interaction_only = True,
                        include_bias     = False
                    ).set_output(transform='pandas')
poly_cols = [
    'month_sin',
    'month_cos',
    'week_sin',
    'week_cos',
    'day_of_week_sin',
    'day_of_week_cos',
    'hour_sin',
    'hour_cos',
    'sunrise_hour_sin',
    'sunrise_hour_cos',
    'sunset_hour_sin',
    'sunset_hour_cos',
    'daylight_hours',
    'is_daylight',
    'holiday_previous_day',
    'holiday_next_day',
    'Temperature_window_1D_mean',
    'Temperature_window_1D_min',
    'Temperature_window_1D_max',
    'Temperature_window_7D_mean',
    'Temperature_window_7D_min',
    'Temperature_window_7D_max',
    'Temperature',
    'Holiday'
]
poly_features = transformer_poly.fit_transform(exogenous_features[poly_cols])
poly_features = poly_features.drop(columns=poly_cols)
poly_features.columns = [f'poly_{col}' for col in poly_features.columns]
poly_features.columns = poly_features.columns.str.replace(' ', '__')
assert all(poly_features.index == exogenous_features.index)
exogenous_features = pd.concat([exogenous_features, poly_features], axis=1)
exogenous_features.head(3)

# Select exogenous variables to be included in the model
# ==============================================================================
exog_features = []
# Columns that end with _sin or _cos are selected (cyclical features and their
# interactions)
exog_features.extend(
    exogenous_features.filter(regex='_sin$|_cos$').columns.tolist()
)
# Columns that start with Temperature_ are selected
exog_features.extend(
    exogenous_features.filter(regex='^Temperature_.*').columns.tolist()
)
# Columns that start with holiday_ are selected
exog_features.extend(
    exogenous_features.filter(regex='^holiday_.*').columns.tolist()
)
# Include original features
exog_features.extend(['Temperature', 'Holiday', 'daylight_hours', 'is_daylight'])

# Merge target and exogenous variables in the same DataFrame
# ==============================================================================
data = data[['Demand']].merge(
           exogenous_features[exog_features],
           left_index  = True,
           right_index = True,
           how         = 'inner'  # Use only dates for which we have all the variables
       )
data = data.astype('float32')

# Split data into train-val-test
data_train = data.loc[: end_train, :].copy()
data_val   = data.loc[end_train:end_validation, :].copy()
data_test  = data.loc[end_validation:, :].copy()

The model is backtested again, but this time, the exogenous variables are also included as predictors. Since the last 24 hours of the series were removed when creating holiday_next_day, the test set is one day shorter than the one used for the previous models, so the comparison with them is not strictly like for like.

# Backtesting model
# ==============================================================================
# The folds are created again because the length of `data` has changed
cv = TimeSeriesFold(
        steps              = 24,
        initial_train_size = len(data.loc[:end_validation]),
        refit              = False
)

metric, predictions = backtesting_forecaster(
                          forecaster = forecaster,
                          y          = data['Demand'],
                          exog       = data[exog_features],
                          cv         = cv,
                          metric     = 'mean_absolute_error'
                      )
metric_recursive_exog = metric
display(metric_recursive_exog)
predictions.head()

The inclusion of exogenous variables as predictors improves the predictive capacity of the model considerably: the MAE is reduced to approximately half of that obtained with the autoregressive predictors alone.

Hyperparameter tuning¶

The trained ForecasterRecursive object used the first 24 lags and a LGBMRegressor model with the default hyperparameters. However, there is no reason why these values are the most appropriate. For example, the exploratory analysis showed a clear weekly seasonality that the first 24 lags cannot capture, so the candidate sets of lags include, in addition to the last one or two days, the values observed one week before around the same hour (lags 167, 168 and 169). To find the best hyperparameters, a Bayesian Search is performed using the bayesian_search_forecaster function. The search is carried out using the same backtesting process as before, but each time, the model is trained with different combinations of hyperparameters and lags. It is important to note that the hyperparameter search must be done using the validation set, so the test data is never used.

# Hyperparameters search
# ==============================================================================
forecaster = ForecasterRecursive(
                 estimator       = LGBMRegressor(random_state=15926, verbose=-1),
                 lags            = 24,  # This value will be replaced in the search
                 window_features = window_features
             )

# Lags used as predictors
lags_grid = [
    # Previous day
    24,
    # Two previous days
    48,
    # Previous day and same hour (+-1) of the previous week
    list(range(1, 25)) + [167, 168, 169],
    # Most recent hours and same hour (+-1) of the two previous days
    [1, 2, 3, 23, 24, 25, 47, 48, 49],
    # Same as before plus the same hour (+-1) of the previous week
    [1, 2, 3, 23, 24, 25, 47, 48, 49, 167, 168, 169],
]

# Estimator hyperparameters search space
def search_space(trial):
    params = {
        'n_estimators' : trial.suggest_int('n_estimators', 300, 1000, step=100),
        'max_depth'    : trial.suggest_int('max_depth', 3, 10),
        'learning_rate': trial.suggest_float('learning_rate', 0.01, 0.5),
        'reg_alpha'    : trial.suggest_float('reg_alpha', 0, 1),
        'reg_lambda'   : trial.suggest_float('reg_lambda', 0, 1),
        'lags'         : trial.suggest_categorical('lags', lags_grid)
    }
    return params

# Folds training and validation
cv_search = TimeSeriesFold(
                steps              = 24,
                initial_train_size = len(data.loc[:end_train]),
                refit              = False,
            )

results_search, frozen_trial = bayesian_search_forecaster(
    forecaster   = forecaster,
    y            = data.loc[:end_validation, 'Demand'],
    exog         = data.loc[:end_validation, exog_features],
    cv           = cv_search,
    metric       = 'mean_absolute_error',
    search_space = search_space,
    n_trials     = 30,  # Increase for more exhaustive search
    return_best  = True
)

# Search results
# ==============================================================================
best_params = results_search.at[0, 'params']
best_params = best_params | {'random_state': 15926, 'verbose': -1}
best_lags = results_search.at[0, 'lags']
results_search.head(3)

Since return_best has been set to True, the forecaster object is automatically updated with the best configuration found and re-trained on all the data passed to the search (training and validation sets). The test set remains unseen. This final model can then be used for future predictions on new data.

# Best model
# ==============================================================================
forecaster

Once the best combination of hyperparameters has been identified using the validation data, the predictive capacity of the model is evaluated when applied to the test set.

# Backtest final model on test data
# ==============================================================================
metric, predictions = backtesting_forecaster(
                          forecaster = forecaster,
                          y          = data['Demand'],
                          exog       = data[exog_features],
                          cv         = cv,
                          metric     = 'mean_absolute_error'
                      )
metric_recursive_exog_tuned = metric
display(metric_recursive_exog_tuned)
predictions.head()

After optimization of lags and hyperparameters, the prediction error in the test set is reduced further, by around 10%. The best configuration found includes the lags of the previous week, which is consistent with the weekly seasonality identified in the exploratory analysis.

Feature selection¶

Feature selection is the process of selecting a subset of relevant features for use in model construction. It is an important step in the machine learning process, as it can help to reduce overfitting, improve model accuracy, and reduce training time. Since the underlying estimators of skforecast follow the scikit-learn API, it is possible to apply the feature selection methods available in scikit-learn with the function select_features. Two of the most popular methods are Recursive Feature Elimination and Sequential Feature Selection.

# Create forecaster
# ==============================================================================
estimator = LGBMRegressor(
                n_estimators = 100,
                max_depth    = 4,
                random_state = 15926,
                verbose      = -1
            )

forecaster = ForecasterRecursive(
                 estimator       = estimator,
                 lags            = best_lags,
                 window_features = window_features
             )

# Recursive feature elimination with cross-validation
# ==============================================================================
warnings.filterwarnings('ignore', message='X does not have valid feature names.*')
selector = RFECV(
    estimator = estimator,
    step      = 1,
    cv        = 3,
)
lags_select, window_features_select, exog_select, _ = select_features(
    forecaster      = forecaster,
    selector        = selector,
    y               = data_train['Demand'],
    exog            = data_train[exog_features],
    select_only     = None,
    force_inclusion = None,
    subsample       = 0.5,  # Subsample to speed up the process
    random_state    = 123,
    verbose         = True,
)

Recursive feature elimination (RFECV)
-------------------------------------
Total number of records available: 17206
Total number of records used for feature selection: 8603
Number of features available: 118
    Lags            (n=27)
    Window features (n=1)
    Exog            (n=90)
    Calendar        (n=0)
Number of features selected: 33
    Lags            (n=15) : [1, 2, 3, 4, 5, 8, 10, 11, 17, 21, 23, 24, 167, 168, 169]
    Window features (n=1) : ['roll_mean_72']
    Exog            (n=17) : ['day_of_week_sin', 'hour_sin', 'hour_cos', 'poly_week_sin__hour_cos', 'poly_week_cos__hour_sin', 'poly_week_cos__hour_cos', 'poly_day_of_week_sin__hour_sin', 'poly_day_of_week_cos__hour_sin', 'poly_hour_sin__hour_cos', 'poly_hour_sin__sunset_hour_sin', 'poly_hour_sin__sunset_hour_cos', 'poly_hour_cos__sunrise_hour_sin', 'poly_hour_cos__sunset_hour_sin', 'poly_hour_cos__sunset_hour_cos', 'Temperature_window_1D_mean', 'Temperature', 'Holiday']
    Calendar        (n=0) : []

# Keep only the selected window features
# ==============================================================================
# `select_features` returns the names of the selected window features. The
# RollingFeatures object is created again with only the selected statistics. If none
# is selected, None is returned (forecaster without window features).
def filter_rolling_features(window_features, selected_names):
    keep = [
        i for i, name in enumerate(window_features.features_names)
        if name in selected_names
    ]
    if not keep:
        return None

    return RollingFeatures(
        stats          = [window_features.stats[i] for i in keep],
        window_sizes   = [window_features.window_sizes[i] for i in keep],
        min_periods    = [window_features.min_periods[i] for i in keep],
        features_names = [window_features.features_names[i] for i in keep],
        fillna         = window_features.fillna,
        kwargs_stats   = window_features.kwargs_stats,
    )

window_features_select = filter_rolling_features(
    window_features, window_features_select
)
print(f'Selected window features: {window_features_select}')

Selected window features: RollingFeatures(
    stats           = ['mean'],
    window_sizes    = [72],
    Max window size = 72,
    min_periods     = [72],
    features_names  = ['roll_mean_72'],
    fillna          = None
    kwargs_stats    = {'ewm': {'alpha': 0.3}},
)

Scikit-learn's RFECV starts by training a model on the initial set of features, and obtaining the importance of each feature (through attributes such as coef_ or feature_importances_). Then, in each round, the least important features are iteratively removed, followed by cross-validation to calculate the performance of the model with the remaining features. This process continues until further feature removal doesn't improve or starts to degrade the performance of the model (based on a chosen metric), or the min_features_to_select is reached.

The final result is an optimal subset of features that ideally balances model simplicity and predictive power, as determined by the cross-validation process.

Note that the selection is carried out using only the training set. In this way, neither the validation nor the test data influence which predictors are chosen, which would be a form of data leakage.

The forecaster is trained and re-evaluated using the best subset of features. The selected lags and exogenous variables can be passed directly to the forecaster, whereas the RollingFeatures object has to be created again with only the selected statistics.

The fourth output of select_features (ignored in this example) contains the selected calendar features when they are created by the forecaster itself through its calendar_features argument. In this document, calendar features are included as exogenous variables, so the selected ones are already part of exog_select.

# Create a forecaster with the selected features
# ==============================================================================
forecaster = ForecasterRecursive(
                estimator       = LGBMRegressor(**best_params),
                lags            = lags_select,
                window_features = window_features_select
             )
# Backtesting model with exogenous variables on test data
# ==============================================================================
metric, predictions = backtesting_forecaster(
                            forecaster = forecaster,
                            y          = data['Demand'],
                            exog       = data[exog_select],
                            cv         = cv,
                            metric     = 'mean_absolute_error'
                      )
metric_recursive_exog_selection = metric
display(metric_recursive_exog_selection)
predictions.head()

The number of predictors has been reduced to less than a third of those originally available without compromising the performance of the model: the MAE in the test set is very similar to the one obtained with all the predictors. This simplifies the model and speeds up training. It also reduces the risk of overfitting because the model is less likely to learn irrelevant feature noise.

It should be noted that RFECV evaluates the predictors according to their ability to predict the next value of the series (one-step-ahead), using a simple model and a subsample of the data, whereas the forecaster is used to predict 24 steps recursively. For this reason, the result of a feature selection should always be validated with the same backtesting process used to evaluate the model, as done here.

Probabilistic forecasting: Prediction intervals¶

A prediction interval defines the interval within which the true value of the target variable can be expected to be found with a given probability. Skforecast implements several methods for probabilistic forecasting:

• Probabilistic forecasting: Bootstrapping

• Probabilistic forecasting: Conformal prediction

• Probabilistic forecasting: Quantile regression

The following code shows how to generate prediction intervals for the autoregressive model. First, the predict_interval() method is used to generate the prediction intervals for each predicted step. Then, the backtesting_forecaster() function is used to generate the prediction intervals for the entire test set. The interval argument is used to specify the desired coverage probability of the prediction intervals. In this case, interval is set to [0.05, 0.95], which means that the intervals are delimited by the quantiles 0.05 and 0.95, resulting in a theoretical coverage probability of 90%. The intervals are estimated with conformal prediction (method='conformal').

# Create and train forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
                 estimator       = LGBMRegressor(**best_params),
                 lags            = lags_select,
                 window_features = window_features_select,
                 binner_kwargs   = {'n_bins': 5}
             )
forecaster.fit(
    y    = data.loc[:end_train, 'Demand'],
    exog = data.loc[:end_train, exog_select],
    store_in_sample_residuals = True
)

# Predict intervals
# ==============================================================================
# Since the model has been trained with exogenous variables, they must be provided
# for the prediction.
predictions = forecaster.predict_interval(
                  exog     = data.loc[end_train:, exog_select],
                  steps    = 24,
                  interval = [0.05, 0.95],
                  method   = 'conformal',
              )
predictions.head()

By default, intervals are calculated using in-sample residuals (residuals from the training set). However, this can result in intervals that are too narrow (overly optimistic). To avoid this, the set_out_sample_residuals() method is used to store out-sample residuals computed with a validation set through backtesting. This is why the forecaster has been trained using only the training set: the validation data has not been seen by the model, so its residuals are a realistic estimate of the error expected on new data.

If the predicted values are passed to set_out_sample_residuals() in addition to the true values, the residuals are binned according to the magnitude of the prediction they are associated with. Then, the width of the interval can be conditioned on the range of values of the predictions (a different correction factor is calculated for each bin). This can help to improve the coverage of the estimated intervals while keeping them as narrow as possible.

# Backtesting on validation data to obtain out-sample residuals
# ==============================================================================
cv = TimeSeriesFold(
        steps              = 24,
        initial_train_size = len(data.loc[:end_train]),
        refit              = False,
)
metric_val, predictions_val = backtesting_forecaster(
                                  forecaster = forecaster,
                                  y          = data.loc[:end_validation, 'Demand'],
                                  exog       = data.loc[:end_validation, exog_select],
                                  cv         = cv,
                                  metric     = 'mean_absolute_error'
                              )
metric_val

# Out-sample residuals distribution
# ==============================================================================
residuals = data.loc[predictions_val.index, 'Demand'] - predictions_val['pred']
print(pd.Series(np.where(residuals < 0, 'negative', 'positive')).value_counts())
_ = plot_residuals(residuals=residuals, figsize=(7, 4))

negative    3845
positive    2708
Name: count, dtype: int64

The out-sample residuals are not perfectly balanced: there are clearly more negative than positive residuals, which means that the model tends to overestimate the demand in the validation period more often than it underestimates it. Since conformal intervals are symmetric around the prediction, a bias in the residuals can make the empirical coverage deviate from the nominal coverage.

# Store out-sample residuals in the forecaster
# ==============================================================================
forecaster.set_out_sample_residuals(
    y_true = data.loc[predictions_val.index, 'Demand'],
    y_pred = predictions_val['pred']
)

The backtesting process is then run to estimate the prediction intervals in the test set. The argument use_in_sample_residuals is set to False so that the previously stored out-sample residuals are used, and use_binned_residuals is set to True so that the width of the intervals is conditioned on the range of the predicted values.

# Backtesting with prediction intervals in test data using out-sample residuals
# ==============================================================================
cv = TimeSeriesFold(
        steps              = 24,
        initial_train_size = len(data.loc[:end_validation]),
        refit              = False,
)
metric, predictions = backtesting_forecaster(
    forecaster              = forecaster,
    y                       = data['Demand'],
    exog                    = data[exog_select],
    cv                      = cv,
    metric                  = 'mean_absolute_error',
    interval                = [0.05, 0.95],
    interval_method         = 'conformal',
    use_in_sample_residuals = False,  # Use out-sample residuals
    use_binned_residuals    = True,   # Intervals conditioned on the predicted values
)
predictions.head(5)

# Plot prediction intervals vs real value
# ==============================================================================
fig = go.Figure([
    go.Scatter(
        name='Prediction', x=predictions.index, y=predictions['pred'], mode='lines',
    ),
    go.Scatter(
        name='Real value', x=data_test.index, y=data_test['Demand'], mode='lines',
    ),
    go.Scatter(
        name='Upper Bound', x=predictions.index, y=predictions['upper_bound'],
        mode='lines', marker=dict(color='#444'), line=dict(width=0), showlegend=False
    ),
    go.Scatter(
        name='Lower Bound', x=predictions.index, y=predictions['lower_bound'],
        marker=dict(color='#444'), line=dict(width=0), mode='lines',
        fillcolor='rgba(68, 68, 68, 0.3)', fill='tonexty', showlegend=False
    )
])
fig.update_layout(
    title='Real value vs predicted in test data',
    xaxis_title='Date time',
    yaxis_title='Demand',
    width=800,
    height=400,
    margin=dict(l=20, r=20, t=35, b=20),
    hovermode='x',
    legend=dict(orientation='h', yanchor='top', y=1.1, xanchor='left', x=0.001)
)
fig.show()

# Predicted interval coverage (on test data)
# ==============================================================================
coverage = calculate_coverage(
              y_true       = data.loc[predictions.index, 'Demand'],
              lower_bound  = predictions['lower_bound'],
              upper_bound  = predictions['upper_bound']
           )
area = (predictions['upper_bound'] - predictions['lower_bound']).sum()
print(f'Total area of the interval: {round(area, 2)}')
print(f'Predicted interval coverage: {round(100 * coverage, 2)} %')

Total area of the interval: 1196003.7
Predicted interval coverage: 91.39 %

The observed coverage of the intervals is close to the theoretically expected coverage (90%). Conformal prediction only achieves the nominal coverage if the residuals used for calibration are representative of the errors the model will make in the future, so it is good practice to monitor the empirical coverage over time.

Model explainability and interpretability¶

Due to the complex nature of many modern machine learning models, such as ensemble methods, they often function as black boxes, making it difficult to understand why a particular prediction was made. Explainability techniques aim to demystify these models, providing insight into their inner workings and helping to build trust, improve transparency, and meet regulatory requirements in various domains. Enhancing model explainability not only helps to understand model behavior, but also helps to identify biases, improve model performance, and enable stakeholders to make more informed decisions based on machine learning insights.

Skforecast is compatible with some of the most popular model explainability methods: model-specific feature importances, SHAP values, and partial dependence plots.

# Create and train forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
                 estimator       = LGBMRegressor(**best_params),
                 lags            = lags_select,
                 window_features = window_features_select
             )
forecaster.fit(
    y    = data.loc[:end_validation, 'Demand'],
    exog = data.loc[:end_validation, exog_select]
)

Model-specific feature importance¶

# Model-specific feature importances
# ==============================================================================
feature_importances = forecaster.get_feature_importances()
feature_importances.head(10)

SHAP values¶

SHAP (SHapley Additive exPlanations) values are a popular method for explaining machine learning models, as they help to understand how variables and values influence predictions visually and quantitatively.

It is possible to generate SHAP-values explanations from skforecast models with just two essential elements:

• The internal estimator of the forecaster.

• The training matrices created from the time series and exogenous features, used to fit the forecaster. They can be obtained with the create_train_X_y() method.

By leveraging these two components, users can create insightful and interpretable explanations for their skforecast models. These explanations can be used to verify the reliability of the model, identify the most significant factors that contribute to model predictions, and gain a deeper understanding of the underlying relationship between the input variables and the target variable.

# Training matrices used by the forecaster to fit the internal estimator
# ==============================================================================
X_train, y_train = forecaster.create_train_X_y(
                       y    = data.loc[:end_validation, 'Demand'],
                       exog = data.loc[:end_validation, exog_select]
                   )
display(X_train.head(3))
display(y_train.head(3))

Time
2012-01-15 02:00:00+11:00    3713.539551
2012-01-15 03:00:00+11:00    3755.494873
2012-01-15 04:00:00+11:00    3466.537598
Freq: h, Name: y, dtype: float32

# Create SHAP explainer
# ==============================================================================
shap.initjs()
explainer = shap.TreeExplainer(forecaster.estimator)

# Sample 50% of the data to speed up the calculation
X_train_sample = X_train.sample(frac=0.5, random_state=785412)
shap_values = explainer.shap_values(X_train_sample)

# Shap summary plot (top 10)
# ==============================================================================
shap.summary_plot(shap_values, X_train_sample, max_display=10, show=False)
fig, ax = plt.gcf(), plt.gca()
ax.set_title('SHAP Summary plot')
ax.tick_params(labelsize=8)
fig.set_size_inches(6, 4.5)

SHAP values not only allow for interpreting the general behavior of the model but also serve as a powerful tool for analyzing individual predictions. This is especially useful when trying to understand how a specific prediction was made and which variables contributed to it.

To carry out this analysis, it is necessary to access the predictor values (lags, window features and exogenous variables used by the model) at the time of the prediction. This can be achieved by using the create_predict_X() method or by enabling the return_predictors=True argument in the backtesting_forecaster() function.

Suppose one wants to understand the prediction obtained during the backtesting for the date 2014-12-16 12:00:00.

# Backtesting returning the predictors
# ==============================================================================
cv = TimeSeriesFold(
        steps              = 24,
        initial_train_size = len(data.loc[:end_validation]),
        refit              = False,
)
_, predictions = backtesting_forecaster(
                        forecaster        = forecaster,
                        y                 = data['Demand'],
                        exog              = data[exog_select],
                        cv                = cv,
                        metric            = 'mean_absolute_error',
                        return_predictors = True,
                )

By setting return_predictors=True, a DataFrame is obtained with the predicted value ('pred'), the partition it belongs to ('fold'), and the value of the lags and exogenous variables used to make each prediction.

# Predictions and predictors
# ==============================================================================
predictions.head(3)

# Waterfall for a single prediction generated during backtesting
# ==============================================================================
predictors = predictions.drop(columns=['fold', 'pred'])
# Ensure that the types are the same as in the training matrices
predictors = predictors.astype(data[exog_select].dtypes)
iloc_predicted_date = predictions.index.get_loc('2014-12-16 12:00:00')
shap_values_single = explainer(predictors)
shap.plots.waterfall(shap_values_single[iloc_predicted_date], show=False)
fig = plt.gcf()
fig.set_size_inches(8, 3.5)
fig.axes[0].tick_params(labelsize=8)
plt.show()

# Forceplot for a single prediction generated during backtesting
# ==============================================================================
shap.force_plot(
    base_value  = shap_values_single.base_values[iloc_predicted_date],
    shap_values = shap_values_single.values[iloc_predicted_date],
    features    = predictors.iloc[iloc_predicted_date, :],
)

Direct multi-step forecasting¶

The ForecasterRecursive model follows a recursive strategy in which each new prediction is based on the previous one. Another strategy for multi-step forecasting involves training a separate model for each step to be predicted. This is known as direct multi-step forecasting, implemented in the ForecasterDirect class. Although more computationally expensive than the recursive approach due to the need to train multiple models, it may yield better results.

# Forecaster with direct method
# ==============================================================================
forecaster = ForecasterDirect(
                 estimator       = LGBMRegressor(**best_params),
                 steps           = 24,
                 lags            = lags_select,
                 window_features = window_features_select
             )

# Backtesting model
# ==============================================================================
metric, predictions = backtesting_forecaster(
                          forecaster = forecaster,
                          y          = data['Demand'],
                          exog       = data[exog_select],
                          cv         = cv,
                          metric     = 'mean_absolute_error'
                      )
metric_direct_exog_selection = metric
display(metric_direct_exog_selection)
predictions.head()

The direct multi-step forecasting model outperforms the recursive model trained with the same predictors, reducing the mean absolute error by around 10%. Since each step has its own model, the direct strategy is less affected by the accumulation of errors along the forecast horizon. However, it is important to keep in mind its higher computational cost when assessing whether it is worth implementing.

Anticipated daily forecast¶

So far, we have evaluated the model under the assumption that the forecasts for the next day are generated at exactly 11:59 PM each day. However, this approach is impractical because there is insufficient time to plan and manage operations for the early hours of the next day.

Now, suppose that the predictions for the next day need to be made at 11:00 AM each day to allow enough time. This means that at 11:00 on day $D$ you have to forecast the hours [12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23] of the same day and the hours [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23] of day $D+1$. This means that a total of 36 hours into the future have to be predicted, although only the last 24 hours have to be stored.

This type of evaluation can be easily done by combining the backtesting_forecaster() function with the gap argument of TimeSeriesFold. In addition, the allow_incomplete_fold argument of TimeSeriesFold controls whether the last fold is kept when it does not have the required number of steps (in this example, its default value, True, is used). The process adapted to this scenario is run on a daily basis and consists of the following steps:

1. At 11:00 a.m. on the first day of the test set, the next 36 hours (the remaining 12 hours of the day plus 24 hours of the following day) are predicted.

2. Only the forecasts for the next day are stored, i.e. starting from position 12.

3. The next day until 11:00 a.m. is added to the test set.

4. The process is repeated.

Thus, at 11:00 a.m. each day, the model has access to the actual demand values recorded up to that time.

# End of initial_train_size + 12 positions
# ==============================================================================
data.iloc[:len(data.loc[:end_validation]) + 12].tail(2)

# Forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
                 estimator       = LGBMRegressor(**best_params),
                 lags            = lags_select,
                 window_features = window_features_select
             )

# Backtesting with gap
# ==============================================================================
cv = TimeSeriesFold(
        steps              = 24,
        initial_train_size = len(data.loc[:end_validation]) + 12,
        refit              = False,
        gap                = 12,
)

metric, predictions = backtesting_forecaster(
                          forecaster = forecaster,
                          y          = data['Demand'],
                          exog       = data[exog_select],
                          cv         = cv,
                          metric     = 'mean_absolute_error'
                      )
display(metric)
predictions.head(5)

As expected, the error increases as the forecast horizon increases from 24 to 36 hours.

Conclusions¶

The use of gradient boosting models has proven to be a powerful tool for forecasting energy demand. One of the main advantages of these models is that they can easily incorporate exogenous variables, which can significantly improve the predictive power of the model. In addition, the use of explainability techniques can help to visually and quantitatively understand how variables and values affect predictions. All of these issues are easily addressed using the skforecast library.

The evolution of the mean absolute error (MAE) in the test set, shown in the table below, summarizes the contribution of each step:

• A recursive forecaster using only the last 24 lags and a rolling mean improves the baseline model (same hour of the previous day), but only moderately.

• Adding exogenous variables (calendar, sunlight, temperature and holidays) is the step with the largest impact: the error is reduced to approximately half.

• Tuning lags and hyperparameters provides an additional reduction of around 10%. The best configuration includes the lags of the previous week.

• Feature selection keeps less than a third of the predictors with a very similar error, which results in a simpler and faster model.

• With the same predictors, the direct strategy achieves the lowest error, at a higher computational cost.

• When the forecast must be issued 12 hours in advance, the error increases, as expected for a longer forecast horizon.

# Results
# ======================================================================================
forecaster_type = [
    'ForecasterEquivalentDate (Baseline)', 'ForecasterRecursive',
    'ForecasterRecursive', 'ForecasterRecursive', 'ForecasterRecursive',
    'ForecasterDirect'
]
exog_included = [
    'False', 'False', 'True', 'True', 'True (Feature Selection)',
    'True (Feature Selection)'
]
tuned = ['False', 'False', 'False', 'True', 'True', 'True']
metrics = pd.concat(
    [
        metric_baseline, metric_recursive_no_exog, metric_recursive_exog,
        metric_recursive_exog_tuned, metric_recursive_exog_selection,
        metric_direct_exog_selection
    ],
    axis=0,
)
metrics.insert(0, 'Forecaster', forecaster_type)
metrics.insert(1, 'Exogenous Variables', exog_included)
metrics.insert(2, 'Tuned Hyperparameters', tuned)
metrics = (
    metrics.reset_index(drop=True).round(2).sort_values(by='mean_absolute_error')
)
metrics

Session information¶

import session_info
session_info.show(html=False)

-----
astral              3.2
feature_engine      1.9.4
lightgbm            4.7.0
matplotlib          3.10.9
numpy               2.4.6
optuna              4.9.0
pandas              2.3.3
plotly              6.9.0
session_info        v1.0.1
shap                0.52.0
skforecast          0.25.0
sklearn             1.7.2
statsmodels         0.14.6
-----
IPython             9.15.0
jupyter_client      8.9.1
jupyter_core        5.9.1
-----
Python 3.13.14 | packaged by conda-forge | (main, Jun 12 2026, 09:44:26) [MSC v.1944 64 bit (AMD64)]
Windows-11-10.0.26200-SP0
-----
Session information updated at 2026-09-22 09:26

Citation¶

How to cite this document

If you use this document or any part of it, please acknowledge the source, thank you!

Forecasting energy demand with machine learning by Joaquín Amat Rodrigo and Javier Escobar Ortiz, available under Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0 DEED) at https://www.cienciadedatos.net/documentos/py29-forecasting-electricity-power-demand-python.html

How to cite skforecast

If you use skforecast for a publication, we would appreciate it if you cite the published software.

Zenodo:

Amat Rodrigo, Joaquin, & Escobar Ortiz, Javier. (2026). skforecast (v0.25.0). Zenodo. https://doi.org/10.5281/zenodo.8382788

APA:

Amat Rodrigo, J., & Escobar Ortiz, J. (2026). skforecast (Version 0.25.0) [Computer software]. https://doi.org/10.5281/zenodo.8382788

BibTeX:

@software{skforecast, author = {Amat Rodrigo, Joaquin and Escobar Ortiz, Javier}, title = {skforecast}, version = {0.25.0}, month = {09}, year = {2026}, license = {BSD-3-Clause}, url = {https://skforecast.org/}, doi = {10.5281/zenodo.8382788} }

Did you like the article? Your support is important

Your contribution will help me to continue generating free educational content. Many thanks! 😊

This work by Joaquín Amat Rodrigo and Javier Escobar Ortiz is licensed under a Attribution-NonCommercial-ShareAlike 4.0 International.

Allowed:

• Share: copy and redistribute the material in any medium or format.

• Adapt: remix, transform, and build upon the material.

Under the following terms:

• Attribution: You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.

• NonCommercial: You may not use the material for commercial purposes.

• ShareAlike: If you remix, transform, or build upon the material, you must distribute your contributions under the same license as the original.