More about forecasting in cienciadedatos.net
- ARIMA and SARIMAX models with python
- Time series forecasting with machine learning
- Forecasting time series with gradient boosting: XGBoost, LightGBM and CatBoost
- Forecasting time series with XGBoost
- Global Forecasting Models: Multi-series forecasting
- Global Forecasting Models: Comparative Analysis of Single and Multi-Series Forecasting Modeling
- Probabilistic forecasting
- Forecasting with deep learning
- Forecasting energy demand with machine learning
- Forecasting web traffic with machine learning
- Intermittent demand forecasting
- Modelling time series trend with tree-based models
- Bitcoin price prediction with Python
- Stacking ensemble of machine learning models to improve forecasting
- Interpretable forecasting models
- Mitigating the Impact of Covid on Forecasting Models
- Forecasting time series with missing values

Introduction¶
The M5 Accuracy competition dataset involves the unit sales of 3,049 products, classified in 3 product categories (Hobbies, Foods, and Household), and 7 product departments in which the above-mentioned categories are disaggregated. The products are sold across 10 stores, located in 3 States (CA, TX, and WI). The competition’s objective was to produce the most accurate point forecasts for 42,840 time series that represent the hierarchical unit sales of the largest retail company in the world, Walmart.
The following are some of the main characteristics of the M5 Accuracy competition dataset:
M5 consisted of grouped, highly correlated series, organized in a hierarchical, cross-sectional structure, thus representing the forecasting set-up of a typical retail company.
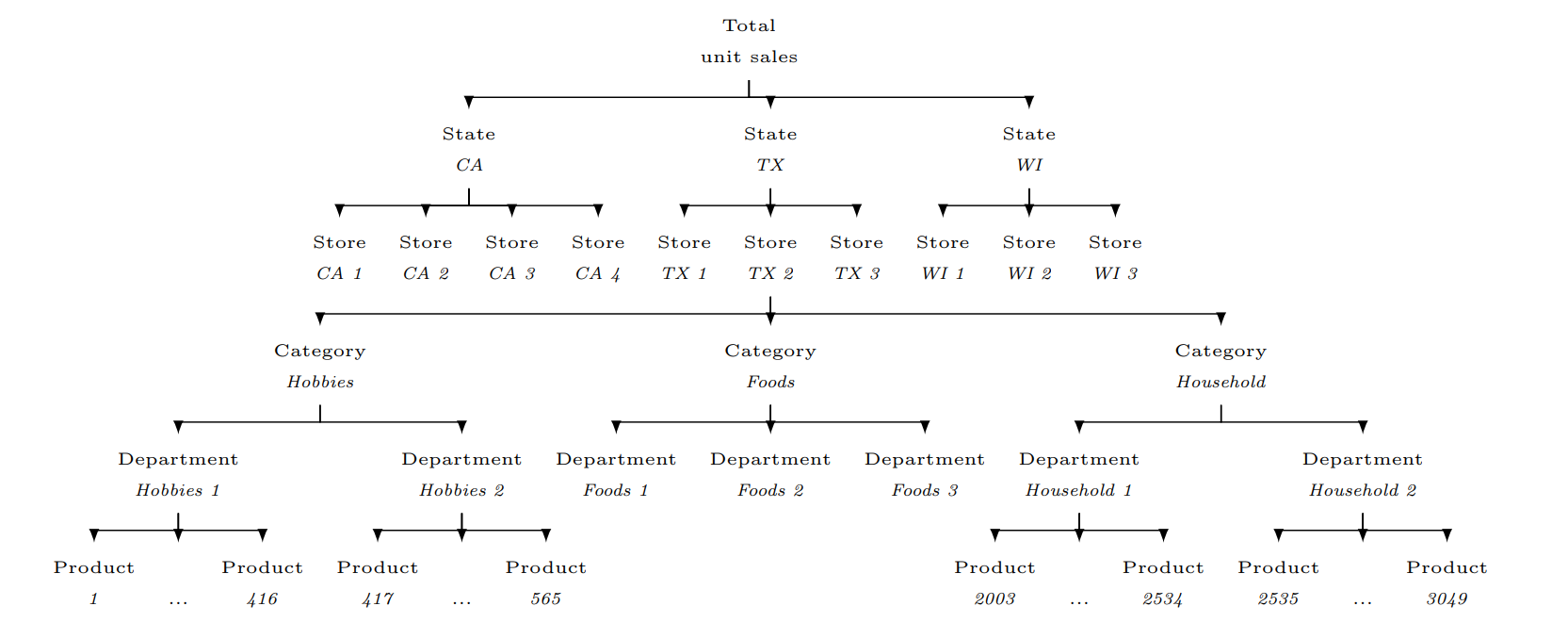
Time series hierarchy
The competition involved series that display intermittency, i.e., sporadic demand including many zeros.
The data is daily and covers the period from 2011-01-29 to 2016-06-19 (1,969 days or approximately 5.4 years). The first 1,913 days of data (2011-01-29 to 2016-04-24) were initially provided to the participating teams as a train set, days 1,914 to 1941 (2016-04-25 to 2016-05-22) served as a validation set, while the remaining 28 days, i.e., 1,942 to 1,969 (2016-05-23 to 2016-06-19), were used as a test set.
Special events and holidays (e.g. Super Bowl, Valentine’s Day, and Orthodox Easter) are organized into four classes: Sporting, Cultural, National, and Religious.
Selling prices are provided on a week-store level (average across seven days). If not available, this means that the product was not available during the week examined. Although prices are constant on a weekly basis, they may change with time. Note: The absence of a selling price means the product was not available for sale. However, there may be instances where a selling price is recorded (indicating availability) even if no sales occurred during that period.
SNAP 8 activities that serve as promotions. This is a binary variable (0 or 1) indicating whether the stores of CA, TX or WI allow SNAP purchases on the date examined. 1 indicates that SNAP purchases are allowed. The United States federal government provides a nutrition assistance benefit called the Supplement Nutrition Assistance Program (SNAP). SNAP provides low income families and individuals with an Electronic Benefits Transfer debit card to purchase food products. In many states, the monetary benefits are dispersed to people across 10 days of the month and on each of these days 1/10 of the people will receive the benefit on their card.
M5 Accuracy competition utilized a variant of the MASE originally proposed by Hyndman & Koehler (2006), to be called Root Mean Squared Scaled Error (RMSSE). The measure is defined as follows:
$$ \text{RMSSE} = \sqrt{ \frac{\frac{1}{h} \sum_{t=n+1}^{n+h} (y_t - \hat{y}_t)^2}{\frac{1}{n-1} \sum_{t=2}^{n} (y_t - y_{t-1})^2}} $$
where $(y_t)$ is the actual value of the series at time $(t)$, $(\hat{y}_t)$ is the forecasted value of the series at time $(t)$, $(n)$ is the length of the training set, and $(h)$ is the forecast horizon. Note that the denominator of RMSSE (in-sample, one-step-ahead mean squared error of the Naive method) is computed only for the periods during which the examined product(s) are actively sold, i.e., the periods following the first non-zero demand observed for the series under evaluation. This is done since many of the products included in the dataset started being sold later than the first available date. Like MASE, RMSSE is independent of the scale of the data, has a predictable behavior, i.e., becomes infinite or undefined only when all the errors of the Naive method are equal to zero, has a defined mean and a finite variance, and is symmetric in the sense that it penalizes positive and negative forecast errors, as well as errors in large and small forecasts, equally.
After estimating RMSSE for all the 42,840 time series of the competition (average accuracy reported for each series across the complete forecasting horizon), the overall accuracy of the forecasting method is computed by averaging the RMSSE scores across all the series of the dataset using appropriate weights. The measure, to be called Weighted RMSSE (WRMSSE), is defined as follows:
$$ \text{WRMSSE} = \sum_{i=1}^{42,840} \frac{w_i \times \text{RMSSE}_i}{\sum_{i=1}^{42,840} w_i} $$
where $(w_i)$ is the weight of the $(i)$-th series. The weights are computed based on the last 28 observations of the training sample of the dataset, specifically based on the cumulative actual dollar sales that each series displayed in that particular period (sum of units sold multiplied by their respective price). Lower WRMSSE scores indicate more accurate forecasts. In other words, we expect the “best” performing forecasting methods to derive lower forecasting errors for the series that are more valuable to the company.
The performance of the top 25 teams of the M5 Accuracy competition in terms of WRMSSE. The results are presented both per aggregation level and overall. Overall percentage improvements are also reported in comparison to the top-performing benchmark (ES bu)
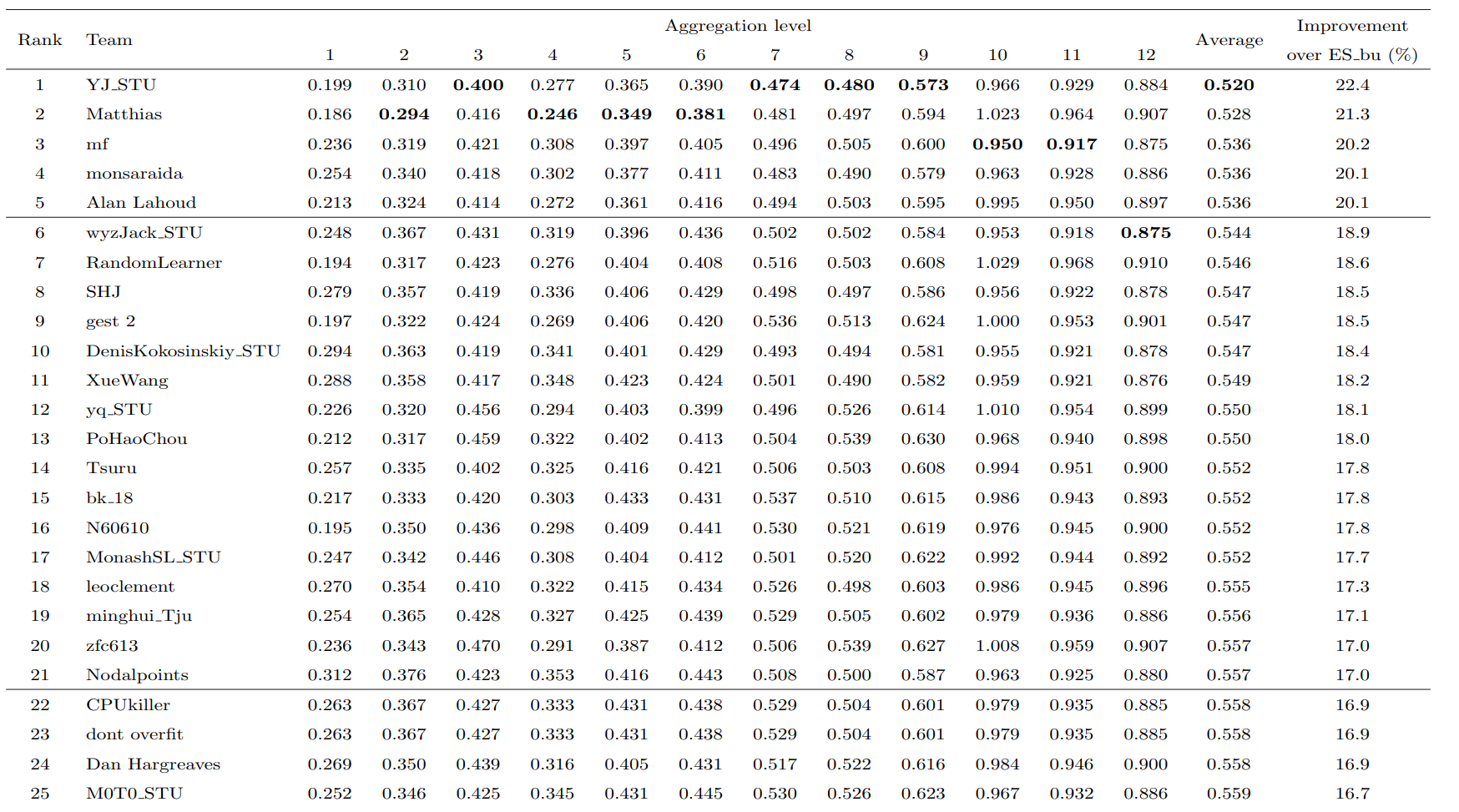
The performance of the top 25 teams
The winner of the competition, considered an equal weighted combination (arithmetic mean) of various LightGBM models that were trained to produce forecasts for the product-store series using data per store (10 models), store-category (30 models), and store-department (70 models). Two variations were considered for each type of model, the first applying a recursive and the second a non-recursive forecasting approach (Bontempi et al., 2013). The models were optimized without considering early stopping and by maximizing the negative log-likelihood of the Tweedie distribution (Zhou et al., 2020), which is considered an effective approach when dealing with data with a probability mass of zero and nonnegative, highly right-skewed distribution.
Most of the top-performing teams employed global forecasting approaches with machine learning methods like gradient boosting (e.g., LightGBM), proving the effectiveness of such approach in handling the complexity of modeling thousands of time series.
Sources:
For more details about the M5 Accuracy competition, you can refer to the following sources:
Makridakis, Spyros & Spiliotis, Evangelos & Assimakopoulos, Vassilis. (2020). The M5 Accuracy competition: Results, findings and conclusions. https://statmodeling.stat.columbia.edu/wp-content/uploads/2021/10/M5_accuracy_competition.pdf
WRMSSE and the M5 Dataset https://www.pmorgan.com.au/tutorials/wrmsse-for-the-m5-dataset/
✎ Note
This document serves as an introduction to the M5 dataset and the application of global models for forecasting thousands of time series simultaneously. To achieve metrics comparable to those of the top participants, users will need to delve deeper and apply additional efforts, such as: hyperparameters tuning, feature selection, using an ensemble of models and incorporating additional features.⚠ Warning
Modelling all the series of the M5 dataset simultaneously is computationally expensive, user will require a powerful machine with at least 100GB of RAM. When not having access to such resources, users can consider working with a subset of the data as shown in section Select a subset of the data.Libraries¶
The libraries used in this document are:
# Data processing
# ==============================================================================
import pandas as pd
import numpy as np
from skforecast.datasets import fetch_dataset
# Plots
# ==============================================================================
import matplotlib.pyplot as plt
import plotly.express as px
import plotly.io as pio
import plotly.offline as poff
pio.templates.default = "seaborn"
poff.init_notebook_mode(connected=True)
plt.style.use('seaborn-v0_8-darkgrid')
# Modelling and Forecasting
# ==============================================================================
import sklearn
import skforecast
import lightgbm
from lightgbm import LGBMRegressor
from sklearn.preprocessing import OrdinalEncoder
from sklearn.compose import make_column_transformer
from skforecast.recursive import ForecasterRecursiveMultiSeries
from skforecast.model_selection import TimeSeriesFold
from skforecast.model_selection import backtesting_forecaster_multiseries
from skforecast.preprocessing import RollingFeatures
from skforecast.preprocessing import series_long_to_dict
from skforecast.preprocessing import exog_long_to_dict
from feature_engine.creation import CyclicalFeatures
from m5_wrmsse import wrmsse # To calculate the metric without the need of submitting to Kaggle
# Warnings configuration
# ==============================================================================
import warnings
warnings.filterwarnings('once')
print(f"Skforecast version: {skforecast.__version__}")
print(f"Scikit-learn version: {sklearn.__version__}")
print(f"LightGBM version: {lightgbm.__version__}")
Data¶
# Download data
# ==============================================================================
data = fetch_dataset("m5")
print(f"Data shape: {data.shape}")
data.head(3)
Se unifican las columnas de eventos (event_name_1, event_name_2) en una única columna binaria. Se unifican también las columnas con el tipo de evento (event_type_1, event_type_2) en una única columna.
# Unificar columns
# ==============================================================================
data['is_event'] = (data['event_name_1'].notnull() | data['event_name_2'].notnull()).astype(int)
data['event_type_1_2'] = data['event_type_1'].fillna('') + data['event_type_2'].fillna('')
data['event_type_1_2'] = data['event_type_1_2'].replace('', 'no_event')
data = data.drop(columns=['event_name_1', 'event_type_1', 'event_name_2', 'event_type_2'])
print(f"Data shape: {data.shape}")
data.head(3)
Intermittent sales¶
Some series exhibit intermittent sales, characterized by frequent zero values. This pattern can arise for various reasons. For example, a product might only be sold during specific seasons or exclusively during promotional periods. Forecasting such series can be challenging, making it essential to identify and handle them appropriately.
In this dataset, there are two distinct scenarios where sales are recorded as zero:
Sales are 0, but a selling price is available: This indicates that the product was available for purchase, but no sales occurred.
Sales are 0, and no selling price is available: This implies that the product was not available for purchase during that period.
Skforecast supports modeling time series of varying lengths. To avoid misleading the model, dates when a product was unavailable for purchase are excluded from the historical data. The following preprocessing steps are applied for each product:
Remove leading missing values in the selling price: This eliminates historical dates before the product was introduced to the market.
Remove trailing missing values in the selling price: This excludes historical dates after the product was retired from the market.
Handle intermediate missing values in selling price: For gaps within the data where the product is not available (missing selling price) but the product was previously available, a new variable,
is_available, is added with a value of0to indicate unavailability.
# Remove dates when the product was not available
# ==============================================================================
def clean_no_sales(df):
"""
Remove head and tail rows from a df where column 'sell_price' is NaN.
"""
non_missing_indices = df['sell_price'].notna()
first_non_zero = np.argmax(non_missing_indices)
last_non_zero = len(df) - np.argmax(non_missing_indices[::-1])
trimmed_df = df.iloc[first_non_zero:last_non_zero]
return trimmed_df
data = (
data
.groupby('id', observed=True)
.apply(clean_no_sales, include_groups=False)
.reset_index(drop=False)
.drop(columns='level_1')
)
data['is_available'] = data['sell_price'].notna().astype(float)
print(f"Data shape: {data.shape}")
data.head(3)
# Number of series with high, low and non intermittent sales
# ==============================================================================
pct_zero_sales = data.groupby('id', observed=True)['sales'].apply(lambda x: (x == 0).mean()).mul(100).round(2)
pct_zero_sales = pct_zero_sales.to_frame(name='pct_zero_sales').sort_values('pct_zero_sales', ascending=False)
high_intermittent = pct_zero_sales[pct_zero_sales['pct_zero_sales'] > 80].shape[0]
medium_intermittent = pct_zero_sales[(pct_zero_sales['pct_zero_sales'] >= 50) & (pct_zero_sales['pct_zero_sales'] < 80)].shape[0]
low_intermittent = pct_zero_sales[(pct_zero_sales['pct_zero_sales'] >= 5) & (pct_zero_sales['pct_zero_sales'] < 50)].shape[0]
# All series have at least few zero sales due to the festive days
non_intermittent = pct_zero_sales[pct_zero_sales['pct_zero_sales'] < 5].shape[0]
print(f"High intermittent sales: {high_intermittent}")
print(f"Medium intermittent sales: {medium_intermittent}")
print(f"Low intermittent sales: {low_intermittent}")
print(f"Non intermittent sales (<5% days): {non_intermittent}")
# Example of high, low and non intermittent series
# ==============================================================================
ids = [
"FOODS_1_090_CA_3_evaluation",
"FOODS_3_778_CA_2_evaluation",
"FOODS_3_555_CA_3_evaluation",
]
sample = data.query("id.isin(@ids)")
fig = px.line(sample, x="datetime", y="sales", facet_row="id", color="id")
fig.update_yaxes(matches=None)
fig.for_each_annotation(lambda a: a.update(text=''))
fig.update_layout(
title="Sales of some intermittent series",
xaxis_title="",
yaxis_title="sales",
width=800,
height=450,
margin=dict(l=20, r=20, t=35, b=20),
legend=dict(orientation="h", yanchor="top")
)
fig.show()
Select a subset of the data¶
# Select only the series with low or non intermittent sales
# ==============================================================================
# ids = pct_zero_sales[pct_zero_sales['pct_zero_sales'] < 50].index
# data = data[data['id'].isin(ids)].reset_index(drop=True)
# print(f"Data shape: {data.shape}")
# print(f"Number of selected series: {data['id'].nunique()}")
# data.head(3)
Feature engineering¶
In adition to the provided exogenous variables, new ones are created:
Calendar features: Day of the week, month, year, etc.
Event related features: is next day an event, was last day an event, etc.
Price features: Average price of the product in the last 7, 14, 30, 60, and 180 days.
⚠ Warning
When creating new features in a multi-series dataset, it is important to avoid avoid mixing information of different series. It is recommended to use thegroupby and apply methods to create these features.
# Calendar features
# ==============================================================================
data['month'] = data['datetime'].dt.month
data['quarter'] = data['datetime'].dt.quarter
data['week'] = data['datetime'].dt.isocalendar().week
data['day_of_week'] = data['datetime'].dt.dayofweek
data['day_of_month'] = data['datetime'].dt.day
data['day_of_year'] = data['datetime'].dt.dayofyear
data['weekend'] = data['day_of_week'].isin([5, 6]).astype(int)
print(f"Data shape: {data.shape}")
data.head(3)
# Cyclical encoding of calendar features
# ==============================================================================
features_to_encode = [
"month",
"quarter",
"week",
"day_of_week",
"day_of_month",
"day_of_year",
]
max_values = {
"month": 12,
"quarter": 4,
"week": 54,
"day_of_week": 6,
"day_of_month": 31,
"day_of_year": 365,
}
cyclical_encoder = CyclicalFeatures(
variables = features_to_encode,
max_values = max_values,
drop_original = True
)
data = cyclical_encoder.fit_transform(data)
# Cast padas types Float64 to numpy float64
# ==============================================================================
data['week_sin'] = data['week_sin'].astype(np.float64)
data['week_cos'] = data['week_cos'].astype(np.float64)
print(f"Data shape: {data.shape}")
data.head(3)
# Event features
# ==============================================================================
def create_event_features(df):
"""
Create additional features based on events. Since the frequency of the series
is daily, shift 1 is the previous and shift -1 is the next day.
"""
df['is_event_lag_1'] = df['is_event'].shift(1)
df['is_event_lag_2'] = df['is_event'].shift(2)
df['is_event_next_1'] = df['is_event'].shift(-1)
df['is_event_next_2'] = df['is_event'].shift(-2)
# Drop rows with NaNs introduced by the shift
df = df.iloc[2:-2]
return df
data = (
data
.groupby('id', observed=True)
.apply(create_event_features, include_groups=False)
.reset_index(drop=False)
.drop(columns='level_1')
)
print(f"Data shape: {data.shape}")
data.head(3)
# Price features
# ==============================================================================
def create_price_features(df):
"""
Create additional features based on price. Price is constant at weekly level,
therefore we can use shift 7 to get the previous week.
"""
df['sell_price_lag_7'] = df['sell_price'].shift(7)
df['sell_price_lag_14'] = df['sell_price'].shift(14)
df['sell_price_lag_21'] = df['sell_price'].shift(21)
df['sell_price_mean_21'] = df['sell_price'].rolling(21, min_periods=1).mean()
df['sell_price_delta_21'] = df['sell_price'] - df['sell_price_lag_21']
# Drop rows with NaNs introduced by the shift
df = df.iloc[21:]
return df
data = (
data
.groupby('id', observed=True)
.apply(create_price_features, include_groups=False)
.reset_index(drop=False)
.drop(columns='level_1')
)
print(f"Data shape: {data.shape}")
data.head(3)
Modelling and forecasting¶
ForecasterRecursiveMultiSeries allows modeling time series of different lengths and using different exogenous variables. When series have different lengths, the data must be transformed into a dictionary. The keys of the dictionary are the names of the series and the values are the series themselves. To do this, the series_long_to_dict function is used, which takes the DataFrame in "long format" and returns a dict of pandas Series. Similarly, when the exogenous variables are different (values or variables) for each series, the data must be transformed into a dictionary. The keys of the dictionary are the names of the series and the values are the exogenous variables themselves. The exog_long_to_dict function is used, which takes the DataFrame in "long format" and returns a dict of exogenous variables (pandas Series or pandas DataFrame).
When all series have the same length and the same exogenous variables, it is not necessary to use dictionaries. Series can be passed as unique DataFrame with each series in a column, and exogenous variables can be passed as a DataFrame with the same length as the series.
# Partitions dates: validation and test set is of 28 days each to match the Kaggle competition
# ==============================================================================
max_date = data['datetime'].max()
min_date = data['datetime'].min()
init_train = min_date
end_train = max_date - pd.DateOffset(days=28*2)
end_val = max_date - pd.DateOffset(days=28)
print(f"Training set : {init_train.date()} - {end_train.date()}")
print(f"Validation set : {(end_train + pd.DateOffset(days=1)).date()} - {end_val.date()}")
print(f"Test set : {(end_val + pd.DateOffset(days=1)).date()} - {max_date.date()}")
# Exogenous features selected for modeling
# ==============================================================================
exog_features = [
"dept_id",
"cat_id",
"store_id",
"state_id",
"snap_CA",
"snap_TX",
"snap_WI",
"sell_price",
"is_event",
"event_type_1_2",
"weekend",
"month_sin",
"month_cos",
"quarter_sin",
"quarter_cos",
"week_sin",
"week_cos",
"day_of_week_sin",
"day_of_week_cos",
"day_of_month_sin",
"day_of_month_cos",
"day_of_year_sin",
"day_of_year_cos",
"is_event_lag_1",
"is_event_lag_2",
"is_event_next_1",
"is_event_next_2",
"sell_price_lag_7",
"sell_price_lag_14",
"sell_price_lag_21",
"sell_price_mean_21",
"sell_price_delta_21",
"is_available"
]
# Transform series and exog to dictionaries
# ==============================================================================
series_dict = series_long_to_dict(
data = data.reset_index(),
series_id = 'id',
index = 'datetime',
values = 'sales',
freq = 'D'
)
exog_dict = exog_long_to_dict(
data = data[exog_features + ['id', 'datetime']].reset_index(),
series_id = 'id',
index = 'datetime',
freq = 'D'
)
exog_dict = {k: v[exog_features] for k, v in exog_dict.items()}
# Missing values per series
# ==============================================================================
missing_values = {k: v.isna().sum() for k, v in series_dict.items() if v.isna().sum() > 0}
missing_values
Since only two series have missing values and the number of missing entries is minimal, linear interpolation is used to impute them. Although this step is unnecessary when using skforecast—since it accommodates missing values in both the series and exogenous variables—it is performed to minimize warnings and to enable the use of regressors that do not support missing values.
# Fill missing values of the target series with interpolation
# ==============================================================================
series_with_missing = ['FOODS_3_150_CA_3_evaluation', 'HOUSEHOLD_1_291_WI_1_evaluation']
for series in series_with_missing:
series_dict[series] = series_dict[series].interpolate(method='linear', limit_direction='both')
# Fill missing
# ==============================================================================
for series in series_with_missing:
exog_dict[series][['snap_CA', 'snap_TX', 'snap_WI', 'is_event', 'weekend']] = (
exog_dict[series][['snap_CA', 'snap_TX', 'snap_WI', 'is_event', 'weekend']].fillna(0).astype(int)
)
# Partition data in train and test
# ==============================================================================
data = data.set_index('datetime').sort_index()
series_dict_train = {k: v.loc[v.index <= end_train,] for k, v in series_dict.items()}
series_dict_valid = {k: v.loc[(v.index > end_train) & (v.index <= end_val),] for k, v in series_dict.items()}
series_dict_test = {k: v.loc[v.index > end_val,] for k, v in series_dict.items()}
exog_dict_train = {k: v.loc[v.index <= end_train,] for k, v in exog_dict.items()}
exog_dict_valid = {k: v.loc[(v.index > end_train) & (v.index <= end_val),] for k, v in exog_dict.items()}
exog_dict_test = {k: v.loc[v.index > end_val,] for k, v in exog_dict.items()}
print(
f"Rage of dates available : {data.index.min()} --- {data.index.max()} "
f"(n={(data.index.max() - data.index.min()).days})"
)
print(
f" Dates for training : {data.index[data.index <= end_train,].min()} --- {data.index[data.index <= end_train,].max()} "
f"(n={data.index[data.index <= end_train,].nunique()})"
)
print(
f" Dates for validation : {data.index[(data.index > end_train) & (data.index <= end_val),].min()} --- {data.index[(data.index > end_train) & (data.index <= end_val),].max()} "
f"(n={data.index[(data.index > end_train) & (data.index <= end_val),].nunique()})"
)
print(
f" Dates for test : {data.index[data.index > end_val,].min()} --- {data.index[data.index > end_val,].max()} "
f"(n={data.index[data.index > end_val,].nunique()})"
)
del data
# Encoding for categorical features
# ==============================================================================
# A ColumnTransformer is used to transform categorical (not numerical) features
# using ordinal encoding. Numeric features are left untouched. Missing values
# are coded as -1. If a new category is found in the test set, it is encoded
# as -1.
categorical_features = ['dept_id', 'cat_id', 'store_id', 'state_id', 'event_type_1_2']
transformer_exog = make_column_transformer(
(
OrdinalEncoder(
dtype=float,
handle_unknown="use_encoded_value",
unknown_value=np.nan,
encoded_missing_value=np.nan
),
categorical_features
),
remainder="passthrough",
verbose_feature_names_out=False,
).set_output(transform="pandas")
transformer_exog
# Create forecaster
# ==============================================================================
window_features = RollingFeatures(stats=['mean', 'min', 'max'], window_sizes=7)
forecaster = ForecasterRecursiveMultiSeries(
estimator = LGBMRegressor(random_state=8520, verbose=-1),
lags = 14,
window_features = window_features,
transformer_series = None,
transformer_exog = transformer_exog,
fit_kwargs = {'categorical_feature': categorical_features},
encoding = "ordinal",
dropna_from_series = True,
)
forecaster
# Backtesting on test set
# ==============================================================================
cv = TimeSeriesFold(
initial_train_size = 1885 + 28, # training + validation
steps = 28,
refit = False
)
metrics, predictions = backtesting_forecaster_multiseries(
forecaster = forecaster,
series = series_dict,
exog = exog_dict,
cv = cv,
metric = ['mean_absolute_error', 'root_mean_squared_scaled_error'],
verbose = True,
show_progress = True,
suppress_warnings = True
)
display(predictions.head())
display(metrics)
Metric WRMSSE¶
The python library m5_wrmsse allows to calculate the WRMSSE metric for the M5 dataset whitout the need of submitting the results to Kaggle. It evaluates all 30490 series, so all them must be forecasted.
# Calculate WRMSSE using the library m5_wrmsse
# ==============================================================================
predictions_wide = predictions.transpose()
predictions_wide.columns = [f'F{i+1}' for i in range(28)]
predictions_wide.columns.name = None
predictions_wide.index.name = 'id'
display(predictions_wide.head(3))
# The wrmsse expect a numpy array of shape (30490, 28), this is 28 days of forecast for each of the 30490 series
metric = wrmsse(predictions_wide.to_numpy())
print(f"WRMSSE: {metric}")
Next steps¶
The pressented example is a simple approach to the M5 dataset. To achieve better results, users can consider the following steps:
Use a different loss function: Optimize the models using a different loss function.
Session information¶
import session_info
session_info.show(html=False)
Citation¶
How to cite this document
If you use this document or any part of it, please acknowledge the source, thank you!
The M5 Accuracy competition: the success of global forecasting models by Joaquín Amat Rodrigo and Javier Escobar Ortiz, available under Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0 DEED) at https://cienciadedatos.net/documentos/py61-m5-forecasting-competition.html
How to cite skforecast
If you use skforecast for a publication, we would appreciate it if you cite the published software.
Zenodo:
Amat Rodrigo, Joaquin, & Escobar Ortiz, Javier. (2024). skforecast (v0.14.0). Zenodo. https://doi.org/10.5281/zenodo.8382788
APA:
Amat Rodrigo, J., & Escobar Ortiz, J. (2024). skforecast (Version 0.14.0) [Computer software]. https://doi.org/10.5281/zenodo.8382788
BibTeX:
@software{skforecast, author = {Amat Rodrigo, Joaquin and Escobar Ortiz, Javier}, title = {skforecast}, version = {0.14.0}, month = {11}, year = {2024}, license = {BSD-3-Clause}, url = {https://skforecast.org/}, doi = {10.5281/zenodo.8382788} }
Did you like the article? Your support is important
Your contribution will help me to continue generating free educational content. Many thanks! 😊
This work by Joaquín Amat Rodrigo and Javier Escobar Ortiz is licensed under a Attribution-NonCommercial-ShareAlike 4.0 International.
Allowed:
-
Share: copy and redistribute the material in any medium or format.
-
Adapt: remix, transform, and build upon the material.
Under the following terms:
-
Attribution: You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
-
NonCommercial: You may not use the material for commercial purposes.
-
ShareAlike: If you remix, transform, or build upon the material, you must distribute your contributions under the same license as the original.


