If you like Skforecast , please give us a star on GitHub! ⭐️
Forecasting web traffic with machine learning and Python
More about forecasting
- Skforecast: time series forecasting with Python and Scikit-learn
- Forecasting electricity demand with Python
- Forecasting time series with gradient boosting: Skforecast, XGBoost, LightGBM and CatBoost
- Bitcoin price prediction with Python, when the past does not repeat itself
- Prediction intervals in forecasting models
- Multi-series forecasting
- Reducing the influence of Covid-19 on time series forecasting models
- Forecasting time series with missing values
- Intermittent demand forecasting
Introduction¶
A time series is a succession of chronologically ordered data spaced at equal or unequal intervals. The forecasting process consists of predicting the future value of a time series, either by modeling the series solely based on its past behavior (autoregressive) or by using other external variables. This document describes how to use machine learning and statistical models in order to forecast the number of users who visit a website.
Use case¶
The history of daily visits to the website cienciadedatos.net is available since 07/01/2020. The goal is to generate a forecasting model capable of predicting the web traffic during the next 7 days. The user wants to be able to run the model every Monday and obtain daily traffic predictions for the rest of the week.
To evaluate the performance of the model according to its intended use, it is advisable not to predict only the last 7 days of the time series, but to simulate the whole process. Backtesting is a special type of cross-validation applied to the previous period(s) and can be used with different strategies:
Backtesting with refit and increasing training size (fixed origin)
The model is trained each time before making predictions. With this configuration, the model uses all the data available so far. It is a variation of the standard cross-validation but, instead of making a random distribution of the observations, the training set increases sequentially, maintaining the temporal order of the data.
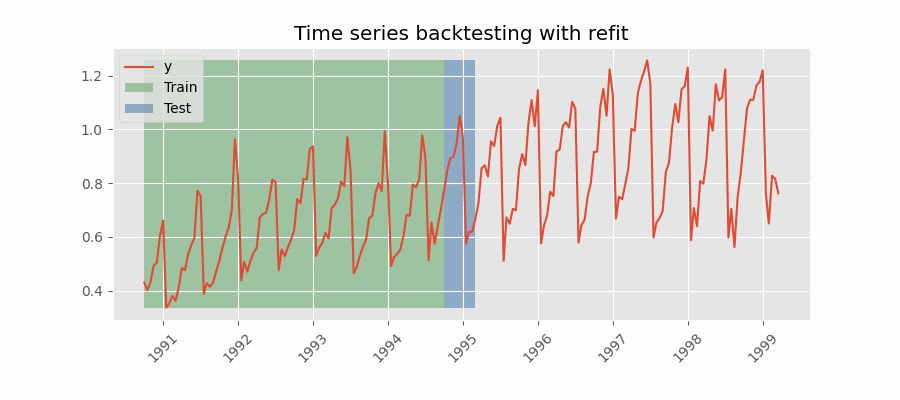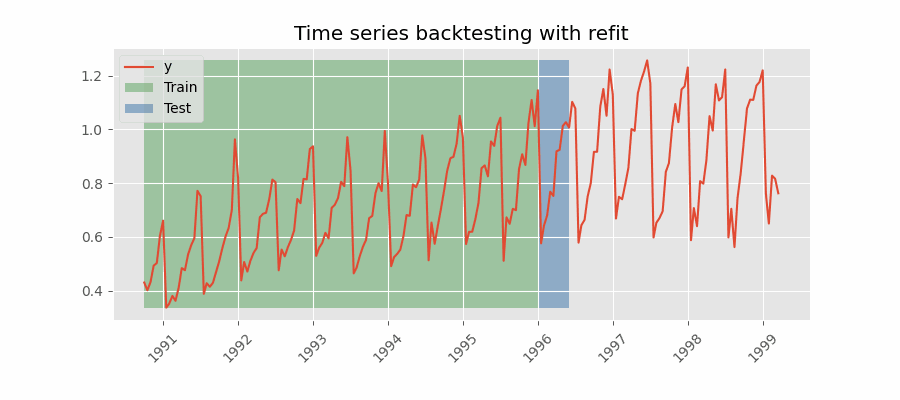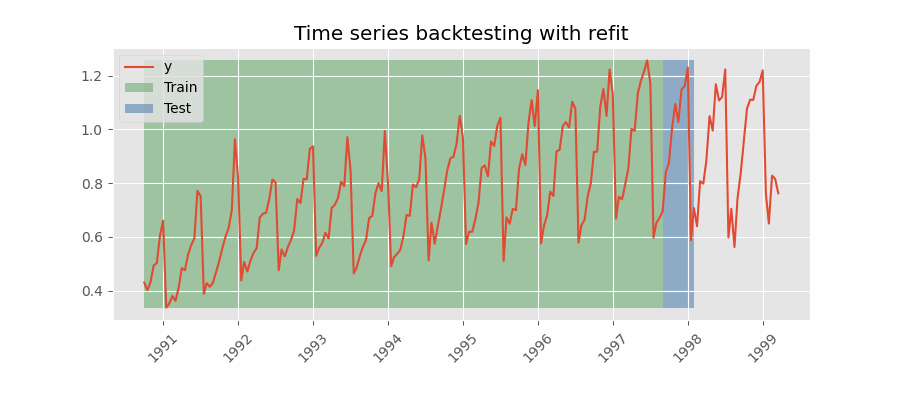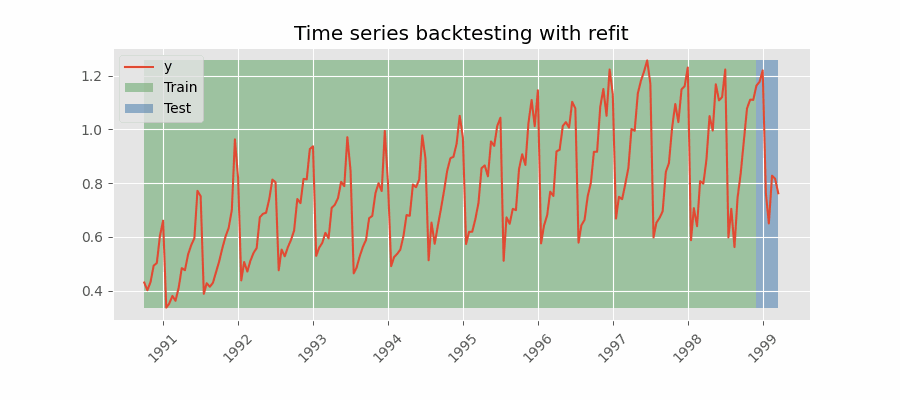
Backtesting with refit and fixed training size (rolling origin)
A technique similar to the previous one but, in this case, the forecast origin rolls forward, therefore, the size of training remains constant. This is also known as time series cross-validation or walk-forward validation.
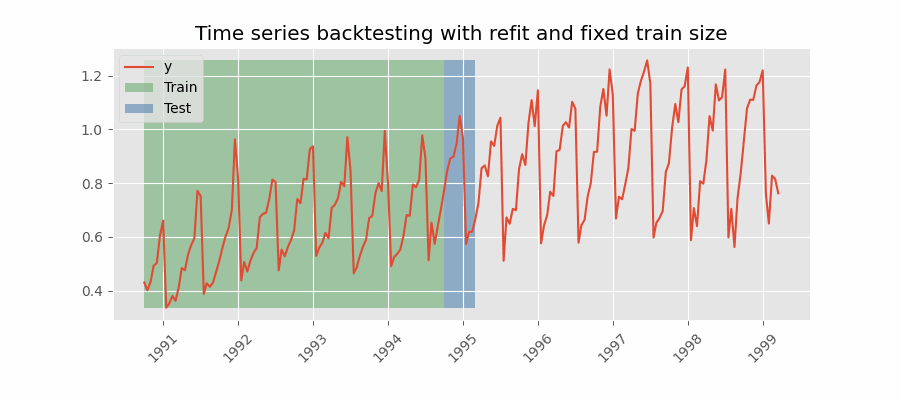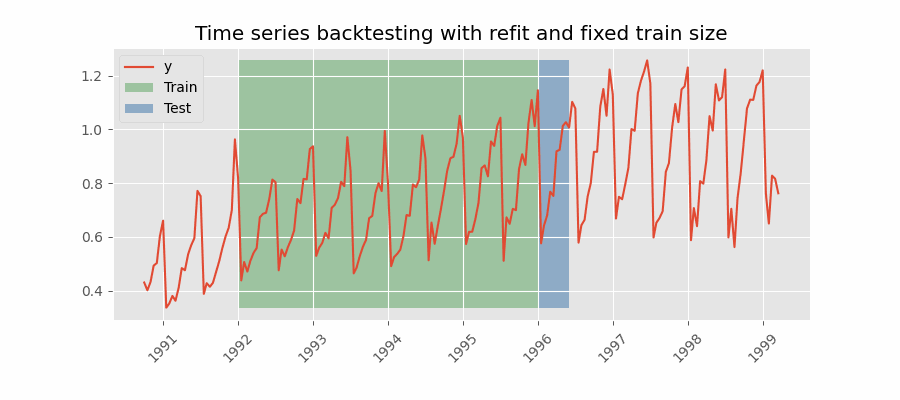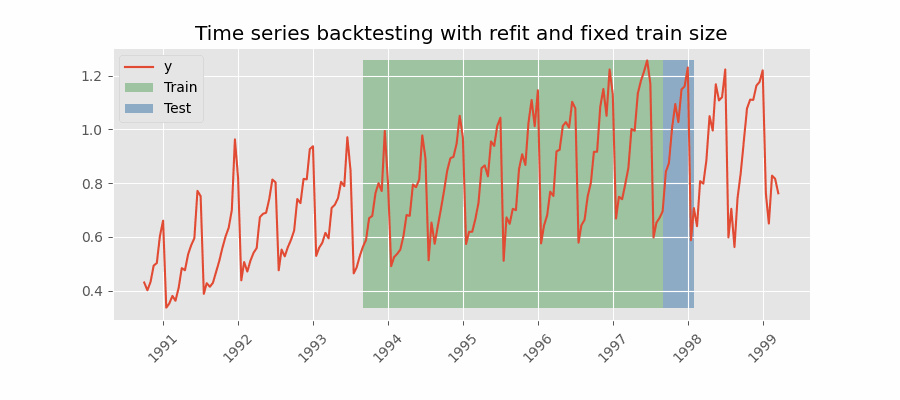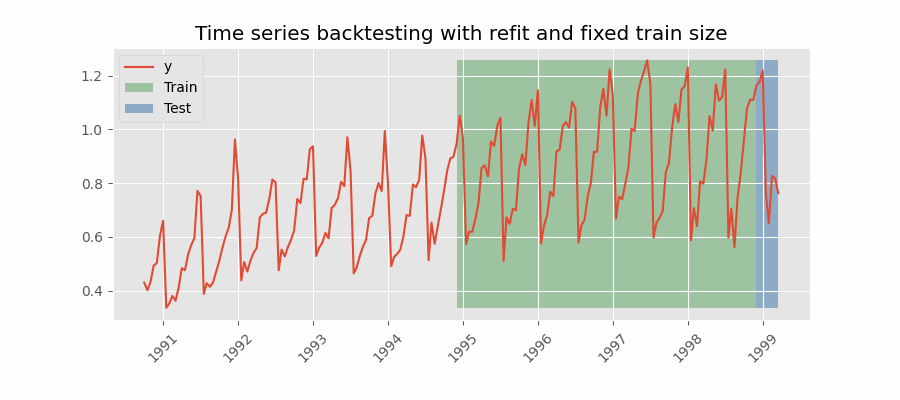
Backtesting with intermittent refit
The model is retrained every $n$ iterations of predictions.
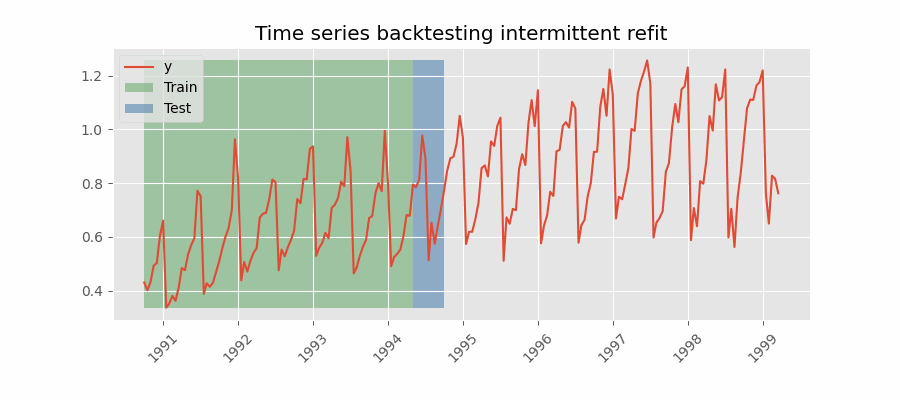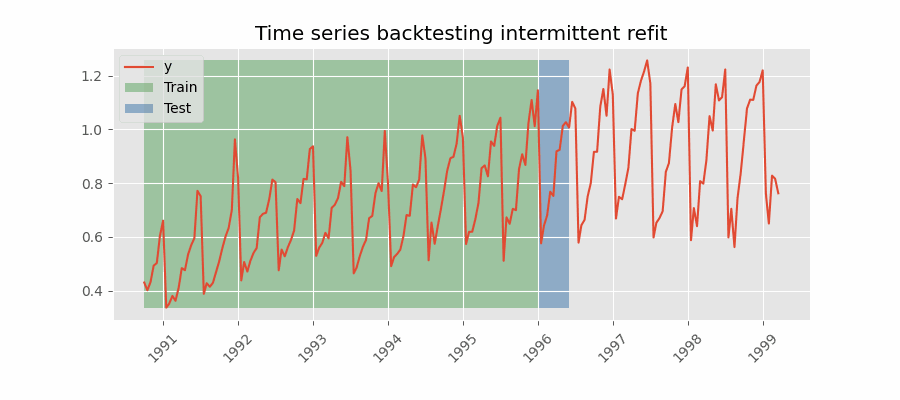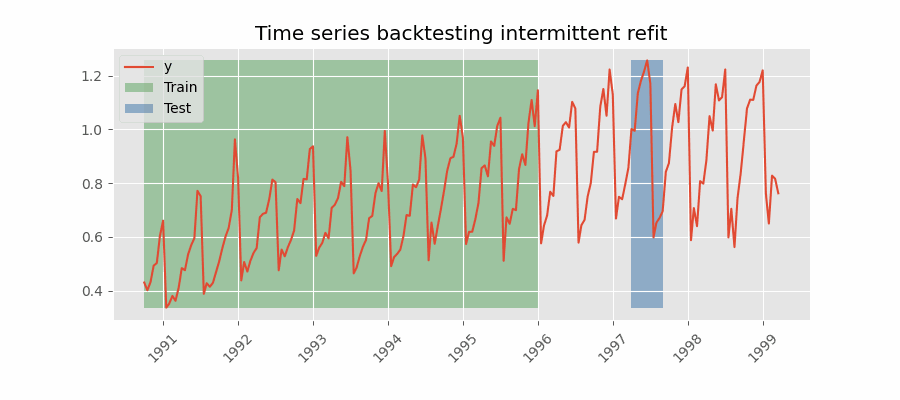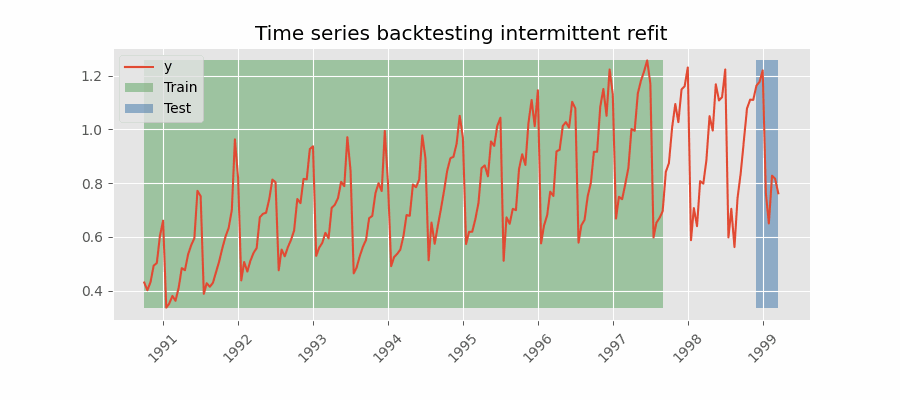
Backtesting without refit
After an initial train, the model is used sequentially without updating it and following the temporal order of the data. This strategy has the advantage of being much faster since the model is trained only once. However, the model does not incorporate the latest information available, so it may lose predictive capacity over time.
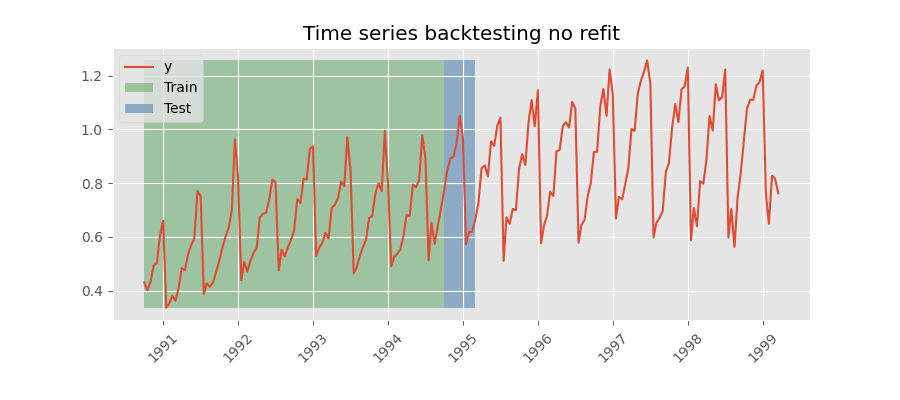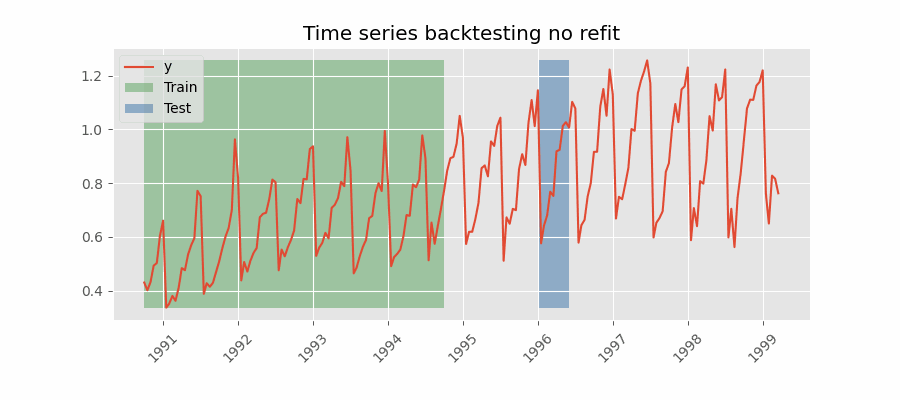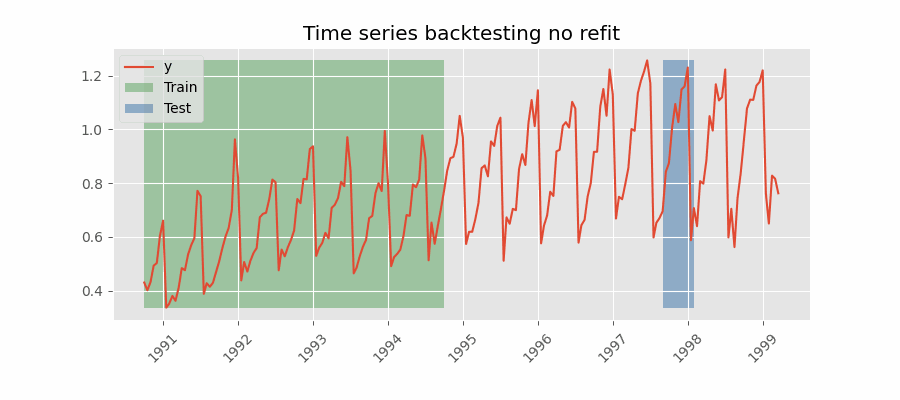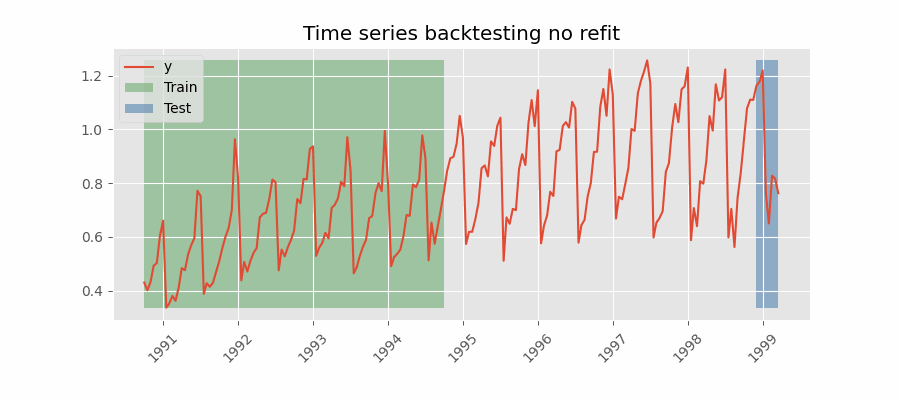
The most appropriate validation method will depend on the strategy to be used in production, whether the model will be periodically retrained or not before the prediction process. Regardless of the strategy used, it is important not to include test data in the search process to avoid overfitting problems.
Libreries¶
Libraries used in this document are:
# Data processing
# ==============================================================================
import numpy as np
import pandas as pd
# Plots
# ==============================================================================
import matplotlib.pyplot as plt
import seaborn as sns
import hvplot.pandas
%matplotlib inline
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
plt.style.use('fivethirtyeight')
plt.rcParams['lines.linewidth'] = 1.5
plt.rcParams['font.size'] = 10
# Modelling and forecasting
# ==============================================================================
from skforecast.ForecasterAutoreg import ForecasterAutoreg
from skforecast.model_selection import grid_search_forecaster
from skforecast.model_selection import backtesting_forecaster
from skforecast.ForecasterSarimax import ForecasterSarimax
from skforecast.model_selection_sarimax import backtesting_sarimax
from skforecast.model_selection_sarimax import grid_search_sarimax
from sklearn.linear_model import Ridge
from sklearn.preprocessing import StandardScaler
from pmdarima import ARIMA
# Warnings config
# ==============================================================================
import warnings
warnings.filterwarnings('ignore')
# Data downloading
# ==============================================================================
url = ('https://raw.githubusercontent.com/JoaquinAmatRodrigo/Estadistica-machine-learning-python/' +
'master/data/visitas_por_dia_web_cienciadedatos.csv')
data = pd.read_csv(url, sep=',')
data.info()
Column date is stored as object. It is converted to datetime type using pd.to_datetime () function. Furthermore, it is set as an index to take advantage of pandas functionalities and finally, its frequency is set to 1 day.
# Data preprocessing
# ==============================================================================
data['date'] = pd.to_datetime(data['date'], format='%d/%m/%y')
data = data.set_index('date')
data = data.asfreq('1D')
data = data.sort_index()
data.head(3)
# Check index is complete or there are missing values
# ==============================================================================
(data.index == pd.date_range(
start = data.index.min(),
end = data.index.max(),
freq = data.index.freq)).all()
print(f"Missing values: {data.isnull().any(axis=1).sum()}")
The data set (starts on 2020-07-01 and ends on 2021-08-22), is divided into 3 partitions: one for training, one for validation and one for testing.
# Split data: train-validation-test
# ==============================================================================
end_train = '2021-03-30 23:59:00'
end_validation = '2021-06-30 23:59:00'
data_train = data.loc[: end_train, :]
data_val = data.loc[end_train:end_validation, :]
data_test = data.loc[end_validation:, :]
print(f"Training dates : {data_train.index.min()} --- {data_train.index.max()} (n={len(data_train)})")
print(f"Validation dates : {data_val.index.min()} --- {data_val.index.max()} (n={len(data_val)})")
print(f"Test dates : {data_test.index.min()} --- {data_test.index.max()} (n={len(data_test)})")
Graphical exploration¶
When working with time series, it is important to represent their values. This allows patterns such as trends and seasonality to be identified.
Time series
# Static plot
# ==============================================================================
# fig, ax = plt.subplots(figsize=(12, 4))
# data_train.users.plot(ax=ax, label='train', linewidth=1)
# data_val.users.plot(ax=ax, label='val', linewidth=1)
# data_test.users.plot(ax=ax, label='test', linewidth=1)
# ax.set_title('Daily visitors')
# ax.legend();
# Interactive plot
# ==============================================================================
plot_train = data_train.users.hvplot.line(label='train')
plot_val = data_val.users.hvplot.line(label='val')
plot_test = data_test.users.hvplot.line(label='test')
layout = plot_train * plot_val * plot_test
layout = layout.opts(title='Daily visitors', ylabel='users')
layout = layout.opts(height=300, width=550)
layout
Seasonality
# Static plot
# ==============================================================================
# fig, ax = plt.subplots(figsize=(7, 3.5))
# data['month'] = data.index.month
# data.boxplot(column='users', by='month', ax=ax,)
# data.groupby('month')['users'].median().plot(style='o-', linewidth=0.8, ax=ax)
# ax.set_ylabel('users')
# ax.set_title('Monthly visitors')
# fig.suptitle('');
# Interactive plot
# ==============================================================================
data['month'] = data.index.month
boxplot = data.sort_values('month').hvplot.box(
y = 'users',
by = 'month',
legend = False,
box_fill_color = None,
outlier_fill_color = None
)
lineplot = data.groupby('month')['users'].median().hvplot.line(legend=False)
scatterplot = data.groupby('month')['users'].median().hvplot.scatter(legend=False)
layout = boxplot * lineplot * scatterplot
layout = layout.opts(title='Monthly visitors', ylabel='users')
layout = layout.opts(height=300, width=500)
layout
# Static plot
# ==============================================================================
# fig, ax = plt.subplots(figsize=(9, 3.5))
# data['month_day'] = pd.Series(data.index).dt.day.values
# data.boxplot(column='users', by='month_day', ax=ax,)
# data.groupby('month_day')['users'].median().plot(style='o-', linewidth=0.8, ax=ax)
# ax.set_ylabel('users')
# ax.set_title('Month-day visitors')
# fig.suptitle('');
# Interactive plot
# ==============================================================================
data['month_day'] = pd.Series(data.index).dt.day.values
boxplot = data.hvplot.box(
y = 'users',
by = 'month_day',
legend = False,
box_fill_color = None,
outlier_fill_color = None
)
lineplot = data.groupby('month_day')['users'].median().hvplot.line(legend=False)
scatterplot = data.groupby('month_day')['users'].median().hvplot.scatter(legend=False)
layout = boxplot * lineplot * scatterplot
layout = layout.opts(title='Month-day visitors', ylabel='users')
layout = layout.opts(height=300, width=500)
layout
# Static plot
# ==============================================================================
# fig, ax = plt.subplots(figsize=(7, 3.5))
# data['week_day'] = data.index.day_of_week + 1
# data.boxplot(column='users', by='week_day', ax=ax)
# data.groupby('week_day')['users'].median().plot(style='o-', linewidth=0.8, ax=ax)
# ax.set_ylabel('users')
# ax.set_title('Week-day visitors')
# fig.suptitle('');
# Interactive plot
# ==============================================================================
data['week_day'] = data.index.day_of_week + 1
boxplot = data.sort_values('week_day').hvplot.box(
y = 'users',
by = 'week_day',
legend = False,
box_fill_color = None,
outlier_fill_color = None
)
lineplot = data.groupby('week_day')['users'].median().hvplot.line(legend=False)
scatterplot = data.groupby('week_day')['users'].median().hvplot.scatter(legend=False)
layout = boxplot * lineplot * scatterplot
layout = layout.opts(title = 'Week-day visitors', ylabel = 'users')
layout = layout.opts(height=300, width=500)
layout
It cannot be determined if there is an annual seasonality since the data does not span two years. However, there is a weekly seasonality, with a reduction in web traffic on weekends.
Autocorrelation plots
# Autocorrelation plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(5, 2))
plot_acf(data.users, ax=ax, lags=50)
plt.show()
# Partial autocorrelation plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(5, 2))
plot_pacf(data.users, ax=ax, lags=50)
plt.show()
Autocorrelation and partial autocorrelation plots show a clear association between the number of users on a day and the previous days. This is an indication that autoregressive models may achive good predictions.
Autoregressive model¶
A autoregressive model (ForecasterAutoreg) is trained using a linear regressor with Ridge regularization, and a time window of 2 weeks (14 lags). The latter means that, for each prediction, the traffic the website had in the previous 14 days is used as predictors.
Ridge models require predictors to be standardized. A StandardScaler is added to the forecaster using the argument transformer_y.
Training Forecaster¶
# Create and train forecaster
# ==============================================================================
forecaster = ForecasterAutoreg(
regressor = Ridge(random_state=123),
lags = 14,
transformer_y = StandardScaler(),
forecaster_id = 'web_traffic'
)
forecaster.fit(y=data_train.users)
forecaster
Prediction (backtest)¶
In order to evaluate the model, it is trained using data from 2020-07-01 to 2021-06-30 and then, predictions are made seven days at a time, without retraining the model. This type of validation is known as backtesting, and can be easily applied with the function backtesting_forecaster ().
# Backtest
# ==============================================================================
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data.users,
initial_train_size = len(data.loc[:end_validation]),
steps = 7,
refit = False,
fixed_train_size = False,
metric = 'mean_absolute_error',
verbose = True,
show_progress = False
)
print(f'Backtest error: {metric}')
predictions.head(5)
# Plot
# ==============================================================================
# fig, ax = plt.subplots(figsize=(10, 3))
# data_test.loc[predictions.index, 'users'].plot(ax=ax, linewidth=2, label='test')
# predictions.plot(linewidth=2, label='prediction', ax=ax)
# ax.set_title('Predictions vs real values')
# ax.legend();
plot_test = data_test.users.hvplot.line(label='test')
plot_predict = predictions.hvplot.line(label='prediction')
layout = plot_test * plot_predict
layout = layout.opts(
title = 'Predictions vs real values',
ylabel = 'users',
legend_position = 'bottom_left'
)
layout = layout.opts(height=300, width=550)
layout
Tuning the hyper-parameters¶
In the previous section, the first 14 lags have been used as predictors and a Ridge model with the default hyperparameters as regressor. However, there is no reason why these values should be the most appropriate.
In order to identify the best combination of lags and hyperparameters, a grid search is used. This process consists of training a model with each combination of hyperparameters-lags, and evaluating its predictive capacity using backtesting. It is important to evaluate the models using only the validation data and not include the test data.
# Grid search of hyper-parameters
# ==============================================================================
forecaster = ForecasterAutoreg(
regressor = Ridge(random_state=123),
lags = 14,
transformer_y = StandardScaler(),
forecaster_id = 'web_traffic'
)
# Regressor's hyper-parameters
param_grid = {'alpha': np.logspace(-3, 3, 10)}
# Lags used as predictors
lags_grid = [7, 14, 21, [7, 14, 21]]
grid_results = grid_search_forecaster(
forecaster = forecaster,
y = data.loc[:end_validation, 'users'],
param_grid = param_grid,
lags_grid = lags_grid,
steps = 7,
metric = 'mean_absolute_error',
refit = False,
initial_train_size = len(data_train),
fixed_train_size = False,
return_best = True,
show_progress = True,
verbose = False
)
# Grid search results
# ==============================================================================
grid_results.head(10)
The best results are obtained using lags [1 2 3 4 5 6 7 8 9 10 11 12 13 14] and a configuration of Ridge {'alpha': 2.154}. By indicating return_best = True in the grid_search_forecaster function, at the end of the process, the forecaster object is automatically retrained with the best configuration and the whole data set.
forecaster
Once the best model has been identified and trained (using both, the training and the validation set), its prediction error is calculated with the test set.
# Backtest final model using test data
# ==============================================================================
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data.users,
initial_train_size = len(data.loc[:end_validation, :]),
steps = 7,
refit = False,
fixed_train_size = False,
metric = 'mean_absolute_error',
show_progress = True,
verbose = False
)
print(f'Backtest error using test data: {metric}')
After optimizing lags and hyperparameters, it has been possible to reduce the prediction error.
ARIMA model¶
SARIMAX (Seasonal Autoregressive Integrated Moving-Average with Exogenous Regressors) is a generalization of the ARIMA model that incorporates both seasonality and exogenous variables. SARIMAX models are among the most widely used statistical forecasting models with excellent forecasting performance.
Skforcast uses the pmdarima implementation of the ARIMA model in conjunction with the ForecasterSarimax class. Validation and optimization can be performed using the backtesting_sarimax() and grid_search_sarimax() functions of the model_selection_sarimax module.
# ForecasterSarimax
# ==============================================================================
forecaster_sarimax = ForecasterSarimax(
regressor = ARIMA(order=(14, 0, 0), maxiter=250),
fit_kwargs = {'disp': 0},
forecaster_id = 'web_traffic_sarimax'
)
# Backtest ARIMA
# ==============================================================================
metric, predictions = backtesting_sarimax(
forecaster = forecaster_sarimax,
y = data.users,
initial_train_size = len(data.loc[:end_validation]),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
verbose = False,
show_progress = True
)
print(f'Backtest error: {metric}')
predictions.head(5)
# fig, ax = plt.subplots(figsize=(10, 3))
# data_test.loc[predictions.index, 'users'].plot(linewidth=2, label='test', ax=ax)
# predictions.plot(linewidth=2, label='prediction', ax=ax)
# ax.set_title('Predictions (ARIMA) vs real values')
# ax.legend();
plot_test = data_test.users.hvplot.line(label='test')
plot_predict = predictions['pred'].hvplot.line(label='prediction')
layout = plot_test * plot_predict
layout = layout.opts(
title = 'Predictions (ARIMA) vs real values',
ylabel = 'users',
legend_position = 'bottom_left'
)
layout = layout.opts(height=300, width=550)
layout
Tuning the hyperparameters¶
Like most models, ARIMA has several hyperparameters that control its behavior:
$p$ is the order (number of time lags) of the autoregressive part of the model.
$d$ is the degree of differencing (the number of times that past values have been subtracted from the data).
$q$ is the order of the moving-average part of the model.
In the pmdarima implementation, these hyperparameters are specified by the order argument. Two good references for more details on ARIMA models are: https://openforecast.org/adam/ARIMA.html and https://otexts.com/fpp3/arima.html.
The grid_search_sarimax function can be used to perform a hyperparameter search by comparing the models according to a metric obtained by backtesting. Check other tuning strategies.
# Grid search of hyperparameters
# ==============================================================================
param_grid = {'order': [(14, 0, 0), (14, 2, 0), (14, 1, 0), (14, 1, 1), (14, 1, 4),
(21, 0, 0), (21, 0, 0), (21, 1, 0), (21, 1, 1), (21, 1, 4)]}
results = grid_search_sarimax(
forecaster = forecaster_sarimax,
y = data.users,
param_grid = param_grid,
initial_train_size = len(data.loc[:end_validation]),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
return_best = True,
verbose = False
)
results
# Backtest final model using test data
# ==============================================================================
metric, predictions = backtesting_sarimax(
forecaster = forecaster_sarimax,
y = data.users,
initial_train_size = len(data.loc[:end_validation]),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
verbose = False,
show_progress = True
)
print(f'Backtest error: {metric}')
Forecasting adding exogenous features¶
In the previous example, only lags of the target variable itself were used as predictors. In certain situations, it is possible to have information on other variables whose future value is known, which can be used as additional predictors in the model. Some typical examples are:
Holidays (local, national...)
Month of the year
Day of the week
Time of day
In this use case, the graphical analysis showed evidence that the number of visits to the website decreases at weekends. The day of the week that each date corresponds to can be known in advance, so it can be used as an exogenous variable. See how it affects the models when this information is included as a predictor.
# Creation of new exogenous features
# ==============================================================================
data = data.drop(columns=['month', 'month_day'])
# One hot encoding of week day
data = pd.get_dummies(data, columns=['week_day'], dtype='int64')
data.head(3)
# Split data train-val-test
# ==============================================================================
data_train = data.loc[: end_train, :]
data_val = data.loc[end_train:end_validation, :]
data_test = data.loc[end_validation:, :]
ForecasterAutoreg¶
# Create and train forecaster
# ==============================================================================
forecaster = ForecasterAutoreg(
regressor = Ridge(alpha=2.15, random_state=123),
lags = 14,
transformer_y = StandardScaler(),
forecaster_id = 'web_traffic'
)
col_exog = [column for column in data.columns if column.startswith(('week'))]
forecaster.fit(y=data_train.users, exog=data_train[col_exog])
# Backtest forecaster with exogenous features
# ==============================================================================
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data.users,
exog = data[col_exog],
initial_train_size = len(data.loc[:end_validation, :]),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
verbose = False,
show_progress = True
)
print(f'Backtest error: {metric}')
predictions.head(5)
ARIMA¶
# ForecasterSarimax
# ==============================================================================
forecaster_sarimax = ForecasterSarimax(
regressor = ARIMA(
order = (21, 1, 1),
seasonal_order = (0,0,0,0),
maxiter = 250
),
fit_kwargs = {'disp': 0},
forecaster_id = 'web_traffic_sarimax'
)
# Backtest ARIMA with exogenous features
# ==============================================================================
metric, predictions = backtesting_sarimax(
forecaster = forecaster_sarimax,
y = data.users,
exog = data[col_exog],
initial_train_size = len(data.loc[:end_validation]),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
verbose = False,
show_progress = True
)
print(f'Backtest error: {metric}')
predictions.head(5)
Prediction intervals¶
Both functions, backtesting_forecaster and backtesting_sarimax, allow obtaining their intervals in addition to the predictions.
# Backtest with prediction intervals
# ==============================================================================
metric, predictions = backtesting_sarimax(
forecaster = forecaster_sarimax,
y = data.users,
exog = data[col_exog],
initial_train_size = len(data.loc[:end_validation]),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
alpha = 0.05,
verbose = False,
show_progress = True
)
print(f'Backtest error: {metric}')
predictions.head(5)
# Static plot
# ==============================================================================
# fig, ax = plt.subplots(figsize=(10, 3))
# data_test.loc[predictions.index, 'users'].plot(linewidth=2, label='test', ax=ax)
# predictions.iloc[:, 0].plot(linewidth=2, label='prediction', ax=ax)
# ax.set_title('Predictions (ARIMA) vs real values')
# ax.fill_between(
# predictions.index,
# predictions.iloc[:, 1],
# predictions.iloc[:, 2],
# alpha = 0.2,
# color = 'red',
# label = 'prediction interval'
# )
# ax.legend();
# Interactive plot
# ==============================================================================
plot_test = data_test.users.hvplot.line(label='test')
plot_predict = predictions['pred'].hvplot.line(label='prediction')
plot_intervalo = predictions.hvplot.area(
y = 'lower_bound',
y2 = 'upper_bound',
color = 'red',
alpha = 0.2,
label = 'prediction interval'
)
layout = plot_intervalo * plot_test * plot_predict
layout = layout.opts(
title = 'Predictions (ARIMA) vs real values',
ylabel = 'users',
legend_position = 'bottom_left'
)
layout = layout.opts(height=300, width=550)
layout
Conclusion¶
The best results are obtained with an ARIMA.
| Model | Exogenous features | MAE backtest |
|---|---|---|
| ARIMA | True | 181.3 |
| ARIMA | False | 181.8 |
| Autoregressive-ridge | True | 195.9 |
| Autoregressive-ridge | False | 216.4 |
How to further improve the model:
Adding as exogenous feature vacation days.
Using non linear regressors such as random forest or gradient boosting Forecasting time series with gradient boosting: Skforecast, XGBoost, LightGBM and CatBoost.
Using a direct multi-step forecaster.
Session information¶
import session_info
session_info.show(html=False)
How to cite this document?
Forecasting web traffic with machine learning and Python by Joaquín Amat Rodrigo and Javier Escobar Ortiz, available under a Attribution 4.0 International (CC BY 4.0) at https://www.cienciadedatos.net/py36-forecasting-visitas-web-machine-learning.html
Did you like the article? Your support is important
Website maintenance has high cost, your contribution will help me to continue generating free educational content. Many thanks! 😊
This work by Joaquín Amat Rodrigo and Javier Escobar Ortiz is licensed under a Creative Commons Attribution 4.0 International License.