Si te gusta Skforecast , ayúdanos dándonos una estrella en GitHub! ⭐️
Intervalos de predicción para modelos de machine learning aplicados a forecasting
⚠ Warning
Ver versión actualizada de este documento en: Forecasting probabilístico con machine learning
Introducción¶
Al tratar de anticipar valores futuros de una serie temporal, la mayoría de los modelos de forecasting intentan predecir cuál será el valor más probable, esto se llama point-forecasting. Aunque conocer de antemano el valor esperado de una serie temporal es útil en casi todos los casos de negocio, este tipo de predicción no proporciona información sobre la confianza del modelo ni sobre la incertidumbre de sus predicciones.
El forecasting probabilístico, a diferencia del point-forecasting, es una familia de técnicas que permiten predecir la distribución esperada de la variable respuesta en lugar de un único valor puntual. Este tipo de forecasting proporciona información muy valiosa ya que permite crear intervalos de predicción, es decir, el rango de valores donde es más probable que pueda estar el valor real. Más formalmente, un intervalo de predicción define el intervalo dentro del cual se espera encontrar el verdadero valor de la variable respuesta con una determinada probabilidad.
Existen múltiples formas de estimar intervalos de predicción en modelos de forecasting, la mayoría de las cuales requieren que los residuos (errores) del modelo sigan una distribución normal. Cuando no se puede asumir esta propiedad, dos alternativas comúnmente utilizadas son el bootstrapping y la regresión cuantílica. Para ilustrar cómo la librería skforecast permite estimar intervalos de predicción en modelos de forecasting multi-step se intenta predecir la demanda de energía para un horizonte de 7 días. Se utilizan dos estrategias diferentes:
Intervalos de predicción basados en bootstrapping para un modelo de tipo recursive-multi-step forecaster.
Intervalos de predicción basados en regresión cuantílica para un modelo de tipo direct-multi-step forecaster.
⚠ Warning
Tal y como describe Rob J Hyndman en su blog, en los casos reales, casi todos los intervalos de predicción resultan ser demasiado estrechos. Por ejemplo, intervalos teóricos del 95% solo suelen conseguir una cobertura real de entre el 71% y el 87%. Este fenómeno surge debido a que estos intervalos no contemplan todas las fuentes de incertidumbre que, en el caso de modelos de *forecasting*, suelen ser de 4 tipos:- El término de error aleatorio
- Las estimación de parámetros
- La elección del modelo
- El proceso de predicción de valores futuros
🖉 Note
Si es la primera vez que usa skforecast, visite Skforecast: forecasting de series temporales con Python y Scikit-learn para una introducción rápida.Intervalos de predicción utilizando bootstrapping de los residuos¶
El error en la predicción del siguiente valor de una serie (one-step-ahead forecast) se define como $e_t = y_t - \hat{y}_{t|t-1}$. Asumiendo que los errores futuros serán similares a los errores pasados, es posible simular diferentes predicciones tomando muestras de los errores vistos previamente en el pasado (es decir, los residuos) y agregándolos a las predicciones.
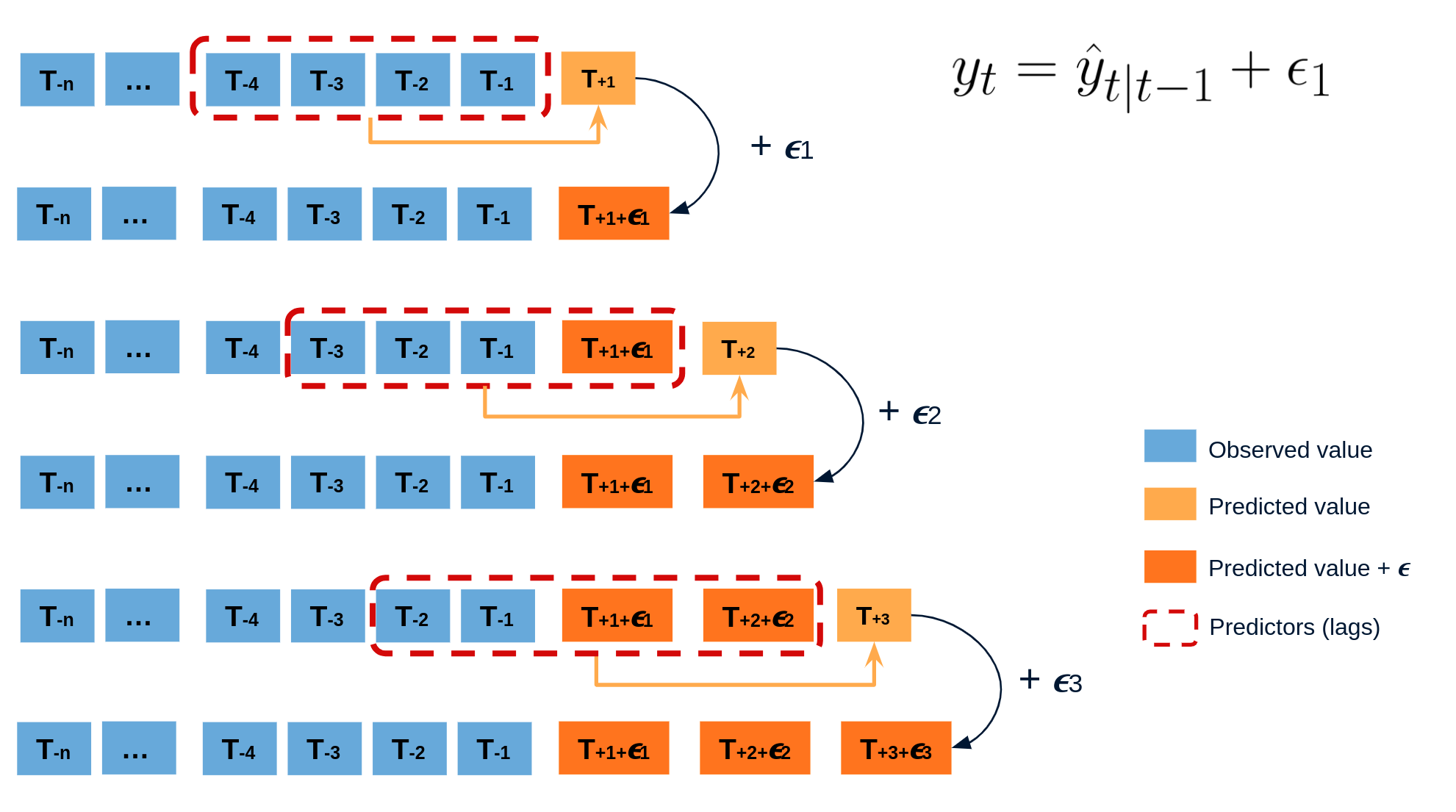
Al hacer esto repetidamente, se crea una colección de predicciones ligeramente diferentes (posibles caminos futuros), que representan la varianza esperada en el proceso de forecasting.
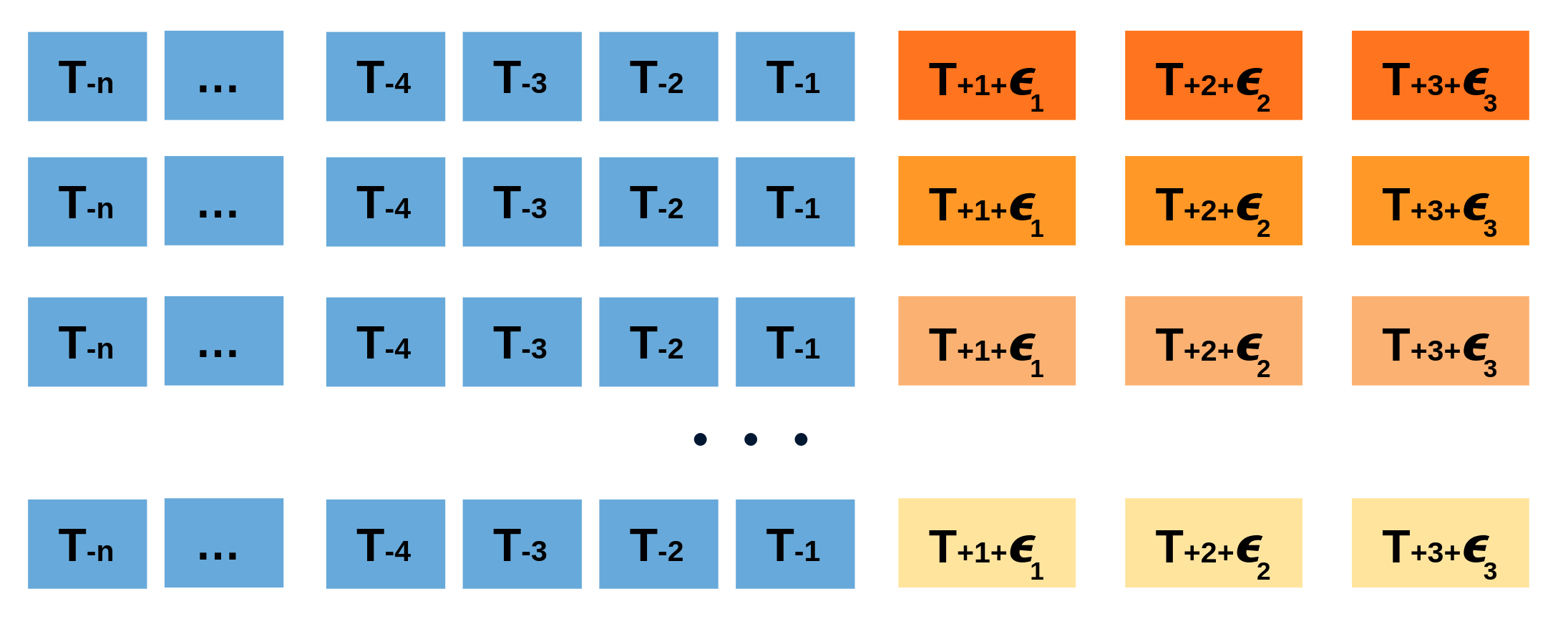
Finalmente, los intervalos de predicción se crean calculando los percentiles $\alpha/2$ y $1−\alpha/2$ de los datos simulados en cada horizonte de predicción.
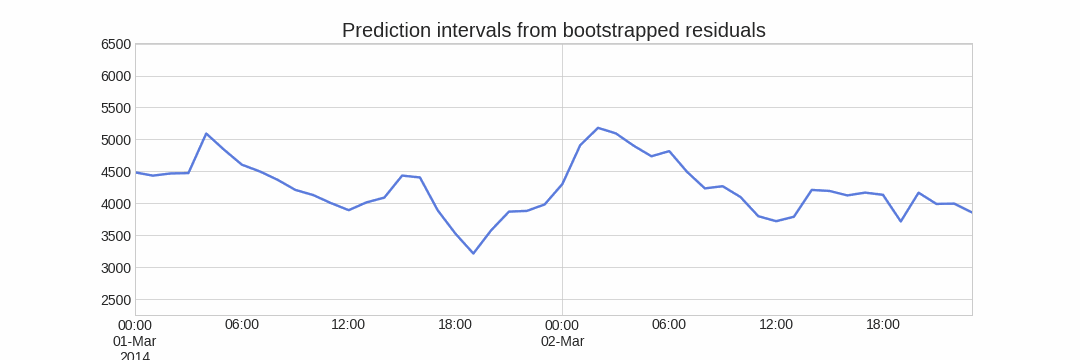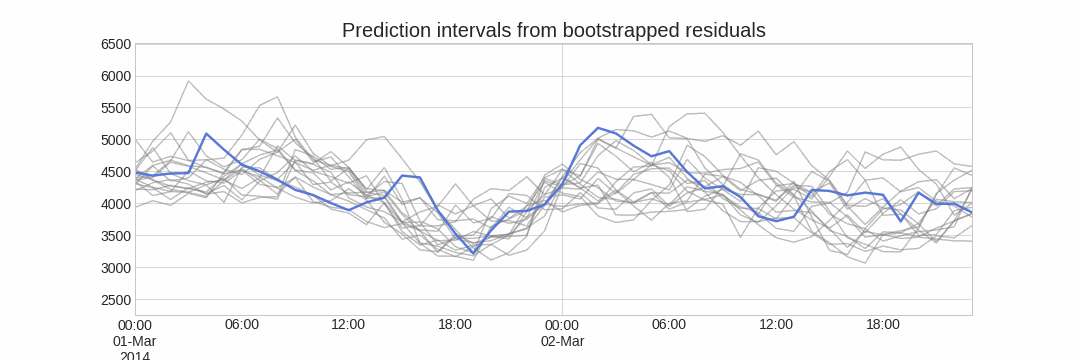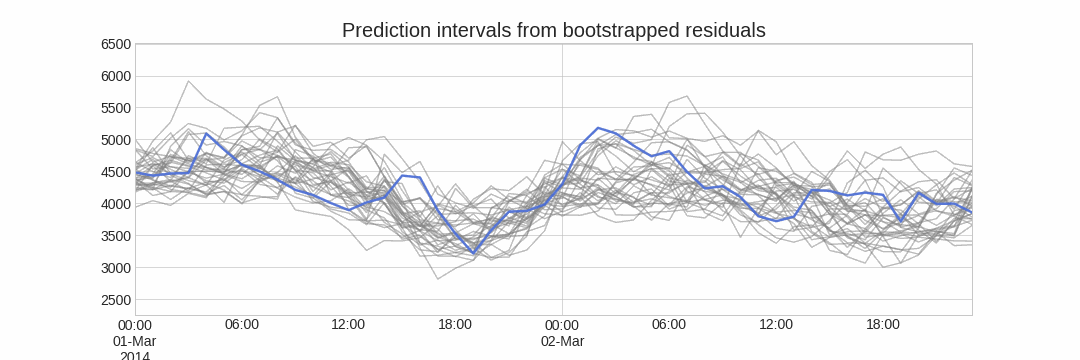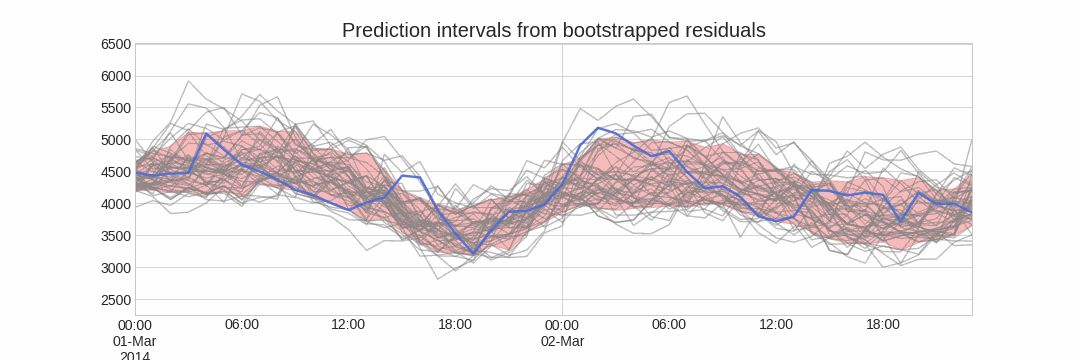
La principal ventaja de esta estrategia es que solo requiere de un único modelo para estimar cualquier intervalo. El inconveniente es la necesidad de ejecutar cientos o miles de iteraciones de bootstrapping lo cual resulta muy costoso desde el punto de vista computacional y no siempre es posible.
Este tipo de intervalos de predicción se pueden estimar fácilmente utilizando ForecasterAutoreg y ForecasterAutoregCustom.
Intervalos de predicción utilizando modelos de regresión cuantílica¶
A diferencia de los modelos de regresión más comunes, que pretende estimar la media de la variable respuesta dados ciertos valores de las variables predictoras, la regresión cuantílica tiene como objetivo estimar los cuantiles condicionales de la variable respuesta. Para una función de distribución continua, el cuantil $\alpha$ $Q_{\alpha}(x)$ se define como el valor tal que la probabilidad de que $Y$ sea menor que $Q_{\alpha}(x)$ es, para un determinado $X=x$, igual a $\alpha$. Por ejemplo, el 36% de los valores de la población son inferiores al cuantil $Q=0,36$. El cuantil más conocido es el cuantil 50%, más comúnmente conocido como mediana.
Al combinar las predicciones de dos modelos de regresión cuantílica, es posible construir un intervalo donde, cada modelo, estima uno de los límites del intervalo. Por ejemplo, los modelos obtenidos para $Q = 0.1$ y $Q = 0.9$ generan un intervalo de predicción del 80% (90% - 10% = 80%).
Son varios los algoritmos de machine learning capaces de modelar cuantiles. Algunos de ellos son:
Así como el error cuadrático se utiliza como función de coste para entrenar modelos que predicen el valor medio, se necesita una función de coste específica para entrenar modelos que predicen cuantiles. La función utilizada con más frecuencia para la regresión de cuantiles se conoce como pinball:
$$\text{pinball}(y, \hat{y}) = \frac{1}{n_{\text{muestras}}} \sum_{i=0}^{n_{\text{muestras}}- 1} \alpha \max(y_i - \hat{y}_i, 0) + (1 - \alpha) \max(\hat{y}_i - y_i, 0)$$donde $\alpha$ es el cuantil objetivo, $y$ el valor real e $\hat{y}$ la predicción del cuantil.
Se puede observar que el coste difiere según el cuantil evaluado. Cuanto mayor sea el cuantil, más se penalizan las subestimaciones y menos las sobreestimaciones. Al igual que con MSE y MAE, el objetivo es minimizar sus valores (a menor coste, mejor).
Dos desventajas de la regresión por cuantiles en comparación con el método de bootstrapping son: que cada cuantil necesita su regresor, y que la regresión por cuantiles no está disponible para todos los tipos de modelos de regresión. Sin embargo, una vez entrenados los modelos, la inferencia es mucho más rápida ya que no se necesita un proceso iterativo.
Este tipo de intervalos de predicción se pueden estimar fácilmente utilizando ForecasterAutoregDirect.
Librerías¶
Librerías utilizadas en este documento
# Preprocesado de datos
# ==============================================================================
import numpy as np
import pandas as pd
# Plots
# ==============================================================================
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from statsmodels.graphics.tsaplots import plot_acf
import plotly.express as px
import plotly.graph_objects as go
plt.style.use('fivethirtyeight')
plt.rcParams['lines.linewidth'] = 1.5
dark_style = {
'figure.facecolor' : '#212946',
'axes.facecolor' : '#212946',
'savefig.facecolor' : '#212946',
'axes.grid' : True,
'axes.grid.which' : 'both',
'axes.spines.left' : False,
'axes.spines.right' : False,
'axes.spines.top' : False,
'axes.spines.bottom': False,
'grid.color' : '#2A3459',
'grid.linewidth' : '1',
'text.color' : '0.9',
'axes.labelcolor' : '0.9',
'xtick.color' : '0.9',
'ytick.color' : '0.9',
'font.size' : 12
}
plt.rcParams.update(dark_style)
# Modelado y Forecasting
# ==============================================================================
from lightgbm import LGBMRegressor
import sklearn.linear_model
from skforecast.ForecasterAutoreg import ForecasterAutoreg
from skforecast.ForecasterAutoregDirect import ForecasterAutoregDirect
from skforecast.model_selection import grid_search_forecaster
from skforecast.model_selection import backtesting_forecaster
from sklearn.metrics import mean_pinball_loss
# Configuración
# ==============================================================================
import warnings
warnings.filterwarnings('once')
Data¶
Los datos utilizados en este documento se han obtenido del paquete de R tsibbledata. El conjunto de datos contiene la demanda de electricidad cada 30 minutos del estado de Victoria (Australia), junto con información adicional sobre la temperatura y un indicador de si ese día es festivo. En los siguientes ejemplos, los datos se agregan a nivel diario.
# Descarga de datos
# ==============================================================================
url = ('https://raw.githubusercontent.com/JoaquinAmatRodrigo/skforecast/master/' +
'data/vic_elec.csv')
data = pd.read_csv(url, sep=',')
# Preprocesado de datos (agregación a frecuencia diaria)
# ==============================================================================
data['Time'] = pd.to_datetime(data['Time'], format='%Y-%m-%dT%H:%M:%SZ')
data = data.set_index('Time')
data = data.asfreq('30min')
data = data.sort_index()
data = data.drop(columns='Date')
data = data.resample(rule='D', closed='left', label ='right')\
.agg({'Demand': 'sum', 'Temperature': 'mean', 'Holiday': 'max'})
data.head()
# Partición de datos en entrenamiento-validación-test
# ==============================================================================
data = data.loc['2012-01-01 00:00:00': '2014-12-30 23:00:00']
end_train = '2013-12-31 23:59:00'
end_validation = '2014-9-30 23:59:00'
data_train = data.loc[: end_train, :].copy()
data_val = data.loc[end_train:end_validation, :].copy()
data_test = data.loc[end_validation:, :].copy()
print(f"Fechas entrenamiento : {data_train.index.min()} --- {data_train.index.max()} (n={len(data_train)})")
print(f"Fechas validación : {data_val.index.min()} --- {data_val.index.max()} (n={len(data_val)})")
print(f"Fechas test : {data_test.index.min()} --- {data_test.index.max()} (n={len(data_test)})")
# Gráfico de la serie temporal
# ==============================================================================
fig, ax=plt.subplots(figsize=(8, 4))
data_train['Demand'].plot(label='train', ax=ax)
data_val['Demand'].plot(label='validation', ax=ax)
data_test['Demand'].plot(label='test', ax=ax)
ax.yaxis.set_major_formatter(ticker.EngFormatter())
ax.set_ylim(bottom=160_000)
ax.set_ylabel('MW')
ax.set_title('Demanda de energía')
ax.legend();
# Gráfico interactivo de la serie temporal
# ==============================================================================
# data.loc[:end_train, 'partition'] = 'train'
# data.loc[end_train:end_validation, 'partition'] = 'validation'
# data.loc[end_validation:, 'partition'] = 'test'
# fig = px.line(
# data_frame = data.iloc[1:, :].reset_index(),
# x = 'Time',
# y = 'Demand',
# color = 'partition',
# title = 'Demanda energía',
# width = 900,
# height = 500
# )
# fig.update_xaxes(
# rangeslider_visible=True,
# rangeselector=dict(
# buttons=list([
# dict(count=1, label="1m", step="month", stepmode="backward"),
# dict(count=6, label="6m", step="month", stepmode="backward"),
# dict(count=1, label="YTD", step="year", stepmode="todate"),
# dict(count=1, label="1y", step="year", stepmode="backward"),
# dict(step="all")
# ])
# )
# )
# fig.show()
# data=data.drop(columns='partition')
# Gráfico de autocorrelación
# ==============================================================================
fig, ax = plt.subplots(figsize=(5, 2))
plot_acf(data.Demand, ax=ax, lags=30)
plt.show()
Teniendo en cuenta el gráfico de autocorrelación, el valor de la demanda de los últimos 7 días podría ser un buen predictor.
Intervalos de predicción basados en bootstrapping¶
Se entrena un recursive-multi-step forecaster y se optimizan sus hiperparámetros. Luego, se estiman los intervalos de predicción utilizando bootstrapping.
# Crear forecaster
# ==============================================================================
forecaster = ForecasterAutoreg(
regressor = LGBMRegressor(random_state=123),
lags = 7
)
forecaster
In order to find the best value for the hyper-parameters, a grid search is carried out. It is important not to include test data in the search, otherwise model overfitting could happen.
# Grid search de hyper-parámetros y lags
# ==============================================================================
# Hyper-parámetros del regresor
param_grid = {
'n_estimators': [100, 500],
'max_depth': [3, 5, 10],
'learning_rate': [0.01, 0.1]
}
# Lags utilizados como predictores
lags_grid = [7]
results_grid_q10 = grid_search_forecaster(
forecaster = forecaster,
y = data.loc[:end_validation, 'Demand'],
param_grid = param_grid,
lags_grid = lags_grid,
steps = 7,
refit = False,
metric = 'mean_squared_error',
initial_train_size = int(len(data_train)),
fixed_train_size = False,
return_best = True,
verbose = False,
show_progress = True
)
Una vez encontrados los mejores hiperparámetros, se aplica un proceso de backtesting para evaluar el desempeño del modelo sobre los datos de test y calcular la cobertura real del intervalo estimado.
# Backtesting
# ==============================================================================
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
initial_train_size = len(data_train) + len(data_val),
fixed_train_size = False,
steps = 7,
refit = False,
interval = [10, 90],
n_boot = 1000,
metric = 'mean_squared_error',
verbose = False,
show_progress = True
)
predictions.head(4)
# Cobertura del intervalo en los datos de test
# ==============================================================================
inside_interval = np.where(
(data.loc[predictions.index, 'Demand'] >= predictions['lower_bound']) & \
(data.loc[predictions.index, 'Demand'] <= predictions['upper_bound']),
True,
False
)
coverage = inside_interval.mean()
print(f"Cobertura del intervalo predicho con los datos de test: {100 * coverage}")
La cobertura del intervalo predicho (71%) es inferior a la esperada (80%).
# Gráfico
# ==============================================================================
fig, ax=plt.subplots(figsize=(8, 3))
data.loc[end_validation:, 'Demand'].plot(ax=ax, label='Demand', linewidth=3, color="#23b7ff")
ax.fill_between(
predictions.index,
predictions['lower_bound'],
predictions['upper_bound'],
color = 'deepskyblue',
alpha = 0.3,
label = '80% interval'
)
ax.yaxis.set_major_formatter(ticker.EngFormatter())
ax.set_ylabel('MW')
ax.set_title('Predicción de la demanda energética')
ax.legend();
# Gráfico interactivo
# ==============================================================================
# fig = px.line(
# data_frame = data.loc[end_validation:, 'Demand'].reset_index(),
# x = 'Time',
# y = 'Demand',
# title = 'Predicción de la demanda energética',
# width = 900,
# height = 500
# )
# fig.add_traces([
# go.Scatter(
# x = predictions.index,
# y = predictions['lower_bound'],
# mode = 'lines',
# line_color = 'rgba(0,0,0,0)',
# showlegend = False
# ),
# go.Scatter(
# x = predictions.index,
# y = predictions['upper_bound'],
# mode = 'lines',
# line_color = 'rgba(0,0,0,0)',
# fill='tonexty',
# fillcolor = 'rgba(255, 0, 0, 0.2)',
# showlegend = False
# )]
# )
# fig.show()
Por defecto, se utilizan los residuos de entrenamiento para estimar los intervalos de predicción. Sin embargo, se pueden utilizar otros residuos, por ejemplo, los obtenidos a partir de un conjunto de validación.
Para hacer esto, los nuevos residuos deben almacenarse dentro del forecaster usando el método set_out_sample_residuals. Una vez que se hayan agregado los nuevos residuales al forecaster, solo hay que indicar in_sample_residuals = False cuando se usa el método predict_interval.
Modelos de regresión por cuantiles¶
Al igual que en el ejemplo anterior, se estima un intervalo de predicción del 80% para los siguientes 7 días pero, esta vez, utilizando la estrategia de regresión por cuantiles. En este ejemplo, se entrena un modelo de gradient boosting LightGBM, sin embargo, el lector puede utilizar cualquier otro modelo simplemente reemplazando la definición del regresor.
# Crear forecasters: uno para cada límite del intervalo
# ==============================================================================
# Los forecasters obtenidos para alpha=0.1 y alpha=0.9 producen un intervalo de
# confianza del 80% (90% - 10% = 80%).
# Forecaster para cuantil 10%
forecaster_q10 = ForecasterAutoregDirect(
regressor = LGBMRegressor(
objective = 'quantile',
metric = 'quantile',
alpha = 0.1,
learning_rate = 0.1,
max_depth = 10,
n_estimators = 100,
random_state = 123
),
lags = 7,
steps = 7
)
# Forecaster para cuantil 90%
forecaster_q90 = ForecasterAutoregDirect(
regressor = LGBMRegressor(
objective = 'quantile',
metric = 'quantile',
alpha = 0.9,
learning_rate = 0.1,
max_depth = 10,
n_estimators = 100,
random_state = 123
),
lags = 7,
steps = 7
)
Al validar un modelo de regresión por cuantiles, se debe proporcionar una métrica personalizada según el cuantil que se esté estimando. Estas mismas métricas se volverán a utilizar al ajustar los hiperparámetros de cada modelo.
# Función de coste para cada cuantil (pinball_loss)
# ==============================================================================
def mean_pinball_loss_q10(y_true, y_pred):
"""
Pinball loss for quantile 10.
"""
return mean_pinball_loss(y_true, y_pred, alpha=0.1)
def mean_pinball_loss_q90(y_true, y_pred):
"""
Pinball loss for quantile 90.
"""
return mean_pinball_loss(y_true, y_pred, alpha=0.9)
# Backtesting con datos de test
# ==============================================================================
metric_q10, predictions_q10 = backtesting_forecaster(
forecaster = forecaster_q10,
y = data['Demand'],
initial_train_size = len(data_train) + len(data_val),
fixed_train_size = False,
steps = 7,
refit = False,
metric = mean_pinball_loss_q10,
verbose = False
)
metric_q90, predictions_q90 = backtesting_forecaster(
forecaster = forecaster_q90,
y = data['Demand'],
initial_train_size = len(data_train) + len(data_val),
fixed_train_size = False,
steps = 7,
refit = False,
metric = mean_pinball_loss_q90,
verbose = False
)
Las predicciones generadas por cada modelo se utilizan para definir los límites superior e inferior del intervalo.
# Cobertura del intervalo en los datos de test
# ==============================================================================
inside_interval = np.where(
(data.loc[end_validation:, 'Demand'] >= predictions_q10['pred']) & \
(data.loc[end_validation:, 'Demand'] <= predictions_q90['pred']),
True,
False
)
coverage = inside_interval.mean()
print(f"Cobertura del intervalo predicho con los datos de test: {100 * coverage}")
La cobertura real del intervalo predicho (56%) es muy inferior a la esperada (80%).
Los hiperparámetros del modelo anterior se elegieron sin un criterio concreto, además no hay motivo por el que los mismos hiperparámetros sean adecuados para los diferentes cuantiles. Se lleva a cabo una búsqueda grid search para cada forecaster.
# Grid search para los hyper-parámetros y lags de cada quantile-forecaster
# ==============================================================================
# Hyper-parametros del regresor
param_grid = {
'n_estimators': [100, 500],
'max_depth': [3, 5, 10],
'learning_rate': [0.01, 0.1]
}
# Lags utilizados como predictores
lags_grid = [7]
results_grid_q10 = grid_search_forecaster(
forecaster = forecaster_q10,
y = data.loc[:end_validation, 'Demand'],
param_grid = param_grid,
lags_grid = lags_grid,
steps = 7,
refit = False,
metric = mean_pinball_loss_q10,
initial_train_size = int(len(data_train)),
fixed_train_size = False,
return_best = True,
verbose = False,
show_progress = False
)
results_grid_q90 = grid_search_forecaster(
forecaster = forecaster_q90,
y = data.loc[:end_validation, 'Demand'],
param_grid = param_grid,
lags_grid = lags_grid,
steps = 7,
refit = False,
metric = mean_pinball_loss_q90,
initial_train_size = int(len(data_train)),
fixed_train_size = False,
return_best = True,
verbose = False,
show_progress = False
)
Una vez que se han encontrado los mejores hiperparámetros para cada forecaster, se aplica nuevamente un proceso de backtesting utilizando los datos de test.
# Backtesting con datos de test
# ==============================================================================
metric_q10, predictions_q10 = backtesting_forecaster(
forecaster = forecaster_q10,
y = data['Demand'],
initial_train_size = len(data_train) + len(data_val),
fixed_train_size = False,
steps = 7,
refit = False,
metric = mean_pinball_loss_q10,
verbose = False
)
metric_q90, predictions_q90 = backtesting_forecaster(
forecaster = forecaster_q90,
y = data['Demand'],
initial_train_size = len(data_train) + len(data_val),
fixed_train_size = False,
steps = 7,
refit = False,
metric = mean_pinball_loss_q90,
verbose = False
)
# Gráfico
# ==============================================================================
fig, ax=plt.subplots(figsize=(8, 3))
data.loc[end_validation:, 'Demand'].plot(ax=ax, label='Demand', linewidth=3, color="#23b7ff")
ax.fill_between(
data.loc[end_validation:].index,
predictions_q10['pred'],
predictions_q90['pred'],
color = 'deepskyblue',
alpha = 0.3,
label = '80% interval'
)
ax.yaxis.set_major_formatter(ticker.EngFormatter())
ax.set_ylabel('MW')
ax.set_title('Predicción de la demanda energética')
ax.legend();
# Cobertura del intervalo en los datos de test
# ==============================================================================
inside_interval = np.where(
(data.loc[end_validation:, 'Demand'] >= predictions_q10['pred']) & \
(data.loc[end_validation:, 'Demand'] <= predictions_q90['pred']),
True,
False
)
coverage = inside_interval.mean()
print(f"Cobertura del intervalo predicho con los datos de test: {100 * coverage}")
Tras optimizar los hiperparámetros de cada forecaster la cobertura se acerca más a la esperada (80%).
Información de sesión¶
import session_info
session_info.show(html=False)
¿Cómo citar este documento?
Intervalos de predicción para modelos de machine learning aplicados a forecasting por Joaquín Amat Rodrigo and Javier Escobar Ortiz, disponible con licencia CC BY-NC-SA 4.0 en https://www.cienciadedatos.net/documentos/py42-forecasting-probabilistico.html
¿Te ha gustado el artículo? Tu ayuda es importante
Mantener un sitio web tiene unos costes elevados, tu contribución me ayudará a seguir generando contenido divulgativo gratuito. ¡Muchísimas gracias! 😊
Este contenido, creado por Joaquín Amat Rodrigo y Javier Escobar Ortiz, tiene licencia Attribution-NonCommercial-ShareAlike 4.0 International.
Se permite:
-
Compartir: copiar y redistribuir el material en cualquier medio o formato.
-
Adaptar: remezclar, transformar y crear a partir del material.
Bajo los siguientes términos:
-
Atribución: Debes otorgar el crédito adecuado, proporcionar un enlace a la licencia e indicar si se realizaron cambios. Puedes hacerlo de cualquier manera razonable, pero no de una forma que sugiera que el licenciante te respalda o respalda tu uso.
-
NoComercial: No puedes utilizar el material para fines comerciales.
-
CompartirIgual: Si remezclas, transformas o creas a partir del material, debes distribuir tus contribuciones bajo la misma licencia que el original.