Más sobre ciencia de datos en: cienciadedatos.net
- Regresión lineal con Python
- Regresión lineal múltiple con Python
- Regresión logística con Python
- Regularización Ridge, Lasso y Elastic Net con Python
- Machine learning con Python y Scikitlearn
- Árboles de decisión con Python: regresión y clasificación
- Random Forest con Python y Scikit-learn
- Gradient Boosting con Python y Scikit-learn
- Gradient Boosting probabilístico con Python
- Máquinas de Vector Soporte (SVM)
- Redes neuronales con Python
- Análisis de componentes principales PCA
- Clustering
- Detección de anomalías con PCA
- Detección de anomalías con autoencoders
- Detección de anomalías con Gaussian Mixture Models
- Detección de anomalías con Isolation Forest
- Análisis de texto (text mining) con Python
- Reglas de asociación

Introducción¶
La detección de anomalías (outliers) con autoencoders es una estrategia no supervisada para identificar anomalías cuando los datos no están etiquetados, es decir, no se conoce la clasificación real (anomalía - no anomalía) de las observaciones.
Si bien esta estrategia hace uso de autoencoders, no utiliza directamente su resultado como forma de detectar anomalías, sino que emplea el error de reconstrucción producido al revertir la reducción de dimensionalidad. El error de reconstrucción como estrategia para detectar anomalías se basa en la siguiente idea: los métodos de reducción de dimensionalidad permiten proyectar las observaciones en un espacio de menor dimensión que el espacio original, a la vez que tratan de conservar la mayor información posible. La forma en que consiguen minimizar la pérdida global de información es buscando un nuevo espacio en el que la mayoría de observaciones puedan ser bien representadas.
El método autoencoders crea una función que mapea la posición que ocupa cada observación en el espacio original con el que ocupa en el nuevo espacio generado. Este mapeo funciona en ambas direcciones, por lo que también se puede ir desde el nuevo espacio al espacio original. Solo aquellas observaciones que hayan sido bien proyectadas podrán volver a la posición que ocupaban en el espacio original con una precisión elevada.
Dado que la búsqueda de ese nuevo espacio ha sido guiada por la mayoría de las observaciones, serán las observaciones más próximas al promedio las que mejor puedan ser proyectadas y en consecuencia mejor reconstruidas. Las observaciones anómalas, por el contrario, serán mal proyectadas y su reconstrucción será peor. Es este error de reconstrucción (elevado al cuadrado) el que puede emplearse para identificar anomalías.
La detección de anomalías con autoencoders es muy similar a la detección de anomalías con PCA. La diferencia reside en que, el PCA, solo es capaz de aprender transformaciones lineales, mientras que los autoencoders no tienen esta restricción y pueden aprender transformaciones no lineales.
Autoencoders en python
En Python, los autoencoders se implementan principalmente utilizando bibliotecas de deep learning como TensorFlow-Keras y PyTorch, que permiten definir arquitecturas personalizadas adaptadas a distintos tipos de datos y objetivos. Además, existen librerías de más alto nivel como H2O y PyOD, que ofrecen implementaciones de autoencoders ya configuradas para tareas específicas —como la detección de anomalías— sin que el usuario tenga que diseñar y entrenar la arquitectura desde cero.
Autoencoders¶
Los autoencoders son un tipo de redes neuronales en las que la entrada y salida del modelo es la misma, es decir, redes entrenadas para predecir un resultado igual a los datos de entrada. Para conseguir este tipo de comportamiento, la arquitectura de los autoencoders suele ser simétrica, con una región llamada encoder y otra decoder. ¿Cómo sirve esto para reducir la dimensionalidad? Los autoencoders siguen una arquitectura de cuello de botella, la región encoder está formada por una o varias capas, cada una con menos neuronas que su capa precedente, obligando así a que la información de entrada se vaya comprimiendo. En la región decoder esta compresión se revierte siguiendo la misma estructura pero esta vez de menos a más neuronas.
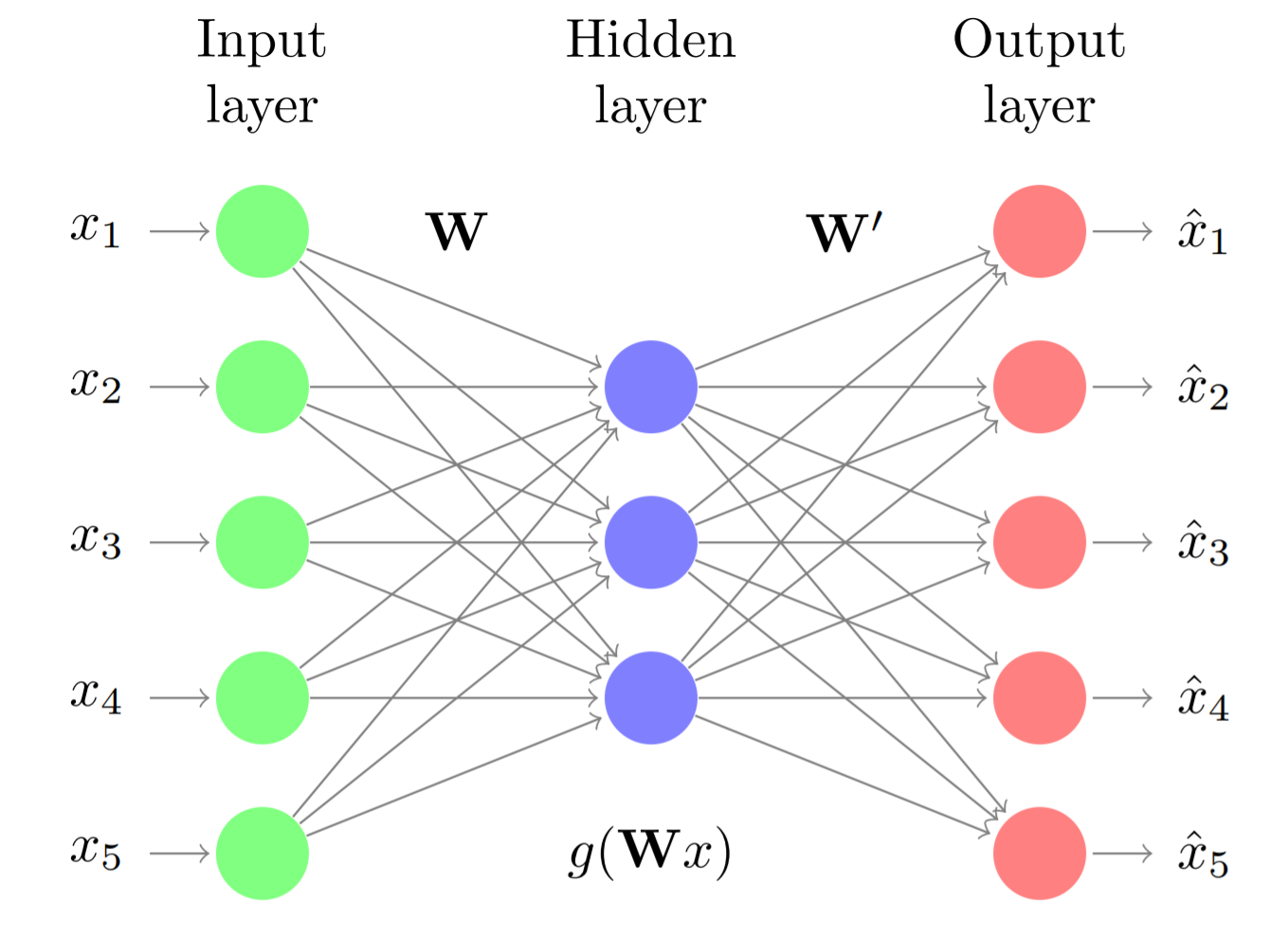
Para conseguir que la salida reconstruida sea lo más parecida posible a la entrada, el modelo debe aprender a capturar toda la información posible en la zona intermedia. Una vez entrenado, la salida de la capa central del autoencoder (la capa con menos neuronas) es una representación de los datos de entrada pero con una dimensionalidad igual el número de neuronas de esta capa.
La principal ventaja de los autoencoders es que no tienen ninguna restricción en cuanto al tipo de relaciones que pueden aprender, por lo tanto, a diferencia del PCA, la reducción de dimensionalidad puede incluir relaciones no lineales. La desventaja es su alto riesgo de sobreentrenamiento (overfitting), por lo que se recomienda emplear pocas épocas y siempre evaluar la evolución del error con un conjunto de validación.
En el caso de utilizar funciones de activación lineales, las variables generadas en el cuello de botella (la capa con menos neuronas), son muy similares a las componentes principales de un PCA pero sin que necesariamente tengan que ser ortogonales entre ellas.
Librerías¶
Una de las implementaciones de autoencoders disponible en python se encuentra en la librería H2O. Esta librería permite generar, entre otros modelos de machine learning, redes neuronales con arquitectura de autoencoder y extraer de forma sencilla los errores de reconstrucción.
# Instalación
# ==============================================================================
#!pip install requests
#!pip install tabulate
#!pip install "colorama>=0.3.8"
#!pip install future
#!pip uninstall h2o
#!pip install -f http://h2o-release.s3.amazonaws.com/h2o/latest_stable_Py.html h2o
# Tratamiento de datos
# ==============================================================================
import numpy as np
import pandas as pd
from mat4py import loadmat
# Gráficos
# ==============================================================================
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
plt.rcParams['lines.linewidth'] = 1.5
plt.rcParams['font.size'] = 8
import seaborn as sns
# Preprocesado y modelado
# ==============================================================================
import h2o
from h2o.estimators.deeplearning import H2OAutoEncoderEstimator
# Configuración warnings
# ==============================================================================
import warnings
warnings.filterwarnings('once')
Datos¶
Los datos empleados se han obtenido de Outlier Detection DataSets (ODDS), un repositorio con datos comúnmente empleados para comparar la capacidad que tienen diferentes algoritmos a la hora de identificar anomalías (outliers). Shebuti Rayana (2016). ODDS Library. Stony Brook, NY: Stony Brook University, Department of Computer Science.
Todos estos conjuntos de datos están etiquetados, se conoce si las observaciones son o no anomalías (variable y). Aunque los métodos que se describen en el documento son no supervisados, es decir, no hacen uso de la variable respuesta, conocer la verdadera clasificación permite evaluar su capacidad para identificar correctamente las anomalías.
- Cardiotocography dataset link:
- Número de observaciones: 1831
- Número de variables: 21
- Número de outliers: 176 (9.6%)
- y: 1 = outliers, 0 = inliers
- Observaciones: todas las variables están centradas y escaladas (media 0, sd 1).
- Referencia: C. C. Aggarwal and S. Sathe, “Theoretical foundations and algorithms for outlier ensembles.” ACM SIGKDD Explorations Newsletter, vol. 17, no. 1, pp. 24–47, 2015. Saket Sathe and Charu C. Aggarwal. LODES: Local Density meets Spectral Outlier Detection. SIAM Conference on Data Mining, 2016.
Los datos están disponibles en formato MATLAB (.mat). Para leer su contenido se emplea la función loadmat() del paquete mat4py.
# Lectura de datos
# ==============================================================================
cardio = loadmat(filename='cardio.mat')
X = pd.DataFrame(cardio['X'])
X.columns = ["col_" + str(i) for i in X.columns]
y = pd.Series(np.array(cardio['y']).flatten(), name='y')
# Creación de un cluster local H2O
# ==============================================================================
h2o.init(
ip = "localhost",
# -1 indica que se empleen todos los cores disponibles.
nthreads = 1,
# Máxima memoria disponible para el cluster.
max_mem_size = "4g",
verbose = False
)
# Se eliminan los datos del cluster por si ya había sido iniciado.
# ==============================================================================
h2o.remove_all()
h2o.no_progress()
# Se transfieren los datos al cluster de h2o
# ==============================================================================
X = h2o.H2OFrame(python_obj= X)
# División de las observaciones en conjunto de entrenamiento y test
# ==============================================================================
X_train, X_test = X.split_frame(
ratios=[0.8],
destination_frames= ["datos_train_H2O", "datos_test_H2O"],
seed = 123
)
Modelo autoencoder¶
# Entrenamiento del modelo autoencoder
# ==============================================================================
# Hiperparámetros:
# - hidden=[10, 3, 10]: arquitectura simétrica con cuello de botella de 3 dimensiones
# - l1 y l2: regularización para prevenir overfitting
# - activation="Tanh": permite capturar relaciones no lineales
autoencoder = H2OAutoEncoderEstimator(
activation = "Tanh",
standardize = True,
l1 = 0.01,
l2 = 0.01,
hidden = [10, 3, 10],
epochs = 100,
ignore_const_cols = False,
score_each_iteration = True,
seed = 12345
)
autoencoder.train(
x = X.columns,
training_frame = X_train,
validation_frame = X_test,
max_runtime_secs = None,
ignored_columns = None,
verbose = False
)
autoencoder.summary()
| layer | units | type | dropout | l1 | l2 | mean_rate | rate_rms | momentum | mean_weight | weight_rms | mean_bias | bias_rms | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 21 | Input | 0.0 | ||||||||||
| 2 | 10 | Tanh | 0.0 | 0.01 | 0.01 | 0.0596206 | 0.0131358 | 0.0 | -0.0006532 | 0.0538940 | 0.0038406 | 0.0113920 | |
| 3 | 3 | Tanh | 0.0 | 0.01 | 0.01 | 0.0617362 | 0.0088655 | 0.0 | -0.0384981 | 0.2068415 | -0.0096374 | 0.0139275 | |
| 4 | 10 | Tanh | 0.0 | 0.01 | 0.01 | 0.0607378 | 0.0105192 | 0.0 | 0.0415092 | 0.2210941 | -0.0016290 | 0.0054258 | |
| 5 | 21 | Tanh | 0.01 | 0.01 | 0.0562047 | 0.0162091 | 0.0 | 0.0018195 | 0.0738565 | 0.0240189 | 0.0567052 |
Diagnostico¶
Para identificar el número de épocas adecuado se emplea la evolución del error de entrenamiento y validación.
fig, ax = plt.subplots(1, 1, figsize=(6, 3))
autoencoder.scoring_history().plot(x='epochs', y='training_rmse', ax=ax)
autoencoder.scoring_history().plot(x='epochs', y='validation_rmse', ax=ax)
ax.set_title('Evolución del error de entrenamiento y validación');
A partir de las 15 épocas, la reducción en el rmse es mínima. Una vez identificado el número óptimo de épocas, se reentrena el modelo, esta vez con todos los datos.
# Entrenamiento del modelo final
# ==============================================================================
autoencoder = H2OAutoEncoderEstimator(
activation = "Tanh",
standardize = True,
l1 = 0.01,
l2 = 0.01,
hidden = [10, 3, 10],
epochs = 15,
ignore_const_cols = False,
score_each_iteration = True,
seed = 12345
)
autoencoder.train(
x = X.columns,
training_frame = X,
verbose = False
)
autoencoder
Error de reconstrucción¶
El método anomaly() de un modelo H2OAutoEncoderEstimator permite obtener el error de reconstrucción. Para ello, realiza automáticamente la codificación, decodificación y la comparación de los valores reconstruidos con los valores originales.
El error cuadrático medio de reconstrucción de una observación se calcula como el promedio de las diferencias al cuadrado entre el valor original de sus variables y el valor reconstruido, es decir, el promedio de los errores de reconstrucción de todas sus variables elevados al cuadrado.
# Cálculo error de reconstrucción
# ==============================================================================
error_reconstruccion = autoencoder.anomaly(test_data = X)
error_reconstruccion = error_reconstruccion.as_data_frame()
error_reconstruccion = error_reconstruccion['Reconstruction.MSE']
Detección de anomalías¶
Una vez que el error de reconstrucción ha sido calculado, se puede emplear como criterio para identificar anomalías. Asumiendo que la reducción de dimensionalidad se ha realizado de forma que la mayoría de los datos (los normales) queden bien representados, aquellas observaciones con mayor error de reconstrucción deberían ser las más atípicas.
En la práctica, si se está empleando esta estrategia de detección es porque no se dispone de datos etiquetados, es decir, no se conoce qué observaciones son realmente anomalías. Sin embargo, como en este ejemplo se dispone de la clasificación real, se puede verificar si realmente los datos anómalos tienen errores de reconstrucción más elevados.
# Distribución del error de reconstrucción en anomalías y no anomalías
# ==============================================================================
resultados = pd.DataFrame({
'error_reconstruccion': error_reconstruccion,
'anomalia': y.astype(str)
})
fig, ax = plt.subplots(figsize=(5, 3))
sns.boxplot(
x = 'error_reconstruccion',
y = 'anomalia',
hue = 'anomalia',
data = resultados,
ax = ax
)
ax.set_xscale("log")
ax.set_title('Distribución de los errores de reconstrucción')
ax.set_xlabel('log(Error de reconstrucción)')
ax.set_ylabel('clasificación (0 = normal, 1 = anomalía)');
La distribución de los errores de reconstrucción en el grupo de las anomalías (1) es claramente superior. Sin embargo, al existir solapamiento, si se clasifican las n observaciones con mayor error de reconstrucción como anomalías, se incurriría en errores de falsos positivos.
Acorde a la documentación, el set de datos Cardiotocogrpahy contiene 176 anomalías. Véase la matriz de confusión resultante si se clasifican como anomalías las 176 observaciones con mayor error de reconstrucción.
# Matriz de confusión de la clasificación final
# ==============================================================================
resultados = (
resultados
.sort_values('error_reconstruccion', ascending=False)
.reset_index(drop=True)
)
resultados['clasificacion'] = np.where(resultados.index <= 176, 1, 0)
pd.crosstab(
resultados['anomalia'],
resultados['clasificacion'],
rownames=['valor real'],
colnames=['prediccion']
)
| prediccion | 0 | 1 |
|---|---|---|
| valor real | ||
| 0.0 | 1608 | 47 |
| 1.0 | 46 | 130 |
De las 177 observaciones identificadas como anomalías, el 73% (130/177) lo son. El modelo consigue identificar un porcentaje elevado de las anomalías, aun así, tiene dificultad para separar completamente las anomalías de las observaciones normales.
Reentrenamiento iterativo¶
El modelo de autoencoder anterior se ha entrenado empleando todas las observaciones, incluyendo las potenciales anomalías. Dado que el objetivo es generar un espacio de proyección para datos “normales”, se puede mejorar el resultado reentrenando el modelo pero esta vez excluyendo las $n$ observaciones con mayor error de reconstrucción (potenciales anomalías).
Se repite la detección de anomalías pero, esta vez, descartando las observaciones con un error de reconstrucción superior al cuantil 0.8. Con este umbral se eliminan aproximadamente el 20% de observaciones más atípicas, permitiendo que el modelo se concentre en aprender la estructura de los datos normales.
# Eliminación observaciones con error de reconstrucción superior al cuantil 0.8
# ==============================================================================
cuantil = np.quantile(a=error_reconstruccion, q=0.8)
X_pandas = X.as_data_frame()
X_trimmed = X_pandas.loc[error_reconstruccion < cuantil, :]
X_trimmed = h2o.H2OFrame(python_obj=X_trimmed)
# Reentrenamiento del modelo con datos filtrados
# ==============================================================================
# Se reentrena el modelo utilizando solo las observaciones con menor error de reconstrucción
autoencoder.train(
x = X_trimmed.columns,
training_frame = X_trimmed,
verbose = False
)
Model Details ============= H2OAutoEncoderEstimator : Deep Learning Model Key: DeepLearning_model_python_1769118893743_6
| layer | units | type | dropout | l1 | l2 | mean_rate | rate_rms | momentum | mean_weight | weight_rms | mean_bias | bias_rms | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 21 | Input | 0.0 | ||||||||||
| 2 | 10 | Tanh | 0.0 | 0.01 | 0.01 | 0.0291871 | 0.0219678 | 0.0 | -0.0055397 | 0.0933082 | -0.0022585 | 0.0170172 | |
| 3 | 3 | Tanh | 0.0 | 0.01 | 0.01 | 0.0169608 | 0.0053685 | 0.0 | -0.0130222 | 0.2824453 | -0.0043661 | 0.0221675 | |
| 4 | 10 | Tanh | 0.0 | 0.01 | 0.01 | 0.0167799 | 0.0084733 | 0.0 | -0.0478559 | 0.2907931 | -0.0030111 | 0.0088228 | |
| 5 | 21 | Tanh | 0.01 | 0.01 | 0.0178878 | 0.0104283 | 0.0 | -0.0072167 | 0.0989479 | 0.0150805 | 0.0496585 |
ModelMetricsAutoEncoder: deeplearning ** Reported on train data. ** MSE: 0.023428990459610305 RMSE: 0.15306531435831666
| timestamp | duration | training_speed | epochs | iterations | samples | training_rmse | training_mse | |
|---|---|---|---|---|---|---|---|---|
| 2026-01-22 23:02:07 | 0.045 sec | 0.00000 obs/sec | 0.0 | 0 | 0.0 | 0.2251519 | 0.0506934 | |
| 2026-01-22 23:02:07 | 0.151 sec | 22226 obs/sec | 1.4726776 | 1 | 2156.0 | 0.1530653 | 0.0234290 | |
| 2026-01-22 23:02:07 | 0.240 sec | 24762 obs/sec | 2.9938525 | 2 | 4383.0 | 0.1596385 | 0.0254845 | |
| 2026-01-22 23:02:07 | 0.328 sec | 25616 obs/sec | 4.5143443 | 3 | 6609.0 | 0.1597282 | 0.0255131 | |
| 2026-01-22 23:02:07 | 0.411 sec | 26154 obs/sec | 6.0027322 | 4 | 8788.0 | 0.1590834 | 0.0253075 | |
| 2026-01-22 23:02:07 | 0.498 sec | 26326 obs/sec | 7.4986339 | 5 | 10978.0 | 0.1581181 | 0.0250013 | |
| 2026-01-22 23:02:07 | 0.577 sec | 26936 obs/sec | 8.9972678 | 6 | 13172.0 | 0.1596812 | 0.0254981 | |
| 2026-01-22 23:02:07 | 0.660 sec | 27264 obs/sec | 10.5034153 | 7 | 15377.0 | 0.1597646 | 0.0255247 | |
| 2026-01-22 23:02:07 | 0.741 sec | 27523 obs/sec | 11.9945355 | 8 | 17560.0 | 0.1597635 | 0.0255244 | |
| 2026-01-22 23:02:07 | 0.822 sec | 27762 obs/sec | 13.5020492 | 9 | 19767.0 | 0.1632883 | 0.0266631 | |
| 2026-01-22 23:02:07 | 0.902 sec | 27987 obs/sec | 15.0259563 | 10 | 21998.0 | 0.1580599 | 0.0249829 | |
| 2026-01-22 23:02:07 | 0.910 sec | 27880 obs/sec | 15.0259563 | 10 | 21998.0 | 0.1530653 | 0.0234290 |
| variable | relative_importance | scaled_importance | percentage |
|---|---|---|---|
| col_12 | 1.0 | 1.0 | 0.1526174 |
| col_20 | 0.9821752 | 0.9821752 | 0.1498970 |
| col_0 | 0.7182886 | 0.7182886 | 0.1096233 |
| col_11 | 0.6908948 | 0.6908948 | 0.1054426 |
| col_18 | 0.6157004 | 0.6157004 | 0.0939666 |
| col_4 | 0.5618078 | 0.5618078 | 0.0857417 |
| col_14 | 0.3628029 | 0.3628029 | 0.0553700 |
| col_7 | 0.2872897 | 0.2872897 | 0.0438454 |
| col_16 | 0.2419246 | 0.2419246 | 0.0369219 |
| col_3 | 0.2130911 | 0.2130911 | 0.0325214 |
| --- | --- | --- | --- |
| col_9 | 0.1780681 | 0.1780681 | 0.0271763 |
| col_17 | 0.1570718 | 0.1570718 | 0.0239719 |
| col_19 | 0.1522639 | 0.1522639 | 0.0232381 |
| col_8 | 0.0910602 | 0.0910602 | 0.0138974 |
| col_13 | 0.0448850 | 0.0448850 | 0.0068502 |
| col_10 | 0.0342585 | 0.0342585 | 0.0052284 |
| col_5 | 0.0049315 | 0.0049315 | 0.0007526 |
| col_15 | 0.0036547 | 0.0036547 | 0.0005578 |
| col_2 | 0.0031253 | 0.0031253 | 0.0004770 |
| col_6 | 0.0013269 | 0.0013269 | 0.0002025 |
[21 rows x 4 columns]
[tips] Use `model.explain()` to inspect the model. -- Use `h2o.display.toggle_user_tips()` to switch on/off this section.
# Error de recostrucción
# ==============================================================================
error_reconstruccion = autoencoder.anomaly(test_data = X)
error_reconstruccion = error_reconstruccion.as_data_frame()
error_reconstruccion = error_reconstruccion['Reconstruction.MSE']
# Matriz de confusión de la clasificación tras reentrenamiento
# ==============================================================================
resultados = pd.DataFrame({
'error_reconstruccion' : error_reconstruccion,
'anomalia' : y.astype(str)
})
resultados = (
resultados
.sort_values('error_reconstruccion', ascending=False)
.reset_index(drop=True)
)
resultados['clasificacion'] = np.where(resultados.index <= 176, 1, 0)
pd.crosstab(
resultados['anomalia'],
resultados['clasificacion'],
rownames=['valor real'],
colnames=['prediccion']
)
| prediccion | 0 | 1 |
|---|---|---|
| valor real | ||
| 0.0 | 1617 | 38 |
| 1.0 | 37 | 139 |
Tras descartar el 20% de las observaciones con mayor error y reentrenar el autoencoder, se observa una mejora en la capacidad del modelo para identificar anomalías. El reentrenamiento iterativo permite que el modelo se especialice en aprender la estructura de los datos normales, aumentando así la separación entre los errores de reconstrucción de observaciones normales y anómalas.
✏️ Note
En escenarios reales sin etiquetas, el número de anomalías a identificar debe determinarse mediante métodos como el análisis de la distribución de errores, pruebas de dominio o percentiles específicos basados en el conocimiento del negocio.
PyOD¶
La librería PyOD es una biblioteca de Python especializada en la detección de anomalías. Proporciona una amplia gama de algoritmos, tanto clásicos como basados en aprendizaje profundo, incluyendo autoencoders.
A continuación, se muestra un ejemplo de cómo utilizar PyOD para detectar anomalías con autoencoders en el conjunto de datos Cardiotocography.
Librarías¶
# Librerías
# ==============================================================================
from pyod.models.auto_encoder import AutoEncoder
Datos¶
# Lectura de datos
# ==============================================================================
cardio = loadmat(filename='cardio.mat')
X = pd.DataFrame(cardio['X'])
X.columns = ["col_" + str(i) for i in X.columns]
y = pd.Series(np.array(cardio['y']).flatten(), name='y')
Modelo auntoencoder¶
# Autoencoder con PyOD
# ==============================================================================
autoencoder_pyod = AutoEncoder(
hidden_neuron_list = [10, 3, 10],
epoch_num = 50,
contamination = 0.1,
preprocessing = True,
hidden_activation_name = 'relu',
batch_norm = True,
dropout_rate = 0.2,
lr = 0.005,
batch_size = 32,
optimizer_name = 'adam',
random_state = 12345
)
autoencoder_pyod.fit(X=X)
Detección de anomalías¶
Los modelos de PyOD tienen dos métodos de predicción con los que se obtiene distinta información. Con el método predict() se devuelve directamente la clasificación de anomalía (-1) o no anomalía (1) acorde a la proporción de contaminación que se ha indicado en la definición del modelo.
Con el método decision_function() se obtiene un puntaje de anomalía para cada observación, donde valores más altos indican una mayor probabilidad de ser una anomalía. Este puntaje puede utilizarse para establecer umbrales personalizados o para comparar la "anomalidad" relativa entre observaciones.
# Detección de anomalías: scores de anomalía
# ==============================================================================
score_anomalia = autoencoder_pyod.decision_function(X=X)
score_anomalia
array([2.9682167, 3.2247372, 4.0680285, ..., 4.420389 , 4.218177 ,
6.6297894], shape=(1831,), dtype=float32)
# Detección de anomalías: clasificación binaria
# ==============================================================================
clasificacion_anomalia = autoencoder_pyod.predict(X=X)
clasificacion_anomalia
array([0, 0, 0, ..., 0, 0, 1], shape=(1831,))
# Matriz de confusión de la clasificación final
# ==============================================================================
df_resultados = pd.DataFrame({
'score' : score_anomalia,
'anomalia' : y.astype(str)
})
df_resultados = (
df_resultados
.sort_values('score', ascending=False)
.reset_index(drop=True)
)
df_resultados['clasificacion'] = np.where(df_resultados.index <= 176, 1, 0)
pd.crosstab(
df_resultados['anomalia'],
df_resultados['clasificacion'],
rownames=['valor real'],
colnames=['prediccion']
)
| prediccion | 0 | 1 |
|---|---|---|
| valor real | ||
| 0.0 | 1556 | 99 |
| 1.0 | 98 | 78 |
En este conjunto de datos, el autoencoder de PyOD consigue peores resultados que el de H20.
Información de sesión¶
import session_info
session_info.show(html=False)
----- h2o 3.46.0.9 mat4py 0.6.0 matplotlib 3.10.8 numpy 2.2.6 pandas 2.3.3 pyod 2.0.6 seaborn 0.13.2 session_info v1.0.1 ----- IPython 9.8.0 jupyter_client 8.7.0 jupyter_core 5.9.1 ----- Python 3.13.11 | packaged by Anaconda, Inc. | (main, Dec 10 2025, 21:28:48) [GCC 14.3.0] Linux-6.14.0-37-generic-x86_64-with-glibc2.39 ----- Session information updated at 2026-01-22 23:11
Bibliografía¶
Outlier Analysis Aggarwal, Charu C.
Outlier Ensembles: An Introduction by Charu C. Aggarwal, Saket Sathe
Introduction to Machine Learning with Python: A Guide for Data Scientists
Python Data Science Handbook by Jake VanderPlas
Instrucciones para citar¶
¿Cómo citar este documento?
Si utilizas este documento o alguna parte de él, te agradecemos que lo cites. ¡Muchas gracias!
Detección de anomalías con autoencoders y python por Joaquín Amat Rodrigo, disponible bajo una licencia Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0 DEED) en https://www.cienciadedatos.net/documentos/py32-deteccion-anomalias-autoencoder-python.html
¿Te ha gustado el artículo? Tu ayuda es importante
Tu contribución me ayudará a seguir generando contenido divulgativo gratuito. ¡Muchísimas gracias! 😊
Este documento creado por Joaquín Amat Rodrigo tiene licencia Attribution-NonCommercial-ShareAlike 4.0 International.
Se permite:
-
Compartir: copiar y redistribuir el material en cualquier medio o formato.
-
Adaptar: remezclar, transformar y crear a partir del material.
Bajo los siguientes términos:
-
Atribución: Debes otorgar el crédito adecuado, proporcionar un enlace a la licencia e indicar si se realizaron cambios. Puedes hacerlo de cualquier manera razonable, pero no de una forma que sugiera que el licenciante te respalda o respalda tu uso.
-
No-Comercial: No puedes utilizar el material para fines comerciales.
-
Compartir-Igual: Si remezclas, transformas o creas a partir del material, debes distribuir tus contribuciones bajo la misma licencia que el original.

