更多机器学习内容:Python 机器学习

简介¶
线性回归是一种统计方法,旨在通过拟合线性方程来建模连续变量与一个或多个自变量之间的关系。当只有一个自变量时,称为简单线性回归;当有多个自变量时,称为多元线性回归。根据上下文,被建模的变量称为因变量或响应变量,而自变量则称为回归变量、预测变量或特征。
本文档逐步介绍了线性回归的理论基础、关键的实践考量,以及如何在 Python 中创建这些模型的示例。
Python 中的线性回归模型
Python 中最常用的两种线性回归模型实现是:scikit-learn 和 statsmodels。虽然两者都经过高度优化,但 Scikit-learn 主要专注于预测,这意味着它缺乏显示许多推断所需模型特征的功能。而 Statsmodels 在这方面则更加全面。
数学定义¶
线性回归模型(Legendre、Gauss、Galton 和 Pearson)假设,给定一组观测值
$\{y_i, x_{i1},...,x_{ip}\}^{n}_{i=1}$,响应变量 $y$ 的均值 $\mu$ 与回归变量 $x_1, ..., x_p$ 线性相关,其方程为:
该方程的结果称为总体回归线,它描述了预测变量与响应变量均值之间的关系。
统计文献中另一个常见的定义是:
$$ y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + ... + \beta_p x_{ip} + \epsilon_i $$在这种情况下,方程指的是特定观测值 $i$ 的 $y$ 值。由于单个观测值永远不会完全等于均值,因此需要包含一个误差项 $\epsilon$。
在两种情况下,模型各成分的解释是相同的:
$\beta_0$:截距,表示当所有预测变量为零时,响应变量 $y$ 的平均值。
$\beta_j$:偏回归系数,表示当预测变量 $x_j$ 增加一个单位时,在其他变量保持不变的情况下,对 $y$ 的平均影响。
$\epsilon$:残差(误差项),表示观测值与 $y$ 估计值之间的差异。它捕获了所有影响 $y$ 但未包含在模型中的因素的影响。
在大多数情况下,总体值 $\beta_0$ 和 $\beta_j$ 是未知的。因此,需要从样本中获取它们的估计值 $\hat{\beta}_0$ 和 $\hat{\beta}_j$。拟合模型就是从可用数据中估计回归系数,使得似然性最大化,即找到最可能生成观测数据的模型。
最常用的估计方法是普通最小二乘法(OLS),它通过最小化每个训练数据点与回归线之间垂直偏差的平方和,来找到最佳拟合线(或在多元回归情况下的平面)。
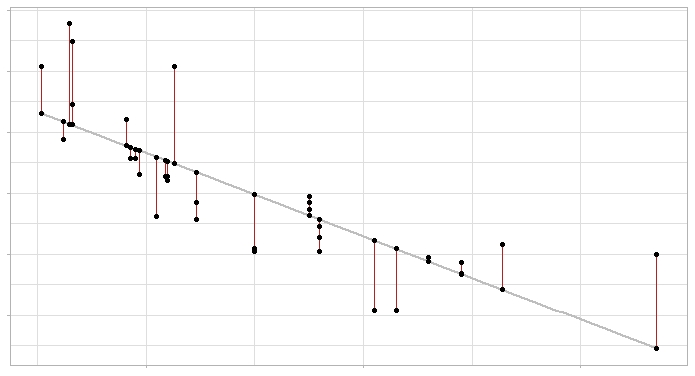
线性回归模型及其误差:灰色线表示回归线(模型),红色线段表示回归线与每个观测值之间的误差。
在计算上,使用矩阵形式进行这些计算更为高效:
$$ \mathbf{y} = \mathbf{X}^T \mathbf{\beta} + \epsilon $$一旦估计出系数,每个观测值的估计值($\hat{y}_i$)可以通过以下公式获得:
$$ \hat{y}_i = \hat{\beta}_0 + \hat{\beta}_1 x_{i1} + \hat{\beta}_2 x_{i2} + \dots + \hat{\beta}_p x_{ip} $$最后,模型方差($\hat{\sigma}^2$)的估计值通过以下公式获得:
$$ \hat{\sigma}^2 = \frac{\sum^n_{i=1} \hat{\epsilon}_i^2}{n-p} = \frac{\sum^n_{i=1} (y_i - \hat{y}_i)^2}{n-p} $$其中 $n$ 是观测值的数量,$p$ 是预测变量的数量。
模型解释¶
线性回归模型中需要解释的主要元素是预测变量系数:
$\beta_{0}$ 是截距,对应于当所有预测变量为零时响应变量 $y$ 的期望值。
$\beta_{j}$,每个预测变量的偏回归系数,表示当预测变量 $x_{j}$ 增加一个单位,同时保持其他变量不变时,响应变量 $y$ 的期望平均变化。
每个偏回归系数的大小取决于相应预测变量的测量单位,因此其大小与每个预测变量的重要性无关。
为了确定每个变量在模型中的影响,使用标准化偏系数。这些系数是通过在拟合模型之前对预测变量进行标准化(减去均值并除以标准差)来获得的。在这种情况下,$\beta_{0}$ 对应于当所有预测变量处于其均值时响应变量的期望值,$\beta_{j}$ 表示当预测变量 $x_{j}$ 增加一个标准差,同时保持其他变量不变时,响应变量的期望平均变化。
虽然回归系数通常是解释线性模型时的主要关注点,但还有许多其他方面需要考虑(整体模型显著性、预测变量显著性、正态性条件等)。当模型的唯一目标是进行预测时,这些方面通常不太受关注。然而,当进行推断时,即解释预测变量与响应变量之间的关系时,这些方面就变得非常重要。本文档将逐一介绍这些方面。
"线性"的含义
回归模型中的"线性"一词指的是参数以线性方式纳入方程,而不一定意味着每个预测变量与响应变量之间的关系必须遵循线性模式。
以下方程展示了一个线性模型,其中预测变量 $x_1$ 与 y 之间不是线性关系:
$$y = \beta_0 + \beta_1x_1 + \beta_2log(x_1) + \epsilon$$import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
plt.rcParams.update({'font.size': 10, 'lines.linewidth': 1.5})
x1 = np.linspace(1,5, num=100)
x2 = np.linspace(1,5, num=100)
y = 0.0 + 0.5*x1 - 0.8*np.log(x2)
fig, ax = plt.subplots(figsize=(5, 2.5))
ax.plot(x1, y)
ax.set_xlabel("x1")
ax.set_ylabel("y");
相比之下,以下方程不代表线性模型:
$$y = \beta_0 + \beta_1x_1^{\beta_2} + \epsilon$$然而,一些非线性关系可以转换为线性形式:
$$y = \beta_0x_1^{\beta_1}\epsilon$$对两边取对数:
$$\log(y) = \log(\beta_0) + \beta_1 \log(x_1) + \log(\epsilon)$$这种转换使模型能够以线性形式表达,从而适用于线性回归技术。
模型拟合优度¶
模型拟合完成后,需要验证其有效性,因为即使它代表了所有可能拟合线中的最佳拟合线,误差仍可能很大。评估拟合质量最常用的指标是残差标准误差(RSE)和决定系数($R^2$)。
残差标准误差(RSE)
残差标准误差(RSE)衡量任何估计点与回归线的平均偏差。它与响应变量具有相同的单位。判断 RSE 是否较高的常用方法是将其除以响应变量的均值,从而获得百分比偏差。
$$RSE = \sqrt{\frac{1}{n-p-1}RSS}$$在简单线性回归模型中,由于只有一个预测变量,$(n-p-1) = (n-2)$。
决定系数($R^2$)
$R^2$ 描述了模型解释的响应变量方差相对于总方差的比例。其值介于 0 和 1 之间。由于它是无量纲的,与 RSE 相比更容易解释。
$$R^{2}=\frac{\text{总平方和 - 残差平方和}}{\text{总平方和}}=$$ $$1-\frac{\text{残差平方和}}{\text{总平方和}} = $$ $$1-\frac{\sum(\hat{y_i}-y_i)^2}{\sum(y_i-\overline{y})^2}$$在简单线性回归模型中,$R^2$ 值对应于 $x$ 和 $y$ 之间皮尔逊相关系数(r)的平方。但在多元回归中并非如此。
在多元线性回归模型中,模型中包含的预测变量越多,$R^2$ 值就越高。这是因为每个预测变量,即使影响很小,也有助于解释 $y$ 观测变异性的一部分。因此,$R^2$ 不能用于比较具有不同预测变量数量的模型。
$R^2_{adjusted}$ 对模型中添加的每个预测变量引入惩罚。惩罚值取决于使用的预测变量数量和样本大小,即自由度。样本越大,模型中可以包含的预测变量就越多。调整后的 $R^2$ 有助于找到最佳模型,即用最少的预测变量最有效地解释 $y$ 变异性的模型。
$$R^{2}_{adj} = 1 - \frac{SSE}{SST} \times \frac{n-1}{n-p-1} = R^{2} - (1-R^{2}) \frac{n-1}{n-p-1} = 1 - \frac{SSE/df_{e}}{SST/df_{t}}$$其中 $SSE$ 是模型解释的变异性(解释平方和),$SST$ 是 $y$ 的总变异性(总平方和),$n$ 是样本大小,$p$ 是模型中包含的预测变量数量。
模型显著性 F 检验¶
拟合线性模型时首先要评估的结果之一是 $F$ 检验的结果。该检验回答的问题是:模型整体是否能比随机预期更好地预测响应变量,或者等效地,模型中是否至少有一个预测变量具有显著贡献。为了进行此检验,将目标模型的残差平方和与不含预测变量的模型(仅由均值组成,也称为总平方和 $TSS$)的残差平方和进行比较。
$$F = \frac{(TSS - RSS)/(p-1)}{RSS/(n-p)}$$通常,该检验的原假设和备择假设描述为:
- $H_0$: $\beta_1$ = ... = $\beta_{p-1} = 0$
- $H_a$: 至少有一个 $\beta_i \neq 0$
如果 $F$ 检验显著,则意味着模型是有用的,但不一定意味着它是最佳模型。可能存在一个不必要的预测变量。
预测变量的显著性¶
在大多数情况下,尽管回归分析应用于样本,但最终目标是获得一个能够解释整个总体中变量之间关系的线性模型。这意味着生成的模型是基于样本中观测到的关系对总体关系的估计,因此会受到变化的影响。对于线性回归方程中的每个系数($\beta_j$),可以计算其显著性(p 值)和置信区间。最常用的统计检验是 $T$ 检验,不过也有非参数替代方法。
线性模型中系数($\beta_j$)的显著性检验考虑以下假设:
$H_0$:预测变量 $x_j$ 对模型没有贡献($\beta_j = 0$),在其他预测变量存在的情况下。在简单线性回归中,这也可以解释为两个变量之间没有线性关系,即模型的斜率为零 $\beta_j = 0$。
$H_a$:预测变量 $x_j$ 对模型有贡献($\beta_j \neq 0$),在其他预测变量存在的情况下。在简单线性回归中,这也可以解释为两个变量之间存在线性关系,即模型的斜率不为零 $\beta_j \neq 0$。
T 统计量和 p 值的计算:
其中
$$SE(\hat{\beta}_j)^2 = \frac{\sigma^2}{\sum^n_{i=1}(x_{ji} -\overline{x})^2}$$误差方差 $\sigma^2$ 通过残差标准误差(RSE)来估计,RSE 可以理解为响应变量与真实回归线之间的平均差异。在简单线性回归中,RSE 等于:
$$RSE = \sqrt{\frac{1}{n-2}RSS} = \sqrt{\frac{1}{n-2}\sum^n_{i=1}(y_i -\hat{y}_i)}$$自由度(df)= 观测数 - 2 = 观测数 - 预测变量数 - 1
p 值 = P(|t| > 计算的 t 值)
置信区间
观测数 $n$ 越少,计算模型标准误差的能力就越弱。因此,估计的回归系数的准确性会降低。这在多元回归中尤为重要。
在使用 statsmodels 生成的模型中,除了回归系数值外,还会返回每个系数的 t 统计量值,以及相应的 p 值和置信区间。这不仅可以了解估计值,还可以知道它们是否显著不同于 0,即它们是否对模型有贡献。
为使上述计算有效,必须假设残差是独立的,并且服从均值为 0、方差为 $\sigma^2$ 的正态分布。当不满足正态性条件时,可以使用置换检验来计算显著性(p 值),使用自助法来计算置信区间。
分类变量作为预测变量¶
当引入分类变量作为预测变量时,通常以一个水平作为参考水平(通常编码为 0),其他水平与之进行比较。如果分类预测变量有两个以上的水平,则生成所谓的虚拟变量或独热编码。这些是为分类预测变量的每个水平创建的变量,可以取值 0 或 1。每次使用模型进行预测时,每个预测变量只有一个虚拟变量取值为 1(对应于该预测变量在该情况下所取的水平),其余为 0。每个虚拟变量的偏回归系数 $\beta_j$ 表示该水平相对于该预测变量的参考水平对因变量 $y$ 的平均百分比影响。
通过一个例子可以更好地理解虚拟变量的概念。假设一个模型中,响应变量体重根据身高和受试者的国籍进行预测。国籍变量是定性的,有 3 个水平(美国人、欧洲人和亚洲人)。尽管初始预测变量是国籍,但为每个水平创建一个新变量,该变量可以是 0 或 1。因此,完整模型的方程为:
$$体重 = \beta_0 + \beta_1身高 + \beta_2美国人 + \beta_3欧洲人 + \beta_4亚洲人$$如果受试者是欧洲人,则美国人和亚洲人的虚拟变量被视为 0,因此该情况下的模型为:
$$体重 = \beta_0 + \beta_1身高 + \beta_3欧洲人$$预测¶
一旦生成了有效的模型,就可以为预测变量 $x$ 的新值预测响应变量 $y$ 的值。需要注意的是,预测原则上应限制在用于训练模型的观测值范围内。这很重要,因为虽然线性模型可以外推,但只有在该范围内,我们才能确信满足模型有效的条件。使用回归生成的方程来计算预测:
$$\hat{y}_i= \hat{\beta}_0 + \hat{\beta}_1 x_{i1} + \hat{\beta}_2 x_{i2} + ... + \hat{\beta}_p x_{ip}$$由于模型是从样本中获得的,回归系数的估计值具有相关误差,由此生成的预测值也是如此。衡量预测相关不确定性有两种方法:
- 置信区间: 对于给定的 $x$ 值,响应变量 $y$ 平均期望值的区间。
- 预测区间: 对于给定的 $x$ 值,响应变量 $y$ 期望值的区间。
虽然两者看起来相似,但区别在于置信区间适用于给定 $x$ 值的 $y$ 的平均期望值,而预测区间则不适用于平均值。因此,后者总是比前者更宽。
置信区间和预测区间误差边界计算方式的一个特点是,随着 $x$ 值接近观测范围的极端值,区间会变宽。
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
bateos = [5659, 5710, 5563, 5672, 5532, 5600, 5518, 5447, 5544, 5598,
5585, 5436, 5549, 5612, 5513, 5579, 5502, 5509, 5421, 5559,
5487, 5508, 5421, 5452, 5436, 5528, 5441, 5486, 5417, 5421]
runs = [855, 875, 787, 730, 762, 718, 867, 721, 735, 615, 708, 644, 654, 735,
667, 713, 654, 704, 731, 743, 619, 625, 610, 645, 707, 641, 624, 570,
593, 556]
data = pd.DataFrame({'hits': bateos, 'runs': runs})
fig, ax = plt.subplots(figsize=(5, 2.5))
sns.regplot(x='runs', y='hits', data=data, ax = ax);
为什么会这样?观察置信区间标准误差的公式,分子包含项 $(x_k - \bar{x})^2$(预测区间也是如此)。
$$\sqrt{MSE \left(\frac{1}{n} + \frac{(x_k - \bar{x})^2}{\sum^n_{i=1}(x_i - \bar{x}^2)} \right)}$$该项对应于进行预测的值 $x_k$ 与预测变量 $x$ 观测值均值 $\bar{x}$ 之间差值的平方。$x_k$ 距离 $\bar{x}$ 越远,分子越大,因此标准误差越大。这就是为什么当 $x$ 值远离观测值均值时,区间会变宽的原因。
模型验证¶
一旦选择了可用数据能创建的最佳模型,就必须验证其预测未用于训练的新观测值的能力。这样可以检验模型是否能够泛化。常用的策略是将数据随机分成两组,用第一组拟合模型,用第二组估计预测准确性。
分区的适当大小在很大程度上取决于可用数据的数量和误差估计所需的置信水平。80%-20% 的分割通常能产生良好的结果。
更稳健的策略是使用交叉验证,即将数据分成 $k$ 组(折叠),使用 $k-1$ 组训练模型,剩余一组用于估计预测误差。这个过程重复 $k$ 次,每次使用不同的折叠作为测试集。最终误差是每次迭代中获得的误差的平均值。
线性回归的条件¶
为使基于最小二乘法的线性回归模型及其得出的结论完全有效,必须验证其数学推导所依据的假设。在实践中,很少能满足所有假设或证明满足所有假设。然而,这并不意味着模型没有用处。重要的是要意识到这些假设及其对模型结论可能产生的影响。
无共线性或多重共线性:
在多元线性模型中,预测变量必须是独立的;它们之间不应存在共线性。当一个预测变量与模型中的一个或多个其他预测变量线性相关时,就会发生共线性。共线性的结果是无法准确识别每个预测变量对响应变量的个别影响,这导致估计的回归系数方差增加,甚至无法确定其统计显著性。此外,数据的微小变化会导致系数估计值的巨大变化。虽然真正的共线性只有在预测变量之间的简单或多重相关系数为 1 时才存在(这在现实中很少发生),但通常会遇到所谓的近似共线性或不完全多重共线性。
没有特定的统计方法来确定回归模型预测变量之间是否存在共线性或多重共线性。然而,已经制定了许多实用规则来评估对模型的影响。建议的步骤是:
如果决定系数 $R^2$ 很高,但没有一个预测变量显著,则有共线性的迹象。
创建一个相关矩阵,计算每对预测变量之间的线性关系。需要注意的是,即使没有获得高相关系数,也不能排除多重共线性。三个或更多变量之间可能存在几乎完美的线性关系,而这些变量成对之间的简单相关性可能不超过 0.5。
为每个预测变量相对于其他预测变量生成一个简单线性回归模型。如果这些模型中有任何一个具有较高的决定系数 $R^2$,则可能表明存在潜在的共线性。
容忍度(TOL)和方差膨胀因子(VIF)。这两个参数本质上量化相同的事物(一个是另一个的倒数)。每个预测变量的 VIF 使用以下公式计算:
其中 $R^2$ 是通过预测变量 $X_j$ 对其他预测变量的回归获得的。这是最推荐的方法,常用的参考限值为:
VIF = 1:完全没有共线性。
1 < VIF < 5:回归可能受到一定程度的共线性影响。
5 < VIF < 10:回归可能受到较大的共线性影响。
容忍度项是 $\frac{1}{VIF}$,因此推荐的限值在 1 和 0.1 之间。
如果发现预测变量之间存在共线性,有两种可能的解决方案。第一种是排除其中一个问题预测变量,同时尝试保留研究者认为真正影响响应变量的那个。这种措施通常对模型的预测能力影响不大,因为在存在共线性的情况下,一个预测变量提供的信息在另一个预测变量存在时是多余的。第二种选择是将共线变量合并为一个预测变量,尽管这有失去其解释性的风险。
当试图建立因果关系时,共线性可能导致非常错误的结论,使得某个变量看起来是原因,而实际上是另一个变量在影响该预测变量。
数值预测变量与响应变量之间的线性关系
在保持其他预测变量不变的情况下,每个数值预测变量必须与响应变量 $y$ 线性相关。如果不满足此条件,则不应将该预测变量包含在模型中。检查此条件最推荐的方法是绘制模型残差与每个预测变量的关系图。如果关系是线性的,残差将随机分布在零附近。这些分析只是近似的,因为无法在保持其他预测变量不变的情况下确定关系是否真正是线性的。
响应变量的正态分布
响应变量必须服从正态分布。为了验证这一点,通常使用直方图、正态分位图或正态性假设检验。
响应变量的方差恒定(同方差性)
响应变量的方差必须在预测变量的整个范围内保持恒定。为了验证这一点,通常绘制模型残差与每个预测变量的关系图。如果方差恒定,残差将随机分散,离散度一致且没有特定模式。锥形分布是缺乏同方差性的明显标志。也可以使用同方差性检验,如 Breusch-Pagan 检验。
此条件的原因如下:线性模型假设响应变量($y$)服从正态分布,其均值($\mu$)可以建模为其他变量(预测变量)的函数,其方差($\sigma$)使用离散常数和函数 $\nu(\mu)$ 计算。这意味着方差不是直接建模为预测变量的函数,而是通过其与均值的关系间接建模,并且是一个唯一值。
$$\hat{\sigma}^2 = \frac{\sum^n_{i=1} \hat{\epsilon}_i^2}{n-p} = \frac{\sum^n_{i=1} (y_i - \hat{\mu})^2}{n-p}$$这在实践中有什么影响?虽然这些模型获得的均值估计很好,但与之相关的不确定性,以及可以计算的置信区间和预测区间,可能不太准确。
无自相关(独立性)
每个观测值的值必须独立于其他观测值。建议按记录观测值的时间顺序绘制残差图。如果存在任何模式,这可能表明存在自相关。也可以使用 Durbin-Watson 假设检验来检查自相关。
异常值、高杠杆点或强影响点
识别异常值或可能影响模型的观测值非常重要。检测它们最简单的方法是通过残差(更多细节见后文)。
样本大小
这本身不是一个条件,但如果观测值不够多,实际上没有真正影响力的预测变量可能显得有影响。常见的建议是观测值的数量应至少是模型中预测变量数量的 10 到 20 倍。
简约性(奥卡姆剃刀)
这个术语指的是最佳模型是能够用最少的预测变量解释响应变量中观测到的变异性的模型,因此假设最少。
绝大多数条件都是使用残差来验证的,因此通常先生成模型,然后验证条件。实际上,拟合模型应该被视为一个迭代过程,在此过程中调整模型、评估其残差并进行改进。这一过程持续进行,直到达到最优模型。
异常值¶
无论模型是否被接受,始终建议识别任何潜在的异常值、高杠杆观测值或强影响点,因为它们可能会显著影响模型。是否删除此类观测值的决定应根据模型的目的仔细考虑。如果目标是预测,不含异常值或强影响观测值的模型通常能更好地预测大多数情况。然而,关注这些值非常重要,因为如果它们不是测量误差,它们可能代表最有趣的案例。当怀疑存在异常值或强影响点时,正确的做法是分别拟合包含和不包含该值的回归模型。
简单线性回归示例¶
假设一位体育分析师想知道棒球队球员的击球次数与得分之间是否存在关系。如果存在这种关系并且可以建立模型,该模型可用于预测比赛结果。
库¶
本示例使用的库:
# 数据管理
# ==============================================================================
import pandas as pd
# 绘图
# ==============================================================================
import matplotlib.pyplot as plt
# 预处理和建模
# ==============================================================================
from scipy.stats import pearsonr
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error
import statsmodels.api as sm
# Matplotlib 配置
# ==============================================================================
plt.style.use('fivethirtyeight')
plt.rcParams.update({'font.size': 10, 'lines.linewidth': 1.5})
# 警告配置
# ==============================================================================
import warnings
warnings.filterwarnings('once')
数据¶
# 数据
# ==============================================================================
teams = ["Texas","Boston","Detroit","Kansas","St.","New_S.","New_Y.",
"Milwaukee","Colorado","Houston","Baltimore","Los_An.","Chicago",
"Cincinnati","Los_P.","Philadelphia","Chicago","Cleveland","Arizona",
"Toronto","Minnesota","Florida","Pittsburgh","Oakland","Tampa",
"Atlanta","Washington","San.F","San.I","Seattle"]
hits = [5659, 5710, 5563, 5672, 5532, 5600, 5518, 5447, 5544, 5598,
5585, 5436, 5549, 5612, 5513, 5579, 5502, 5509, 5421, 5559,
5487, 5508, 5421, 5452, 5436, 5528, 5441, 5486, 5417, 5421]
runs = [855, 875, 787, 730, 762, 718, 867, 721, 735, 615, 708, 644, 654, 735,
667, 713, 654, 704, 731, 743, 619, 625, 610, 645, 707, 641, 624, 570,
593, 556]
data = pd.DataFrame({'team': teams, 'hits': hits, 'runs': runs})
data.head(3)
| team | hits | runs | |
|---|---|---|---|
| 0 | Texas | 5659 | 855 |
| 1 | Boston | 5710 | 875 |
| 2 | Detroit | 5563 | 787 |
探索性数据分析¶
在生成简单回归模型之前,第一步是可视化数据,以直观评估是否存在关系,并使用相关系数量化这种关系。
# 绘图
# ==============================================================================
fig, ax = plt.subplots(figsize=(4, 3))
data.plot(
x = 'hits',
y = 'runs',
c = 'firebrick',
kind = "scatter",
ax = ax
)
ax.set_title('击球次数与得分的分布');
# 两个变量之间的线性相关
# ==============================================================================
corr_test = pearsonr(x=data["hits"], y=data["runs"])
print(f"相关系数:{corr_test[0]}")
print(f"P 值:{corr_test[1]}")
相关系数:0.6106270467206688 P 值:0.00033883513597919785
图表和相关性检验显示存在线性关系,具有相当大的强度(r = 0.61)和显著性(p 值 = 0.000339)。有理由尝试生成一个线性回归模型,目标是根据球队的击球次数预测得分。
模型拟合¶
使用 runs(得分)作为响应变量,hits(击球次数)作为预测变量来拟合模型。与任何预测研究一样,不仅要拟合模型,还要量化其预测新观测值的能力。为了评估这一点,将数据分为两组:训练集和测试集。
Scikit-learn¶
# 数据划分为训练集和测试集
# ==============================================================================
X = data[['hits']]
y = data['runs']
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
train_size = 0.8,
random_state = 1234,
shuffle = True
)
# 创建和拟合模型
# ==============================================================================
model = LinearRegression()
model.fit(X=X_train, y=y_train)
LinearRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| fit_intercept | True | |
| copy_X | True | |
| tol | 1e-06 | |
| n_jobs | None | |
| positive | False |
# 模型信息
# ==============================================================================
print(f"截距:{model.intercept_}")
print(f"系数:{list(zip(model.feature_names_in_, model.coef_))}")
print(f"决定系数 R^2:{model.score(X, y)}")
截距:-2367.702841302211
系数:[('hits', np.float64(0.5528713534479736))]
决定系数 R^2:0.3586119899498744
模型训练完成后,使用测试集评估其预测能力。
# 测试集上的预测误差(rmse)
# ==============================================================================
predictions = model.predict(X=X_test)
rmse = root_mean_squared_error(y_true=y_test, y_pred=predictions)
print(f"前五个预测值:{predictions[0:5]}")
print(f"测试集误差(rmse):{rmse}")
前五个预测值:[643.78742093 720.0836677 690.78148597 789.19258689 627.20128033] 测试集误差(rmse):59.336716083360486
Statsmodels¶
Statsmodels 的线性回归实现比 Scikit-learn 更完整,因为它不仅拟合模型,还允许计算统计检验和验证此类模型所基于条件所需的分析。Statsmodels 有两种训练模型的方式:
指定模型公式,并将训练数据作为包含响应变量和预测变量的 dataframe 传递。此方法类似于 R 中使用的方法。
传递两个矩阵,一个用于预测变量,另一个用于响应变量。这与 Scikit-learn 使用的方法相同,区别在于预测变量矩阵必须包含额外的一列 1。
# 数据划分为训练集和测试集
# ==============================================================================
X = data[['hits']]
y = data['runs']
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
train_size = 0.8,
random_state = 1234,
shuffle = True
)
# 创建和拟合模型
# ==============================================================================
# 在矩阵开头添加一列 1 用于截距
X_train = sm.add_constant(X_train, prepend=True)
model = sm.OLS(endog=y_train, exog=X_train)
model = model.fit()
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: runs R-squared: 0.271
Model: OLS Adj. R-squared: 0.238
Method: Least Squares F-statistic: 8.191
Date: Sat, 29 Nov 2025 Prob (F-statistic): 0.00906
Time: 19:36:39 Log-Likelihood: -134.71
No. Observations: 24 AIC: 273.4
Df Residuals: 22 BIC: 275.8
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -2367.7028 1066.357 -2.220 0.037 -4579.192 -156.214
hits 0.5529 0.193 2.862 0.009 0.152 0.953
==============================================================================
Omnibus: 5.033 Durbin-Watson: 1.902
Prob(Omnibus): 0.081 Jarque-Bera (JB): 3.170
Skew: 0.829 Prob(JB): 0.205
Kurtosis: 3.650 Cond. No. 4.17e+05
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 4.17e+05. This might indicate that there are
strong multicollinearity or other numerical problems.
系数的置信区间¶
# 模型系数的置信区间
# ==============================================================================
intervals = model.conf_int(alpha=0.05)
intervals.columns = ['2.5%', '97.5%']
intervals
| 2.5% | 97.5% | |
|---|---|---|
| const | -4579.192050 | -156.213633 |
| hits | 0.152244 | 0.953499 |
预测¶
模型训练完成后,可以对新数据进行预测。Statsmodels 模型允许以两种方式计算预测:
.predict():仅返回预测值。.get_prediction().summary_frame():返回预测值以及相关的置信区间。
# 带有 95% 置信区间的预测
# ==============================================================================
predicctions = model.get_prediction(exog=X_train).summary_frame(alpha=0.05)
predicctions.head(4)
| mean | mean_se | mean_ci_lower | mean_ci_upper | obs_ci_lower | obs_ci_upper | |
|---|---|---|---|---|---|---|
| 3 | 768.183475 | 32.658268 | 700.454374 | 835.912577 | 609.456054 | 926.910897 |
| 23 | 646.551778 | 19.237651 | 606.655332 | 686.448224 | 497.558860 | 795.544695 |
| 14 | 680.276930 | 14.186441 | 650.856053 | 709.697807 | 533.741095 | 826.812765 |
| 13 | 735.011194 | 22.767596 | 687.794091 | 782.228298 | 583.893300 | 886.129088 |
模型的图形表示¶
除了最小二乘线之外,建议包含置信区间的上限和下限。这有助于识别根据生成的模型和给定的置信水平,响应变量平均值预期所在的区域。
# 带有 95% 置信区间的预测
# ==============================================================================
predicctions = model.get_prediction(exog=X_train).summary_frame(alpha=0.05)
predicctions['x'] = X_train.loc[:, 'hits']
predicctions['y'] = y_train
predicctions = predicctions.sort_values('x')
# 绘图
# ==============================================================================
fig, ax = plt.subplots(figsize=(6, 3.84))
ax.scatter(predicctions['x'], predicctions['y'], marker='o', color = "gray")
ax.plot(predicctions['x'], predicctions["mean"], linestyle='-', label="OLS")
ax.plot(predicctions['x'], predicctions["mean_ci_lower"], linestyle='--', color='blue', label="95% 置信区间")
ax.plot(predicctions['x'], predicctions["mean_ci_upper"], linestyle='--', color='blue')
ax.fill_between(predicctions['x'], predicctions["mean_ci_lower"], predicctions["mean_ci_upper"], alpha=0.3)
ax.legend();
测试误差¶
# 测试集上的误差
# ==============================================================================
X_test = sm.add_constant(X_test, prepend=True)
predictions = model.predict(exog=X_test)
rmse = root_mean_squared_error(y_true=y_test, y_pred=predictions)
print(f"测试集误差(rmse):{rmse}")
测试集误差(rmse):59.33671608336119
解释¶
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: runs R-squared: 0.271
Model: OLS Adj. R-squared: 0.238
Method: Least Squares F-statistic: 8.191
Date: Sat, 29 Nov 2025 Prob (F-statistic): 0.00906
Time: 19:36:40 Log-Likelihood: -134.71
No. Observations: 24 AIC: 273.4
Df Residuals: 22 BIC: 275.8
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -2367.7028 1066.357 -2.220 0.037 -4579.192 -156.214
hits 0.5529 0.193 2.862 0.009 0.152 0.953
==============================================================================
Omnibus: 5.033 Durbin-Watson: 1.902
Prob(Omnibus): 0.081 Jarque-Bera (JB): 3.170
Skew: 0.829 Prob(JB): 0.205
Kurtosis: 3.650 Cond. No. 4.17e+05
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 4.17e+05. This might indicate that there are
strong multicollinearity or other numerical problems.
coef 列返回线性模型方程两个参数的估计值($\hat{\beta}_0$ 和 $\hat{\beta}_1$),分别对应于截距(intercept 或 const)和斜率。
还显示了每个参数的标准误差、t 统计量值和双侧 p 值。这使我们能够确定预测变量是否显著不同于 0,即它们在模型中是否重要。对于生成的模型,截距和斜率都是显著的(p 值 < 0.05)。
R-squared 值表明模型能够解释响应变量(runs)中观测到的 27.1% 的变异性。此外,F 检验获得的 p 值(Prob (F-statistic) = 0.00906)表明有证据表明模型解释的方差大于随机预期(总方差)。
生成的线性模型遵循以下方程:
$$\text{runs = -2367.7028 + 0.5529 hits}$$每增加一个单位的击球次数,得分平均增加 0.5529 个单位。
模型的测试误差为 59.34。最终模型的预测值与实际值平均偏差为 59.34 个单位。
多元线性回归示例¶
假设一家公司的销售部门想研究不同渠道广告对产品销售数量的影响。现有一个数据集,包含 200 个地区的销售收入(以百万计),以及每个地区在广播、电视和报纸广告上分配的预算(也以百万计)。
库¶
本示例使用的库:
# 数据处理
# ==============================================================================
import pandas as pd
import numpy as np
# 绘图
# ==============================================================================
import matplotlib.pyplot as plt
import seaborn as sns
# 预处理和建模
# ==============================================================================
from scipy.stats import pearsonr
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.stats.anova import anova_lm
from scipy import stats
# Matplotlib 配置
# ==============================================================================
plt.style.use('fivethirtyeight')
plt.rcParams.update({'font.size': 10, 'lines.linewidth': 1.5})
# 警告配置
# ==============================================================================
import warnings
warnings.filterwarnings('ignore')
数据¶
# 数据
# ==============================================================================
tv = [230.1, 44.5, 17.2, 151.5, 180.8, 8.7, 57.5, 120.2, 8.6, 199.8, 66.1, 214.7,
23.8, 97.5, 204.1, 195.4, 67.8, 281.4, 69.2, 147.3, 218.4, 237.4, 13.2,
228.3, 62.3, 262.9, 142.9, 240.1, 248.8, 70.6, 292.9, 112.9, 97.2, 265.6,
95.7, 290.7, 266.9, 74.7, 43.1, 228.0, 202.5, 177.0, 293.6, 206.9, 25.1,
175.1, 89.7, 239.9, 227.2, 66.9, 199.8, 100.4, 216.4, 182.6, 262.7, 198.9,
7.3, 136.2, 210.8, 210.7, 53.5, 261.3, 239.3, 102.7, 131.1, 69.0, 31.5,
139.3, 237.4, 216.8, 199.1, 109.8, 26.8, 129.4, 213.4, 16.9, 27.5, 120.5,
5.4, 116.0, 76.4, 239.8, 75.3, 68.4, 213.5, 193.2, 76.3, 110.7, 88.3, 109.8,
134.3, 28.6, 217.7, 250.9, 107.4, 163.3, 197.6, 184.9, 289.7, 135.2, 222.4,
296.4, 280.2, 187.9, 238.2, 137.9, 25.0, 90.4, 13.1, 255.4, 225.8, 241.7, 175.7,
209.6, 78.2, 75.1, 139.2, 76.4, 125.7, 19.4, 141.3, 18.8, 224.0, 123.1, 229.5,
87.2, 7.8, 80.2, 220.3, 59.6, 0.7, 265.2, 8.4, 219.8, 36.9, 48.3, 25.6, 273.7,
43.0, 184.9, 73.4, 193.7, 220.5, 104.6, 96.2, 140.3, 240.1, 243.2, 38.0, 44.7,
280.7, 121.0, 197.6, 171.3, 187.8, 4.1, 93.9, 149.8, 11.7, 131.7, 172.5, 85.7,
188.4, 163.5, 117.2, 234.5, 17.9, 206.8, 215.4, 284.3, 50.0, 164.5, 19.6, 168.4,
222.4, 276.9, 248.4, 170.2, 276.7, 165.6, 156.6, 218.5, 56.2, 287.6, 253.8, 205.0,
139.5, 191.1, 286.0, 18.7, 39.5, 75.5, 17.2, 166.8, 149.7, 38.2, 94.2, 177.0,
283.6, 232.1]
radio = [37.8, 39.3, 45.9, 41.3, 10.8, 48.9, 32.8, 19.6, 2.1, 2.6, 5.8, 24.0, 35.1,
7.6, 32.9, 47.7, 36.6, 39.6, 20.5, 23.9, 27.7, 5.1, 15.9, 16.9, 12.6, 3.5,
29.3, 16.7, 27.1, 16.0, 28.3, 17.4, 1.5, 20.0, 1.4, 4.1, 43.8, 49.4, 26.7,
37.7, 22.3, 33.4, 27.7, 8.4, 25.7, 22.5, 9.9, 41.5, 15.8, 11.7, 3.1, 9.6,
41.7, 46.2, 28.8, 49.4, 28.1, 19.2, 49.6, 29.5, 2.0, 42.7, 15.5, 29.6, 42.8,
9.3, 24.6, 14.5, 27.5, 43.9, 30.6, 14.3, 33.0, 5.7, 24.6, 43.7, 1.6, 28.5,
29.9, 7.7, 26.7, 4.1, 20.3, 44.5, 43.0, 18.4, 27.5, 40.6, 25.5, 47.8, 4.9,
1.5, 33.5, 36.5, 14.0, 31.6, 3.5, 21.0, 42.3, 41.7, 4.3, 36.3, 10.1, 17.2,
34.3, 46.4, 11.0, 0.3, 0.4, 26.9, 8.2, 38.0, 15.4, 20.6, 46.8, 35.0, 14.3,
0.8, 36.9, 16.0, 26.8, 21.7, 2.4, 34.6, 32.3, 11.8, 38.9, 0.0, 49.0, 12.0,
39.6, 2.9, 27.2, 33.5, 38.6, 47.0, 39.0, 28.9, 25.9, 43.9, 17.0, 35.4, 33.2,
5.7, 14.8, 1.9, 7.3, 49.0, 40.3, 25.8, 13.9, 8.4, 23.3, 39.7, 21.1, 11.6, 43.5,
1.3, 36.9, 18.4, 18.1, 35.8, 18.1, 36.8, 14.7, 3.4, 37.6, 5.2, 23.6, 10.6, 11.6,
20.9, 20.1, 7.1, 3.4, 48.9, 30.2, 7.8, 2.3, 10.0, 2.6, 5.4, 5.7, 43.0, 21.3, 45.1,
2.1, 28.7, 13.9, 12.1, 41.1, 10.8, 4.1, 42.0, 35.6, 3.7, 4.9, 9.3, 42.0, 8.6]
newspaper = [69.2, 45.1, 69.3, 58.5, 58.4, 75.0, 23.5, 11.6, 1.0, 21.2, 24.2, 4.0,
65.9, 7.2, 46.0, 52.9, 114.0, 55.8, 18.3, 19.1, 53.4, 23.5, 49.6, 26.2,
18.3, 19.5, 12.6, 22.9, 22.9, 40.8, 43.2, 38.6, 30.0, 0.3, 7.4, 8.5, 5.0,
45.7, 35.1, 32.0, 31.6, 38.7, 1.8, 26.4, 43.3, 31.5, 35.7, 18.5, 49.9,
36.8, 34.6, 3.6, 39.6, 58.7, 15.9, 60.0, 41.4, 16.6, 37.7, 9.3, 21.4, 54.7,
27.3, 8.4, 28.9, 0.9, 2.2, 10.2, 11.0, 27.2, 38.7, 31.7, 19.3, 31.3, 13.1,
89.4, 20.7, 14.2, 9.4, 23.1, 22.3, 36.9, 32.5, 35.6, 33.8, 65.7, 16.0, 63.2,
73.4, 51.4, 9.3, 33.0, 59.0, 72.3, 10.9, 52.9, 5.9, 22.0, 51.2, 45.9, 49.8,
100.9, 21.4, 17.9, 5.3, 59.0, 29.7, 23.2, 25.6, 5.5, 56.5, 23.2, 2.4, 10.7,
34.5, 52.7, 25.6, 14.8, 79.2, 22.3, 46.2, 50.4, 15.6, 12.4, 74.2, 25.9, 50.6,
9.2, 3.2, 43.1, 8.7, 43.0, 2.1, 45.1, 65.6, 8.5, 9.3, 59.7, 20.5, 1.7, 12.9,
75.6, 37.9, 34.4, 38.9, 9.0, 8.7, 44.3, 11.9, 20.6, 37.0, 48.7, 14.2, 37.7,
9.5, 5.7, 50.5, 24.3, 45.2, 34.6, 30.7, 49.3, 25.6, 7.4, 5.4, 84.8, 21.6, 19.4,
57.6, 6.4, 18.4, 47.4, 17.0, 12.8, 13.1, 41.8, 20.3, 35.2, 23.7, 17.6, 8.3,
27.4, 29.7, 71.8, 30.0, 19.6, 26.6, 18.2, 3.7, 23.4, 5.8, 6.0, 31.6, 3.6, 6.0,
13.8, 8.1, 6.4, 66.2, 8.7]
sells = [22.1, 10.4, 9.3, 18.5, 12.9, 7.2, 11.8, 13.2, 4.8, 10.6, 8.6, 17.4, 9.2, 9.7,
19.0, 22.4, 12.5, 24.4, 11.3, 14.6, 18.0, 12.5, 5.6, 15.5, 9.7, 12.0, 15.0, 15.9,
18.9, 10.5, 21.4, 11.9, 9.6, 17.4, 9.5, 12.8, 25.4, 14.7, 10.1, 21.5, 16.6, 17.1,
20.7, 12.9, 8.5, 14.9, 10.6, 23.2, 14.8, 9.7, 11.4, 10.7, 22.6, 21.2, 20.2, 23.7,
5.5, 13.2, 23.8, 18.4, 8.1, 24.2, 15.7, 14.0, 18.0, 9.3, 9.5, 13.4, 18.9, 22.3,
18.3, 12.4, 8.8, 11.0, 17.0, 8.7, 6.9, 14.2, 5.3, 11.0, 11.8, 12.3, 11.3, 13.6,
21.7, 15.2, 12.0, 16.0, 12.9, 16.7, 11.2, 7.3, 19.4, 22.2, 11.5, 16.9, 11.7, 15.5,
25.4, 17.2, 11.7, 23.8, 14.8, 14.7, 20.7, 19.2, 7.2, 8.7, 5.3, 19.8, 13.4, 21.8,
14.1, 15.9, 14.6, 12.6, 12.2, 9.4, 15.9, 6.6, 15.5, 7.0, 11.6, 15.2, 19.7, 10.6,
6.6, 8.8, 24.7, 9.7, 1.6, 12.7, 5.7, 19.6, 10.8, 11.6, 9.5, 20.8, 9.6, 20.7, 10.9,
19.2, 20.1, 10.4, 11.4, 10.3, 13.2, 25.4, 10.9, 10.1, 16.1, 11.6, 16.6, 19.0, 15.6,
3.2, 15.3, 10.1, 7.3, 12.9, 14.4, 13.3, 14.9, 18.0, 11.9, 11.9, 8.0, 12.2, 17.1,
15.0, 8.4, 14.5, 7.6, 11.7, 11.5, 27.0, 20.2, 11.7, 11.8, 12.6, 10.5, 12.2, 8.7,
26.2, 17.6, 22.6, 10.3, 17.3, 15.9, 6.7, 10.8, 9.9, 5.9, 19.6, 17.3, 7.6, 9.7, 12.8,
25.5, 13.4]
data = pd.DataFrame({'tv': tv, 'radio': radio, 'newspaper': newspaper, 'sells': sells})
变量之间的关系¶
建立多元线性模型的第一步是研究变量之间的关系。这些信息对于识别模型的最佳预测变量和检测预测变量之间的共线性至关重要。此外,建议可视化每个变量的分布。
# 数值列之间的相关性
# ==============================================================================
def tidy_corr_matrix(corr_mat):
'''
将 pandas 相关矩阵转换为整洁格式的函数
'''
corr_mat = corr_mat.stack().reset_index()
corr_mat.columns = ['variable_1', 'variable_2','r']
corr_mat = corr_mat.loc[corr_mat['variable_1'] != corr_mat['variable_2'], :]
corr_mat['abs_r'] = np.abs(corr_mat['r'])
corr_mat = corr_mat.sort_values('abs_r', ascending=False)
return corr_mat
corr_matrix = data.select_dtypes(include=['float64', 'int']).corr(method='pearson')
tidy_corr_matrix(corr_matrix).head(10)
| variable_1 | variable_2 | r | abs_r | |
|---|---|---|---|---|
| 3 | tv | sells | 0.782224 | 0.782224 |
| 12 | sells | tv | 0.782224 | 0.782224 |
| 7 | radio | sells | 0.576223 | 0.576223 |
| 13 | sells | radio | 0.576223 | 0.576223 |
| 9 | newspaper | radio | 0.354104 | 0.354104 |
| 6 | radio | newspaper | 0.354104 | 0.354104 |
| 14 | sells | newspaper | 0.228299 | 0.228299 |
| 11 | newspaper | sells | 0.228299 | 0.228299 |
| 2 | tv | newspaper | 0.056648 | 0.056648 |
| 8 | newspaper | tv | 0.056648 | 0.056648 |
# 相关矩阵热力图
# ==============================================================================
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(4, 4))
sns.heatmap(
corr_matrix,
annot = True,
cbar = False,
annot_kws = {"size": 8},
vmin = -1,
vmax = 1,
center = 0,
cmap = sns.diverging_palette(20, 220, n=200),
square = True,
ax = ax
)
ax.set_xticklabels(
ax.get_xticklabels(),
rotation = 45,
horizontalalignment = 'right',
)
ax.tick_params(labelsize = 10)
# 数值变量分布
# ==============================================================================
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(7, 4))
axes = axes.flat
numeric_cols = data.select_dtypes(include=['float64', 'int']).columns
for i, colum in enumerate(numeric_cols):
sns.histplot(
data = data,
x = colum,
stat = "count",
kde = True,
color = (list(plt.rcParams['axes.prop_cycle']) * 2)[i]["color"],
line_kws= {'linewidth': 2},
alpha = 0.3,
ax = axes[i]
)
axes[i].set_title(colum, fontsize = 8, fontweight = "bold")
axes[i].tick_params(labelsize = 8)
axes[i].set_xlabel("")
axes[i].set_ylabel("")
fig.tight_layout()
plt.subplots_adjust(top = 0.9)
fig.suptitle('数值变量分布', fontsize = 10, fontweight = "bold");
模型拟合¶
拟合一个多元线性模型,目标是根据三个广告渠道的投资预测销售额。
# 数据划分
# ==============================================================================
X = data[['tv', 'radio', 'newspaper']]
y = data['sells']
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
train_size = 0.8,
random_state = 1234,
shuffle = True
)
# 创建和拟合模型
# ==============================================================================
# 在矩阵开头添加一列 1 用于截距
X_train = sm.add_constant(X_train, prepend=True)
model = sm.OLS(endog=y_train, exog=X_train,)
model = model.fit()
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: sells R-squared: 0.894
Model: OLS Adj. R-squared: 0.892
Method: Least Squares F-statistic: 437.8
Date: Sat, 29 Nov 2025 Prob (F-statistic): 1.01e-75
Time: 19:36:42 Log-Likelihood: -308.29
No. Observations: 160 AIC: 624.6
Df Residuals: 156 BIC: 636.9
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 2.8497 0.365 7.803 0.000 2.128 3.571
tv 0.0456 0.002 28.648 0.000 0.042 0.049
radio 0.1893 0.009 20.024 0.000 0.171 0.208
newspaper 0.0024 0.007 0.355 0.723 -0.011 0.016
==============================================================================
Omnibus: 53.472 Durbin-Watson: 2.153
Prob(Omnibus): 0.000 Jarque-Bera (JB): 147.411
Skew: -1.353 Prob(JB): 9.77e-33
Kurtosis: 6.846 Cond. No. 472.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
包含所有变量作为预测变量的模型具有较高的 $R^2$(0.894),这意味着它能够解释销售额中观测到的 89.4% 的变异性。模型的 p 值是显著的(1.01e-75),因此我们可以接受该模型比随机预期更好,并且至少有一个偏回归系数不同于 0。
根据 newspaper 偏回归系数获得的 p 值(0.723),该变量在其他预测变量存在的情况下对模型没有显著贡献。重新训练模型,但这次排除预测变量 newspaper。
# 从训练集和测试集中删除 newspaper 列
# ==============================================================================
X_train = X_train.drop(columns = 'newspaper')
X_test = X_test.drop(columns = 'newspaper')
X_train = sm.add_constant(X_train, prepend=True)
model = sm.OLS(endog=y_train, exog=X_train,)
model = model.fit()
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: sells R-squared: 0.894
Model: OLS Adj. R-squared: 0.892
Method: Least Squares F-statistic: 660.3
Date: Sat, 29 Nov 2025 Prob (F-statistic): 3.69e-77
Time: 19:36:42 Log-Likelihood: -308.36
No. Observations: 160 AIC: 622.7
Df Residuals: 157 BIC: 631.9
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 2.9004 0.335 8.652 0.000 2.238 3.563
tv 0.0456 0.002 28.751 0.000 0.042 0.049
radio 0.1904 0.009 21.435 0.000 0.173 0.208
==============================================================================
Omnibus: 54.901 Durbin-Watson: 2.157
Prob(Omnibus): 0.000 Jarque-Bera (JB): 156.962
Skew: -1.375 Prob(JB): 8.24e-35
Kurtosis: 6.998 Cond. No. 429.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
系数的置信区间¶
# 模型系数的置信区间
# ==============================================================================
intervals = model.conf_int(alpha=0.05)
intervals.columns = ['2.5%', '97.5%']
intervals
| 2.5% | 97.5% | |
|---|---|---|
| const | 2.238211 | 3.562549 |
| tv | 0.042439 | 0.048701 |
| radio | 0.172853 | 0.207942 |
残差诊断¶
# 训练预测的误差(残差)诊断
# ==============================================================================
predictions_train = model.predict(exog=X_train)
residuos_train = predictions_train - y_train
可视化检查¶
# 绘图
# ==============================================================================
fig, axes = plt.subplots(nrows=3, ncols=2, figsize=(8, 8))
axes[0, 0].scatter(y_train, predictions_train, edgecolors=(0, 0, 0), alpha = 0.4)
axes[0, 0].plot([y_train.min(), y_train.max()], [y_train.min(), y_train.max()], 'k--', color = 'black', lw=2)
axes[0, 0].set_title('预测值 vs 实际值', fontsize = 10, fontweight = "bold")
axes[0, 0].set_xlabel('实际值')
axes[0, 0].set_ylabel('预测值')
axes[0, 0].tick_params(labelsize = 7)
axes[0, 1].scatter(list(range(len(y_train))), residuos_train, edgecolors=(0, 0, 0), alpha = 0.4)
axes[0, 1].axhline(y = 0, linestyle = '--', color = 'black', lw=2)
axes[0, 1].set_title('残差', fontsize = 10, fontweight = "bold")
axes[0, 1].set_xlabel('id')
axes[0, 1].set_ylabel('残差')
axes[0, 1].tick_params(labelsize = 7)
sns.histplot(
data = residuos_train,
stat = "density",
kde = True,
line_kws= {'linewidth': 1},
alpha = 0.3,
ax = axes[1, 0]
)
axes[1, 0].set_title('残差分布', fontsize = 10, fontweight = "bold")
axes[1, 0].set_xlabel("残差")
axes[1, 0].tick_params(labelsize = 7)
sm.qqplot(
residuos_train,
fit = True,
line = 'q',
ax = axes[1, 1],
alpha = 0.4,
lw = 2
)
axes[1, 1].set_title('Q-Q 残差图', fontsize = 10, fontweight = "bold")
axes[1, 1].tick_params(labelsize = 7)
axes[2, 0].scatter(predictions_train, residuos_train, edgecolors=(0, 0, 0), alpha = 0.4)
axes[2, 0].axhline(y = 0, linestyle = '--', color = 'black', lw=2)
axes[2, 0].set_title('残差 vs 预测值', fontsize = 10, fontweight = "bold")
axes[2, 0].set_xlabel('预测值')
axes[2, 0].set_ylabel('残差')
axes[2, 0].tick_params(labelsize = 7)
# 删除空白图
fig.delaxes(axes[2, 1])
fig.tight_layout()
plt.subplots_adjust(top=0.9)
fig.suptitle('残差分析', fontsize = 12, fontweight = "bold");
残差似乎没有随机分布在零附近,变异性似乎在 X 轴上没有保持一致。这种模式表明缺乏同方差性和正态分布。
正态性检验¶
使用两种统计检验检验残差是否服从正态分布:Shapiro-Wilk 检验和 D'Agostino K 平方检验。后者包含在 statsmodels 摘要中,名为 Omnibus。
在这两种检验中,原假设假定数据服从正态分布。因此,如果 p 值不低于所选的显著性水平 alpha,则没有证据拒绝数据服从正态分布的假设。
# Shapiro-Wilk 检验
# ==============================================================================
shapiro_test = stats.shapiro(residuos_train)
shapiro_test
ShapiroResult(statistic=np.float64(0.9165122842956668), pvalue=np.float64(5.861065888990398e-08))
# D'Agostino K 平方检验
# ==============================================================================
k2, p_value = stats.normaltest(residuos_train)
print(f"统计量= {k2}, p 值 = {p_value}")
统计量= 54.90105653039115, p 值 = 1.197807558003796e-12
两个检验都提供了强有力的证据来拒绝数据服从正态分布的假设(p 值 << 0.01)。
预测¶
模型训练完成后,可以对新数据进行预测。Statsmodels 模型允许计算与每个预测相关的置信区间。
# 带有 95% 置信区间的预测
# ==============================================================================
predictions = model.get_prediction(exog=X_train).summary_frame(alpha=0.05)
predictions.head(4)
| mean | mean_se | mean_ci_lower | mean_ci_upper | obs_ci_lower | obs_ci_upper | |
|---|---|---|---|---|---|---|
| 146 | 15.231643 | 0.248325 | 14.741154 | 15.722132 | 11.880621 | 18.582665 |
| 32 | 7.615382 | 0.247198 | 7.127119 | 8.103645 | 4.264685 | 10.966079 |
| 43 | 13.928155 | 0.213535 | 13.506384 | 14.349927 | 10.586500 | 17.269810 |
| 99 | 17.001020 | 0.210052 | 16.586127 | 17.415913 | 13.660226 | 20.341814 |
测试集误差¶
# 测试误差
# ==============================================================================
X_test = sm.add_constant(X_test, prepend=True)
predictions = model.predict(exog = X_test)
rmse = root_mean_squared_error(y_true=y_test, y_pred=predictions)
print(f"测试集误差(rmse):{rmse}")
测试集误差(rmse):1.6956207500101192
解释¶
多元线性回归模型:
$$\text{sells = 2.9004 + 0.0456tv + 0.1904radio}$$能够解释销售额中观测到的 89.4% 的方差(R-squared: 0.894, Adj. R-squared: 0.892)。$F$ 检验是显著的(p 值: 3.69e-77),提供了明确的证据表明该模型比随机预期更好地解释了销售额的方差。每个变量的统计检验确认 tv 和 radio 与销售数量相关并对模型有贡献。
不满足正态性条件,因此为系数和预测估计的置信区间不可靠。
测试误差(rmse)为 1.696。最终模型的预测值与实际值平均偏差为 1.696 个单位。
预测变量之间的交互作用¶
得出结论所依据的线性模型假设,由于某一媒体渠道预算增加而对销售产生的影响独立于在其他渠道上的支出。例如,线性模型认为电视广告预算增加一个单位对销售的平均影响始终为 0.0456,无论广播广告上花费多少。然而,情况不一定如此——预测变量之间可能存在交互作用,使得每个预测变量对响应变量的影响在一定程度上取决于另一个预测变量的值。
如前所定义,具有两个预测变量的线性模型遵循以下方程:
$$y=\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2}+\epsilon$$根据此定义,预测变量 $x_1$ 增加一个单位会导致响应变量 y 平均增加 $\beta_{1}$。对预测变量 $x_2$ 的修改不会改变这一点,反之亦然。为了使模型考虑两者之间的交互作用,引入第三个预测变量,称为交互项,它是预测变量 $x_1$ 和 $x_2$ 的乘积。
$$y=\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2}+\beta_{3}x_{1}x_{2} + e$$重新整理各项得:
$$y=\beta_{0}+(\beta_{1} + \beta_{3}x_2)x_{1}+\beta_{2}x_{2}+ e$$现在,$x_{1}$ 对 $y$ 的影响不再是常数,而是取决于 $x_{2}$ 的值。
在包含预测变量之间交互作用的多元线性回归模型中,必须考虑层次原则。该原则规定,如果模型中包含预测变量之间的交互作用,则必须始终包含参与交互作用的各个预测变量,无论其 p 值是否显著。
在 statsmodels 中,可以通过两种方式引入预测变量之间的交互作用:
在公式中使用
*项指定:sells ~ tv * radio添加一个新列,包含要在模型中包含交互作用的预测变量的乘积。
# 数据划分
# ==============================================================================
X = data[['tv', 'radio']]
y = data['sells']
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
train_size = 0.8,
random_state = 1234,
shuffle = True
)
# 使用矩阵创建带有交互作用的模型
# ==============================================================================
# 添加交互项的新列
X_train['tv_radio'] = X_train['tv'] * X_train['radio']
X_test['tv_radio'] = X_test['tv'] * X_test['radio']
X_train = sm.add_constant(X_train, prepend=True)
model_interactions = sm.OLS(endog=y_train, exog=X_train,)
model_interactions = model_interactions.fit()
print(model_interactions.summary())
OLS Regression Results
==============================================================================
Dep. Variable: sells R-squared: 0.968
Model: OLS Adj. R-squared: 0.967
Method: Least Squares F-statistic: 1562.
Date: Sat, 29 Nov 2025 Prob (F-statistic): 4.28e-116
Time: 19:36:44 Log-Likelihood: -212.91
No. Observations: 160 AIC: 433.8
Df Residuals: 156 BIC: 446.1
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 6.9035 0.281 24.558 0.000 6.348 7.459
tv 0.0183 0.002 10.812 0.000 0.015 0.022
radio 0.0261 0.010 2.623 0.010 0.006 0.046
tv_radio 0.0011 5.86e-05 18.931 0.000 0.001 0.001
==============================================================================
Omnibus: 121.946 Durbin-Watson: 1.686
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1473.094
Skew: -2.642 Prob(JB): 0.00
Kurtosis: 16.894 Cond. No. 1.84e+04
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.84e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
结果显示有明确的证据表明交互项 tv radio 是显著的(p 值*非常接近 0)。
包含交互作用的模型的 调整后 R 方为 0.967,高于仅考虑预测变量个别影响的模型的 0.892。然而,这个差异是否足以声称包含交互作用的模型更优?回答这个问题的一种方法是使用 F 检验(ANOVA)。
使用 F 检验(ANOVA)比较模型¶
考虑一个模型 $M$ 和另一个较小的模型 $m$,后者由 $M$ 中包含的预测变量子集构成。如果拟合差异很小,根据简约性原则,模型 $m$ 更合适。可以通过比较残差来检验拟合差异是否显著。具体来说,使用的统计量是:
$$\frac{RSS_m - RSS_M}{RSS_M}$$为避免模型大小影响检验,每个模型的残差平方和 RSS 除以其自由度。得到的统计量服从 $F$ 分布:
$$\frac{(RSS_m - RSS_M)/(df_m - df_M)}{RSS_M/(df_M)} \sim F_{df_m-df_M, \ df_M}$$其中 $df$ 是模型的自由度,对应于观测数减去预测变量数。
在前面的部分,训练了一个包含交互作用的模型和一个不包含交互作用的模型。现在进行假设检验以评估原假设,即两个模型对数据的拟合程度相同。换句话说,确定一个模型在预测响应变量方面是否优于另一个模型。这可以使用 statsmodels.stats.anova 中的 anova_lm() 函数来完成。
anova_lm(model, model_interactions)
| df_resid | ssr | df_diff | ss_diff | F | Pr(>F) | |
|---|---|---|---|---|---|---|
| 0 | 157.0 | 442.212726 | 0.0 | NaN | NaN | NaN |
| 1 | 156.0 | 134.116584 | 1.0 | 308.096142 | 358.3673 | 2.926598e-42 |
ANOVA 检验提供了明确的证据(p 值几乎为零)表明包含预测变量之间交互作用的模型能够更好地建模响应变量。
这种比较模型的方法在统计学界已经得到广泛认可。在机器学习领域,更常见的是使用验证技术(如交叉验证)来比较模型。
杂项说明¶
在本节中,我收集了在不同来源中发现的评论、定义和说明,我认为最好将其作为补充信息保留。
最小二乘法和回归的起源¶
Linear Models with R, by Julian J. Faraway
最小二乘法由 Adrien Marie Legendre 于 1805 年发表。回归一词来自 Francis Galton 于 1885 年发表的一篇名为Regression to Mediocrity的论文。在该论文中,Galton 使用最小二乘法证明了高个子父母的孩子往往也很高,但没有父母那么高,而矮个子父母的孩子往往也较矮,但没有父母那么矮。
最小二乘线性模型方差的估计¶
Linear Models with R, by Julian J. Faraway
通过最小二乘法获得的线性模型的方差($\sigma^2$)估计为:
$$\sigma^2 = \frac{RSS}{n - p}$$残差标准误差(RSE)是 $\sigma^2$ 的平方根:
$$RSE = \sqrt{\frac{RSS}{n - p}}$$最小二乘法估计线性模型系数的优点¶
Linear Models with R, by Julian J. Faraway
虽然有替代最小二乘法来估计线性模型相关系数 $\hat{\beta}_j$ 的方法,但它具有几个优点:
它具有几何解释,使其更容易理解。
如果误差是独立且正态分布的,其解与最大似然估计等效。
$\hat{\beta}_j$ 是无偏估计。
可识别性或共线性¶
Linear Models with R, by Julian J. Faraway
只有当预测变量构成的矩阵具有满秩,即其所有列(预测变量)线性独立时,最小二乘法才有唯一解。在实践中,这种可识别性条件经常被违反。以下是发生这种情况的一些场景:
当模型中引入的预测变量之一是模型中已有的其他预测变量的线性变换或组合时。例如,如果同时以千克和磅引入体重变量,或者如果包含基础教育年数、大学教育年数和总教育年数等预测变量。可以通过研究可用变量的性质及其关系来避免此问题。
模型过饱和,即预测变量多于观测值。
通过假设检验评估残差正态性时的注意事项¶
Linear Models with R, by Julian J. Faraway
线性回归模型的残差服从正态分布是预测变量显著性(p 值)和置信区间(从理论模型计算)准确的必要条件。该条件通常通过假设检验(如 Shapiro-Wilk 检验)进行评估。在这种情况下,理解 p 值与样本大小之间的关系很重要。残差越多,检验的功效越大,因此正态性的小偏差会变得显著。此外,中心极限定理表明,随着样本量的增加,结果对正态性偏差变得更加稳健。鉴于这些特性,通常建议使用理论分位数-分位数图(qq-plot)以图形方式评估残差的正态性。
变量转换¶
Linear Models with R, by Julian J. Faraway 和 Wikipedia
转换响应变量或预测变量可以改善模型拟合或纠正某些回归假设的违反。
当对响应变量应用转换时,重要的是要记住模型生成的预测值是在转换后的尺度上。预测完成后,可以将其转换回原始尺度。置信区间也是如此:首先计算上限和下限,然后将其转换回来。相比之下,预测变量获得的回归系数必须在转换的上下文中解释。无法应用转换的逆变换并在原始尺度上解释它们。
Box-Cox 转换
响应变量的指数转换($y^{\lambda}$)通常是改善模型的有用解决方案。然而,识别最佳指数值并不总是简单的。Box-Cox 方法允许确定是否存在可以对响应变量进行幂运算以改善模型拟合的值,如果存在,则识别该值是什么。根据此方法,寻求一个转换 $y \rightarrow g_{\lambda}(y)$,使得:
$$ g_{\lambda}(y) = \begin{cases} \frac{y^{\lambda}-1}{\lambda} & \text{如果 } \lambda \neq 0 \\ \log(y) & \text{如果 } \lambda = 0 \end{cases} $$当模型的目标是预测时,$\frac{y^{\lambda}-1}{y}$ 可以简化为 $y^{\lambda}$。
最佳的 $\lambda$ 值通过最大似然法识别:选择一系列 $\lambda$ 值,对于每个值,应用转换并计算残差平方和。产生最小残差和的值是最佳选择。
响应变量的转换可能使模型更难解释,因此除非确实必要,否则不建议使用。为确保其必要性,除了计算最佳 $\lambda$ 值外,还可以估计其 95% 置信区间。如果此区间包含值 $\lambda=1$,则没有足够的证据支持转换。当转换是必要的时,建议选择置信区间内便于模型解释的值。例如,如果区间是 [-0.7, 0.7],值 0.5 最合适,因为它对应于 $\sqrt(y)$。
Box-Cox 转换仅适用于响应变量始终取正值的情况。如果任何 $y_i < 0$,可以向 $y$ 添加一个常数使其为正,但这是一个有些不优雅的解决方案。此转换的另一个特点是它高度受异常值影响,导致 $\lambda$ 的绝对值可疑地高。
对数转换
Box-Cox 指数转换有多种替代方案。其中一种是向响应变量添加常数然后应用对数:$g_{\alpha} = \log(y + \alpha)$。
线性模型中回归系数的解释¶
Linear Models with R, by Julian J. Faraway
当使用线性回归模型提取预测变量与响应变量之间关系的信息时,必须谨慎,避免得出超出模型所告诉我们的结论。
来自 faraway 包的 gala 数据集包含有关组成加拉帕戈斯群岛的岛屿信息。存储的变量包括:岛上栖息的物种数量(Species)、岛屿面积(Area)、海拔(Elevation)、到最近岛屿的距离(Nearest)、到圣克鲁斯岛的距离(Scruz)以及相邻岛屿的面积(Adjacent)。目标是使用线性回归模型研究预测变量 Elevation 与岛上物种数量之间的关系。
url = (
"https://raw.githubusercontent.com/JoaquinAmatRodrigo/Estadistica-machine-learning-python/"
"master/data/gala_faraway.csv"
)
data = pd.read_csv(url)
data.head(3)
| Island | Species | Endemics | Area | Elevation | Nearest | Scruz | Adjacent | |
|---|---|---|---|---|---|---|---|---|
| 0 | Baltra | 58 | 23 | 25.09 | 346 | 0.6 | 0.6 | 1.84 |
| 1 | Bartolome | 31 | 21 | 1.24 | 109 | 0.6 | 26.3 | 572.33 |
| 2 | Caldwell | 3 | 3 | 0.21 | 114 | 2.8 | 58.7 | 0.78 |
model = smf.ols(
formula = 'Species ~ Area + Elevation + Nearest + Scruz + Adjacent',
data = data
)
model = model.fit()
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Species R-squared: 0.766
Model: OLS Adj. R-squared: 0.717
Method: Least Squares F-statistic: 15.70
Date: Sat, 29 Nov 2025 Prob (F-statistic): 6.84e-07
Time: 19:36:45 Log-Likelihood: -162.54
No. Observations: 30 AIC: 337.1
Df Residuals: 24 BIC: 345.5
Df Model: 5
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 7.0682 19.154 0.369 0.715 -32.464 46.601
Area -0.0239 0.022 -1.068 0.296 -0.070 0.022
Elevation 0.3195 0.054 5.953 0.000 0.209 0.430
Nearest 0.0091 1.054 0.009 0.993 -2.166 2.185
Scruz -0.2405 0.215 -1.117 0.275 -0.685 0.204
Adjacent -0.0748 0.018 -4.226 0.000 -0.111 -0.038
==============================================================================
Omnibus: 12.683 Durbin-Watson: 2.476
Prob(Omnibus): 0.002 Jarque-Bera (JB): 13.498
Skew: 1.136 Prob(JB): 0.00117
Kurtosis: 5.374 Cond. No. 1.90e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.9e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
如果将回归系数解释为:Elevation 每增加一个单位,物种数量平均增加 0.3195 单位,这将是一个错误的结论。事实上,如果使用相同的数据拟合一个更简单的模型,系数值会发生变化。
model = smf.ols(
formula = 'Species ~ Elevation',
data = data
)
model = model.fit()
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Species R-squared: 0.545
Model: OLS Adj. R-squared: 0.529
Method: Least Squares F-statistic: 33.59
Date: Sat, 29 Nov 2025 Prob (F-statistic): 3.18e-06
Time: 19:36:45 Log-Likelihood: -172.49
No. Observations: 30 AIC: 349.0
Df Residuals: 28 BIC: 351.8
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 11.3351 19.205 0.590 0.560 -28.005 50.675
Elevation 0.2008 0.035 5.795 0.000 0.130 0.272
==============================================================================
Omnibus: 14.860 Durbin-Watson: 2.021
Prob(Omnibus): 0.001 Jarque-Bera (JB): 29.281
Skew: 0.878 Prob(JB): 4.38e-07
Kurtosis: 7.510 Cond. No. 741.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
这是因为给定预测变量的回归系数必须始终在模型中包含的其他预测变量的背景下进行解释,因为它们会相互影响。正确的解释是:在保持其他预测变量不变的情况下,预测变量 $x_j$ 增加一个单位会导致响应变量平均变化 $\hat{\beta}_j$ 个单位。
通常,当每个预测变量的测量尺度差异很大(数量级不同)时,在拟合模型之前会对预测变量进行标准化。在这种情况下,回归系数的解释变为:在保持其他预测变量不变的情况下,预测变量 $x_j$ 增加一个标准单位会导致响应变量平均变化 $\hat{\beta}_j$ 个标准单位。
在观察性研究中,研究者很少能够随意保持预测变量不变,这使得建立因果关系变得困难。
模型和预测变量显著性的置换检验(蒙特卡洛模拟)¶
Linear Models with R, by Julian J. Faraway
基于 F 检验 的假设检验依赖于残差服从正态分布的假设。虽然中心极限定理表明,即使分布偏离正态性,只要样本量足够大,推断结果仍然有效,但没有确切的样本量大小可以保证其有效性。置换检验提供了一种不需要假设残差正态性的替代方法。
假设我们有一个包含两个预测变量的模型 Species ~ Nearest + Scruz,计算其 F 统计量。相关的 p 值 表示在假设响应变量与预测变量之间没有关系的情况下,获得如此极端或更极端的 F 值的可能性。当满足条件 $\epsilon \sim N(0, \sigma^2)$ 时,这个概率可以从 F 分布 推导出来。
# 数据(来自R包faraway的gala数据集)
# ==============================================================================
url = (
"https://raw.githubusercontent.com/JoaquinAmatRodrigo/Estadistica-machine-learning-python/"
"master/data/gala_faraway.csv"
)
data = pd.read_csv(url)
# 模型
# ==============================================================================
model = smf.ols(formula = 'Species ~ Nearest + Scruz', data = data)
model = model.fit()
# F统计量和p值
# ==============================================================================
print(f"F统计量: {model.fvalue}")
print(f"P值: {model.f_pvalue}")
F统计量: 0.6019558326652168 P值: 0.5549254563908441
当不满足正态性条件时,这些值是不可靠的。更好的方法是使用置换检验。为此,通过在观测值之间随机交换响应变量来模拟"响应变量与所有预测变量之间不存在关联"的原假设。
如果这个过程重复足够多次(1000 - 10000次),每次都调整模型并存储 F 统计量,就可以计算 F 等于或大于初始模型中获得值的情况所占的百分比。这个百分比就是 p 值 的经验近似。
# 置换检验
# ==============================================================================
n_simulations = 5000
f_values = np.repeat(np.nan, n_simulations)
data_temp = data.copy()
for i in np.arange(n_simulations):
data_temp["Species"] = data['Species'].sample(frac=1).reset_index(drop=True)
model_temp = smf.ols(formula = 'Species ~ Nearest + Scruz', data = data_temp)
model_temp = model_temp.fit()
f_values[i] = model_temp.fvalue
p_value_empirico = np.mean(f_values >= 0.6019558326652213)
print(f"通过置换检验近似的p值: {p_value_empirico}")
通过置换检验近似的p值: 0.5546
通过置换检验获得的 p 值 与基于正态性的理论方法获得的值(0.555)非常相似。
置换方法的优点在于,当满足正态性条件时,它与理论方法一样好(如果执行足够多的置换),而且当不满足正态性条件时也可以应用。缺点是需要更多的计算量。
同样的置换方法可以用来确定某个特定预测变量是否对模型有显著贡献,换句话说,它是否与响应变量相关联。在这种情况下,只有感兴趣的预测变量的值被置换,从而模拟该预测变量与响应变量不存在关联的原假设。在每次置换中,拟合模型并存储该预测变量的 t 统计量。执行足够多的置换后,计算 t 的绝对值等于或大于初始模型中观察到的绝对值的情况所占的百分比。
假设有一个包含两个预测变量的模型 Species ~ Nearest + Scruz,我们想要计算预测变量 Scruz 的显著性。
# 模型
# ==============================================================================
model = smf.ols(formula = 'Species ~ Nearest + Scruz', data = data)
model = model.fit()
# T统计量和p值
# ==============================================================================
print(f"Scruz的t统计量: {model.tvalues['Scruz']}")
print(f"Scruz的p值: {model.pvalues['Scruz']}")
Scruz的t统计量: -1.0946730850617026 Scruz的p值: 0.2833295186486556
# 置换检验
# ==============================================================================
n_simulations = 5000
t_values = np.repeat(np.nan, n_simulations)
data_temp = data.copy()
for i in np.arange(n_simulations):
data_temp["Scruz"] = data['Scruz'].sample(frac=1).reset_index(drop=True)
model_temp = smf.ols(formula = 'Species ~ Nearest + Scruz', data = data_temp)
model_temp = model_temp.fit()
t_values[i] = model_temp.tvalues['Scruz']
p_value_empirico = np.mean(np.abs(t_values) >= np.abs(-1.094673085061703))
print(f"通过置换检验近似的p值: {p_value_empirico}")
通过置换检验近似的p值: 0.2674
通过置换检验获得的 p 值 与基于正态性的理论方法获得的值(0.2833)非常相似。
自助法 计算置信区间¶
Linear Models with R, by Julian J. Faraway
statsmodels 和 scikitlearn 用于计算线性模型回归系数置信区间的方法基于 t-student 分布,遵循以下结构:
为使基于此理论分布的区间有效,模型的残差需要服从正态分布。如果不满足这一条件,自助法(bootstrapping)方法提供了一种不需要此条件的替代方案。
以下是如何应用此方法估计模型 Species ~ Area + Elevation + Nearest + Scruz + Adjacent 的 95% 置信区间 的示例。
在 Julian J. Faraway 的《Linear Models with R》一书中,重采样是在模型的残差上进行的。在我看来,对(响应变量,预测变量)配对进行重采样更为直观。获得的置信区间估计值并不完全相同,因此我无法保证这种方法的有效性。
# 数据(来自R包faraway的gala数据集)
# ==============================================================================
url = (
"https://raw.githubusercontent.com/JoaquinAmatRodrigo/Estadistica-machine-learning-python/"
"master/data/gala_faraway.csv"
)
data = pd.read_csv(url)
# 系数和置信区间
# ==============================================================================
model = smf.ols(
formula = 'Species ~ Area + Elevation + Nearest + Scruz + Adjacent',
data = data
)
model = model.fit()
print("模型系数")
print(model.params)
print("")
print("置信区间")
print(model.conf_int(alpha=0.05))
模型系数
Intercept 7.068221
Area -0.023938
Elevation 0.319465
Nearest 0.009144
Scruz -0.240524
Adjacent -0.074805
dtype: float64
置信区间
0 1
Intercept -32.464101 46.600542
Area -0.070216 0.022339
Elevation 0.208710 0.430219
Nearest -2.166486 2.184774
Scruz -0.685093 0.204044
Adjacent -0.111336 -0.038273
# 通过自助法估计的区间
# ==============================================================================
n_simulations = 5000
# 6 = 5个预测变量 + 1个截距项
coef_values = np.zeros(shape= (n_simulations, 6), dtype=float)
for i in np.arange(n_simulations):
data_temp = data.sample(frac=1, replace=True)
model_temp = smf.ols(
formula = 'Species ~ Area + Elevation + Nearest + Scruz + Adjacent',
data = data_temp
)
model_temp = model_temp.fit()
coef_values[i, :] = model_temp.params
# 0.025和0.975分位数之间的区间
empirical_intervals = np.quantile(coef_values, q = [.025, 0.975], axis=0)
empirical_intervals = pd.DataFrame(
data = empirical_intervals,
index = ['2.5%', '97.5%'],
columns = model.conf_int().index
)
print("经验区间")
empirical_intervals
经验区间
| Intercept | Area | Elevation | Nearest | Scruz | Adjacent | |
|---|---|---|---|---|---|---|
| 2.5% | -30.167534 | -0.090166 | 0.049655 | -4.595607 | -0.636914 | -0.142089 |
| 97.5% | 35.610392 | 0.417148 | 0.502355 | 1.732540 | 0.335822 | 0.008955 |
稳健回归¶
前面章节描述的普通最小二乘(OLS)回归方法假设残差/误差是独立的、具有恒定方差且服从正态分布。在实践中,这些条件通常不能满足,因此需要有替代的拟合方法。其中一些方法包括稳健回归、广义最小二乘和加权最小二乘。
稳健回归
当误差不服从正态分布时,最小二乘法得到的结果会受到影响,尾部越长影响越大。一个简单的解决方案是消除形成这些尾部的异常值。然而,如果确认这些不是读数错误,模型应该包含它们,因为它们是所研究现象的一部分。稳健回归减少了异常值对模型拟合的影响。最常用的两种稳健回归类型是:M-估计和最小截断二乘。
M-估计:根据用于减少极端观测值权重的函数不同,有不同的变体。Huber 方法降低了异常值的影响,只要异常值数量较少且不是过于极端。
最小截断二乘:这种稳健回归通过使用最小二乘法拟合模型,但只使用 q 个最小的残差,完全忽略其余的观测值。因此,它比 M-估计 更独立于异常值,尽管它依赖于指定的 q 值。
在大多数情况下,使用稳健回归获得的结果与使用最小二乘法并分析异常或有影响力的观测值获得的结果相似。当后者的分析无法完成时,无论是因为研究者不知道如何做还是因为这是一个自动化过程,稳健回归更为安全。
鉴于这些调整方法可以快速应用,稳健回归可以用作确认方法。首先使用最小二乘法拟合模型,如果与稳健回归比较没有发现显著差异,则表明模型不包含有影响力的观测值。
广义最小二乘
这是当残差之间存在相关性时最小二乘回归的替代方法。这种情况在时间序列数据中经常发生。
加权最小二乘
这是一种不受残差方差不恒定(异方差性)影响的最小二乘回归替代方法。建议在以下情况使用:
当残差与某个预测变量成比例时,即随着预测变量值的增加,残差也随之增加。
当变量 $Y_i$ 从 $n_i$ 个观测值中获得时(例如,$n$ 次重复的平均值),方差可能与组大小成比例,即 $Var(y_i) = \sigma^2/n_i$。
当响应变量来自不同来源时,例如不同的仪器,每个仪器具有不同的精度,为每个来源 $i$ 分配一个权重,使得 $weight_i = 1/sd(y_i)$。
会话信息¶
import session_info
session_info.show(html=False)
----- matplotlib 3.10.7 numpy 2.2.6 pandas 2.3.3 scipy 1.15.3 seaborn 0.13.2 session_info v1.0.1 sklearn 1.7.2 statsmodels 0.14.5 ----- IPython 9.6.0 jupyter_client 7.4.9 jupyter_core 5.9.1 jupyterlab 4.5.0 notebook 6.5.7 ----- Python 3.13.9 | packaged by Anaconda, Inc. | (main, Oct 21 2025, 19:16:10) [GCC 11.2.0] Linux-6.14.0-36-generic-x86_64-with-glibc2.39 ----- Session information updated at 2025-11-29 19:39
参考文献¶
OpenIntro Statistics: Third Edition, David M Diez, Christopher D Barr, Mine Çetinkaya-Rundel
An Introduction to Statistical Learning: with Applications in R (Springer Texts in Statistics)
Linear Models with R, Julian J.Faraway
Points of Significance: Simple linear regression by Naomi Altman & Martin Krzywinski
Points of Significance: Multiple linear regression Martin Krzywinski & Naomi Altman
Métodos estadísticos en ingenieria Rafael Romero Villafranca, Luisa Rosa Zúnica Ramajo
Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825-2830, 2011.
引用¶
如何引用本文档
如果您使用本文档或其中任何部分,请注明出处,谢谢!
Linear Regression with Python by Joaquín Amat Rodrigo,根据知识共享署名-非商业性使用-相同方式共享4.0国际许可协议(CC BY-NC-SA 4.0 DEED)发布,网址:https://cienciadedata.net/documentos/py10-linear-regression-python-cn.html
您喜欢这篇文章吗?您的支持很重要
您的贡献将帮助我继续创作免费的教育内容。非常感谢!😊
本作品由 Joaquín Amat Rodrigo 和 Javier Escobar Ortiz 创作,根据知识共享署名-非商业性使用-相同方式共享4.0国际许可协议发布。
允许:
-
共享:以任何媒介或格式复制和再分发本材料。
-
改编:重新混合、转换和基于本材料进行创作。
须遵守以下条款:

