More about forecasting in cienciadedatos.net
- ARIMA and SARIMAX models with python
- Time series forecasting with machine learning
- Forecasting time series with gradient boosting: XGBoost, LightGBM and CatBoost
- Forecasting time series with XGBoost
- Global Forecasting Models: Multi-series forecasting
- Global Forecasting Models: Comparative Analysis of Single and Multi-Series Forecasting Modeling
- Probabilistic forecasting
- Forecasting with deep learning
- Forecasting energy demand with machine learning
- Forecasting web traffic with machine learning
- Intermittent demand forecasting
- Modelling time series trend with tree-based models
- Bitcoin price prediction with Python
- Stacking ensemble of machine learning models to improve forecasting
- Interpretable forecasting models
- Mitigating the Impact of Covid on forecasting Models
- Forecasting time series with missing values

Introduction¶
Deep Learning is a field of artificial intelligence focused on creating models based on neural networks that allow learning non-linear representations. Recurrent neural networks (RNN) are a type of deep learning architecture designed to work with sequential data, where information is propagated through recurrent connections, allowing the network to learn temporal dependencies.
This article describes how to train recurrent neural network models, specifically RNN, GRU and LSTM, for time series prediction (forecasting) using Python, Keras and skforecast.
Keras3 provides a friendly interface to build and train neural network models. Thanks to its high-level API, developers can easily implement LSTM architectures, taking advantage of the computational efficiency and scalability offered by deep learning.
Skforecast eases the implementation and use of machine learning models to forecasting problems. Using this package, the user can define the problem and abstract from the architecture. For advanced users, skforecast also allows to execute a previously defined deep learning architecture.
✏️ Note
To fully understand this article, some knowledge about neural networks and deep learning is presupposed. However, if this is not the case, and while we work on creating new material, we provide you with some reference links to start:
Aditional use cases of skforecast with deep learning models are available in the following articles:Recurrent Neural Networks (RNN)¶
Recurrent Neural Networks (RNN) are a family of models specifically designed to work with sequential data, such as time series. Unlike traditional feedforward neural networks, which treat each input independently, RNNs introduce an internal memory that allows them to capture dependencies between elements of a sequence. This enables the model to leverage information from previous steps to improve future predictions.
The fundamental building block of an RNN is the recurrent cell, which receives two inputs at each time step: the current data point and the previous hidden state (the "memory" of the network). At every step, the hidden state is updated, storing relevant information about the sequence up to that point. This architecture allows RNNs to “remember” trends and patterns over time.
However, simple RNNs face difficulties when learning long-term dependencies due to issues like the vanishing or exploding gradient problem. To address these limitations, more advanced architectures such as Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) were developed. These variants are better at capturing complex and long-range patterns in time series data.
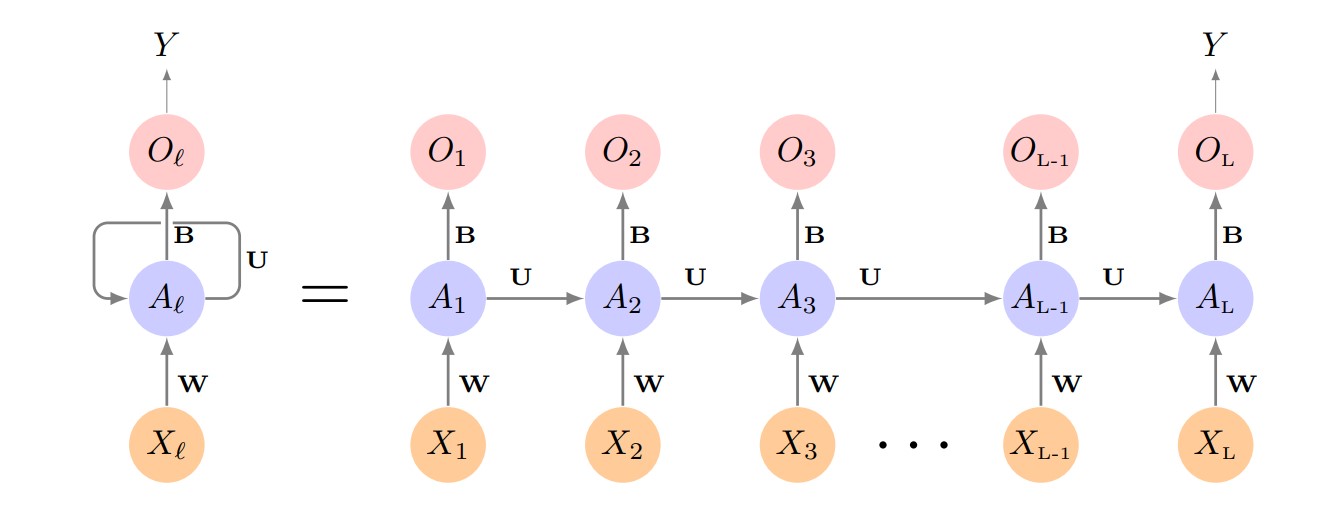
Basic RNN diagram. Source: James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An introduction to statistical learning (1st ed.) [PDF]. Springer.
Long Short-Term Memory (LSTM)¶
Long Short-Term Memory (LSTM) networks are a widely used type of recurrent neural network designed to effectively capture long-range dependencies in sequential data. Unlike simple RNNs, LSTMs use a more sophisticated architecture based on a system of memory cells and gates that control the flow of information over time.
The core component of an LSTM is the memory cell, which maintains information across time steps. Three gates regulate how information is added, retained, or discarded at each step:
Forget Gate: Decides which information from the previous cell state should be removed. It uses the current input and previous hidden state, applying a sigmoid activation to produce a value between 0 and 1 (where 0 means “completely forget” and 1 means “completely keep”).
Input Gate: Controls how much new information is added to the cell state, again using the current input and previous hidden state with a sigmoid activation.
Output Gate: Determines how much of the cell state is exposed as output and passed to the next hidden state.
This gating mechanism enables LSTMs to selectively remember or forget information, making them highly effective for modeling sequences with long-term patterns.
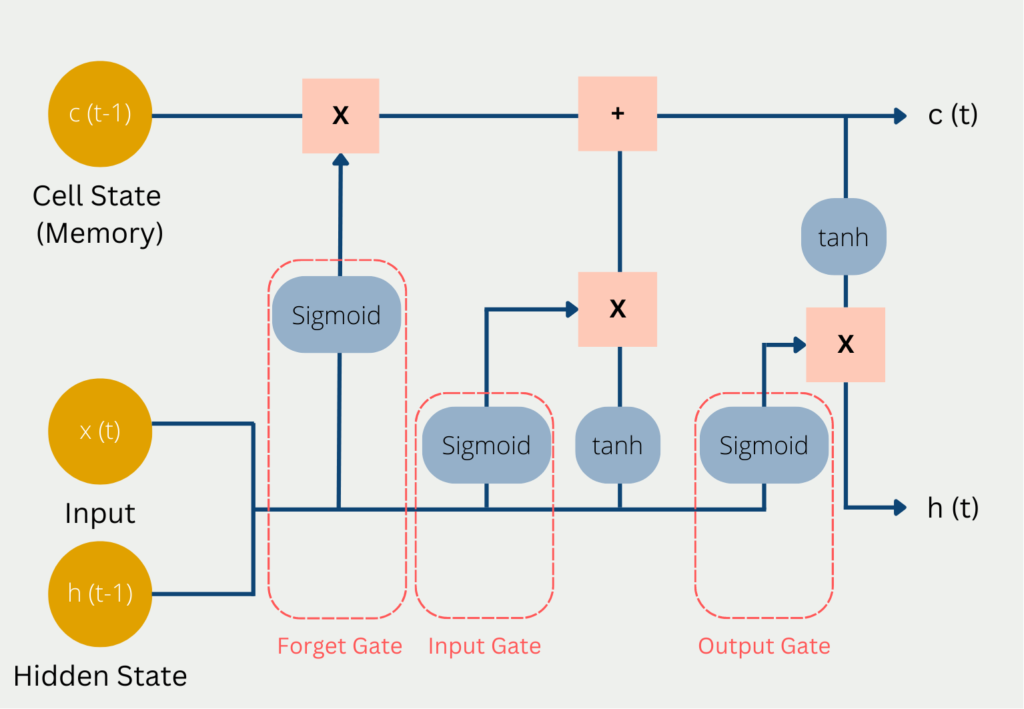
Diagram of the inputs and outputs of an LSTM. Source: codificandobits https://databasecamp.de/wp-content/uploads/lstm-architecture-1024x709.png.
Gated Recurrent Unit (GRU) cells are a simplified alternative to LSTMs, using only two gates (reset and update) but often achieving similar performance. GRUs require fewer parameters and can be computationally more efficient, which may be an advantage for some tasks or larger datasets.
Types of Recurrent Layers in skforecast¶
With skforecast, you can use three main types of recurrent cells:
Simple RNN: Suitable for problems with short-term dependencies or when a simple model is sufficient. Less effective for capturing long-range patterns.
LSTM (Long Short-Term Memory): Adds gating mechanisms that allow the network to learn and retain information over longer periods. LSTMs are a popular choice for many complex forecasting problems.
GRU (Gated Recurrent Unit): Offers a simpler structure than LSTM, using fewer parameters while achieving comparable performance in many scenarios. Useful when computational efficiency is important.
✏️ Note
Guidelines for choosing a recurrent layer:
- Use LSTM if your time series contains long-term patterns or complex dependencies.
- Try GRU as a lighter alternative to LSTM.
- Use Simple RNN only for straightforward tasks or as a baseline.
Types of problems in time series forecasting¶
The complexity of a forecasting problem is usually determined by three key questions:
Which series will be used to train the model?
Which series (and how many) are you trying to predict?
How many steps into the future do you want to forecast?
These decisions shape the structure of your dataset and the design of your forecasting model, and are essential when tackling time series problems.
Deep learning models for time series can handle a wide variety of forecasting scenarios, depending on how you structure your input data and define your prediction targets. These models can represent the following scenarios:
1:1 Problems — Single-series, single-output
- Description: The model uses only the past values of one series to predict its own future values. This is the classic autoregressive setup.
- Example: Predicting tomorrow’s temperature using only previous temperature measurements.
N:1 Problems — Multi-series, single-output
- Description: The model uses several series as predictors, but the target is just one series. Each predictor can be a different variable or entity, but the goal is to forecast only one outcome.
- Example: Predicting tomorrow’s temperature using temperature, humidity, and atmospheric pressure series.
N:M Problems — Multi-series, multi-output
- Description: The model uses multiple series as predictors and forecasts multiple target series simultaneously.
- Example: Forecasting the future prices of several stocks based on historical data of many stocks, energy prices, and commodity prices.
All of these scenarios can be framed as either single-step forecasting (predicting only the next time point) or multi-step forecasting (predicting several time points ahead).
You can further enhance your models by incorporating exogenous variables, external features or additional information known in advance (such as calendar effects, promotions, or weather forecasts), alongside your main time series data.
Defining the right deep learning architecture for each case can be challenging. The skforecast library helps by automatically selecting the appropriate architecture for each scenario, making the modeling process much easier and faster.
Below, you’ll find examples of how to use skforecast to solve each of these time series problems using recurrent neural networks.
Data¶
The data used in this article contains detailed information on air quality in the city of Valencia (Spain). The data collection spans from January 1, 2019 to December 31, 2021, providing hourly measurements of various air pollutants, such as PM2.5 and PM10 particles, carbon monoxide (CO), nitrogen dioxide (NO2), among others. The data has been obtained from the *Red de Vigilancia y Control de la Contaminación Atmosférica, 46250054-València - Centre, https://mediambient.gva.es/es/web/calidad-ambiental/datos-historicos platform.
Libraries¶
⚠️ Warning
skforecast supports multiple Keras backends: TensorFlow, JAX, and PyTorch (torch).
You can select the backend using the KERAS_BACKEND environment variable, or by editing your local configuration file at ~/.keras/keras.json.
```python
import os
os.environ["KERAS_BACKEND"] = "torch" # Options: "tensorflow", "jax", or "torch"
import keras
```
The backend must be set before importing Keras in your Python session. Once Keras is imported, the backend cannot be changed without restarting your Python process.
Alternatively, you can set the backend in your configuration file at ~/.keras/keras.json:
```json
{
"backend": "torch" # Options: "tensorflow", "jax", or "torch"
}
```
# Data processing
# ==============================================================================
import os
import numpy as np
import pandas as pd
# Plotting
# ==============================================================================
import matplotlib.pyplot as plt
import plotly.graph_objects as go
import plotly.io as pio
import plotly.offline as poff
pio.templates.default = "seaborn"
poff.init_notebook_mode(connected=True)
# Keras
# ==============================================================================
os.environ["KERAS_BACKEND"] = "torch" # 'tensorflow', 'jax´ or 'torch'
import keras
from keras.optimizers import Adam
from keras.losses import MeanSquaredError
from keras.callbacks import EarlyStopping, ReduceLROnPlateau
# Feature engineering
# ==============================================================================
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import make_pipeline
from feature_engine.datetime import DatetimeFeatures
from feature_engine.creation import CyclicalFeatures
# Time series modeling
# ==============================================================================
import skforecast
from skforecast.plot import set_dark_theme
from skforecast.datasets import fetch_dataset
from skforecast.deep_learning import ForecasterRnn
from skforecast.deep_learning import create_and_compile_model
from skforecast.model_selection import TimeSeriesFold
from skforecast.model_selection import backtesting_forecaster_multiseries
from skforecast.plot import plot_prediction_intervals
# Warning configuration
# ==============================================================================
import warnings
warnings.filterwarnings('ignore', category=DeprecationWarning)
color = '\033[1m\033[38;5;208m'
print(f"{color}skforecast version: {skforecast.__version__}")
print(f"{color}Keras version: {keras.__version__}")
print(f"{color}Using backend: {keras.backend.backend()}")
if keras.backend.backend() == "tensorflow":
import tensorflow as tf
print(f"{color}tensorflow version: {tf.__version__}")
elif keras.backend.backend() == "torch":
import torch
print(f"{color}torch version: {torch.__version__}")
print(" Cuda available :", torch.cuda.is_available())
print(" Device name :", torch.cuda.get_device_name(0) if torch.cuda.is_available() else "CPU")
else:
print(f"{color}Backend not recognized. Please use 'tensorflow' or 'torch'.")
skforecast version: 0.19.0 Keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126 Cuda available : True Device name : Tesla T4
# Downloading the dataset and processing it
# ==============================================================================
data = fetch_dataset(name="air_quality_valencia_no_missing")
data.head()
╭──────────────────────── air_quality_valencia_no_missing ─────────────────────────╮ │ Description: │ │ Hourly measures of several air chemical pollutant at Valencia city (Avd. │ │ Francia) from 2019-01-01 to 20213-12-31. Including the following variables: │ │ pm2.5 (µg/m³), CO (mg/m³), NO (µg/m³), NO2 (µg/m³), PM10 (µg/m³), NOx (µg/m³), │ │ O3 (µg/m³), Veloc. (m/s), Direc. (degrees), SO2 (µg/m³). Missing values have │ │ been imputed using linear interpolation. │ │ │ │ Source: │ │ Red de Vigilancia y Control de la Contaminación Atmosférica, 46250047-València - │ │ Av. França, https://mediambient.gva.es/es/web/calidad-ambiental/datos- │ │ historicos. │ │ │ │ URL: │ │ https://raw.githubusercontent.com/skforecast/skforecast- │ │ datasets/main/data/air_quality_valencia_no_missing.csv │ │ │ │ Shape: 43824 rows x 10 columns │ ╰──────────────────────────────────────────────────────────────────────────────────╯
| so2 | co | no | no2 | pm10 | nox | o3 | veloc. | direc. | pm2.5 | |
|---|---|---|---|---|---|---|---|---|---|---|
| datetime | ||||||||||
| 2019-01-01 00:00:00 | 8.0 | 0.2 | 3.0 | 36.0 | 22.0 | 40.0 | 16.0 | 0.5 | 262.0 | 19.0 |
| 2019-01-01 01:00:00 | 8.0 | 0.1 | 2.0 | 40.0 | 32.0 | 44.0 | 6.0 | 0.6 | 248.0 | 26.0 |
| 2019-01-01 02:00:00 | 8.0 | 0.1 | 11.0 | 42.0 | 36.0 | 58.0 | 3.0 | 0.3 | 224.0 | 31.0 |
| 2019-01-01 03:00:00 | 10.0 | 0.1 | 15.0 | 41.0 | 35.0 | 63.0 | 3.0 | 0.2 | 220.0 | 30.0 |
| 2019-01-01 04:00:00 | 11.0 | 0.1 | 16.0 | 39.0 | 36.0 | 63.0 | 3.0 | 0.4 | 221.0 | 30.0 |
It is verified that the data set has an index of type DatetimeIndex with hourly frequency.
# Checking the frequency of the time series
# ==============================================================================
print(f"Index : {data.index.dtype}")
print(f"Frequency : {data.index.freqstr}")
Index : datetime64[ns] Frequency : h
To facilitate the training of the models and the evaluation of their predictive capacity, the data is divided into three separate sets: training, validation, and test.
# Split train-validation-test
# ==============================================================================
data = data.loc["2019-01-01 00:00:00":"2021-12-31 23:59:59", :].copy()
end_train = "2021-03-31 23:59:00"
end_validation = "2021-09-30 23:59:00"
data_train = data.loc[:end_train, :].copy()
data_val = data.loc[end_train:end_validation, :].copy()
data_test = data.loc[end_validation:, :].copy()
print(
f"Dates train : {data_train.index.min()} --- "
f"{data_train.index.max()} (n={len(data_train)})"
)
print(
f"Dates validation : {data_val.index.min()} --- "
f"{data_val.index.max()} (n={len(data_val)})"
)
print(
f"Dates test : {data_test.index.min()} --- "
f"{data_test.index.max()} (n={len(data_test)})"
)
Dates train : 2019-01-01 00:00:00 --- 2021-03-31 23:00:00 (n=19704) Dates validation : 2021-04-01 00:00:00 --- 2021-09-30 23:00:00 (n=4392) Dates test : 2021-10-01 00:00:00 --- 2021-12-31 23:00:00 (n=2208)
# Plot series
# ==============================================================================
set_dark_theme()
colors = plt.rcParams['axes.prop_cycle'].by_key()['color'] * 2
fig, axes = plt.subplots(len(data.columns), 1, figsize=(8, 8), sharex=True)
for i, col in enumerate(data.columns):
axes[i].plot(data[col], label=col, color=colors[i])
axes[i].legend(loc='upper right', fontsize=8)
axes[i].tick_params(axis='both', labelsize=8)
axes[i].axvline(pd.to_datetime(end_train), color='white', linestyle='--', linewidth=1) # End train
axes[i].axvline(pd.to_datetime(end_validation), color='white', linestyle='--', linewidth=1) # End validation
fig.suptitle("Air Quality Valencia", fontsize=16)
plt.tight_layout()
Building RNN-based models easily with create_and_compile_model¶
skforecast provides the utility function create_and_compile_model to simplify the creation of recurrent neural network architectures (RNN, LSTM, or GRU) for time series forecasting. This function is designed to make it easy for both beginners and advanced users to build and compile Keras models with just a few lines of code.
Basic usage
For most forecasting scenarios, you can simply specify the time series data, the number of lagged observations, the number of steps to predict, and the type of recurrent layer you wish to use (LSTM, GRU, or SimpleRNN). By default, the function sets reasonable parameters for each layer, but all architectural details can be adjusted to fit specific requirements.
# Basic usage of `create_and_compile_model`
# ==============================================================================
model = create_and_compile_model(
series = data, # All 10 series are used as predictors
levels = ["o3"], # Target series to predict
lags = 32, # Number of lags to use as predictors
steps = 24, # Number of steps to predict
recurrent_layer = "LSTM", # Type of recurrent layer ('LSTM', 'GRU', or 'RNN')
recurrent_units = 100, # Number of units in the recurrent layer
dense_units = 64 # Number of units in the dense layer
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "functional"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 32, 10) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ lstm_1 (LSTM) │ (None, 100) │ 44,400 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 64) │ 6,464 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 24) │ 1,560 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 24, 1) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 52,424 (204.78 KB)
Trainable params: 52,424 (204.78 KB)
Non-trainable params: 0 (0.00 B)
Advanced customization
All arguments controlling layer types, units, activations, and other options can be customized. You may also pass your own Keras model if you need full flexibility beyond what the helper function provides.
The arguments recurrent_layers_kwargs and dense_layers_kwargs allow you to specify the parameters for the recurrent and dense layers, respectively.
When using a dictionary, the kwargs are replayed for each layer of the same type. For example, if you specify
recurrent_layers_kwargs = {'activation': 'tanh'}, all recurrent layers will use thetanhactivation function.You can also pass a list of dictionaries to specify different parameters for each layer. For instance,
recurrent_layers_kwargs = [{'activation': 'tanh'}, {'activation': 'relu'}]will specify that the first recurrent layer uses thetanhactivation function and the second usesrelu.
# Advance usage of `create_and_compile_model`
# ==============================================================================
model = create_and_compile_model(
series = data,
levels = ["o3"],
lags = 32,
steps = 24,
exog = None, # No exogenous variables
recurrent_layer = "LSTM",
recurrent_units = [128, 64],
recurrent_layers_kwargs = [{'activation': 'tanh'}, {'activation': 'relu'}],
dense_units = [128, 64],
dense_layers_kwargs = {'activation': 'relu'},
output_dense_layer_kwargs = {'activation': 'linear'},
compile_kwargs = {'optimizer': Adam(learning_rate=0.001), 'loss': MeanSquaredError()},
model_name = None
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "functional_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 32, 10) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ lstm_1 (LSTM) │ (None, 32, 128) │ 71,168 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ lstm_2 (LSTM) │ (None, 64) │ 49,408 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 128) │ 8,320 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_2 (Dense) │ (None, 64) │ 8,256 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 24) │ 1,560 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 24, 1) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 138,712 (541.84 KB)
Trainable params: 138,712 (541.84 KB)
Non-trainable params: 0 (0.00 B)
To gain a deeper understanding of this function, refer to a later section of this guide: Understanding create_and_compile_model in depth.
If you need to define a completely custom architecture, you can create your own Keras model and use it directly in skforecast workflows.
# Plotting the model architecture (require `pydot` and `graphviz`)
# ==============================================================================
# from keras.utils import plot_model
# plot_model(model, show_shapes=True, show_layer_names=True, to_file='model-architecture.png')

Once the model has been created and compiled, the next step is to create an instance of ForecasterRnn. This class is responsible for adding to the deep learning model all the functionalities necessary to be used in forecasting problems. It is also compatible with the rest of the functionalities offered by skforecast (backtesting, exogenous variables, ...).
1:1 Problems — Single-series, single-output¶
In this scenario, the goal is to predict the next value in a single time series, using only its own past observations as predictors. This is known as a univariate autoregressive forecasting problem.
For example: Given a sequence of values ${y_{t-3}, y_{t-2}, y_{t-1}}$, predict $y_{t+1}$.
Single-step forecasting¶
This is the simplest scenario for forecasting with recurrent neural networks: both training and prediction are based on a single time series. In this case, you simply pass that series to the series argument of the create_and_compile_model function, and set the same series as the target using the levels argument. Since you want to predict only one value in the future, set the steps parameter to 1.
# Create model
# ==============================================================================
lags = 24
model = create_and_compile_model(
series = data[["o3"]], # Only the 'o3' series is used as predictor
levels = ["o3"], # Target series to predict
lags = lags, # Number of lags to use as predictors
steps = 1, # Single-step forecasting
recurrent_layer = "GRU",
recurrent_units = 64,
recurrent_layers_kwargs = {"activation": "tanh"},
dense_units = 32,
compile_kwargs = {'optimizer': Adam(), 'loss': MeanSquaredError()},
model_name = "Single-Series-Single-Step"
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "Single-Series-Single-Step"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 24, 1) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ gru_1 (GRU) │ (None, 64) │ 12,864 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 32) │ 2,080 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 1) │ 33 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 1, 1) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 14,977 (58.50 KB)
Trainable params: 14,977 (58.50 KB)
Non-trainable params: 0 (0.00 B)
The forecaster is created using the model, and validation data is provided so that the model’s performance can be evaluated at each epoch. A MinMaxScaler is also used to standardize the input and output data. This scaler handles scaling for both training and predictions, ensuring results are brought back to their original scale.
The fit_kwargs dictionary contains the parameters passed to the model’s fit method. In this example, it specifies the number of training epochs, batch size, validation data, and an EarlyStopping callback, which stops training if the validation loss does not improve.
# Forecaster Creation
# ==============================================================================
forecaster = ForecasterRnn(
estimator=model,
levels=["o3"],
lags=lags, # Must be same lags as used in create_and_compile_model
transformer_series=MinMaxScaler(),
fit_kwargs={
"epochs": 25, # Number of epochs to train the model.
"batch_size": 512, # Batch size to train the model.
"callbacks": [
EarlyStopping(monitor="val_loss", patience=3, restore_best_weights=True)
], # Callback to stop training when it is no longer learning.
"series_val": data_val, # Validation data for model training.
},
)
# Fit forecaster
# ==============================================================================
forecaster.fit(data_train[['o3']])
forecaster
Using 'torch' backend with device: cuda Epoch 1/25
39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0879 - val_loss: 0.0122 Epoch 2/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 54ms/step - loss: 0.0121 - val_loss: 0.0088 Epoch 3/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 52ms/step - loss: 0.0084 - val_loss: 0.0071 Epoch 4/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0070 - val_loss: 0.0061 Epoch 5/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 45ms/step - loss: 0.0062 - val_loss: 0.0058 Epoch 6/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0059 - val_loss: 0.0060 Epoch 7/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 45ms/step - loss: 0.0055 - val_loss: 0.0054 Epoch 8/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0054 - val_loss: 0.0056 Epoch 9/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 58ms/step - loss: 0.0054 - val_loss: 0.0058 Epoch 10/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 45ms/step - loss: 0.0053 - val_loss: 0.0054 Epoch 11/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 45ms/step - loss: 0.0053 - val_loss: 0.0053 Epoch 12/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 45ms/step - loss: 0.0053 - val_loss: 0.0053 Epoch 13/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0053 - val_loss: 0.0052 Epoch 14/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0050 - val_loss: 0.0054 Epoch 15/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 58ms/step - loss: 0.0051 - val_loss: 0.0051 Epoch 16/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 48ms/step - loss: 0.0052 - val_loss: 0.0055 Epoch 17/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0049 - val_loss: 0.0058 Epoch 18/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0052 - val_loss: 0.0050 Epoch 19/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0049 - val_loss: 0.0054 Epoch 20/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0050 - val_loss: 0.0054 Epoch 21/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 52ms/step - loss: 0.0049 - val_loss: 0.0050 Epoch 22/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 53ms/step - loss: 0.0050 - val_loss: 0.0049 Epoch 23/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 45ms/step - loss: 0.0050 - val_loss: 0.0049 Epoch 24/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0048 - val_loss: 0.0049 Epoch 25/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 54ms/step - loss: 0.0048 - val_loss: 0.0049
ForecasterRnn
General Information
- Estimator: Functional
- Layers names: ['series_input', 'gru_1', 'dense_1', 'output_dense_td_layer', 'reshape']
- Lags: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]
- Window size: 24
- Maximum steps to predict: [1]
- Exogenous included: False
- Creation date: 2025-11-27 11:31:45
- Last fit date: 2025-11-27 11:32:33
- Keras backend: torch
- Skforecast version: 0.19.0
- Python version: 3.12.12
- Forecaster id: None
Exogenous Variables
-
None
Data Transformations
- Transformer for series: MinMaxScaler()
- Transformer for exog: MinMaxScaler()
Training Information
- Series names: o3
- Target series (levels): ['o3']
- Training range: [Timestamp('2019-01-01 00:00:00'), Timestamp('2021-03-31 23:00:00')]
- Training index type: DatetimeIndex
- Training index frequency:
Estimator Parameters
-
{'name': 'Single-Series-Single-Step', 'trainable': True, 'layers': [{'module': 'keras.layers', 'class_name': 'InputLayer', 'config': {'batch_shape': (None, 24, 1), 'dtype': 'float32', 'sparse': False, 'ragged': False, 'name': 'series_input'}, 'registered_name': None, 'name': 'series_input', 'inbound_nodes': []}, {'module': 'keras.layers', 'class_name': 'GRU', 'config': {'name': 'gru_1', 'trainable': True, 'dtype': {'module': 'keras', 'class_name': 'DTypePolicy', 'config': {'name': 'float32'}, 'registered_name': None}, 'return_sequences': False, 'return_state': False, 'go_backwards': False, 'stateful': False, 'unroll': False, 'zero_output_for_mask': False, 'units': 64, 'activation': 'tanh', 'recurrent_activation': 'sigmoid', 'use_bias': True, 'kernel_initializer': {'module': 'keras.initializers', 'class_name': 'GlorotUniform', 'config': {'seed': None}, 'registered_name': None}, 'recurrent_initializer': {'module': 'keras.initializers', 'class_name': 'Orthogonal', 'config': {'seed': None, 'gain': 1.0}, 'registered_name': None}, 'bias_initializer': {'module': 'keras.initializers', 'class_name': 'Zeros', 'config': {}, 'registered_name': None}, 'kernel_regularizer': None, 'recurrent_regularizer': None, 'bias_regularizer': None, 'activity_regularizer': None, 'kernel_constraint': None, 'recurrent_constraint': None, 'bias_constraint': None, 'dropout': 0.0, 'recurrent_dropout': 0.0, 'reset_after': True, 'seed': None}, 'registered_name': None, 'build_config': {'input_shape': [None, 24, 1]}, 'name': 'gru_1', 'inbound_nodes': [{'args': ({'class_name': '__keras_tensor__', 'config': {'shape': (None, 24, 1), 'dtype': 'float32', 'keras_history': ['series_input', 0, 0]}},), 'kwargs': {'training': False, 'mask': None}}]}, {'module': 'keras.layers', 'class_name': 'Dense', 'config': {'name': 'dense_1', 'trainable': True, 'dtype': {'module': 'keras', 'class_name': 'DTypePolicy', 'config': {'name': 'float32'}, 'registered_name': None}, 'units': 32, 'activation': 'relu', 'use_bias': True, 'kernel_initializer': {'module': 'keras.initializers', 'class_name': 'GlorotUniform', 'config': {'seed': None}, 'registered_name': None}, 'bias_initializer': {'module': 'keras.initializers', 'class_name': 'Zeros', 'config': {}, 'registered_name': None}, 'kernel_regularizer': None, 'bias_regularizer': None, 'kernel_constraint': None, 'bias_constraint': None}, 'registered_name': None, 'build_config': {'input_shape': [None, 64]}, 'name': 'dense_1', 'inbound_nodes': [{'args': ({'class_name': '__keras_tensor__', 'config': {'shape': (None, 64), 'dtype': 'float32', 'keras_history': ['gru_1', 0, 0]}},), 'kwargs': {}}]}, {'module': 'keras.layers', 'class_name': 'Dense', 'config': {'name': 'output_dense_td_layer', 'trainable': True, 'dtype': {'module': 'keras', 'class_name': 'DTypePolicy', 'config': {'name': 'float32'}, 'registered_name': None}, 'units': 1, 'activation': 'linear', 'use_bias': True, 'kernel_initializer': {'module': 'keras.initializers', 'class_name': 'GlorotUniform', 'config': {'seed': None}, 'registered_name': None}, 'bias_initializer': {'module': 'keras.initializers', 'class_name': 'Zeros', 'config': {}, 'registered_name': None}, 'kernel_regularizer': None, 'bias_regularizer': None, 'kernel_constraint': None, 'bias_constraint': None}, 'registered_name': None, 'build_config': {'input_shape': [None, 32]}, 'name': 'output_dense_td_layer', 'inbound_nodes': [{'args': ({'class_name': '__keras_tensor__', 'config': {'shape': (None, 32), 'dtype': 'float32', 'keras_history': ['dense_1', 0, 0]}},), 'kwargs': {}}]}, {'module': 'keras.layers', 'class_name': 'Reshape', 'config': {'name': 'reshape', 'trainable': True, 'dtype': {'module': 'keras', 'class_name': 'DTypePolicy', 'config': {'name': 'float32'}, 'registered_name': None}, 'target_shape': (1, 1)}, 'registered_name': None, 'build_config': {'input_shape': [None, 1]}, 'name': 'reshape', 'inbound_nodes': [{'args': ({'class_name': '__keras_tensor__', 'config': {'shape': (None, 1), 'dtype': 'float32', 'keras_history': ['output_dense_td_layer', 0, 0]}},), 'kwargs': {}}]}], 'input_layers': [['series_input', 0, 0]], 'output_layers': [['reshape', 0, 0]]}
Compile Parameters
-
{'optimizer': {'module': 'keras.src.backend.torch.optimizers.torch_adam', 'class_name': 'Adam', 'config': {'name': 'adam', 'learning_rate': 0.0010000000474974513, 'weight_decay': None, 'clipnorm': None, 'global_clipnorm': None, 'clipvalue': None, 'use_ema': False, 'ema_momentum': 0.99, 'ema_overwrite_frequency': None, 'loss_scale_factor': None, 'gradient_accumulation_steps': None, 'beta_1': 0.9, 'beta_2': 0.999, 'epsilon': 1e-07, 'amsgrad': False}, 'registered_name': 'Adam'}, 'loss': {'module': 'keras.losses', 'class_name': 'MeanSquaredError', 'config': {'name': 'mean_squared_error', 'reduction': 'sum_over_batch_size'}, 'registered_name': None}, 'loss_weights': None, 'metrics': None, 'weighted_metrics': None, 'run_eagerly': False, 'steps_per_execution': 1, 'jit_compile': False}
Fit Kwargs
-
{'epochs': 25, 'batch_size': 512, 'callbacks': [
✏️ Note
The skforecast library is fully compatible with GPUs. See the Running on GPU section below in this document for more information.
In deep learning models, it’s important to control overfitting, when a model performs well on training data but poorly on new, unseen data. One common approach is to use a Keras callback, such as EarlyStopping, which halts training if the validation loss stops improving.
Another useful practice is to plot the training and validation loss after each epoch. This helps you visualize how the model is learning and spot signs of overfitting.

Graphical explanation of overfitting. Source: https://datahacker.rs/018-pytorch-popular-techniques-to-prevent-the-overfitting-in-a-neural-networks/.
# Track training and overfitting
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 3))
_ = forecaster.plot_history(ax=ax)
In the plot above, the training loss (blue) decreases rapidly during the first two epochs, indicating the model is quickly capturing the main patterns in the data. The validation loss (red) starts low and remains stable throughout the training process, closely following the training loss. This suggests:
The model is not overfitting, as the validation loss stays close to the training loss for all epochs.
Both losses decrease and stabilize together, indicating good generalization and effective learning.
No divergence is observed, which would appear as the validation loss increasing while training loss keeps decreasing.
When the magnitude of the loss function is very different between training and validation, it is recommended to plot the training and validation values using different axes and scales. This approach allows for a clearer visualization of the loss trends, making it easier to identify issues of overfitting or underfitting in the model.
# Track training and overfitting with different axes and scales
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 3))
epochs = np.arange(len(forecaster.history_['loss']))
p1, = ax.plot(epochs, forecaster.history_['loss'], color='tab:blue', label='loss')
ax.set_ylabel('loss', color='tab:blue')
ax.tick_params(axis='y', labelcolor='tab:blue')
ax2 = ax.twinx()
p2, = ax2.plot(epochs, forecaster.history_['val_loss'], color='tab:orange', label='val_loss')
ax2.set_ylabel('val_loss', color='tab:orange')
ax2.tick_params(axis='y', labelcolor='tab:orange')
ax.legend(handles=[p1, p2], loc='upper right')
ax.set_title('Training and Validation Loss over Epochs')
plt.show()
Once the forecaster has been trained, predictions can be obtained. If the steps parameter is set to None in the predict method, the forecaster will predict all available steps, forecaster.max_step.
# Forecaster available steps
# ==============================================================================
forecaster.max_step
np.int64(1)
# Predictions
# ==============================================================================
predictions = forecaster.predict(steps=None) # Same as steps=1
predictions
| level | pred | |
|---|---|---|
| 2021-04-01 | o3 | 44.045647 |
In time series forecasting, the process of backtesting consists of evaluating the performance of a predictive model by applying it retrospectively to historical data. Therefore, it is a special type of cross-validation applied to the previous period(s). To learn more about backtesting, visit the backtesting user guide.
✏️ Note
In the previous step, the validation partition was used to check that the model learns and to identify the number of epochs with which the best performance is achieved. In the next step (backtesting), the validation partition is included in the training set to take advantage of all available data before evaluating the model on the test set. The forecaster.set_fit_kwargs() method is used to update the model fitting arguments before the backtesting it.
# Backtesting with test data
# ==============================================================================
cv = TimeSeriesFold(
steps = forecaster.max_step,
initial_train_size = len(data.loc[:end_validation, :]), # Training + Validation Data
refit = False
)
# The validation partition is now used as part of the initial fit
# Epocs is set to the value idenfied in the previous training with early stopping
forecaster.set_fit_kwargs({"epochs": 25,"batch_size": 512})
metrics, predictions = backtesting_forecaster_multiseries(
forecaster = forecaster,
series = data[['o3']],
cv = cv,
levels = forecaster.levels,
metric = "mean_absolute_error",
verbose = False # Set to True for detailed output
)
Using 'torch' backend with device: cuda Epoch 1/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 49ms/step - loss: 0.0051 Epoch 2/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0056 Epoch 3/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0049 Epoch 4/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0050 Epoch 5/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0049 Epoch 6/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0048 Epoch 7/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 52ms/step - loss: 0.0048 Epoch 8/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0047 Epoch 9/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0052 Epoch 10/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0047 Epoch 11/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0049 Epoch 12/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0048 Epoch 13/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 3s 52ms/step - loss: 0.0046 Epoch 14/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0049 Epoch 15/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0047 Epoch 16/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0046 Epoch 17/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0047 Epoch 18/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 43ms/step - loss: 0.0051 Epoch 19/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 48ms/step - loss: 0.0048 Epoch 20/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0049 Epoch 21/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0051 Epoch 22/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0048 Epoch 23/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0047 Epoch 24/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 45ms/step - loss: 0.0048 Epoch 25/25 48/48 ━━━━━━━━━━━━━━━━━━━━ 2s 48ms/step - loss: 0.0051
0%| | 0/2208 [00:00<?, ?it/s]
# Backtesting metrics
# ==============================================================================
metrics
| levels | mean_absolute_error | |
|---|---|---|
| 0 | o3 | 7.68559 |
# Backtesting predictions
# ==============================================================================
predictions.head(4)
| level | fold | pred | |
|---|---|---|---|
| 2021-10-01 00:00:00 | o3 | 0 | 46.797310 |
| 2021-10-01 01:00:00 | o3 | 1 | 50.834579 |
| 2021-10-01 02:00:00 | o3 | 2 | 54.101501 |
| 2021-10-01 03:00:00 | o3 | 3 | 54.018898 |
# Plotting predictions vs real values in the test set
# ==============================================================================
fig = go.Figure()
trace1 = go.Scatter(x=data_test.index, y=data_test['o3'], name="test", mode="lines")
trace2 = go.Scatter(
x=predictions.index,
y=predictions.loc[predictions["level"] == "o3", "pred"],
name="predictions", mode="lines"
)
fig.add_trace(trace1)
fig.add_trace(trace2)
fig.update_layout(
title="Prediction vs real values in the test set",
xaxis_title="Date time",
yaxis_title="O3",
width=800,
height=400,
margin=dict(l=20, r=20, t=35, b=20),
legend=dict(orientation="h", yanchor="top", y=1.05, xanchor="left", x=0)
)
fig.show()
# % Error vs series mean
# ==============================================================================
rel_mse = 100 * metrics.loc[0, 'mean_absolute_error'] / np.mean(data["o3"])
print(f"Serie mean: {np.mean(data['o3']):0.2f}")
print(f"Relative error (mae): {rel_mse:0.2f} %")
Serie mean: 54.52 Relative error (mae): 14.10 %
Multi-step forecasting¶
In this scenario, the objective is to predict multiple future values of a single time series using only its own past observations as predictors. This is known as multi-step univariate forecasting.
For example: Given a sequence of values ${y_{t-24}, ..., y_{t-1}}$, predict ${y_{t+1}, y_{t+2}, ..., y_{t+n}}$, where $n$ is the prediction horizon (number of steps ahead).
This setup is common when you want to forecast several periods into the future (e.g., the next 24 hours of ozone concentration).
Model Architecture
You can use a similar network architecture as in the single-step case, but predicting multiple steps ahead usually benefits from increasing the capacity of the model (e.g., more units in LSTM/GRU layers or additional dense layers). This allows the model to better capture the complexity of forecasting several points at once.
# Create model
# ==============================================================================
lags = 24
model = create_and_compile_model(
series = data[["o3"]], # Only the 'o3' series is used as predictor
levels = ["o3"], # Target series to predict
lags = lags, # Number of lags to use as predictors
steps = 24, # Multi-step forecasting
recurrent_layer = "GRU",
recurrent_units = 128,
recurrent_layers_kwargs = {"activation": "tanh"},
dense_units = 64,
compile_kwargs = {'optimizer': 'adam', 'loss': 'mse'},
model_name = "Single-Series-Multi-Step"
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "Single-Series-Multi-Step"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 24, 1) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ gru_1 (GRU) │ (None, 128) │ 50,304 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 64) │ 8,256 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 24) │ 1,560 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 24, 1) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 60,120 (234.84 KB)
Trainable params: 60,120 (234.84 KB)
Non-trainable params: 0 (0.00 B)
✏️ Note
The fit_kwargs parameter lets you customize any aspect of the model training process, passing arguments directly to the underlying Keras Model.fit() method. For example, you can specify the number of training epochs, batch size, and any callbacks you want to use.
In the code example, the model is trained for 50 epochs with a batch size of 512. The EarlyStopping callback monitors the validation loss and automatically stops training if it does not improve for 3 consecutive epochs (patience=3). This helps prevent overfitting and saves computation time.
You can also add other callbacks, such as ModelCheckpoint to save the model at each epoch, or TensorBoard for real-time visualization of training and validation metrics.
# Forecaster Creation
# ==============================================================================
forecaster = ForecasterRnn(
estimator=model,
levels=["o3"],
lags=lags,
transformer_series=MinMaxScaler(),
fit_kwargs={
"epochs": 25,
"batch_size": 512,
"callbacks": [
EarlyStopping(monitor="val_loss", patience=3, restore_best_weights=True)
], # Callback to stop training when it is no longer learning.
"series_val": data_val, # Validation data for model training.
},
)
# Fit forecaster
# ==============================================================================
forecaster.fit(data_train[['o3']])
Using 'torch' backend with device: cuda Epoch 1/25 1/39 ━━━━━━━━━━━━━━━━━━━━ 2s 64ms/step - loss: 0.1743
39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 57ms/step - loss: 0.1143 - val_loss: 0.0321 Epoch 2/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0292 - val_loss: 0.0270 Epoch 3/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0264 - val_loss: 0.0237 Epoch 4/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0247 - val_loss: 0.0220 Epoch 5/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0232 - val_loss: 0.0203 Epoch 6/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0214 - val_loss: 0.0180 Epoch 7/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 61ms/step - loss: 0.0204 - val_loss: 0.0177 Epoch 8/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 45ms/step - loss: 0.0200 - val_loss: 0.0174 Epoch 9/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 45ms/step - loss: 0.0197 - val_loss: 0.0174 Epoch 10/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0193 - val_loss: 0.0170 Epoch 11/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 45ms/step - loss: 0.0191 - val_loss: 0.0167 Epoch 12/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0188 - val_loss: 0.0171 Epoch 13/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 57ms/step - loss: 0.0186 - val_loss: 0.0166 Epoch 14/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 51ms/step - loss: 0.0184 - val_loss: 0.0166 Epoch 15/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 47ms/step - loss: 0.0182 - val_loss: 0.0163 Epoch 16/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 45ms/step - loss: 0.0181 - val_loss: 0.0164 Epoch 17/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 45ms/step - loss: 0.0179 - val_loss: 0.0166 Epoch 18/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 2s 46ms/step - loss: 0.0178 - val_loss: 0.0164
# Train and overfitting tracking
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3))
_ = forecaster.plot_history(ax=ax)
In this case, the prediction quality is expected to be lower than in the previous example, as shown by the higher loss values across epochs. This is easily explained: the model now has to predict 24 values at each step instead of just 1. As a result, the validation loss is higher, since it reflects the combined error across all 24 predicted values, rather than the error for a single value.
# Forecaster available steps
# ==============================================================================
forecaster.max_step
np.int64(24)
# Prediction
# ==============================================================================
predictions = forecaster.predict(steps=24) # Same as steps=None
predictions.head(4)
| level | pred | |
|---|---|---|
| 2021-04-01 00:00:00 | o3 | 51.077221 |
| 2021-04-01 01:00:00 | o3 | 49.373592 |
| 2021-04-01 02:00:00 | o3 | 43.191963 |
| 2021-04-01 03:00:00 | o3 | 38.597637 |
Specific steps can be predicted, as long as they are within the prediction horizon defined in the model.
# Specific step predictions
# ==============================================================================
predictions = forecaster.predict(steps=[1, 3])
predictions
| level | pred | |
|---|---|---|
| 2021-04-01 00:00:00 | o3 | 51.077221 |
| 2021-04-01 02:00:00 | o3 | 43.191963 |
# Backtesting
# ==============================================================================
cv = TimeSeriesFold(
steps = forecaster.max_step,
initial_train_size = len(data.loc[:end_validation, :]), # Training + Validation Data
refit = False
)
# The validation partition is now used as part of the initial fit
# Epocs is set to the value idenfied in the previous training with early stopping
forecaster.set_fit_kwargs({"epochs": 19,"batch_size": 512})
metrics, predictions = backtesting_forecaster_multiseries(
forecaster = forecaster,
series = data[['o3']],
cv = cv,
levels = forecaster.levels,
metric = "mean_absolute_error",
verbose = False,
suppress_warnings = True
)
Using 'torch' backend with device: cuda Epoch 1/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0177 Epoch 2/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0175 Epoch 3/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0175 Epoch 4/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0176 Epoch 5/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0174 Epoch 6/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 53ms/step - loss: 0.0173 Epoch 7/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0172 Epoch 8/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0173 Epoch 9/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0170 Epoch 10/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0170 Epoch 11/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 41ms/step - loss: 0.0171 Epoch 12/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 53ms/step - loss: 0.0171 Epoch 13/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0171 Epoch 14/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 48ms/step - loss: 0.0168 Epoch 15/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0169 Epoch 16/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0168 Epoch 17/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 42ms/step - loss: 0.0167 Epoch 18/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 51ms/step - loss: 0.0167 Epoch 19/19 47/47 ━━━━━━━━━━━━━━━━━━━━ 2s 40ms/step - loss: 0.0168
0%| | 0/92 [00:00<?, ?it/s]
# Backtesting metrics
# ==============================================================================
metric_single_series = metrics.loc[metrics["levels"] == "o3", "mean_absolute_error"].iat[0]
metrics
| levels | mean_absolute_error | |
|---|---|---|
| 0 | o3 | 11.011109 |
# Backtesting predictions
# ==============================================================================
predictions
| level | fold | pred | |
|---|---|---|---|
| 2021-10-01 00:00:00 | o3 | 0 | 56.246929 |
| 2021-10-01 01:00:00 | o3 | 0 | 57.154469 |
| 2021-10-01 02:00:00 | o3 | 0 | 52.387318 |
| 2021-10-01 03:00:00 | o3 | 0 | 50.637001 |
| 2021-10-01 04:00:00 | o3 | 0 | 47.500042 |
| ... | ... | ... | ... |
| 2021-12-31 19:00:00 | o3 | 91 | 17.650108 |
| 2021-12-31 20:00:00 | o3 | 91 | 17.268902 |
| 2021-12-31 21:00:00 | o3 | 91 | 19.600010 |
| 2021-12-31 22:00:00 | o3 | 91 | 23.375639 |
| 2021-12-31 23:00:00 | o3 | 91 | 28.089417 |
2208 rows × 3 columns
# Plotting predictions vs real values in the test set
# ==============================================================================
fig = go.Figure()
trace1 = go.Scatter(x=data_test.index, y=data_test['o3'], name="test", mode="lines")
trace2 = go.Scatter(
x=predictions.index,
y=predictions.loc[predictions["level"] == "o3", "pred"],
name="predictions", mode="lines"
)
fig.add_trace(trace1)
fig.add_trace(trace2)
fig.update_layout(
title="Prediction vs real values in the test set",
xaxis_title="Date time",
yaxis_title="O3",
width=800,
height=400,
margin=dict(l=20, r=20, t=35, b=20),
legend=dict(orientation="h", yanchor="top", y=1.05, xanchor="left", x=0)
)
fig.show()
# % Error vs series mean
# ==============================================================================
rel_mse = 100 * metrics.loc[0, 'mean_absolute_error'] / np.mean(data["o3"])
print(f"Serie mean: {np.mean(data['o3']):0.2f}")
print(f"Relative error (mae): {rel_mse:0.2f} %")
Serie mean: 54.52 Relative error (mae): 20.20 %
In this case, the prediction is worse than in the previous case. This is to be expected since the model has to predict 24 values instead of 1.
N:1 Problems — Multi-series, single-output¶
In this scenario, the goal is to predict future values of a single target time series by leveraging the past values of multiple related series as predictors. This is known as multivariate forecasting, where the model uses the historical data from several variables to improve the prediction of one specific series.
For example: Suppose you want to forecast ozone concentration (o3) for the next 24 hours. In addition to past o3 values, you may include other series—such as temperature, wind speed, or other pollutant concentrations—as predictors. The model will then use the combined information from all available series to make a more accurate forecast.
Model setup
To handle this type of problem, the neural network architecture becomes a bit more complex. An additional recurrent layer is used to process the information from multiple input series, and another dense (fully connected) layer further processes the output from the recurrent layer. With skforecast, building such a model is straightforward: simply pass a list of integers to the recurrent_units and dense_units arguments to add multiple recurrent and dense layers as needed.
# Create model
# ==============================================================================
lags = 24
model = create_and_compile_model(
series = data, # DataFrame with all series (predictors)
levels = ["o3"], # Target series to predict
lags = lags, # Number of lags to use as predictors
steps = 24, # Multi-step forecasting
recurrent_layer = "GRU",
recurrent_units = [128, 64],
recurrent_layers_kwargs = {"activation": "tanh"},
dense_units = [64, 32],
compile_kwargs = {'optimizer': 'adam', 'loss': 'mse'},
model_name = "MultiVariate-Multi-Step"
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "MultiVariate-Multi-Step"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 24, 10) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ gru_1 (GRU) │ (None, 24, 128) │ 53,760 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ gru_2 (GRU) │ (None, 64) │ 37,248 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 64) │ 4,160 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_2 (Dense) │ (None, 32) │ 2,080 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 24) │ 792 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 24, 1) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 98,040 (382.97 KB)
Trainable params: 98,040 (382.97 KB)
Non-trainable params: 0 (0.00 B)
# Forecaster Creation
# ==============================================================================
forecaster = ForecasterRnn(
estimator=model,
levels=["o3"],
lags=lags,
transformer_series=MinMaxScaler(),
fit_kwargs={
"epochs": 25,
"batch_size": 512,
"callbacks": [
EarlyStopping(monitor="val_loss", patience=3, restore_best_weights=True)
], # Callback to stop training when it is no longer learning.
"series_val": data_val, # Validation data for model training.
},
)
# Fit forecaster
# ==============================================================================
forecaster.fit(data_train)
Using 'torch' backend with device: cuda Epoch 1/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 89ms/step - loss: 0.1398 - val_loss: 0.0637 Epoch 2/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 89ms/step - loss: 0.0419 - val_loss: 0.0262 Epoch 3/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 102ms/step - loss: 0.0264 - val_loss: 0.0244 Epoch 4/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 88ms/step - loss: 0.0245 - val_loss: 0.0226 Epoch 5/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 90ms/step - loss: 0.0231 - val_loss: 0.0201 Epoch 6/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 93ms/step - loss: 0.0214 - val_loss: 0.0187 Epoch 7/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 97ms/step - loss: 0.0198 - val_loss: 0.0171 Epoch 8/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 89ms/step - loss: 0.0186 - val_loss: 0.0162 Epoch 9/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 89ms/step - loss: 0.0180 - val_loss: 0.0161 Epoch 10/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 102ms/step - loss: 0.0176 - val_loss: 0.0164 Epoch 11/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 89ms/step - loss: 0.0171 - val_loss: 0.0156 Epoch 12/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 89ms/step - loss: 0.0168 - val_loss: 0.0159 Epoch 13/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 106ms/step - loss: 0.0169 - val_loss: 0.0157 Epoch 14/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 93ms/step - loss: 0.0163 - val_loss: 0.0154 Epoch 15/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 94ms/step - loss: 0.0163 - val_loss: 0.0152 Epoch 16/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 107ms/step - loss: 0.0160 - val_loss: 0.0154 Epoch 17/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 89ms/step - loss: 0.0159 - val_loss: 0.0150 Epoch 18/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 89ms/step - loss: 0.0157 - val_loss: 0.0152 Epoch 19/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 94ms/step - loss: 0.0154 - val_loss: 0.0149 Epoch 20/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 95ms/step - loss: 0.0153 - val_loss: 0.0149 Epoch 21/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 89ms/step - loss: 0.0153 - val_loss: 0.0149 Epoch 22/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 88ms/step - loss: 0.0152 - val_loss: 0.0150 Epoch 23/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 103ms/step - loss: 0.0153 - val_loss: 0.0150
# Training and overfitting tracking
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3))
_ = forecaster.plot_history(ax=ax)
# Prediction
# ==============================================================================
predictions = forecaster.predict()
predictions.head(4)
| level | pred | |
|---|---|---|
| 2021-04-01 00:00:00 | o3 | 58.227726 |
| 2021-04-01 01:00:00 | o3 | 48.631939 |
| 2021-04-01 02:00:00 | o3 | 43.005013 |
| 2021-04-01 03:00:00 | o3 | 37.624439 |
# Backtesting with test data
# ==============================================================================
cv = TimeSeriesFold(
steps = forecaster.max_step,
initial_train_size = len(data.loc[:end_validation, :]), # Training + Validation Data
refit = False
)
# The validation partition is now used as part of the initial fit
# Epocs is set to the value idenfied in the previous training with early stopping
forecaster.set_fit_kwargs({"epochs": 20,"batch_size": 512})
metrics, predictions = backtesting_forecaster_multiseries(
forecaster = forecaster,
series = data,
cv = cv,
levels = forecaster.levels,
metric = "mean_absolute_error",
suppress_warnings = True,
verbose = False
)
Using 'torch' backend with device: cuda Epoch 1/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 79ms/step - loss: 0.0153 Epoch 2/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 90ms/step - loss: 0.0151 Epoch 3/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 81ms/step - loss: 0.0149 Epoch 4/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 78ms/step - loss: 0.0148 Epoch 5/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 87ms/step - loss: 0.0146 Epoch 6/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 90ms/step - loss: 0.0147 Epoch 7/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 79ms/step - loss: 0.0147 Epoch 8/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 86ms/step - loss: 0.0145 Epoch 9/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 80ms/step - loss: 0.0144 Epoch 10/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 80ms/step - loss: 0.0145 Epoch 11/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 85ms/step - loss: 0.0142 Epoch 12/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 83ms/step - loss: 0.0141 Epoch 13/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 79ms/step - loss: 0.0142 Epoch 14/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 85ms/step - loss: 0.0139 Epoch 15/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 88ms/step - loss: 0.0137 Epoch 16/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 81ms/step - loss: 0.0138 Epoch 17/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 89ms/step - loss: 0.0136 Epoch 18/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 86ms/step - loss: 0.0136 Epoch 19/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 79ms/step - loss: 0.0136 Epoch 20/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 86ms/step - loss: 0.0133
0%| | 0/92 [00:00<?, ?it/s]
# Backtesting metrics
# ==============================================================================
metric_multivariate = metrics.loc[metrics["levels"] == "o3", "mean_absolute_error"].iat[0]
metrics
| levels | mean_absolute_error | |
|---|---|---|
| 0 | o3 | 11.017365 |
# Backtesting predictions
# ==============================================================================
predictions
| level | fold | pred | |
|---|---|---|---|
| 2021-10-01 00:00:00 | o3 | 0 | 51.076584 |
| 2021-10-01 01:00:00 | o3 | 0 | 45.454769 |
| 2021-10-01 02:00:00 | o3 | 0 | 40.230427 |
| 2021-10-01 03:00:00 | o3 | 0 | 37.125874 |
| 2021-10-01 04:00:00 | o3 | 0 | 31.917921 |
| ... | ... | ... | ... |
| 2021-12-31 19:00:00 | o3 | 91 | 23.819025 |
| 2021-12-31 20:00:00 | o3 | 91 | 19.483900 |
| 2021-12-31 21:00:00 | o3 | 91 | 20.486601 |
| 2021-12-31 22:00:00 | o3 | 91 | 21.828110 |
| 2021-12-31 23:00:00 | o3 | 91 | 21.231228 |
2208 rows × 3 columns
# % Error vs series mean
# ==============================================================================
rel_mse = 100 * metrics.loc[0, 'mean_absolute_error'] / np.mean(data["o3"])
print(f"Serie mean: {np.mean(data['o3']):0.2f}")
print(f"Relative error (mae): {rel_mse:0.2f} %")
Serie mean: 54.52 Relative error (mae): 20.21 %
# Plotting predictions vs real values in the test set
# ==============================================================================
fig = go.Figure()
trace1 = go.Scatter(x=data_test.index, y=data_test['o3'], name="test", mode="lines")
trace2 = go.Scatter(
x=predictions.index,
y=predictions.loc[predictions["level"] == "o3", "pred"],
name="predictions", mode="lines"
)
fig.add_trace(trace1)
fig.add_trace(trace2)
fig.update_layout(
title="Prediction vs real values in the test set",
xaxis_title="Date time",
yaxis_title="O3",
width=800,
height=400,
margin=dict(l=20, r=20, t=35, b=20),
legend=dict(orientation="h", yanchor="top", y=1.05, xanchor="left", x=0)
)
fig.show()
When using multiple time series as predictors, it is often expected that the model will produce more accurate forecasts for the target series. However, in some cases, the predictions are actually worse than in the previous case where only a single series was used as input. This may happen if the additional time series used as predictors are not strongly related to the target series. As a result, the model is unable to learn meaningful relationships, and the extra information does not improve performance, in fact, it may even introduce noise.
N:M Problems — Multi-series, multi-output¶
In this scenario, the goal is to predict multiple future values for several time series at once, using the historical data from all available series as input. This is known as multivariate-multioutput forecasting.
With this approach, a single model learns to predict several target series simultaneously, capturing relationships and dependencies not only within each series, but also across different series.
Real-world applications include:
Forecasting the sales of multiple products in an online store, leveraging past sales, pricing history, promotions, and other product-related variables.
Study the flue gas emissions of a gas turbine, where you want to predict the concentration of multiple pollutants (e.g., NOX, CO) based on past emissions data and other related variables.
Modeling environmental variables (e.g., pollution, temperature, humidity) together, where the evolution of one variable may influence or be influenced by others.
# Create model
# ==============================================================================
levels = ['o3', 'pm2.5', 'pm10'] # Multiple target series to predict
lags = 24
model = create_and_compile_model(
series = data, # DataFrame with all series (predictors)
levels = levels,
lags = lags,
steps = 24,
recurrent_layer = "LSTM",
recurrent_units = [128, 64],
recurrent_layers_kwargs = {"activation": "tanh"},
dense_units = [64, 32],
compile_kwargs = {'optimizer': Adam(), 'loss': MeanSquaredError()},
model_name = "MultiVariate-MultiOutput-Multi-Step"
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "MultiVariate-MultiOutput-Multi-Step"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 24, 10) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ lstm_1 (LSTM) │ (None, 24, 128) │ 71,168 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ lstm_2 (LSTM) │ (None, 64) │ 49,408 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 64) │ 4,160 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_2 (Dense) │ (None, 32) │ 2,080 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 72) │ 2,376 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 24, 3) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 129,192 (504.66 KB)
Trainable params: 129,192 (504.66 KB)
Non-trainable params: 0 (0.00 B)
# Forecaster Creation
# ==============================================================================
forecaster = ForecasterRnn(
estimator=model,
levels=levels,
lags=lags,
transformer_series=MinMaxScaler(),
fit_kwargs={
"epochs": 25,
"batch_size": 512,
"callbacks": [
EarlyStopping(monitor="val_loss", patience=3, restore_best_weights=True)
], # Callback to stop training when it is no longer learning.
"series_val": data_val, # Validation data for model training.
},
)
# Fit forecaster
# ==============================================================================
forecaster.fit(data_train)
Using 'torch' backend with device: cuda Epoch 1/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 79ms/step - loss: 0.0500 - val_loss: 0.0197 Epoch 2/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 79ms/step - loss: 0.0162 - val_loss: 0.0103 Epoch 3/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 95ms/step - loss: 0.0120 - val_loss: 0.0101 Epoch 4/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 78ms/step - loss: 0.0111 - val_loss: 0.0092 Epoch 5/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 79ms/step - loss: 0.0105 - val_loss: 0.0086 Epoch 6/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 89ms/step - loss: 0.0097 - val_loss: 0.0073 Epoch 7/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 84ms/step - loss: 0.0088 - val_loss: 0.0067 Epoch 8/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 78ms/step - loss: 0.0083 - val_loss: 0.0063 Epoch 9/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 81ms/step - loss: 0.0080 - val_loss: 0.0062 Epoch 10/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 94ms/step - loss: 0.0078 - val_loss: 0.0061 Epoch 11/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 78ms/step - loss: 0.0076 - val_loss: 0.0065 Epoch 12/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 79ms/step - loss: 0.0075 - val_loss: 0.0062 Epoch 13/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 91ms/step - loss: 0.0075 - val_loss: 0.0060 Epoch 14/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 90ms/step - loss: 0.0073 - val_loss: 0.0059 Epoch 15/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 80ms/step - loss: 0.0071 - val_loss: 0.0058 Epoch 16/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 83ms/step - loss: 0.0069 - val_loss: 0.0059 Epoch 17/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 94ms/step - loss: 0.0069 - val_loss: 0.0057 Epoch 18/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 79ms/step - loss: 0.0069 - val_loss: 0.0060 Epoch 19/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 79ms/step - loss: 0.0067 - val_loss: 0.0056 Epoch 20/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 79ms/step - loss: 0.0066 - val_loss: 0.0057 Epoch 21/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 4s 95ms/step - loss: 0.0066 - val_loss: 0.0058 Epoch 22/25 39/39 ━━━━━━━━━━━━━━━━━━━━ 3s 78ms/step - loss: 0.0065 - val_loss: 0.0057
# Training and overfitting tracking
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3))
_ = forecaster.plot_history(ax=ax)
Predictions can be made for specific steps and levels as long as they are within the prediction horizon defined by the model. For example, you can predict ozone concentration (levels = "o3") for the next one and five hours (steps = [1, 5]).
# Specific steps and levels predictions
# ==============================================================================
forecaster.predict(steps=[1, 5], levels="o3")
| level | pred | |
|---|---|---|
| 2021-04-01 00:00:00 | o3 | 51.614090 |
| 2021-04-01 04:00:00 | o3 | 35.231655 |
# Predictions for all steps and levels
# ==============================================================================
predictions = forecaster.predict()
predictions
| level | pred | |
|---|---|---|
| 2021-04-01 00:00:00 | o3 | 51.614090 |
| 2021-04-01 00:00:00 | pm2.5 | 15.563469 |
| 2021-04-01 00:00:00 | pm10 | 19.594376 |
| 2021-04-01 01:00:00 | o3 | 46.534138 |
| 2021-04-01 01:00:00 | pm2.5 | 15.019449 |
| ... | ... | ... |
| 2021-04-01 22:00:00 | pm2.5 | 12.719211 |
| 2021-04-01 22:00:00 | pm10 | 17.417959 |
| 2021-04-01 23:00:00 | o3 | 56.436928 |
| 2021-04-01 23:00:00 | pm2.5 | 13.698158 |
| 2021-04-01 23:00:00 | pm10 | 20.107550 |
72 rows × 2 columns
# Backtesting with test data
# ==============================================================================
cv = TimeSeriesFold(
steps = forecaster.max_step,
initial_train_size = len(data.loc[:end_validation, :]), # Training + Validation Data
refit = False
)
# The validation partition is now used as part of the initial fit
# Epocs is set to the value idenfied in the previous training with early stopping
forecaster.set_fit_kwargs({"epochs": 20,"batch_size": 512})
metrics, predictions = backtesting_forecaster_multiseries(
forecaster = forecaster,
series = data,
cv = cv,
levels = forecaster.levels,
metric = "mean_absolute_error",
suppress_warnings = True,
verbose = False
)
Using 'torch' backend with device: cuda Epoch 1/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 69ms/step - loss: 0.0064 Epoch 2/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 83ms/step - loss: 0.0063 Epoch 3/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 69ms/step - loss: 0.0063 Epoch 4/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 70ms/step - loss: 0.0062 Epoch 5/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 81ms/step - loss: 0.0061 Epoch 6/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 69ms/step - loss: 0.0061 Epoch 7/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 69ms/step - loss: 0.0060 Epoch 8/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 70ms/step - loss: 0.0059 Epoch 9/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 80ms/step - loss: 0.0059 Epoch 10/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 69ms/step - loss: 0.0059 Epoch 11/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 69ms/step - loss: 0.0058 Epoch 12/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 81ms/step - loss: 0.0058 Epoch 13/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 69ms/step - loss: 0.0056 Epoch 14/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 70ms/step - loss: 0.0056 Epoch 15/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 71ms/step - loss: 0.0055 Epoch 16/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 80ms/step - loss: 0.0054 Epoch 17/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 70ms/step - loss: 0.0054 Epoch 18/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 69ms/step - loss: 0.0053 Epoch 19/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 4s 81ms/step - loss: 0.0052 Epoch 20/20 47/47 ━━━━━━━━━━━━━━━━━━━━ 3s 69ms/step - loss: 0.0052
0%| | 0/92 [00:00<?, ?it/s]
# Backtesting metrics
# ==============================================================================
metric_multivariate_multioutput = metrics.loc[metrics["levels"] == "o3", "mean_absolute_error"].iat[0]
metrics
| levels | mean_absolute_error | |
|---|---|---|
| 0 | o3 | 12.011655 |
| 1 | pm2.5 | 4.264126 |
| 2 | pm10 | 12.057429 |
| 3 | average | 9.444403 |
| 4 | weighted_average | 9.444403 |
| 5 | pooling | 9.444403 |
# Plotting predictions vs real values in the test set
# =============================================================================
for i, level in enumerate(levels):
fig = go.Figure()
trace1 = go.Scatter(x=data_test.index, y=data_test[level], name="test", mode="lines")
trace2 = go.Scatter(
x=predictions.loc[predictions["level"] == level, "pred"].index,
y=predictions.loc[predictions["level"] == level, "pred"],
name="predictions", mode="lines"
)
fig.add_trace(trace1)
fig.add_trace(trace2)
fig.update_layout(
title="Prediction vs real values in the test set",
xaxis_title="Date time",
yaxis_title=level,
width=800,
height=300,
margin=dict(l=20, r=20, t=35, b=20),
legend=dict(orientation="h", yanchor="top", y=1.05, xanchor="left", x=0)
)
fig.show()
O3: The model tracks the main trend and seasonal patterns, but smooths out some of the more extreme peaks and valleys.
pm2.5: Predictions follow the overall changes, but the model misses some of the sudden spikes.
pm10: The model captures general trends but consistently underestimates larger peaks and rapid jumps.
The model reproduces the main behavior of each series, but tends to miss or smooth out sharp fluctuations.
Comparing Forecasting Strategies¶
As we have seen, various deep learning architectures and modeling strategies can be employed for time series forecasting. In summary, the forecasting approaches can be categorized into:
Single series, multi-step forecasting: Predict future values of a single series using only its past values.
Multivariate, single-output, multi-step forecasting: Use several series as predictors to forecast a target series over multiple future time steps.
Multivariate, multi-output, multi-step forecasting: Use multiple predictor series to forecast several targets over multiple steps.
Below is a summary table comparing the Mean Absolute Error (MAE) for each approach, calculated on the same target series, "o3":
# Metric comparison
# ==============================================================================
results = {
"Single-Series, Multi-Step": metric_single_series,
"Multi-Series, Single-Output": metric_multivariate,
"Multi-Series, Multi-Output": metric_multivariate_multioutput
}
table_results = pd.DataFrame.from_dict(results, orient='index', columns=['O3 MAE'])
table_results = table_results.style.highlight_min(axis=0, color='green').format(precision=4)
table_results
| O3 MAE | |
|---|---|
| Single-Series, Multi-Step | 11.0111 |
| Multi-Series, Single-Output | 11.0174 |
| Multi-Series, Multi-Output | 12.0117 |
In this example, the single-series and simple multivariate approaches produce similar errors, while adding more targets as outputs (multi-output) increases the prediction error. However, there is no universal rule: the best strategy depends on your data, domain, and prediction goals.
It's important to experiment with different architectures and compare their metrics to select the most appropriate model for your specific use case.
Exogenous variables in deep learning models¶
Exogenous variables are external predictors (such as weather, holidays, or special events) that can influence the target series but are not part of its own historical values. When building deep learning models for time series forecasting, including these variables can help capture important patterns and improve accuracy, as long as their future values are available at prediction time.
In this section, we’ll demonstrate how to use exogenous variables in deep learning models with a new dataset: bike_sharing, which contains hourly bike usage in Washington D.C., together with weather and holiday information.
To learn more about exogenous variables in skforecast visit the exogenous variables user guide.
# Data download
# ==============================================================================
data_exog = fetch_dataset(name='bike_sharing', raw=False)
data_exog = data_exog[['users', 'temp', 'hum', 'windspeed', 'holiday']]
data_exog = data_exog.loc['2011-04-01 00:00:00':'2012-10-20 23:00:00', :].copy()
data_exog.head(3)
╭───────────────────────────────── bike_sharing ──────────────────────────────────╮ │ Description: │ │ Hourly usage of the bike share system in the city of Washington D.C. during the │ │ years 2011 and 2012. In addition to the number of users per hour, information │ │ about weather conditions and holidays is available. │ │ │ │ Source: │ │ Fanaee-T,Hadi. (2013). Bike Sharing Dataset. UCI Machine Learning Repository. │ │ https://doi.org/10.24432/C5W894. │ │ │ │ URL: │ │ https://raw.githubusercontent.com/skforecast/skforecast- │ │ datasets/main/data/bike_sharing_dataset_clean.csv │ │ │ │ Shape: 17544 rows x 11 columns │ ╰─────────────────────────────────────────────────────────────────────────────────╯
| users | temp | hum | windspeed | holiday | |
|---|---|---|---|---|---|
| date_time | |||||
| 2011-04-01 00:00:00 | 6.0 | 10.66 | 100.0 | 11.0014 | 0.0 |
| 2011-04-01 01:00:00 | 4.0 | 10.66 | 100.0 | 11.0014 | 0.0 |
| 2011-04-01 02:00:00 | 7.0 | 10.66 | 93.0 | 12.9980 | 0.0 |
# Calendar features
# ==============================================================================
features_to_extract = [
'month',
'week',
'day_of_week',
'hour'
]
calendar_transformer = DatetimeFeatures(
variables = 'index',
features_to_extract = features_to_extract,
drop_original = False,
)
# Cyclical encoding of calendar features
# ==============================================================================
features_to_encode = [
"month",
"week",
"day_of_week",
"hour",
]
max_values = {
"month": 12,
"week": 52,
"day_of_week": 7,
"hour": 24,
}
cyclical_encoder = CyclicalFeatures(
variables = features_to_encode,
max_values = max_values,
drop_original = True
)
exog_transformer = make_pipeline(
calendar_transformer,
cyclical_encoder
)
data_exog = exog_transformer.fit_transform(data_exog)
exog_features = data_exog.columns.difference(['users']).tolist()
print(f"Exogenous features: {exog_features}")
data_exog.head(3)
Exogenous features: ['day_of_week_cos', 'day_of_week_sin', 'holiday', 'hour_cos', 'hour_sin', 'hum', 'month_cos', 'month_sin', 'temp', 'week_cos', 'week_sin', 'windspeed']
| users | temp | hum | windspeed | holiday | month_sin | month_cos | week_sin | week_cos | day_of_week_sin | day_of_week_cos | hour_sin | hour_cos | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| date_time | |||||||||||||
| 2011-04-01 00:00:00 | 6.0 | 10.66 | 100.0 | 11.0014 | 0.0 | 0.866025 | -0.5 | 1.0 | 6.123234e-17 | -0.433884 | -0.900969 | 0.000000 | 1.000000 |
| 2011-04-01 01:00:00 | 4.0 | 10.66 | 100.0 | 11.0014 | 0.0 | 0.866025 | -0.5 | 1.0 | 6.123234e-17 | -0.433884 | -0.900969 | 0.258819 | 0.965926 |
| 2011-04-01 02:00:00 | 7.0 | 10.66 | 93.0 | 12.9980 | 0.0 | 0.866025 | -0.5 | 1.0 | 6.123234e-17 | -0.433884 | -0.900969 | 0.500000 | 0.866025 |
# Split train-validation-test
# ==============================================================================
end_train = '2012-06-30 23:59:00'
end_validation = '2012-10-01 23:59:00'
data_exog_train = data_exog.loc[: end_train, :]
data_exog_val = data_exog.loc[end_train:end_validation, :]
data_exog_test = data_exog.loc[end_validation:, :]
print(f"Dates train : {data_exog_train.index.min()} --- {data_exog_train.index.max()} (n={len(data_exog_train)})")
print(f"Dates validation : {data_exog_val.index.min()} --- {data_exog_val.index.max()} (n={len(data_exog_val)})")
print(f"Dates test : {data_exog_test.index.min()} --- {data_exog_test.index.max()} (n={len(data_exog_test)})")
Dates train : 2011-04-01 00:00:00 --- 2012-06-30 23:00:00 (n=10968) Dates validation : 2012-07-01 00:00:00 --- 2012-10-01 23:00:00 (n=2232) Dates test : 2012-10-02 00:00:00 --- 2012-10-20 23:00:00 (n=456)
The architecture of your deep learning model must be able to accept extra inputs alongside the main time series data. The create_and_compile_model function makes this straightforward: simply pass the exogenous variables as a DataFrame to the exog argument.
# `create_and_compile_model` with exogenous variables
# ==============================================================================
series = ['users']
levels = ['users']
lags = 72
model = create_and_compile_model(
series = data_exog[series], # Single-series
levels = levels, # One target series to predict
lags = lags,
steps = 36,
exog = data_exog[exog_features], # Exogenous variables
recurrent_layer = "LSTM",
recurrent_units = [128, 64],
recurrent_layers_kwargs = {"activation": "tanh"},
dense_units = [64, 32],
compile_kwargs = {'optimizer': Adam(learning_rate=0.01), 'loss': 'mse'},
model_name = "Single-Series-Multi-Step-Exog"
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "Single-Series-Multi-Step-Exog"
┏━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ Connected to ┃ ┡━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━┩ │ series_input │ (None, 72, 1) │ 0 │ - │ │ (InputLayer) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ lstm_1 (LSTM) │ (None, 72, 128) │ 66,560 │ series_input[0][… │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ lstm_2 (LSTM) │ (None, 64) │ 49,408 │ lstm_1[0][0] │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ repeat_vector │ (None, 36, 64) │ 0 │ lstm_2[0][0] │ │ (RepeatVector) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ exog_input │ (None, 36, 12) │ 0 │ - │ │ (InputLayer) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ concat_exog │ (None, 36, 76) │ 0 │ repeat_vector[0]… │ │ (Concatenate) │ │ │ exog_input[0][0] │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ dense_td_1 │ (None, 36, 64) │ 4,928 │ concat_exog[0][0] │ │ (TimeDistributed) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ dense_td_2 │ (None, 36, 32) │ 2,080 │ dense_td_1[0][0] │ │ (TimeDistributed) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ output_dense_td_la… │ (None, 36, 1) │ 33 │ dense_td_2[0][0] │ │ (TimeDistributed) │ │ │ │ └─────────────────────┴───────────────────┴────────────┴───────────────────┘
Total params: 123,009 (480.50 KB)
Trainable params: 123,009 (480.50 KB)
Non-trainable params: 0 (0.00 B)
# Plotting the model architecture (require `pydot` and `graphviz`)
# ==============================================================================
# from keras.utils import plot_model
# plot_model(model, show_shapes=True, show_layer_names=True, to_file='model-architecture-exog.png')

# Forecaster Creation
# ==============================================================================
forecaster = ForecasterRnn(
estimator=model,
levels=levels,
lags=lags,
transformer_series=MinMaxScaler(),
transformer_exog=MinMaxScaler(),
fit_kwargs={
"epochs": 25,
"batch_size": 1024,
"callbacks": [
EarlyStopping(monitor="val_loss", patience=3, restore_best_weights=True),
ReduceLROnPlateau(monitor="val_loss", factor=0.5, patience=2, min_lr=1e-5, verbose=1)
], # Callback to stop training when it is no longer learning and to reduce learning rate.
"series_val": data_exog_val[series], # Validation data for model training.
"exog_val": data_exog_val[exog_features] # Validation data for exogenous variables
},
)
# Fit forecaster with exogenous variables
# ==============================================================================
forecaster.fit(
series = data_exog_train[series],
exog = data_exog_train[exog_features]
)
Using 'torch' backend with device: cuda Epoch 1/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 4s 343ms/step - loss: 0.0954 - val_loss: 0.0720 - learning_rate: 0.0100 Epoch 2/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 259ms/step - loss: 0.0215 - val_loss: 0.0394 - learning_rate: 0.0100 Epoch 3/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 251ms/step - loss: 0.0157 - val_loss: 0.0340 - learning_rate: 0.0100 Epoch 4/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 254ms/step - loss: 0.0141 - val_loss: 0.0328 - learning_rate: 0.0100 Epoch 5/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 310ms/step - loss: 0.0135 - val_loss: 0.0329 - learning_rate: 0.0100 Epoch 6/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 254ms/step - loss: 0.0122 - val_loss: 0.0298 - learning_rate: 0.0100 Epoch 7/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 254ms/step - loss: 0.0110 - val_loss: 0.0313 - learning_rate: 0.0100 Epoch 8/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 218ms/step - loss: 0.0104 Epoch 8: ReduceLROnPlateau reducing learning rate to 0.004999999888241291. 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 259ms/step - loss: 0.0104 - val_loss: 0.0324 - learning_rate: 0.0100 Epoch 9/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 316ms/step - loss: 0.0099 - val_loss: 0.0299 - learning_rate: 0.0050
# Training and overfitting tracking
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3))
_ = forecaster.plot_history(ax=ax)
The training history shows that while the training loss decreases smoothly, the validation loss stays higher and fluctuates across epochs. This suggests that the model is likely overfitting: it learns the training data well but struggles to generalize to new, unseen data. To address this, you could try adding regularization such as dropout, simplifying the model by reducing its size, or revisiting the choice of exogenous features to help improve validation performance.
When using exogenous variables, the predict requires additional information about the future values of these variables. This data must be provided through the exog argument in the predict method.
# Prediction with exogenous variables
# ==============================================================================
predictions = forecaster.predict(exog=data_exog_val[exog_features])
predictions.head(4)
| level | pred | |
|---|---|---|
| 2012-07-01 00:00:00 | users | 98.951996 |
| 2012-07-01 01:00:00 | users | 63.853760 |
| 2012-07-01 02:00:00 | users | 40.953781 |
| 2012-07-01 03:00:00 | users | 24.105370 |
# Backtesting with test data and exogenous variables
# ==============================================================================
cv = TimeSeriesFold(
steps = forecaster.max_step,
initial_train_size = len(data_exog.loc[:end_validation, :]), # Training + Validation Data
refit = False
)
# The validation partition is now used as part of the initial fit
# Epocs is set to the value idenfied in the previous training with early stopping
forecaster.set_fit_kwargs({"epochs": 21,"batch_size": 1024})
metrics, predictions = backtesting_forecaster_multiseries(
forecaster = forecaster,
series = data_exog[series],
exog = data_exog[exog_features],
cv = cv,
levels = forecaster.levels,
metric = "mean_absolute_error",
suppress_warnings = True,
verbose = False
)
Using 'torch' backend with device: cuda Epoch 1/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 216ms/step - loss: 0.0133 Epoch 2/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 219ms/step - loss: 0.0122 Epoch 3/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 268ms/step - loss: 0.0113 Epoch 4/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 217ms/step - loss: 0.0108 Epoch 5/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 219ms/step - loss: 0.0103 Epoch 6/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 214ms/step - loss: 0.0098 Epoch 7/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 267ms/step - loss: 0.0090 Epoch 8/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 216ms/step - loss: 0.0084 Epoch 9/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 216ms/step - loss: 0.0078 Epoch 10/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 220ms/step - loss: 0.0072 Epoch 11/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 263ms/step - loss: 0.0069 Epoch 12/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 217ms/step - loss: 0.0064 Epoch 13/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 219ms/step - loss: 0.0061 Epoch 14/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 216ms/step - loss: 0.0058 Epoch 15/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 266ms/step - loss: 0.0057 Epoch 16/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 215ms/step - loss: 0.0055 Epoch 17/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 217ms/step - loss: 0.0055 Epoch 18/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 216ms/step - loss: 0.0050 Epoch 19/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 268ms/step - loss: 0.0049 Epoch 20/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 215ms/step - loss: 0.0047 Epoch 21/21 13/13 ━━━━━━━━━━━━━━━━━━━━ 3s 216ms/step - loss: 0.0046
0%| | 0/13 [00:00<?, ?it/s]
# Backtesting metrics
# ==============================================================================
metrics
| levels | mean_absolute_error | |
|---|---|---|
| 0 | users | 64.344754 |
# Plotting predictions vs real values in the test set
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3))
data_exog_test["users"].plot(ax=ax, label="test")
predictions.loc[predictions["level"] == "users", "pred"].plot(ax=ax, label="predictions")
ax.set_title("users")
ax.legend();
Probabilistic forecasting with deep learning models¶
Conformal prediction is a framework for constructing prediction intervals that are guaranteed to contain the true value with a specified probability (coverage probability). It works by combining the predictions of a point-forecasting model with its past residuals, differences between previous predictions and actual values. These residuals help estimate the uncertainty in the forecast and determine the width of the prediction interval that is then added to the point forecast.
To learn more about conformal predictions in skforecast, visit the Probabilistic Forecasting: Conformal Prediction user guide.
# Store in-sample residuals
# ==============================================================================
forecaster.set_in_sample_residuals(
series=data_exog_train[series], exog=data_exog_train[exog_features]
)
# Prediction intervals
# ==============================================================================
predictions = forecaster.predict_interval(
steps = None,
exog = data_exog_val.loc[:, exog_features],
interval = [10, 90], # 80% prediction interval
method = 'conformal',
use_in_sample_residuals = True
)
predictions.head(4)
| level | pred | lower_bound | upper_bound | |
|---|---|---|---|---|
| 2012-07-01 00:00:00 | users | 98.951999 | -15.838422 | 213.742420 |
| 2012-07-01 01:00:00 | users | 63.853762 | -50.936659 | 178.644183 |
| 2012-07-01 02:00:00 | users | 40.953780 | -73.836641 | 155.744201 |
| 2012-07-01 03:00:00 | users | 24.105370 | -90.685051 | 138.895791 |
# Plot intervals
# ==============================================================================
plot_prediction_intervals(
predictions = predictions,
y_true = data_exog_val,
target_variable = "users",
title = "Predicted intervals",
kwargs_fill_between = {'color': 'gray', 'alpha': 0.4, 'zorder': 1}
)
Using Custom Loss Functions in Deep Learning Models¶
By default, Keras models in skforecast can be trained using common loss functions such as MeanSquaredError or MeanAbsoluteError. However, in many forecasting tasks it is useful to design a custom loss function that reflects the specific goals of your problem. For example, you may want to penalize underestimation more than overestimation, handle imbalanced data, or directly optimize for a business-specific metric.
Keras and skforecast make this process straightforward:
You can define a loss as a Python function that takes
y_trueandy_predtensors and returns a scalar loss value.For reproducibility and model saving/loading, custom losses should be registered with
@keras.saving.register_keras_serializable().
This flexibility enables you to customize the training process according to your forecasting domain, ensuring that the model optimizes the metrics that are most relevant to your use case.
# Create custom loss function with tensorflow
# ==============================================================================
# import tensorflow as tf
# @keras.saving.register_keras_serializable(package="custom", name="weighted_mae")
# def weighted_mae(y_true, y_pred):
# error = tf.abs(y_true - y_pred)
# weights = tf.abs(y_true)
# return tf.reduce_mean(error * weights)
# Create custom loss function with pytorch
# ==============================================================================
@keras.saving.register_keras_serializable(package="custom", name="weighted_mae")
def weighted_mae(y_true, y_pred):
"""
Compute weighted mean absolute error.
Args:
y_true (torch.Tensor): Ground truth values.
y_pred (torch.Tensor): Predicted values.
Returns:
torch.Tensor: Weighted MAE loss (scalar).
"""
error = torch.abs(y_true - y_pred)
weights = torch.abs(y_true)
return torch.mean(error * weights)
# `create_and_compile_model` with custom loss function
# ==============================================================================
series = ['users']
levels = ['users']
lags = 72
model = create_and_compile_model(
series = data_exog[series],
levels = levels,
lags = lags,
steps = 36,
exog = data_exog[exog_features],
recurrent_layer = "LSTM",
recurrent_units = [128, 64],
recurrent_layers_kwargs = {"activation": "tanh"},
dense_units = [64, 32],
compile_kwargs = {'optimizer': Adam(learning_rate=0.01), 'loss': weighted_mae}, # Custom loss function
model_name = "Single-Series-Multi-Step-Exog"
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "Single-Series-Multi-Step-Exog"
┏━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ Connected to ┃ ┡━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━┩ │ series_input │ (None, 72, 1) │ 0 │ - │ │ (InputLayer) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ lstm_1 (LSTM) │ (None, 72, 128) │ 66,560 │ series_input[0][… │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ lstm_2 (LSTM) │ (None, 64) │ 49,408 │ lstm_1[0][0] │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ repeat_vector │ (None, 36, 64) │ 0 │ lstm_2[0][0] │ │ (RepeatVector) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ exog_input │ (None, 36, 12) │ 0 │ - │ │ (InputLayer) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ concat_exog │ (None, 36, 76) │ 0 │ repeat_vector[0]… │ │ (Concatenate) │ │ │ exog_input[0][0] │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ dense_td_1 │ (None, 36, 64) │ 4,928 │ concat_exog[0][0] │ │ (TimeDistributed) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ dense_td_2 │ (None, 36, 32) │ 2,080 │ dense_td_1[0][0] │ │ (TimeDistributed) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ output_dense_td_la… │ (None, 36, 1) │ 33 │ dense_td_2[0][0] │ │ (TimeDistributed) │ │ │ │ └─────────────────────┴───────────────────┴────────────┴───────────────────┘
Total params: 123,009 (480.50 KB)
Trainable params: 123,009 (480.50 KB)
Non-trainable params: 0 (0.00 B)
# Forecaster Creation
# ==============================================================================
forecaster = ForecasterRnn(
estimator=model,
levels=levels,
lags=lags,
transformer_series=MinMaxScaler(),
transformer_exog=MinMaxScaler(),
fit_kwargs={
"epochs": 25,
"batch_size": 1024,
"callbacks": [
EarlyStopping(monitor="val_loss", patience=3, restore_best_weights=True),
ReduceLROnPlateau(monitor="val_loss", factor=0.5, patience=2, min_lr=1e-5, verbose=1)
], # Callback to stop training when it is no longer learning and to reduce learning rate.
"series_val": data_exog_val[series], # Validation data for model training.
"exog_val": data_exog_val[exog_features] # Validation data for exogenous variables
},
)
# Fit forecaster with exogenous variables
# ==============================================================================
forecaster.fit(
series = data_exog_train[series],
exog = data_exog_train[exog_features]
)
Using 'torch' backend with device: cuda Epoch 1/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 4s 328ms/step - loss: 0.0515 - val_loss: 0.0677 - learning_rate: 0.0100 Epoch 2/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 253ms/step - loss: 0.0266 - val_loss: 0.0569 - learning_rate: 0.0100 Epoch 3/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 257ms/step - loss: 0.0227 - val_loss: 0.0595 - learning_rate: 0.0100 Epoch 4/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 268ms/step - loss: 0.0197 - val_loss: 0.0535 - learning_rate: 0.0100 Epoch 5/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 291ms/step - loss: 0.0180 - val_loss: 0.0506 - learning_rate: 0.0100 Epoch 6/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 253ms/step - loss: 0.0171 - val_loss: 0.0612 - learning_rate: 0.0100 Epoch 7/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 219ms/step - loss: 0.0177 Epoch 7: ReduceLROnPlateau reducing learning rate to 0.004999999888241291. 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 255ms/step - loss: 0.0177 - val_loss: 0.0526 - learning_rate: 0.0100 Epoch 8/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 255ms/step - loss: 0.0159 - val_loss: 0.0488 - learning_rate: 0.0050 Epoch 9/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 299ms/step - loss: 0.0152 - val_loss: 0.0425 - learning_rate: 0.0050 Epoch 10/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 266ms/step - loss: 0.0143 - val_loss: 0.0360 - learning_rate: 0.0050 Epoch 11/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 260ms/step - loss: 0.0136 - val_loss: 0.0420 - learning_rate: 0.0050 Epoch 12/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 217ms/step - loss: 0.0130 Epoch 12: ReduceLROnPlateau reducing learning rate to 0.0024999999441206455. 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 254ms/step - loss: 0.0130 - val_loss: 0.0399 - learning_rate: 0.0050 Epoch 13/25 11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 300ms/step - loss: 0.0122 - val_loss: 0.0378 - learning_rate: 0.0025
# Training and overfitting tracking
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3))
_ = forecaster.plot_history(ax=ax)
# Prediction with exogenous variables
# ==============================================================================
predictions = forecaster.predict(exog=data_exog_val[exog_features])
predictions.head(4)
| level | pred | |
|---|---|---|
| 2012-07-01 00:00:00 | users | 118.054787 |
| 2012-07-01 01:00:00 | users | 100.596344 |
| 2012-07-01 02:00:00 | users | 69.371864 |
| 2012-07-01 03:00:00 | users | 45.221981 |
Understanding create_and_compile_model in depth¶
The create_and_compile_model function is designed to streamline the process of building and compiling RNN-based Keras models for time series forecasting, with or without exogenous variables. This function allows both rapid prototyping (with sensible defaults) and fine-grained customization for advanced users.
How the function works
At its core, create_and_compile_model builds a neural network that consists of three main building blocks:
Recurrent Layers (LSTM, GRU, or SimpleRNN): These layers capture temporal dependencies in the data. You can control the type, number, and configuration of recurrent layers using
recurrent_layer, recurrent_units, andrecurrent_layers_kwargs.Dense (Fully Connected) Layers: After temporal features are extracted, dense layers help model nonlinear relationships between learned features and the forecasting target(s). The structure is controlled by
dense_unitsanddense_layers_kwargs.Output Layer: The final dense layer matches the number of forecasting targets (
levels) and steps (steps). Its configuration can be adjusted withoutput_dense_layer_kwargs.
If you include exogenous variables (exog), the function automatically adjusts the input structure so that the model receives both the main time series and additional features.
Parameters
series: Main time series data (as a DataFrame), each column is treated as an input feature.lags: Number of past time steps to use as predictors. Defines the input sequence length. The same value must be used later in the ForecasterRnnlagsargument.steps: Number of future time steps to predict.levels: List of variables to predict (target variables). Can be one or many columns fromseries. IfNone, defaults to the names of input series.exog: Exogenous variables (optional), given as a DataFrame. Must be aligned withseries.recurrent_layer: Type of recurrent layer, choose between'LSTM','GRU', or'RNN'. Keras API: LSTM, GRU, SimpleRNN.recurrent_units: Number of units per recurrent layer. Accepts a single int (for one layer) or a list/tuple for multiple stacked layers.recurrent_layers_kwargs: Dictionary (same for all layers) or lists of dictionaries (one per layer) with keyword arguments for the respective recurrent layers (e.g., activation functions, dropout, etc.).dense_units: Number of units per dense layer. Accepts a single int (for one layer) or a list/tuple for multiple stacked layers.dense_layers_kwargs: Dictionary (same for all layers) or lists of dictionaries (one per layer) with keyword arguments for the respective dense layers (e.g., activation functions, dropout, etc.).output_dense_layer_kwargs: Dictionary with keyword arguments for the output dense layer (e.g., activation function, dropout, etc.). Defaults to{'activation': 'linear'}.compile_kwargs: Dictionary of parameters for Keras’scompile()method, e.g. optimizer, loss function. Defaults to{'optimizer': Adam(), 'loss': MeanSquaredError()}.model_name: Name of the model.
Visit the full API documentation for create_and_compile_model for more details.
Example: Model summary and layer-by-layer explanation (no exog)¶
# Model summary `create_and_compile_model`
# ==============================================================================
model = create_and_compile_model(
series = data,
levels = ["o3"],
lags = 32,
steps = 24,
recurrent_layer = "GRU",
recurrent_units = 100,
dense_units = 64
)
model.summary()
keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "functional_2"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ series_input (InputLayer) │ (None, 32, 10) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ gru_1 (GRU) │ (None, 100) │ 33,600 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 64) │ 6,464 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output_dense_td_layer (Dense) │ (None, 24) │ 1,560 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 24, 1) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 41,624 (162.59 KB)
Trainable params: 41,624 (162.59 KB)
Non-trainable params: 0 (0.00 B)
| Layer Name | Type | Output Shape | Param # | Description |
|---|---|---|---|---|
| series_input | InputLayer |
(None, 32, 10) |
0 | Input layer of the model. It receives input sequences of length 32 (lags) with 10 features (predictors series) per step. |
| gru_1 | GRU |
(None, 100) |
33,600 | GRU (Gated Recurrent Unit) layer with 100 units and 'tanh' activation. Learns patterns and dependencies over time in the input data. |
| dense_1 | Dense |
(None, 64) |
6,464 | Fully connected (dense) layer with 64 units and ReLU activation. Processes the features extracted by the GRU layer. |
| output_dense_td_layer | Dense |
(None, 24) |
1,560 | Dense output layer with 24 units (one for each of the 24 future time steps to predict), linear activation. |
| reshape | Reshape |
(None, 24, 1) |
0 | Reshapes the output to match the format (steps, output variables). Here, steps=24 and levels=["o3"], so the final output is (None, 24, 1). |
Total params: 41,624 Trainable params: 41,624 Non-trainable params: 0
Example: Model summary and layer-by-layer explanation (exog)¶
# Create calendar exogenous variables
# ==============================================================================
data['hour'] = data.index.hour
data['day_of_week'] = data.index.dayofweek
data = pd.get_dummies(
data, columns=['hour', 'day_of_week'], drop_first=True, dtype=float
)
data.head(3)
| so2 | co | no | no2 | pm10 | nox | o3 | veloc. | direc. | pm2.5 | ... | hour_20 | hour_21 | hour_22 | hour_23 | day_of_week_1 | day_of_week_2 | day_of_week_3 | day_of_week_4 | day_of_week_5 | day_of_week_6 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| datetime | |||||||||||||||||||||
| 2019-01-01 00:00:00 | 8.0 | 0.2 | 3.0 | 36.0 | 22.0 | 40.0 | 16.0 | 0.5 | 262.0 | 19.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2019-01-01 01:00:00 | 8.0 | 0.1 | 2.0 | 40.0 | 32.0 | 44.0 | 6.0 | 0.6 | 248.0 | 26.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2019-01-01 02:00:00 | 8.0 | 0.1 | 11.0 | 42.0 | 36.0 | 58.0 | 3.0 | 0.3 | 224.0 | 31.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
3 rows × 39 columns
# Model summary `create_and_compile_model` with exogenous variables
# ==============================================================================
series = ['so2', 'co', 'no', 'no2', 'pm10', 'nox', 'o3', 'veloc.', 'direc.', 'pm2.5']
exog_features = data.columns.difference(series).tolist() # dayofweek_* and hour_*
levels = ['o3', 'pm2.5', 'pm10'] # Multiple target series to predict
print("Target series:", levels)
print("Series as predictors:", series)
print("Exogenous variables:", exog_features)
print("")
model = create_and_compile_model(
series = data[series],
levels = levels,
lags = 32,
steps = 24,
exog = data[exog_features],
recurrent_layer = "LSTM",
recurrent_units = [128, 64],
recurrent_layers_kwargs = [{'activation': 'tanh'}, {'activation': 'relu'}],
dense_units = [128, 64],
dense_layers_kwargs = {'activation': 'relu'},
output_dense_layer_kwargs = {'activation': 'linear'},
compile_kwargs = {'optimizer': Adam(), 'loss': MeanSquaredError()},
model_name = None
)
model.summary()
Target series: ['o3', 'pm2.5', 'pm10'] Series as predictors: ['so2', 'co', 'no', 'no2', 'pm10', 'nox', 'o3', 'veloc.', 'direc.', 'pm2.5'] Exogenous variables: ['day_of_week_1', 'day_of_week_2', 'day_of_week_3', 'day_of_week_4', 'day_of_week_5', 'day_of_week_6', 'hour_1', 'hour_10', 'hour_11', 'hour_12', 'hour_13', 'hour_14', 'hour_15', 'hour_16', 'hour_17', 'hour_18', 'hour_19', 'hour_2', 'hour_20', 'hour_21', 'hour_22', 'hour_23', 'hour_3', 'hour_4', 'hour_5', 'hour_6', 'hour_7', 'hour_8', 'hour_9'] keras version: 3.10.0 Using backend: torch torch version: 2.9.0+cu126
Model: "functional_3"
┏━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ Connected to ┃ ┡━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━┩ │ series_input │ (None, 32, 10) │ 0 │ - │ │ (InputLayer) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ lstm_1 (LSTM) │ (None, 32, 128) │ 71,168 │ series_input[0][… │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ lstm_2 (LSTM) │ (None, 64) │ 49,408 │ lstm_1[0][0] │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ repeat_vector │ (None, 24, 64) │ 0 │ lstm_2[0][0] │ │ (RepeatVector) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ exog_input │ (None, 24, 29) │ 0 │ - │ │ (InputLayer) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ concat_exog │ (None, 24, 93) │ 0 │ repeat_vector[0]… │ │ (Concatenate) │ │ │ exog_input[0][0] │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ dense_td_1 │ (None, 24, 128) │ 12,032 │ concat_exog[0][0] │ │ (TimeDistributed) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ dense_td_2 │ (None, 24, 64) │ 8,256 │ dense_td_1[0][0] │ │ (TimeDistributed) │ │ │ │ ├─────────────────────┼───────────────────┼────────────┼───────────────────┤ │ output_dense_td_la… │ (None, 24, 3) │ 195 │ dense_td_2[0][0] │ │ (TimeDistributed) │ │ │ │ └─────────────────────┴───────────────────┴────────────┴───────────────────┘
Total params: 141,059 (551.01 KB)
Trainable params: 141,059 (551.01 KB)
Non-trainable params: 0 (0.00 B)
| Layer Name | Type | Output Shape | Param # | Description |
|---|---|---|---|---|
| series_input | InputLayer |
(None, 32, 10) |
0 | Input layer for the main time series. Receives sequences of 32 time steps (lags) for 10 features (predictor series). |
| lstm_1 | LSTM |
(None, 32, 128) |
71,168 | First LSTM layer with 128 units, 'tanh' activation. Learns temporal patterns and dependencies from the input sequences. |
| lstm_2 | LSTM |
(None, 64) |
49,408 | Second LSTM layer with 64 units, 'relu' activation. Further summarizes the temporal information. |
| repeat_vector | RepeatVector |
(None, 24, 64) |
0 | Repeats the output of the previous LSTM layer 24 times, one for each future time step to predict. |
| exog_input | InputLayer |
(None, 24, 29) |
0 | Input layer for the 29 exogenous variables (calendar and hour features) for each of the 24 future time steps. |
| concat_exog | Concatenate |
(None, 24, 93) |
0 | Concatenates the repeated LSTM output and the exogenous variables for each prediction time step, joining all features together. |
| dense_td_1 | TimeDistributed (Dense) |
(None, 24, 128) |
12,032 | Dense layer (128 units, ReLU) applied independently to each of the 24 time steps, learning complex relationships from all features. |
| dense_td_2 | TimeDistributed (Dense) |
(None, 24, 64) |
8,256 | Second dense layer (64 units, ReLU), also applied to each time step, further processes the combined features. |
| output_dense_td_layer | TimeDistributed (Dense) |
(None, 24, 3) |
195 | Final output layer, predicts 3 target variables (levels) for each of the 24 future steps ('linear' activation). |
Total params: 141,059 Trainable params: 141,059 Non-trainable params: 0
Running on GPU¶
skforecast is fully compatible with GPU acceleration. If your computer has a compatible GPU and the right software installed, skforecast will automatically use the GPU to speed up training.
Tips for GPU Training
Batch size matters: Large batch sizes (for example, 64, 128, 256, or even more) allow the GPU to process more data in one go, making training much faster compared to a CPU. Small batch sizes (for example, 8 or 16) don’t use all the power of the GPU, so training may be only a little faster—or sometimes not faster at all—than using just the CPU.
Performance boost: On a suitable GPU, training can be many times faster than on CPU. For example, with a large batch size, an NVIDIA T4 GPU can reduce training time from over a minute (CPU) to just a few seconds (GPU).
How to use the GPU with skforecast
- Install the GPU version of PyTorch (with CUDA support). Visit the PyTorch installation page and follow the instructions for your system. Make sure to select the version that matches your GPU and CUDA version. For example, to install PyTorch with CUDA 12.6, you can run:
pip install torch --index-url https://download.pytorch.org/whl/cu126
- Check if your GPU is available in Python:
# Check if GPU is available
# ==============================================================================
import torch
print("Torch version :", torch.__version__)
print("Cuda available :", torch.cuda.is_available())
print("Device name :", torch.cuda.get_device_name(0) if torch.cuda.is_available() else "CPU")
Torch version : 2.9.0+cu126 Cuda available : True Device name : Tesla T4
- Run your code as usual. If a GPU is detected, skforecast will use it automatically.
How to Extract training and test matrices¶
While forecasting models are mainly used to predict future values, it's just as important to understand how the model is learning from the training data. Analyzing input and output matrices used during training, predictions on the training data or exploring the prediction matrices is crucial for assessing model performance and understanding areas for optimization. This process can reveal whether the model is overfitting, underfitting, or struggling with specific patterns in the data.
To learn about how to extract training and test matrices, visit the How to Extract training and test matrices user guide.
Conclusions¶
Thanks to skforecast, applying deep learning models to time series forecasting is now much more straightforward. The library streamlines everything from data preparation to model selection and evaluation, making it easy to prototype, iterate, and deploy powerful models without needing to write complex custom code. This enables both beginners and experts to experiment with different neural network architectures and quickly identify the best approach for their data and business problem.
Key takeaways from this guide:
Recurrent neural networks (RNNs) are highly flexible: They can be used for a wide range of forecasting tasks, from simple single-series predictions to complex multi-series, multi-output scenarios.
Performance varies with problem complexity: For 1:1 and N:1 setups, the model achieved a lower error, showing strong learning of time series patterns. In N:M cases, the error increases, likely due to higher complexity or less predictable series.
Model selection and architecture matter: Achieving good performance with deep learning requires experimenting with different architectures, which is much easier and faster using skforecast.
Computational demands are significant: Deep learning models can require substantial hardware resources, especially for large datasets or complex architectures.
More series = more context, but not always better individual accuracy: Modeling multiple series together helps capture relationships between them, but may reduce the precision for individual series.
Exogenous variables can boost performance: Including relevant external predictors, like weather or special events, helps models capture real-world influences on the target series.
Session Info¶
import session_info
session_info.show(html=False)
----- feature_engine 1.9.3 keras 3.10.0 matplotlib 3.10.0 numpy 2.0.2 pandas 2.2.2 plotly 5.24.1 session_info v1.0.1 skforecast 0.19.0 sklearn 1.6.1 torch 2.9.0+cu126 ----- IPython 7.34.0 jupyter_client 7.4.9 jupyter_core 5.9.1 notebook 6.5.7 ----- Python 3.12.12 (main, Oct 10 2025, 08:52:57) [GCC 11.4.0] Linux-6.6.105+-x86_64-with-glibc2.35 ----- Session information updated at 2025-11-27 11:46
Citation¶
How to cite this document?
If you use this document or any part of it, we appreciate if you cite it. Thank you very much!
Deep Learning for time series prediction: Recurrent Neural Networks (RNN), Gated Recurrent Unit (GRU), and Long Short-Term Memory (LSTM) by Joaquín Amat Rodrigo, Fernando Carazo and Javier Escobar Ortiz, available under the Attribution-NonCommercial-ShareAlike 4.0 International license at https://www.cienciadedatos.net/documentos/py54-forecasting-con-deep-learning.html
How to cite skforecast
If you use skforecast for a publication, we would appreciate it if you cite the published software.
Zenodo:
Amat Rodrigo, Joaquin, & Escobar Ortiz, Javier. (2025). skforecast (v0.19.0). Zenodo. https://doi.org/10.5281/zenodo.8382788
APA:
Amat Rodrigo, J., & Escobar Ortiz, J. (2025). skforecast (Version 0.19.0) [Computer software]. https://doi.org/10.5281/zenodo.8382788
BibTeX:
@software{skforecast, author = {Amat Rodrigo, Joaquin and Escobar Ortiz, Javier}, title = {skforecast}, version = {0.19.0}, month = {11}, year = {2025}, license = {BSD-3-Clause}, url = {https://skforecast.org/}, doi = {10.5281/zenodo.8382788} }
Did you like the article? Your support is important
Your contribution will help me to continue generating free educational content. Many thanks! 😊
This work by Joaquín Amat Rodrigo, Fernando Carazo and Javier Escobar Ortiz is licensed under a Attribution-NonCommercial-ShareAlike 4.0 International.
Allowed:
-
Share: copy and redistribute the material in any medium or format.
-
Adapt: remix, transform, and build upon the material.
Under the following terms:
-
Attribution: You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
-
NonCommercial: You may not use the material for commercial purposes.
-
ShareAlike: If you remix, transform, or build upon the material, you must distribute your contributions under the same license as the original.


